复杂共形阵列天线宽角域波束扫描设计
张彬超,金 城,田步宁,吕奇皓,曹凯淇,薛正辉
(北京理工大学 集成电路与电子学院,北京 100081)
0 引言
相控阵天线具有增益高、波束扫描快和副瓣水平低等优异性能,因此在雷达和通信系统中受到了广泛关注[1-2]。在卫星通信和远程探测等应用中,相控阵天线往往被要求具有宽角域波束扫描特性。但是,随着波束扫描角的增大,平面相控阵天线的有效辐射孔径将迅速减小,导致增益急剧下降[3]。因此,共形相控阵天线逐渐受到重视,它不仅能良好地兼容不规则的载体平台,还能拓宽波束扫描范围,提高辐射灵活性[4]。
对于共形阵列天线,载体曲率的引入导致阵因子失效,无法通过单元因子和阵因子对阵列方向图进行综合。因此,相比于平面阵列,共形阵列的综合过程更加复杂,且随着载体形状改变而不断变化。为了解决该问题,遗传算法[5-6]、粒子群优化算法[7-8]和杂草入侵优化算法[9-10]等优化算法被用以解决阵列天线的综合问题,且取得了良好的效果。但是,这些优化算法也存在一定的缺陷,例如,在处理多参数问题时,存在过早收敛或易陷入局部最优解等问题。另外,针对各种具体的共形阵列方向图优化问题,将多种智能优化算法互补结合后的混合型优化算法也相继被提出[11-14]。
近年来,随着深度强化学习(Deep Reinforcement Learning,DRL)的蓬勃发展,众多研究者利用DRL算法来解决非线性复杂问题[15-18]。DRL算法可以从经验中进行学习,以层次化的概念来理解问题,即通过简单概念来构建、学习更复杂的概念。因此,本文将DRL应用于复杂共形阵列天线的综合优化过程中,旨在解决复杂共形阵列天线的宽角域波束扫描问题。
1 共形载体分析和算法设计
首先,本文针对平面阵列天线和共形阵列天线的波束扫描性能进行比较和评估,并用阵列有效辐射面积Aeff和总辐射面积Atot的比值来进行表征[19]。对于平面阵列天线,其辐射效率为:
(1)
式中,θs为从法线到背向的扫描角度。通过对各个曲面平台辐射效率的分析,选取圆锥体和圆柱体组成的异构结构作为阵列天线的共形载体。同时,该异构结构因良好的空气动力性能,也是飞行器的常用结构。因此,以飞行器前锥的应用场景为例,比较传统平面阵列天线和共形阵列天线的性能,共形阵列天线的应用场景示意如图1所示。可以发现,平面阵列天线只能部署在有限的区域内,而共形阵列天线可以安装在具有较大面积的天线罩甚至机身周围,大大增加了阵列天线的设计自由度,易于实现宽角波束扫描性能。
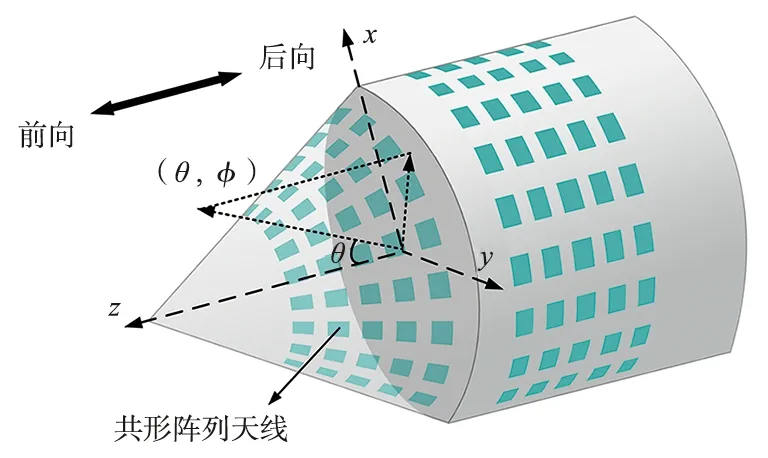
图1 共形阵列天线的应用场景示意Fig.1 Application scenario diagram of conformal array antenna
为使共形阵列天线获得尽可能大的波束扫描角度,将圆锥体的锥角设为120°,同时圆柱体高度等于其半径。需要注意的是,圆柱体高度越大,大角度下的辐射增益也越大。全面考虑辐射单元的最大辐射视角和圆锥—圆柱异型结构的遮蔽效应,对于图1所示的共形于圆锥—圆柱异型结构上的阵列天线,整个波束扫描范围大致可以划分为3部分:0°≤θs≤30°,30°≤θs≤90°和90°≤θs≤180°。
① 当扫描角度θs∈[0°,30°]时,辐射的波束能量全部由圆锥体表面的辐射单元贡献,而圆柱体上的辐射单元由于超过了最大辐射视角而未被激活,此时的有效辐射面积为:
(2)
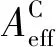
② 当扫描角度θs∈[30°,90°]时,圆锥体和圆柱体上的辐射单元都参与了阵列方向图的综合。此时,有效辐射面积可以表示为:
(3)
式中,φ0为圆柱体与圆锥体的激活扇区角,此处设置为120°。
③ 当扫描角度θs∈[90°,180°]时,圆柱体上的辐射单元为阵列辐射的主体。此时,有效辐射面积为:
(4)
因此,当波束从0°扫描至180°,圆锥—圆柱异型共形阵列天线的归一化有效辐射效率为其辐射效率为:
(5)
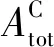
平面阵列天线和共形阵列天线的有效辐射面积对比如图2所示。对比结果可以分为3个部分进行分析和讨论:
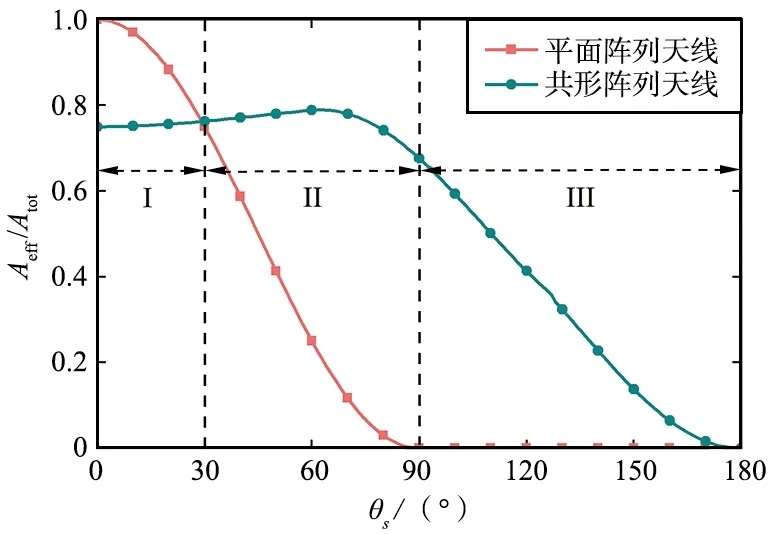
图2 平面阵列天线和共形阵列天线的有效辐射面积随扫描角变化趋势Fig.2 Effective radiation area of planar array antenna and conformal array antenna varying with scanning angle
① 当0°≤|θs|≤30°时,共形阵列天线的辐射效率略低于平面阵列天线。
② 当30°<|θs|≤90°时,共形阵列天线逐渐占据优势地位,其辐射效率随扫描角度的增大仅略有下降。这是因为圆柱体上的天线单元被激活而参与辐射。
③ 当90°<|θs|≤180°时,平面阵列天线已经失能,而共形阵列天线仍保持了良好的辐射性能。
综上,将天线共形于天线罩和机身上可以大大提高波束扫描的范围。接下来将设计一种适用于该复杂共形阵列天线的方向图综合方法,克服传统优化算法存在的维度灾难和局部收敛的问题。
2 DRL算法在共形阵列天线中的应用
共形阵列天线的辐射方向图综合优化问题是一个非线性、非凸的过程,需要采用随机非线性优化算法进行求解。本文研究了一种基于深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)的方向图综合算法,实现了复杂共形阵列天线的宽角域波束扫描性能。
DDPG算法是一种基于策略驱动算法和确定性策略梯度的无模型、离线策略的算法[20]。DDPG将动作策略的探索和动作策略的学习更新分离,动作的探索仍然采用随机策略,而学习的策略则为确定性策略。同时,DDPG中引入了Actor-Critic框架,将策略网络与价值网络分开,并采用了经验复用池来对网络进行非策略训练,以最小化样本之间的相关性。基于上述的特性优势,DDPG算法可用于高维度的动作状态空间,能更好地适应复杂的控制任务。
首先,介绍DDPG应用于阵列综合的过程。DRL算法的核心思想是建立一个从环境状态到智能体行为的映射关系,用于解决决策问题。在本文的应用场景中,智能体是DDPG算法,环境是共形阵列天线,DDPG算法应用于共形阵列天线过程如图3所示。二者的交互过程为:环境接收智能体给出的动作at,然后环境根据动作改变自身的状态st,并将状态反馈给智能体。另一方面,环境根据设定的奖励函数,将此时的动作at和状态st所对应的奖励值rt反馈给智能体。
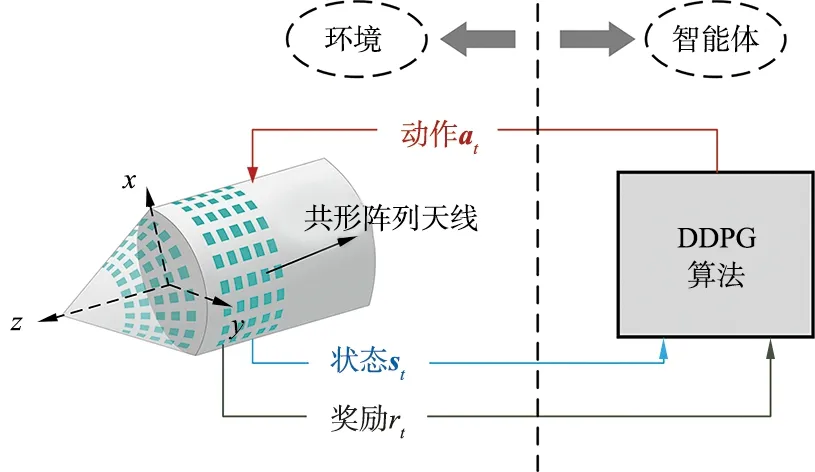
图3 DDPG算法应用于共形阵列天线过程Fig.3 Application process of DDPG algorithm in conformal array antenna
接下来,针对算法中的关键参数进行设计。考虑到阵列天线被共形于一个复杂的曲面结构,以在某种特定的幅度相位分布下实现宽角域波束扫描性能。假设阵列天线包含K个辐射单元,其位置分别为:
P={(x1,y1,z1),…,(xk,yk,zk),…,(xK,yK,zK)}。
(6)
坐标系统的原点与圆柱体顶面的中心重合。因此,天线的辐射方向图为:
(7)
式中,θ,φ分别为俯仰角和方位角;Ak,φk分别为辐射单元pk的激励幅度和相位;Δψk为原点和辐射单元pk之间的相位差;fk(θ,φ)为每个辐射单元的辐射模式。
因此,DDPG算法的目标是找到最优的幅相控制策略来调节辐射波束,以最小化用于计算实际辐射性能和期望需求之间差异的目标函数,即智能体必须根据当前的幅相分布和期望的波束性能〈Gs,θs,φs〉来做出最优的动作策略,确定每个辐射单元的激励幅度和相位,其中Gs是当波束扫描角为(θs,φs)时的目标增益。因而,该优化问题可以联合表示为:
(8)
式中,Gt为t时刻方向(θs,φs)上的增益。
下一步,对DDPG算法的动作空间、状态空间和即时奖励进行设置,具体如下:
① 状态空间:将t时刻的状态空间定义为天线的波束性能,即:
st=〈Gt,θt,φt〉,
(9)
式中,Gt,θt,φt分别为t时刻的增益、俯仰角和方位角。
② 动作空间:本问题中t时刻的动作空间是一组重新排列天线幅相分布的随机幅相对,可以表示为:
(10)
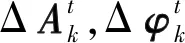
③ 奖励:一般情况下,天线的增益是最重要的指标。因此,奖励rt是由比较t时刻的实时增益和目标方向(θs,φs)的期望增益得到,计算如下:
(11)

基于DDPG算法的共形天线阵列波束扫描算法输入:Gs,θs,ϕs|0≤θs≤5π6,0≤ϕs≤2π{}初始化:策略网络学习概率αA=0.001,价值网络学习效率αC=0.001,软更新参数τ=0.001,折扣因子γ=0.9,回放内存大小 =500,批量大小N=32,总回合数M=5 000,每回合总步数T=10 000以及增益折扣系数 =0.9。价值网络Q(s,a|θQ)和策略网络μ(s|θμ)及它们的权重系数θQ和θμ,目标网络Q′和μ′及它们的权重系数θQ′←θQ,θμ′←θμ。由式(9)计算得到随机状态,式(10)计算得到随机动作,初始奖励r=0。For回合=1~Mdo 初始化观测状态s0和高斯过程nt进行动作探索 For步骤t = 1~Tdo 依据当前策略和探索噪声选择动作at=μ(st)+nt 执行动作at并计算奖励值rt,观察新状态st+1 将元组〈st,at,rt,st+1〉存储至记忆回放池中 从记忆回放池中随机选取N个元组〈si,ai,ri,si+1〉 设yi=ri+YQ′(si+1,μ′(si+1|θμ′)|θQ′) 通过最小化损失来更新价值网络:L=1N∑i(Q(si,ai|θQ)-yi)2 使用抽样的策略梯度更新策略:∇θμJ≈1N∑i∇aQ(s,a|θQ)|s=si,a=μ(si)∇θμμ(s|θμ)|s=si[] 软更新目标网络:θQ′←τθQ+(1-τ)θQ′θμ′←τθμ+(1-τ)θμ′ End forEnd for
3 仿真测试与分析
共形阵列天线构型如图4所示。传统的微带天线阵列被共形于由泡沫制成的圆锥和圆柱平台上。需要注意的是,由于计算资源有限,天线阵列的规模设置为1×17,即式(6)中K=17。另外,圆锥的顶部被截断,一个天线单元被放置在截断处以产生更好的前向辐射性能,且圆锥的基角θb为30°,圆柱的高度h和半径rbtm相等,均为300 mm。
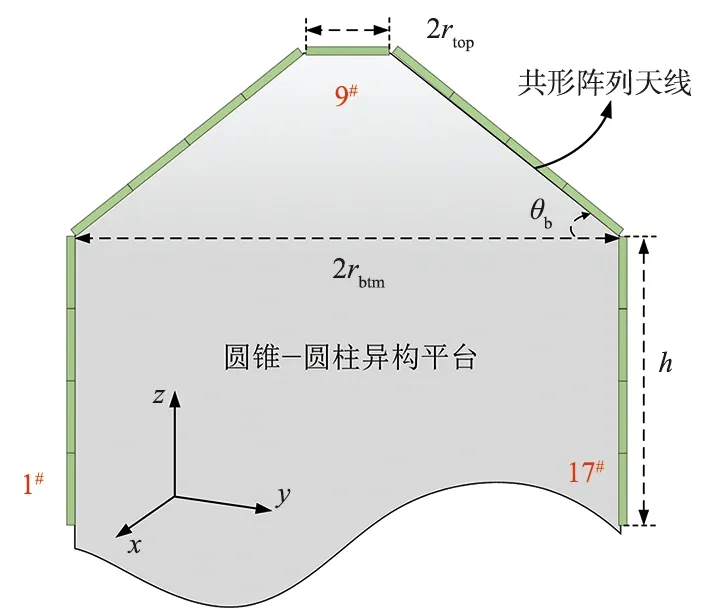
图4 共形阵列天线构型Fig.4 Configuration of conformal array antenna
设置完共形阵列天线的构型后,进行DDPG算法的训练,回合数设置为5 000,最终的评价函数性能如图5所示,证明了DDPG算法是逐渐收敛和稳定的。由于算法前期还处于战略探索和学习阶段,所以在前2 000个回合,算法的初始奖励较低,但呈现逐步增加的过程。在2 000个回合之后,算法的奖励值趋于稳定,徘徊在最大值1附近,如图5(a)所示,说明DDPG已经得到了充分的训练。
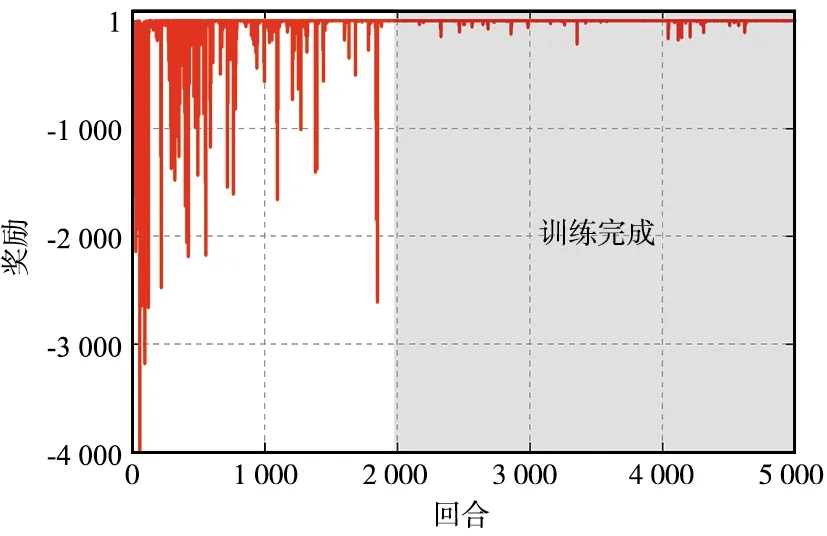
(a) 平均奖励
在完成算法的训练后,对算法进行了400个回合的测试。在每个测试回合中,波束扫描的角度从固定的0°到扫描到某个随机的角度。图5(b)显示了DDPG算法驱动的每个回合波束切换的时间。可以看出,波束的切换时间大多在0.06~0.25 s,平均时间约为0.098 s。这说明DDPG算法可以在非常短的时间内求出目标方向(θs,φs)所需增益Gs对应的阵列天线幅度和相位分布,实现高性能波束扫描。
具体地,基于DDPG算法的共形阵列天线在θs∈{0°,30°,60°,90°,120°,150°}和φs=0°方向上的辐射方向图,如图6所示。可以发现,设计的共形阵列天线实现了几乎覆盖整个视觉空间的波束扫描性能。图6还给出了平面相控阵天线在θs∈{0°,30°,60°}上的辐射方向图,并和共形相控阵天线的辐射性能进行比较。结果表明,当波束扫描角为0°和30°时,共形阵列天线的增益略低于平面阵列天线。然而,当波束扫描角为60°时,共形阵列天线的增益超过了平面阵列天线的增益,与图2中的理论预测一致。此外,当波束扫描角超过90°时,平面阵列天线已经失去有效的辐射性能,而共形阵列天线的辐射性能仍然良好,表明所提出的共形阵列天线在大角度波束扫描方面具有很大优势。
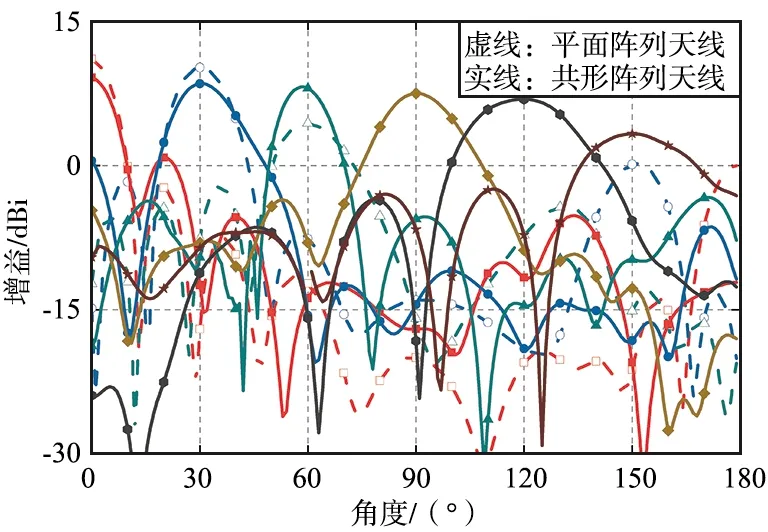
图6 共形阵列天线和平面阵列天线在不同波束扫描角下的辐射方向图对比Fig.6 Comparison of radiation patterns of conformal array antenna and planar array antenna at different beam scanning angles
将所设计的共形阵列天线进行加工、装配和测试来验证基于DDPG算法的共形阵列天线宽角域波束扫描的有效性,共形阵列天线测试环境和加工原型如图7所示。整个阵列天线通过1个1分8和5个1分4功分器进行馈电,其中冗余的支路通过匹配负载进行匹配。另外,还使用了8 bit数字移相器来实现覆盖360°的精度为1.4°的精确移相性能,并预置了功率放大器来弥补每路通道的损耗。每个移相器可以由一个带有8个开关的手动控制器进行精确控制,而辐射单元的激活与否可以通过对应支路的通断进行控制。

图7 共形阵列天线测试环境和加工原型Fig.7 Test environment and fabrication prototype of conformal array antenna
接着,在暗室中对设计的共形阵列天线进行测试。选取了一组目标波束扫描角θs={0°,30°,60°,90°,120°,150°}和φs=0°作为仿真和实测对比,结果如图8所示。仿真结果与实测结果吻合较好,说明基于DDPG算法的共形阵列天线波束扫描算法是有效且准确的。
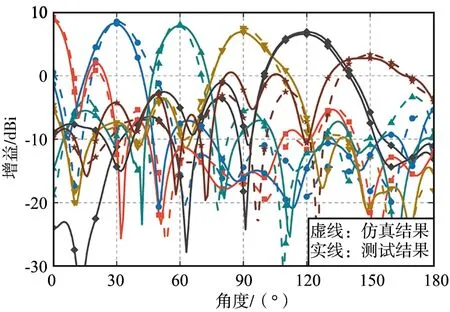
图8 基于DDPG算法的共形阵列天线在不同波束扫描角度下的仿真和测试辐射方向图Fig.8 Simulated and measured radiation patterns of the conformal array antenna at different beam scanning angles based on DDPG algorithm
4 结论
本文提出了一种基于DDPG算法的共形阵列天线宽角域波束扫描算法,实现了几乎全视野空间的波束扫描性能。利用DDPG算法强大的学习能力和非线性拟合能力,有效解决了复杂曲面平台上共形阵列天线的方向图综合难度大的问题。在此基础上,实现了具备宽角域波束扫描和快速波束切换能力的圆锥—圆柱异型共形阵列天线。

