隧道场景下非平稳多簇V2V信道建模与分析
邓炳光,秦启航,孟凡军
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引言
近年来,智能交通系统(Intelligent Traffic Systems,ITS)作为一种改善环境、降低运输成本和缓解交通堵塞的解决方案,引起了人们的广泛关注[1]。而车与车之间的通信是智能交通系统中尤为重要的一环。为了进一步研究车对车(Vehicle to Vehicle,V2V)通信系统,需要采用合理的方法,准确地描述无线传输信道。目前,已有一些V2V信道建模的研究工作,从建模方法上可将现有信道模型分为确定性模型和随机性模型[2]。
确定性模型是结合地图测量信息,根据电磁波传播原理还原信号传播过程,进而建立准确可靠的信道模型[3-5],因此这种方法常用于特定环境下的V2V建模。虽然确定性模型能较好地反映出信道的非平稳性,但由于地图信息在不同场景下测量结果差异较大,极大地限制了其在实际通信系统中的应用。
随机性模型可进一步分为基于几何的统计模型(Geometry-Based Stochastic Model,GBSM)和非几何统计模型(Non-Geometric Statistical Model,NGSM)2类[6]。GBSM中收发两端周围的散射体服从特定分布,通常假设散射体都位于圆环、圆柱和椭圆等规则几何形状上[7-10]。NGSM是通过假设散射体的分布区域和分布特性来获取信道的特征参数。相较于前一种方法,NGSM的优势在于假设过程中考虑到了V2V信道的时间非平稳性,常被用于交叉路口、隧道等特殊场景下的信道建模[11-14]。由于V2V通信中,终端车辆比传统终端设备更便于安装多输入多输出(Multi-Input Multi-Output,MIMO)系统,这一技术的引入实现了对空间的复用,进而达到提升信道容量的目的。文献[15]基于经典双簇模型,引入了大规模MIMO系统,借助生灭算法模拟簇的生命周期。文献[16]提出了一种基于簇的三维V2V非平稳信道模型,结合了单弹跳团簇和双弹跳团簇来模拟散射环境。文献[17]建立了高速列车在圆形隧道场景下的信道模型,考虑信号在视距(Line of Sight,LOS)和非视距(Non-Line of Sight,NLOS)情况下的传播,推导了相关时变统计特性,并在实测数据中得到了较好的验证。
结合上述分析,本文在现有研究基础上,提出一种适用于隧道场景下的三维非平稳V2V信道模型。相较于现有的散射簇信道模型,该模型利用隧道场景的特殊性,简化了时变传播路径的运算量的同时,极大程度地还原了散射体的实际分布情况。首先,假设散射体以簇的形式随机分布在隧道内壁上,采用单簇和多簇来模拟散射环境。其次,引入时变的角度值和传输路径长度来描述信道的非平稳性。最后,利用几何关系推导了所提模型的时空相关函数(Space-Time Correlation Function,ST-CF)和多普勒功率谱密度(Power Spectral Density,PSD)等统计特性,并进行了仿真计算,将结果与理论模型进行了对比分析。
1 系统信道模型
1.1 系统模型描述
本文将隧道抽象为一个半圆柱体,提出了一个宽带非平稳的几何半椭圆散射V2V信道模型,如图1所示。图中,隧道可视作长度为L、截面半径为R的半圆柱体,MT和MR分别代表V2V通信时的发送端和接收端,二者均处于匀速运动的状态。

图1 隧道场景下三维多簇V2V信道模型Fig.1 3D multi-cluster V2V channel model in tunnel scenario

该模型采用MIMO通信系统,收发端天线均配备有均匀线性阵列(Uniform Linear Array,ULA),用方位角ψT/R和俯仰角θT/R来描述收发端天线在三维空间中的状态。
1.2 复冲击响应
本文提出的模型中,MIMO信道的复冲击响应(Complex Impulse Response,CIR)可以用矩阵H(t)=[hpq(t,τ)]MR×MT来表示。其中,hpq(t,τ)为MT第p(p=1,2,…,MT)根发射天线和第q(q=1,2,…,MR)根接收天线之间的复冲击响应,包含了LOS分量和NLOS分量2个部分:
(1)
式中,τLOS为传播信号从发送端直接到达接收端的传播时延;τNLOS为信号从MT发射天线发出,经散射体反射后到达MR接收天线的平均传播时延。簇的数量由L个单簇和M对双簇两部分叠加组成。所以,NLOS的CIR可进一步表示为:
(2)
对于LOS成分,信道冲击响应可以为:

(3)
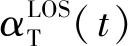
半圆柱隧道场景下V2V信道模型中SB成分的几何关系如图2所示,信号从发射天线出发,经过第l个簇的第nl个散射体反射后到达接收天线,其复冲击响应增益可表示为:

图2 半圆柱隧道场景下V2V信道模型中SB成分的几何关系Fig.2 Geometric relationship of the SB components in the V2V channel model in the semi-cylindrical tunnel scenario
(4)

ξpq,nl(t)=ξpnl(t)+ξqnl(t),
(5)
式中,ξpnl为发送端第p个天线到散射簇中第nl个散射体的距离;ξqnl为接收端第q个子天线到散射体nl的距离:
(6)
(7)
式中,ξTnl为MT侧天线阵列中心位置到散射体nl的距离;ξRnl为MR天线阵列中心位置到散射体nl的距离。根据模型中几何关系可以得到ξTnl和ξRnl的闭式表达式为:
(8)
(9)
散射体nl的坐标(xnl(t),ynl(t),znl(t))可以通过MT的位置计算,表示为:
(10)
(11)
(12)

(13)
(14)
半圆柱隧道场景下V2V信道模型中MB成分的几何关系如图3所示。

图3 半圆柱隧道场景下V2V信道模型中MB成分的几何关系Fig.3 Geometric relationship of MB components in V2V channel model in semi-cylindrical tunnel scenario
主要关注2个簇,分别是位于近发送端的第一次反射的散射簇和近接收端的最后一次反射的散射簇。2个散射簇之间的传播路径用虚拟链路来表示,其复冲击响应增益可表示为:
ej(φnm-2πfcξpq,nm,1,nm,2(t)/c)×
(15)

ξpq,nm,1,nm,2(t)=ξpnm,1(t)+ξqnm,2(t)+τnm,1nm,2(t)c,
(16)
式中,ξpnm,1为信号从发射端第p个子天线到散射簇中第nm,1个散射体之间的传播距离;ξqnm,2为信号从接收端第q个子天线到散射簇第nm,2个散射体之间的传播距离。一对簇中的虚拟链路平均时延可通过指数分布随机产生:
(17)
(18)
式中,ξT,nm,1为MT天线阵列中心位置到散射簇中第nm,1个散射体的距离;ξR,nm,2为MR天线阵列中心位置到散射簇中第nm,2个散射体的距离。根据模型中几何关系可以得到ξT,nm,1和ξR,nm,2的闭式表达式为:
ξT,nm,1=[(xnm,1-xT)2+
(19)
ξR,nm,2=[(xnm,2-xR)2+
(20)
散射体nm,1可以通过发送端MT的位置确定,可以表示为:
(21)
(22)
(23)
类似的,可以通过MR的位置确定散射体nm,2的位置。
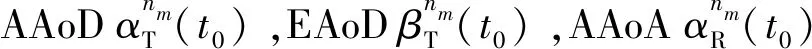
(24)

(25)
同时,为了考虑时变方位角对于模型统计传播特性的影响,且VMF分布已被广泛地用于描述信号方位角的分布,本文采用VMF分布来描述隧道内散射体的分布。因此,其概率密度函数可表示为:
(26)
式中,μα和μβ为方位角的均值;I0(·)为零阶第一类修正贝塞尔函数;ki为方位角的集中程度。为简化分析,本文假设所有的簇都具有相同的k值。
对每一个簇都有相应的一个功率均值。记Pl为单簇条件下第nl个簇的功率,Pm为双簇条件下第nm对簇的功率,双簇中任一单个簇对应的功率为Pm/2。参考WINNER II模型[19]中的功率产生方法,第i簇的功率表示为:
(27)

2 模型的统计特性
2.1 时变的时空相关函数
基于所提出的信道模型,其时空相关函数可以表示为:
(28)
本文假设SB分量和MB分量二者之间相互独立,因此式(28)可以改写为:
(29)
式(29)中的LOS分量、SB分量和MB分量的空时CF分别表示如下:
LOS分量:
(30)
SB分量:
(31)
MB分量:

(32)
把Δt=0代入式(29),可得到空间CCF的表达式:
ρh(t,δT,δR,Δt)=ρh(t,δT,δR,0)。
(33)
令式(29)中天线间的间距δR=0和δT=0,可以得到时变的ACF,表示为:
rh(t,Δt)=ρh(t,0,0,Δt)。
(34)
2.2 时变的空间多普勒PSD
因多普勒PSD和ACF是一对傅里叶变换对,因此对式(34)进行傅里叶变换,得到空间多普勒PSD的表达式为:
(35)
3 数值结果与分析
本节将对信道模型进行仿真和分析,探讨不同条件下参数对通信系统的影响。为不失一般性,部分仿真参数设置如下:R=6 m,L=60 m,MT=MR=2,fc=5.9 GHz,Kpq=1,vT=vR=10 m/s,γT=0,γR=π,ψT=ψR=θT=θR=0,Nl=Nm=40。发射端的初始坐标表示为(xT,yT,zT)=(4 m,3 m,1 m),接收端的初始坐标表示为(xR,yR,zR)=(56 m,-3 m,1 m)。仿真中,参考WINNER II模型[20]中关于室内场景和高速移动场景参数,设定隧道内壁中随机分布着8个簇,这些簇的位置可以根据收发端的初始位置和方位角初值计算得到。
根据式(33)可以得到所提模型在不同k值条件下对应的空间CCF,理论和仿真结果如图4所示。
由图4可以看出,空间CCF的值在天线间距δT=δR=0时最大为1,随着天线间距的增加,空间CCF震荡快速衰减并最终趋近于0,这正是由于信道的非平稳性导致的。参数k用来控制角度的集中程度,越大的k值表示角度的分布越集中在均值附近。随着k值降低,散射环境越趋向于各向同性,空间互相关函数的曲线越平滑,空间相关性也越低。
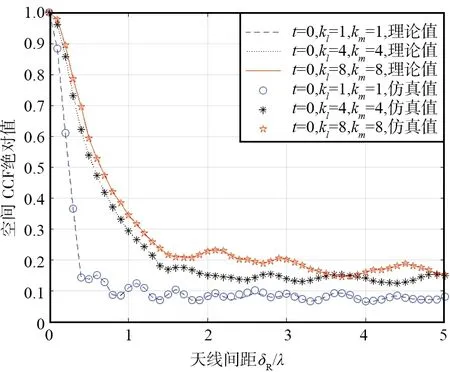
图4 不同k值对应的空间CCF理论和仿真结果Fig.4 Theoretical and simulated values of spatial CCF corresponding to different k values
将式(13),式(14),式(24)和式(25)带入式(34),可以得到所提模型时变的时间ACF函数曲线。在不同时刻t(t为0,2,10 s)对应的时间ACF的理论和仿真结果如图5所示。可以看出,当MT和MR的运动时间从0 s增加到10 s时,时间ACF曲线差异显著,时间的相关性明显增加。在很小的时间间隔内,仿真值与理论值的高度拟合,也验证了模型的有效性。
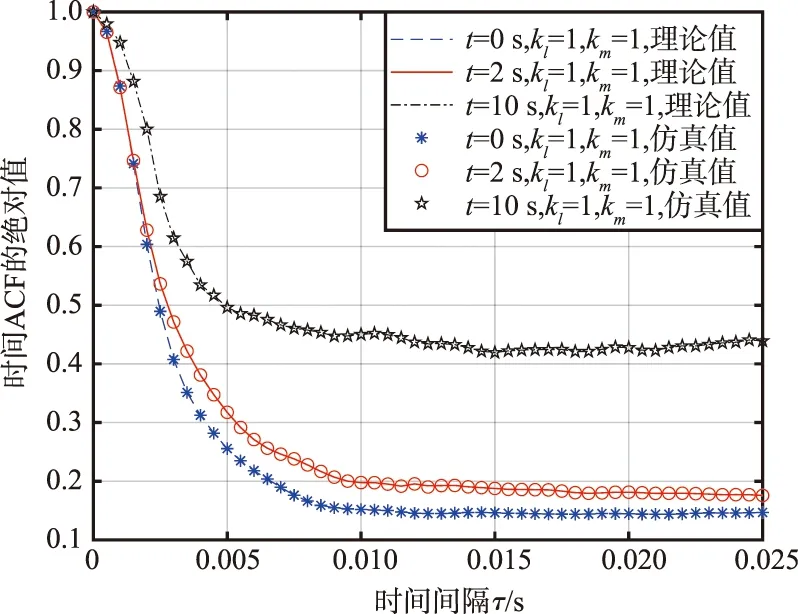
图5 不同时刻下对应的时间ACF理论和仿真结果Fig.5 Theoretical results and simulation values of temporal ACF corresponding to different times
在不包含LOS分量的情况以及包含LOS分量的情况下不同时刻下时间ACF的仿真结果如图6所示。在包含LOS时,时间ACF相关性要比仅考虑NLOS的时候高得多。此外,时间ACF随着时间t从0 s增加到2 s而增加。

图6 不同时刻下(不)包含LOS分量的时间ACF理论值Fig.6 Theoretical temporal ACF values (without) including LOS components at different times
在不同时刻下,不同k值对于多普勒PSD仿真结果的影响如图7所示。由于V2V信道的非平稳特性,PSD随着时间的不同有明显的变换。当时间从t=0 s变化到t=2 s时刻时,PSD有增长的趋势。此外,在不同的k值对应的多普勒PSD也会随着k值的增加而增加,且差别较为显著。

图7 不同时刻下不同k值对应的多普勒PSDFig.7 Doppler PSD corresponding to different k values at different times
4 结束语
本文针对半圆柱隧道环境中V2V通信场景,提出了一个三维的非平稳多散射簇V2V信道模型。在所提模型中,结合了传统几何模型计算量小和基于簇的模型更贴合实际场景的优点,可以通过调整相应的隧道参数,适用于所有的类圆柱形隧道中的V2V通信系统。进一步推导并研究了包括时间ACF,空间CCF以及空间多普勒PSD在内的信道统计特性。数值分析结果表明,考虑收发端时变的方位角和传播距离,时间变化和不同的角度分布都会对统计特性产生较大影响,证明了该模型能较好地体现V2V信道的非平稳特性。最后,所有统计特性的仿真结果与理论值曲线贴合度较高,验证了模型的正确性。在大规模MIMO通信系统中,由于天线尺寸的增加,平面波前假设不再成立,同时大规模MIMO天线怎样的排列形态对于V2V通信有更大的增益,这都是V2V信道建模领域接下来需要关注的重点。

