融合星间数据卸载的敏捷卫星任务规划
尉 欢,刘志慧,王俊义,董 涛
(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004;2.北京卫星信息工程研究所天地一体化信息技术国家重点实验室,北京 100095)
0 引言
不同于传统卫星,敏捷卫星具有三轴姿态[1]特性。因此,其具有更高的灵活性和更宽的观测时间窗。敏捷卫星的姿态转换需要转换时间且消耗星载电池电量,对规划任务序列有一定的影响。此外,受卫星体积限制,星载电量和内存容量是有限的,如何在这种高动态场景下有效地利用有限的星载资源获取尽可能多的观测收益是卫星任务规划研究人员不断追求的目标。
对于这种高动态问题,可以利用滚动水平优化策略[2-3],将动态过程分解为一系列时间段,通过在时间段内优化规划方案,实现任务的动态调度。而对于观测任务时间窗约束和观测卫星星载资源约束,现有的敏捷卫星任务规划研究主要包括基于规则[4-7]或基于图[8-10]的算法。基于规则的方法是手工编码逻辑,计算效率高,但是对于不同的模型适应度低。基于图的方法简练且适应度高,但图不能直接扩展将星载资源纳入规划过程。因此,以往针对该问题采用资源预规划[11-12]策略,将问题分解为任务资源预分配和时间序列规划2个子问题,有效提高规划效率。然而由于空间环境的不确定性,预规划的任务可能发生变化,所以重规划策略[3,13]的应用更为广泛,通过对预规划后的观测任务队列进行重调整,更加有利于减短寻优所需时间。以上观测任务规划方法无法从根本上解决星载内存有限这一问题,仅考虑了下传任务的观测卫星任务规划研究也无法克服我国的地面站多位于国内、观测卫星直接将数据下传至地面站的下传窗口有限的问题。实际应用中,一味追求星载内存容量会导致卫星体积过大和成本过高。目前卫星星座已经成为研究热点,联合多星任务卸载的应用也突飞猛进,现有的任务卸载研究[14-15]多是假设所需要的观测数据已经收集并存储到卫星中,研究重点是多星协同下载数据至地面站,而不是观测任务的规划。理论上,利用卫星星座融合任务卸载的观测任务规划不但可以减轻卫星存储资源的压力,而且可以提高地面站接收数据的有效性和及时性,具有重要的研究意义。
针对以上问题,本文综合考虑了卫星姿态转换、时间依赖的观测收益、星载电池周期性充电,创新性地构建了利用下载任务和卸载任务优化观测卫星任务规划的模型。算法上,提出了包含预规划和重规划2级资源分配方法的滚动双规划算法框架。综合基于规则和基于图的算法,提出了采用2级约束的基于图适应度的改进遗传算法(Graph-based Fitness Evaluation Improved Genetic Algorithm,GFEGA)。
1 系统模型描述及分析
1.1 系统模型
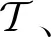
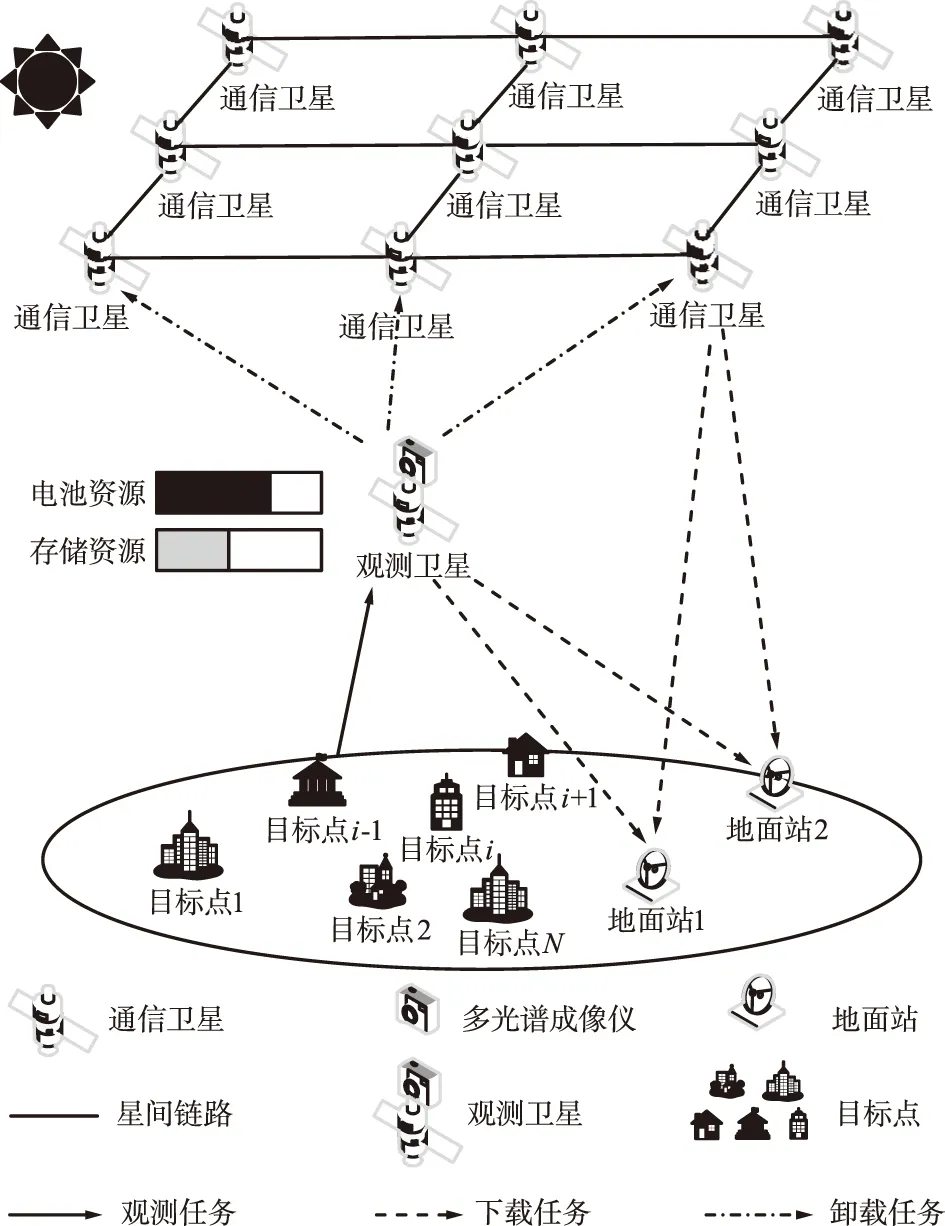
图1 系统模型Fig.1 System model
集合1:观测任务集合
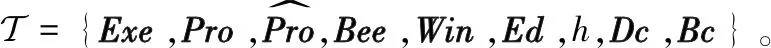
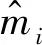
集合2:电池资源集合
Bcap是一个常数,表示星载电池容量。Bcur也是一个常数,表示当前可用的星载电池电量。C={[cs1,ce1],[cs2,ce2],…,[csk,cek],…}表示电池充电时间区间的集合,其中csk和cek分别表示第k次充电时间区间的开始时刻和结束时刻。Br={br1,br2,…,brk,…}表示充电速率的集合,其元素brk表示在第k个充电时间区间内的充电速率。
集合3:存储资源集合
Dcap是一个常数,表示星载存储容量。Dcur也是一个常数,表示当前可用的星载存储容量。Down={[ds1,de1],[ds2,de2],…,[dsl,del],…}表示数据下载时间区间集合,其中dsl和del分别表示第l个数据下载时间区间的开始时刻和结束时刻。Dr={dr1,dr2,…,drl,…}表示数据下传速率集合,其元素drl表示在第l个数据下载区间内数据下传的速率。βd表示下载单位数据消耗的电量。OFF={[os1,oe1],[os2,oe2],…,[osg,oeg],…}表示数据卸载时间区间集合,其中osg和oeg分别表示第g个数据卸载时间区间的开始时刻和结束时刻。Or={or1,or2,…,org,…}表示数据卸载速率集合,其元素org表示在第g个数据卸载区间内数据卸载的速率。βo表示卸载单位数据消耗的电量。
1.2 问题分析

(1)
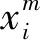
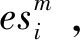
(2)
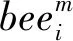
(3)
(4)
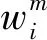
三是卸载任务选择变量集合A,其元素∂ζ,ζ=1,2,3,…,表示观测卫星在时隙ζ内是否执行卸载任务,其值为0或1,1表示执行卸载任务,0表示不执行卸载任务:

本文规定观测任务、下传任务和卸载任务在时间上互不影响,可以同时执行,它们相互之间不存在时间约束。以上3种任务之间的冲突源于观测卫星星载存储资源和电量资源有限。敏捷观测卫星任务规划的约束具体如下所示。
1.2.1 时间约束
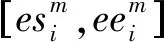
(i∈{1,2,…,N},m∈{1,2,…,M})。
(5)
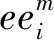
(i,j∈{1,2,…,N},m∈{1,2,…,M}),
(6)
式中,τi,j为卫星从观测目标点i所需姿态转换到观测目标点j所需姿态的姿态转换时间。观测任务时间约束的详细信息如图2所示。
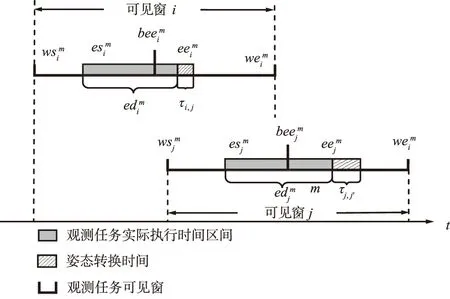
图2 观测任务时间约束Fig.2 Time constraints for observation tasks
1.2.2 资源约束
本文在卫星任务规划过程中,将时间划分成较多个规划单元,在处理资源约束的过程中又将规划单元划分成多个较短的时隙,时隙划分依据观测可见窗,保证在每个时隙中最多只有一个观测任务。时隙划分如图3所示,时隙ζ-1和ζ+1内无观测任务,时隙ζ内有一个观测任务。假设在时隙ζ中,即观测任务i的第m个可见窗中,有K个电池充电时间区间,L个下载任务可见窗和G个卸载任务可见窗。
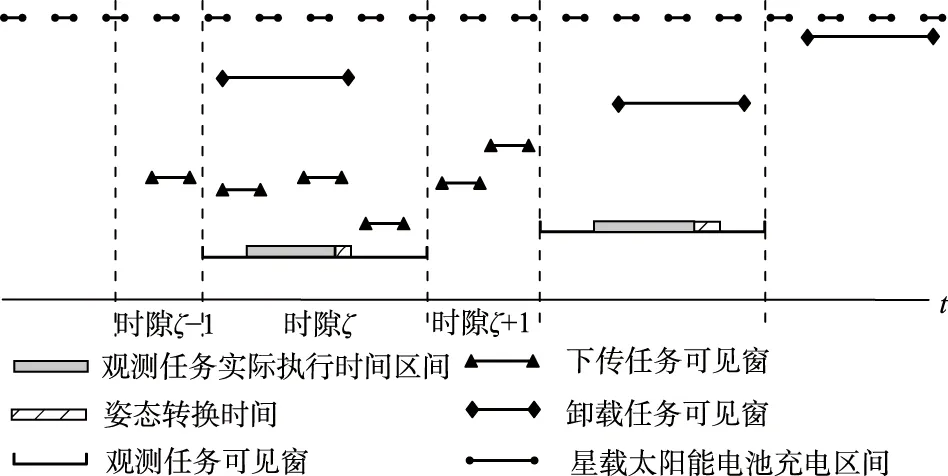
图3 规划单元内时隙划分示意Fig.3 Diagram of time slot division in planning unit
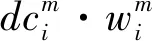
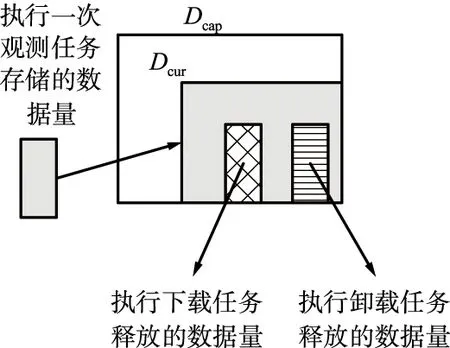
(a) 存储资源约束
(7)

(8)
式中,αi,j表示卫星从观测目标i所需姿态转换到观测目标j所需姿态消耗的电量。
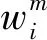
1.2.3 优化问题
(9)
最终,建立优化问题如下:
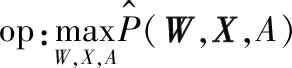
(10)
2 算法设计
以上所提的优化问题是一个动态的混合整数规划,求解复杂度高,属于NP-hard问题[16-17]。因此,本节首先建立了一个滚动双规划的框架,将该动态问题转换为静态问题——混合整数规划;然后,设计了GFEGA来求解该静态问题。具体介绍如下。
2.1 滚动双规划框架
滚动双规划框架包括预规划和重规划,预规划是为了预先公平分配电量和存储资源,重规划是为了调整分配资源。时间被划分为多个长度为LU的规划单元,相邻规划单元之间存在时间交叉避免硬性分割,先对这些规划单元内进行资源预规划。NU个规划单元组成一个规划组,对每个规划组进行Γ次重规划,然后沿时间轴向前移动Ns个规划单元,再取NU个规划单元重复上述操作,直到Ω时间段内的所有任务都被规划完,具体情况如算法1所示。为方便起见,规划单元长度LU小于观测卫星绕地运行周期。

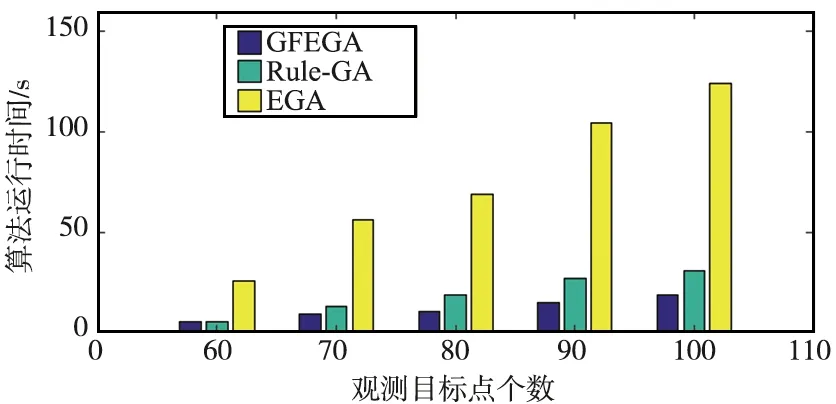
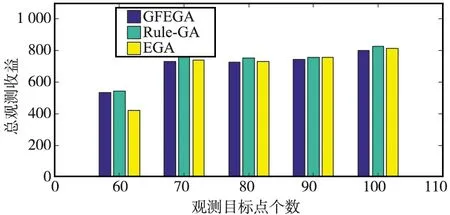
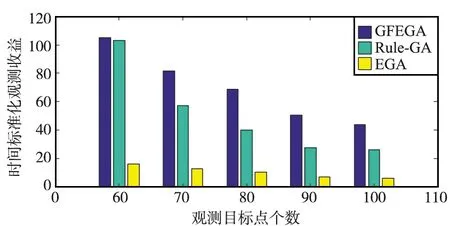
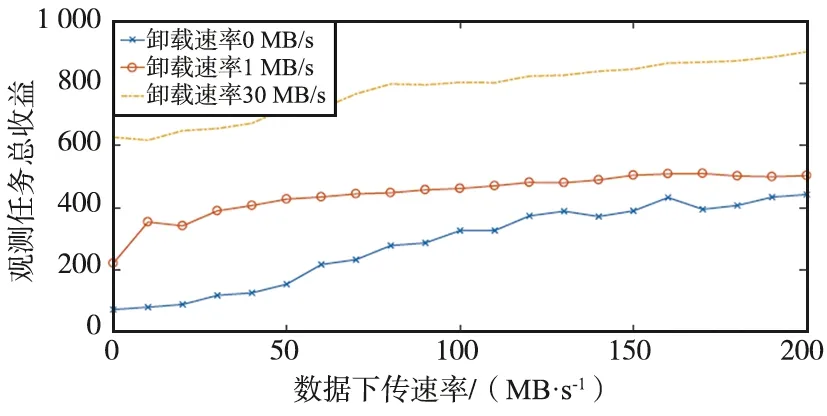
算法1 滚动双规划框架输入:1: 中的常量, , ,Ω,LU,NU,Γ,Ns(Ns 2.1.1 资源预规划 资源预规划的目的是提前预估出规划范围内所需的总资源量,然后将资源公平地分配给每个规划单元,避免时间上靠后的任务因缺乏星载资源而无法执行,资源预分配的步骤如下: 步骤1以24 h为参考时间,预估该参考时间内可恢复的资源总量R1和需要消耗的资源总量R2,其中根据电池充电区间个数预估可恢复电量,根据下载可见窗个数预估可恢复存储容量。根据观测可见窗个数和下载可见窗个数预估消耗资源; 步骤2预估每个规划单元内可选任务消耗的资源总量rε,ε=1,2,…,NU; 步骤3预估每个规划单元的预分配资源reε=rε×(R1/R2),ε=1,2,…,NU。 2.1.2 资源重规划 重规划的目的是调整资源分配,给资源利用率高的任务分配更多的资源,以提高总观测收益。资源重分配的步骤如下: 步骤1将所有规划单元内未使用完的预规划资源相加,形成第一级资源池Pool1,它是一个标量; 步骤2将每个规划单元已使用了的预规划资源按重规划调优参数ratio(本文ratio仿真中取值0.1)分别取出一部分,不相加,形成第二级资源池Pool2,它是一个矢量; 步骤3给由于资源不足而无法执行下载任务的规划单元重新分配资源,先使用第一级资源池Pool1,不够再使用第二级资源池Pool2; 步骤4将规划单元按照资源利用率降序排列,先给资源利用率高的规划单元分配资源,同样优先使用第一级资源池Pool1,规划单元ε的资源利用率fε表示在规划单元ε中,观测任务总收益puε与消耗的资源总量ruε的比值,即fε=puε/ruε,ε=1,2,…,NU; 注:以上资源既可以表示电池资源也可以表示存储资源。 图5 GFEGA流程Fig.5 GFEGA flow chart 2.2.1 基于图计算适应度的规则 观测任务序列的总观测收益是适应度的表征,本文提出利用2级约束求解染色体适应度,第1级约束是观测任务时间约束,根据规划单元内观测任务实际开始时间和观测收益构造有向无环图,利用最短路径算法选择出满足时间约束的情况下总收益最高的规划序列。第2级约束是星载资源约束,按照优先分配电量用于下载任务,若内存紧张限制存放观测数据,则执行卸载任务,释放存储空间的原则,选择出满足资源约束的规划序列。具体操作如下: 步骤1设有向无环图G=(V,E),其中,V是顶点集,E是边集,初始化V,E=∅; 步骤2顶点集V中添加原点v0、终点vn+1,然后依次添加表示观测任务的顶点vi,i=1,2,…,n,n为规划单元内观测任务数量; 步骤5利用Bellman-ford算法[18]求解有向无环图G的最短路径,除原点v0和终点vn+1外,最短路径上的顶点是满足时间约束的最佳可执行观测任务,将相应的选择系数twi标记为1,不满足的标记为0; 步骤6根据优先执行下载任务再执行观测任务,内存资源紧张时执行卸载任务的策略以及式(7)和式(8),将既满足时间约束又满足资源约束的观测任务选择系数rwi标记为1,否则标记为0; 步骤7将rwi的值赋值给wi,根据式(9)更新观测任务序列的总观测收益。 2.2.2 分组轮盘赌选择 通过计算每个个体的适应度可判断其优劣,个体的适应度是通过个体的观测收益来衡量的,观测收益越高,适应度越强,个体越好。传统的轮盘赌算子中,被选中个体的概率完全由个体的适应度决定,这导致适应度高的个体不断繁衍,不利于种群的多样性,甚至导致过早收敛于局部解。本文中分组轮盘赌选择算子是传统轮盘赌算子和随机选择的混合,具体操作如下。 步骤1定义种群中个体数量为ξ,分组数为ω,0≤ω≤ξ; 步骤2根据个体观测收益降序排列; 步骤3将重新排序后的种群划分成ω组,每组的被选概率等于该组内所有个体的观测收益之和除以种群的总观测收益; 步骤4利用轮盘选择出一个组,然后在该组中随机选择一个个体。 2.2.3 交叉变异规则 在规划单元中,观测任务可见窗序列根据相应的观测任务实际开始时间排序编号,因此每个染色体上的每个基因都有一个标记编号。每条染色体代表一个观测任务可见窗序列,染色体上的每个基因代表一个观测任务可见窗,基因中的0和1是任务选择变量,1表明该观测可见窗内执行观测任务,0则表明该观测时间窗内不执行观测任务。 交叉变异的规则为,首先随机选择交叉基因序列号;通过分组轮盘赌选择出2条染色体作为父代1和父代2;分别从父代1和父代2中取出交叉基因序列号对应的基因;从父代1中取出的基因按顺序插入到父代2中,同理,从父代2中取出的基因按序插入到父代1中;每条染色体随机选择2个基因改变其任务选择变量完成变异操作;最后,将新生成的2个子代加入种群。交叉变异的规则如图6所示。 图6 交叉变异规则示意Fig.6 Schematic diagram for rules of crossover and variation 为了验证所提模型的可行性和算法的有效性,本文开展如下仿真实验。实验环境包括配置为Windows 10 Inter(R) Core(TM) i5-10400 CPU @ 2.9 GHz,16 GB RAM的计算机,以及仿真软件Matlab2018b和STK11。 观测卫星轨道相关参数如表1所示。通信卫星参数依照铱星星座设置66颗,即6个轨道面,每个轨道面11颗通信卫星,轨道高度780 km,轨道倾角86.4°,设置观测卫星与通信卫星相距1 000 km以内且可见即可建立卸载传输链路。地面站设置10个,相关参数如表2所示。观测任务的部分参数设置如表3所示。 表1 观测卫星参数Tab.1 Parameters of observation satellite 表2 地面站参数Tab.2 Parameters of ground Stations 表3 观测任务参数Tab.3 Parameters of observation tasks 在滚动双规划框架下,将仿真时间范围Ω设置为12 h。规划单元长度LU是观测卫星绕地运行周期的一半。4个规划单元组成一个重规划组,即NU=4。重规划次数Γ为5,滚动步长Ns为2。遗传算法的交叉概率和变异概率如无特殊说明,均分别设为0.3和0.5。 以下设置了2组仿真实验,其中用到3.1的参数如无特殊说明,均不变。 第1组仿真实验是为了验证本文设计的GFEGA的优劣性,对比算法EGA[19]未使用任何编解码规则,Rule-GA[5]采用了一种基于整数序列编码和从后向前解码的规则。本文设计的GFEGA则基于浮点加二进制序列编码和有向无环图解码的方法。该组对比仿真实验设置了5个仿真场景,每个场景对应的观测目标点个数分别为60,70,80,90,100,下传速率均设为100 MB/s,卸载速率均设为300 MB/s,每个场景分别采用EGA,Rule-GA和GFEGA在滚动双规划算法框架下进行15次实验,并将15次的算法运行时间和总观测收益取平均值。 平均运行时间如图7所示,总体来看,随着观测目标的增加,任务规划所需时间也在增加,这符合数据量越大运算时间越长的实际情况。GFEGA的运行时间远短于EGA,当目标点较少时,GFEGA与Rule-GA相比差别不大,但当目标点更多时,GFEGA的运行时间比Rule-GA更短。 图7 算法运行时间Fig.7 Running time for algorithms 平均总观测收益如图8所示,随着目标点的增加,总观测收益也在增加,然而当观测任务过多,星载资源无法满足任务所需资源时这种增加的趋势不再保持。 图8 总观测收益Fig.8 Total observation profits 时间标准化的收益是指平均总观测收益除以相应的平均运行时间,是对总观测收益和规划时间的综合考虑,如图9所示,GFEGA具有最佳的性能。 图9 时间标准化的总观测收益Fig.9 Total observation profits with time normalized 第2组实验是为了验证观测任务规划中将数据卸载至卫星星座释放内存压力的可行性。仅改变观测卫星数据下传速率和卸载速率,每个场景采用GFEGA在滚动双规划框架下进行15次实验,并将15次的总观测收益取平均值,结果如图10所示。 图10 受下传速率和卸载速率影响的总观测收益Fig.10 Total observation profits with different download rates and offload rates 由图10可以看出,相同仿真时间范围内,随着观测卫星数据下传速率的增大,获得的总观测收益增多,在数据下传速率不变的情况下,随着观测卫星数据卸载速率的增大,获得的总观测收益也在增多。这表明,观测卫星星载资源有限,及时下传和卸载数据有利于腾出存储空间用来存放更多的观测任务。 针对时间约束和资源受限的敏捷卫星任务规划问题,本文不但综合考虑了任务下传、卫星姿态转换、星载电池充电以及时间依赖的观测收益,而且创新性地引入了星间数据卸载,分析了星间数据卸载对观测卫星收益的影响,当观测卫星星载存储资源紧张时,通过将其内存数据卸载到通信卫星星座,可执行更多观测任务;但是观测数据经过通信卫星再下载至地面站将会消耗额外的通信资源,增加数据传输成本。所以任务卸载实质上是一种资源置换,用通信资源和电量资源换取存储资源。平衡好这种资源置换的关系就可以获得不错的收益,这为今后研究观测卫星任务规划提出了一种新的思路。观测任务在不同通信卫星间卸载的机制与策略有待进一步研究。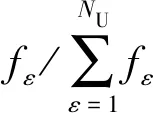
2.2 基于图适应度的改进遗传算法
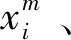
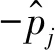
3 仿真实验
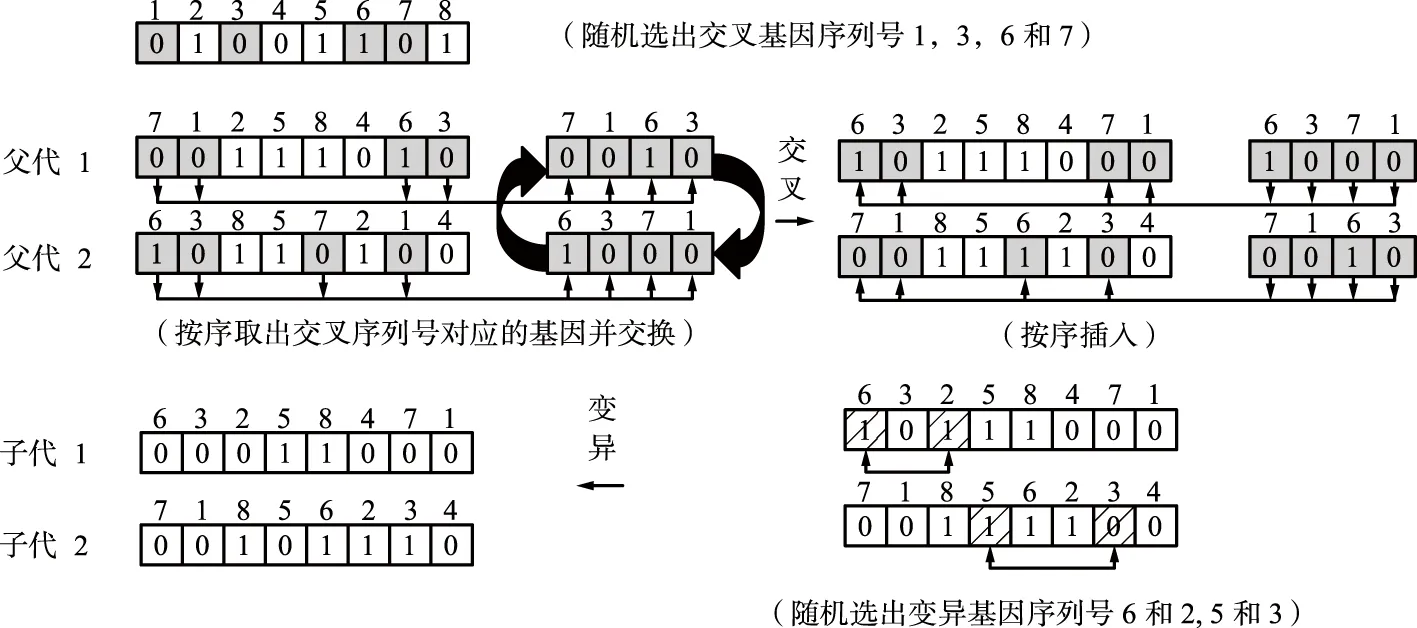
3.1 参数设置

3.2 仿真结果
4 结束语

