基于格的后量子密码系统研究

张 贺，王 鹏，李思照

(哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001)

0 引言

后量子密码(Post-Quantum Cryptography，PQC)又称抗量子密码，是能够抵抗量子计算机对现有密码算法攻击的新一代密码算法。因为量子计算机的出现，现有的绝大多数公钥密码算法(RSA，Diffie-Hellman和椭圆曲线等)能被足够大且稳定的量子计算机攻破[1]，可以抵抗这种攻击的密码算法能够在量子计算和其之后时代存活下来，所以被称为“后”量子密码。

密码学的发展经过了4个阶段：古典密码学、近代密码学、现代密码学和新兴的量子密码学。其中，古典密码学的经典算法主要有凯撒加密和换位加密[2]等；近代密码学则是以DES为代表的对称密码学，随后非对称加密算法标志着公钥加密成为新的主流[3]。公钥加密的原理一般是基于对应数学的问题在计算机上的难解性进行的，但是，量子计算机的出现使得这一难解的过程可以在有限的时间内得到解决。因此，量子密码学应运而生，它利用了单光子的量子性质[4]，保证了数据传输的可证性安全。

标志着密码学进入量子密码学新时期的算法主要是1994年彼得·秀尔[5]提出的Shor算法和1996年Lov Grover[6]提出的Grover算法。Shor算法可以以多项式时间求解周期函数的周期，而RSA、椭圆曲线等密码体制基于的大整数分解问题和离散对数求解问题，都可以转化为周期函数求解周期的问题，因此Shor算法可以在有限时间内破解现有的RSA方案等公钥加密方案。Grover算法又称为量子搜索算法，是一种用于非结构化搜索的算法。

PQC按照其数学原理主要可以分为4种[7]：基于格的PQC体制、基于编码的PQC体制、基于哈希的PQC体制和基于多变量多项式的PQC体制。其中，基于格的PQC算法在安全性、公私钥尺寸和计算速度上有着更好的平衡，主要表现在：第一，Ajtai等人[8]在数学层面上证明了格中一般的困难问题与NP困难问题的难度等价，有着较强的安全性；第二，基于格的PQC的应用场景丰富，在传统的公钥加密、数字签名和密钥交换等领域都有着优秀的表现；第三，基于格的密码体制在硬件上的实现很灵活，可部署场景广泛，在资源受限和资源丰富的场合都可以应用[9]。因此，基于格的PQC体制被很多人认为是最有前景的PQC算法。

与常规的把复杂问题转换为简单问题再求解不同，密码算法的安全性完全要依赖于难解的数学问题，在有限的时间内无法求出解。与在软件上执行的PQC算法相比，硬件执行的效率是软件上的数十倍，甚至上百倍。在一些军方和医疗等复杂的应用场合[10]，需要高速的执行来缩短加解密时间，因此关于PQC算法在硬件上的研究就显得十分必要。

1 基于格的PQC体制发展现状

量子计算机的出现对于目前的密码体制造成了巨大的冲击，各个国家都开始积极地推动PQC标准的制定。最具代表性的是美国国家标准与技术研究所(National Institute of Standards and Technology，NIST)。早在2009年，NIST就启动了PQC计划来标准化一个或多个PQC方案。2015年4月，NIST举办了“后量子世界的网络安全”研讨会，对未来的标准化进行了讨论[11]。在2016年，NIST正式宣布进行NIST PQC算法征集[12]，邀请世界各国学者提交PQC方案，再经由评定选出适合标准化的算法。

1.1 评估标准

NIST的标准化评定对于算法的评估主要分为3个方面，包括安全性、成本和性能以及算法和实现特征[13]。具体来说，安全性是评估PQC算法最为重要的因素，需要遵循传输层安全协议(Transport Layer Security，TLS)、安全外壳协议(Secure Shell，SSH)和网络密钥交换协议(Internet Key Exchange，IKE)等一系列互联网协议。NIST对算法的安全强度定义了5种安全级别[14]，如表1所示，以更好地比较提交算法的安全强度等级。成本是评估候选算法时的第二重要标准，包括计算效率和内存需求，具体包括公钥、密文和签名的大小，密钥生成，公钥和私钥的计算效率以及解密的成功率，所有提交算法的提交者需要提供NIST参考平台的性能评估。NIST更希望接受灵活性大的候选算法，这有利于在各种平台上高效地运行，同时可以通过指令集的扩展来提高算法性能。

表1 NIST规定的算法安全级别Tab.1 Algorithm security levels specified by NIST

1.2 算法征集情况

截止现在，NIST已经进行了3轮对广泛征集的PQC算法的评估，提交的算法分为公钥加密、密钥封装方案和数字签名方案。在2017年12月，NIST对征集到的69份PQC算法方案进行了评估，其中包括20份数字签名方案和49份公钥加密或密钥封装方案[15]。经过第1轮评估，有26个候选方案进入了第2轮评估，包括17份公钥加密或密钥封装方案和9份数字签名方案[16]，其中12份加密方案是基于格的PQC方案，占据了所有加密方案的一半。

在2020年10月，NIST公布了第3轮征集的密码方案[17]，具体方案如表2所示。其中，CRYSTALS-KYBER，NTRU和SABER是基于格的公钥加密或密钥封装方案，CRYSTALS-Dilithium和FALCON是基于格的数字签名方案。基于格的加密体制成为了最有可能PQC标准化的方案。

表2 NIST第3轮提交算法Tab.2 Submitted algorithms in NIST round 3

NIST预计在2024年之前完成对PQC最终入选算法的标准制定，公布PQC的标准化草案。届时，新的密码体系将取代现有的密码体系，来应对日益突出的量子威胁，为保密信息、数字签名和信息访问等应用保证其安全性和授权控制。

2 基于格的几种PQC算法

2.1 Saber算法

Saber算法是一种基于格的密钥封装机制(KEM)算法，在安全性级别的发展上，首先是一个基于2个模p和q的幂的选择明文攻击(Chosen Plaintext Attack，CPA)的安全公钥加密(PKE)方案，然后经过Fujisaki-Okamoto的改造为随机选择密文攻击(IND-CCA)安全的KEM[18]。其安全性基于带舍入的学习(Learning-with-Rounding，LWR)的变体MLWR，MLWR问题是基于模块矩阵的LWR问题。LWR是LWE问题的一种变体，其中误差项是通过舍入操作引入的，而不是从随机分布中获得的。

Saber通过不同参数的设置决定了Saber的不同安全级别，但是三者的多项式的次数N都为256，模q=213，p=210，具体如表3所示。

表3 Saber算法的不同分支Tab.3 Different branches of Saber algorithm

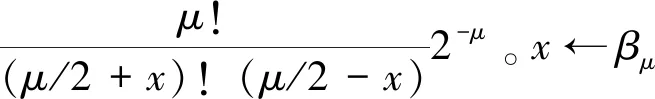
Saber公钥加密方案包括3个阶段：密钥生成、加密和解密。

算法1:Saber密钥生成输入:种子 (0,1)256,常数向量h输出:公钥pk,私钥sk1.从 (0,1)256均匀生成l×l阶多项式矩阵A,A=gen(seedA)∈ l×lp2.均匀生成r= ({0,1}256),从二项分布中随机生成s=βμ( l×1q;r)3.缩放生成向量b,b=((ATs+h)modq)4.对向量b舍入,b≫(εq-εp)∈ l×1p5.得到公钥pk,pk=(seedA,b)6.对pk进行哈希变换,pkh= (pk)7.均匀生成向量z1= ({0,1}256)8.得到私钥sk,sk=(s,z1,pkh)

在密钥生成阶段中，函数gen是基于SHAKE-128的伪随机数生成器，用于从种子中获取矩阵，生成了多项式的公共矩阵A和多项式的秘密向量s。同时，对乘积As进行缩放和舍入得到向量b，其中公钥由A和b组成，密钥为向量s。

算法2:Saber加密操作输入:公钥pk,种子 (0,1)256,向量r输出:密文c,共享密钥K1.均匀选取生成消息m= ({0,1}256)2.如果r未被指定,则均匀生成r= ({0,1}256)3.从二项分布中随机生成s′=βμ( l×1q;r)4.缩放生成向量b′,b′=((As′+h)modq)5.对向量b′舍入,b′≫(εq-εp)∈ l×1p6.加密向量v′1=bT(s′modp)∈ p7.缩放生成cm,cm=(v′1+h1-2εp-1mmodp)8.对向量cm舍入,cm≫(εp-εT)∈ T9.得到密文c=(cm,b′)10.通过哈希函数生成(K^,c)= (F(pk),m)11.通过哈希函数生成K= (K^,c)

在加密阶段中，消息由v′1=s′bT(s′是专门为加密生成的向量)加密。生成的密文涉及到向量b′，b′由As′产生。

算法3:Saber解密操作输入:公钥pk,私钥sk,密文c,向量z1输出:共享密钥K1.解密向量v1=b′T(smodp)∈ p2.解密生成原文消息m′,缩放m′=((v1-2εp-εTcm+b2)modp)舍入m′≫(εp-1)∈ 23.调用加密操作生成m′的密文c′4.如果c=c′,则返回共享密钥K= (K^,c)5.否则返回共享密钥K= (z1,c)

在解密阶段中，通过来自sb′的v1的近似来恢复消息，然后再加密与已有的密文消息对比，如果相同，则接受，否则拒绝。

2.2 CRYSTALS-KYBER算法

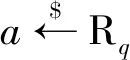
数论变换(Number Theoretic Transform，NTT)操作将传统的多项式乘法运算转化为系数式乘法运算，降低了多项式乘法运算的复杂度。INTT操作是NTT操作的逆操作，将系数式乘法运算转化回多项式乘法运算。CWM算法是将2个二次多项式在q[x]/(x2-ωi)中相乘，其中i随系数的指标变化[20]。

Kyber是由公钥加密方案转化而来的KEM，是NIST后量子标准中提出的算法。Kyber算法适用于多项式环Rq，其中φ(x),q,n分别为xn+1，3 329，256。Kyber算法的密钥生成、加密和解密操作如下。

算法4:Kyber密钥生成输入:字节数组(0,1)256输出:公钥pk,私钥sk1.从Rk×kq中均匀采样生成多项式矩阵A-2.从Rkq中中心二项分布采样生成向量s,e3.公钥pk=A-s+e4.均匀生成32位字节数组z5.私钥sk=(s,pk, (pk),z)

密钥生成操作需要2k次NTT操作和k2次系数式乘法运算(CWM)操作。

算法5:Kyber加密操作输入:公钥pk,消息m输出:密文c,共享密钥K1.消息m是均匀生成的32位字节数组2.m= (m)3.(K-,r)= (m, (pk))4.从Rk×kq中均匀采样生成多项式矩阵A-5.中心二项分布采样生成向量r,e1←＄Rkq6.中心二项分布采样生成向量e2←＄Rq7.计算u=ATr+e18.生成密文c,c=(u,v)=(ATr+e1,pkTr+e2+m)9.共享密钥K=(K-, (c))

加密操作需要k次NTT，k2+k次CWM和k+1次INTT操作。

算法6:Kyber解密操作输入:私钥sk,密文c,向量z输出:共享密钥K1.解密生成原文消息m′,m′=v-skTu2.加密操作的常数向量h3.哈希变换得到(K-′,r′)= (m′,h)4.利用加密操作生成m′的密文c′5.如果c=c′,则返回共享密钥K=(K-′, (c))6.否则返回共享密钥K=(z, (c))

Kyber算法中k取值为{2,3,4}，通过改变参数k可以调整其安全级别。

2.3 CRYSTALS-Dilithium算法

CRYSTALS-Dilithium是NIST第3轮后量子数字签名候选方案中的一种，是一种基于晶格的数字签名方案，属于代数格加密套件(CRYSTALS)及密钥封装机制中的一种。Dilithium算法的核心运算是多项式矩阵和向量的运算，安全性基于模块化带错误学习(M-LWE)和最短整数解(SIS)问题，但是不同的是所有多项式的采样都是均匀采样，多项式的生成比较简约[21]。Dilithium算法中n=256，q=223-213+1。Dilithium数字签名方案的安全级别可通过表4中的参数进行调整。

表4 Dilithium算法不同安全级别下的参数设置Tab.4 Parameter settings of Dilithium algorithm at different security levels

Dilithium数字签名方案的3个核心算法是密钥生成、签名生成和签名验证，具体算法如下。

算法7:Dilithium密钥生成输入:种子ζ∈{0,1}256输出:公钥pk和私钥sk1.从多项式环Rq均匀生成k×ℓ阶多项式矩阵A∈ k×lp2.从多项式环Rq均匀生成多项式向量s1和s23.计算t=As1+s24.将t拆解为t=t0+bt15.生成公钥pk=(A,t1)6.生成私钥sk=(A,t0,s1,s2)

在Dilithium数字签名方案的密钥生成中，为了保持公钥大小较小，矩阵A被种子ρ替换，种子ρ生成确定性密钥，这是基于晶格的密码学中广泛使用的技术。此外，将t中每个系数的较低d位放在密钥中，来进一步降低公钥大小。

算法8:Dilithium签名生成输入:私钥sk,消息M∈{0,1}∗,常数向量h输出:三元组 σ=(z,h,c)1.初始化(z,h)为无效2.当(z,h)无效时执行循环3.生成隐蔽向量y←Sℓγ14.计算w=Ay,使w=w1·2γ2+w05.c=哈希(M‖w1)∈Bτ,使多项式c的τ个系数为±1,其他系数为06.生成潜在签名z=y+cs17.w-cs2=w2·2γ2+w38.如果‖z‖∞≥γ1-β或者‖w2‖∞≥γ2-β 则返回(z,h)无效9.否则计算由t中的未知部分产生的进位向量h,h由-ct0和w-cs2+ct0的高位产生10.如果‖ct0‖∞≥γ2或者h≥ω则11.返回(z,h)无效12.结束循环

在签名生成中，签名算法选择一个掩蔽向量y，其中的系数来自[-γ1,γ1)，来计算后续w=Ay。检查多项式的最大范数是否在可接受的预定义范围和向量的最大范数，来检查签名是否泄漏有关该秘密值的信息。额外增加的一个拒绝条件是提示h验证算法期间t的哪些系数需要进位。根据安全级别的不同，平均需要尝试3～5次才能生成有效的签名。

算法9:Dilithium签名验证输入:公钥pk,消息M∈{0,1}∗,三元组σ=(z,h,c)输出:有效或无效1.Az-ct1结果的四舍五入的高位为w′1,w′1=(h,Az-ct1·2d,2γ2)2.如果‖z‖∞<γ1-β且c= (M‖w′1) 且h≤ω,则返回有效3.否则返回无效

在签名验证过程中，由于t中每个系数的低位不包含在公钥中，因此验证器利用提示h来执行该操作。随后，根据消息和w′1重新计算质询c，并将其与签名中提供的质询c进行比较。此外，检查z是否具有有效范数(即每个系数是否具有签名生成期间检查的最大值)。

3 硬件实现

目前，对于基于格的密码体制的高效硬件实现是当期研究的热点，大量的研究者们不但提出了PQC方案，也提供了硬件上实现的结果。格基密码体制易于在硬件中高效实现，主要优势在于格基密码体制中的运算主要是多项式计算，可以利用NTT算法实现高效快速乘法，在硬件中极大地提高了格基密码方案的吞吐量[22]。同时，硬件实现相比于软件有着高效并行处理的优势，加速处理多项式中的复杂计算，而且性能与资源上的权衡十分出色，应用场景广泛。

硬件上的开发方法主要可以分为软硬件协同设计(RTL)和高级综合(High Level Synthesis，HLS)2种方法，在硬件上的实现平台主要有Xilinx FPGA上的Virtex-7，UltraScale+和Artix-7等平台，完成对格基密码体制的硬件实现。

3.1 Saber算法的硬件实现

Saber算法是NIST第3轮评估中的候选算法之一，研究者们对于Saber算法在硬件上的实现的研究很多。Roy等人[23]设计了一个指令集协处理器架构，可以提供指令级的灵活性和模块化，易于添加或修改新的指令。在多项式的乘法优化上，对绝对值进行乘法运算，然后累加器通过系数符号位决定是加法还是减法，这样将乘法转化为移位和相加操作，优化了架构，减少周期、逻辑和寄存器数量，具体的多项式乘法器结构如图1所示。同时，乘法器是大规模并行的，不会受到内存访问瓶颈的影响。多项式的结构易于扩展，可以满足不同性能的需求，支持Saber算法的几种变体。

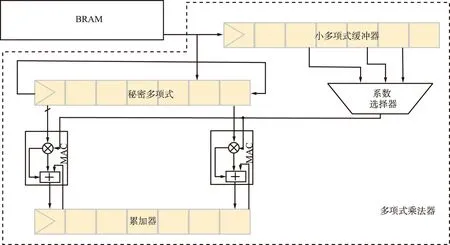
图1 多项式乘法器结构Fig.1 Polynomial multiplier structure

文献[24]基于多项式乘法产生的乘法输出是并行的，但需要的输出是串行的问题，提出了一种新的循环面向行处理(CROP)策略，把乘法器的输出放到下一个寄存器中存储，进行N步后，把所有寄存器中的输出进行循环累积，进而很容易地实现串行操作。具体来说，把N步操作拆为了r×t步，即每个t子累积需要r步循环，从而更高速地实现多项式乘法的输出操作。使用了2个移位寄存器(SR)和N个处理元件(PE)，实现了CROP策略在硬件上的实现。

Zhu等人[25]对之前的分层Karatsuba框架进行了优化，之前的这一框架实现了多项式乘法的分步操作，分为了预加、乘法和后加3步，但是没有考虑输入端加法器和寄存器的复用。通过调度层实现了寄存器和加法器的重用，资源上节约了90%。同时，权衡了调度层和内核层，使得预加和后加操作变得更加紧凑，均衡了计算速度和延迟面积。Saber算法中的多项式可以通过流水线方式生成，且与乘法硬件并行生成，减少了延迟开销和多项式的内存。同时，引入了截断乘子来实现细粒度处理。

多项式乘法时，一个多项式的系数较小(-4～+4)，另一个多项式的系数为10位或13位。因此，Basso等人[26]采取集中式乘法器结构，使用预计算的方法，把乘法结果预先计算好，这样MAC内部的乘法变成了简单的选择操作，显著减少了MAC单元的面积。数字信号处理模块(DSP)负责处理这种系数乘法，一个DSP包含2个公共多项式系数和2个秘密系数，一个DSP就可以计算4个系数乘法，通过128组DSP可以实现128个周期内计算256系数多项式的乘法。通过使用多路复用器(MUX)将多项式乘法的并行输出变为串行输出存储到外存中。

He等人[27]通过可伸缩矩阵源处理(SMOP)，把多项式乘法中的系数相乘转换为矩阵形式。建立了一套完整的体系结构，将算术运算与信号控制流均集成到硬件上，得到紧凑的协处理器结构。整个系统包括数据流和控制流，其中重点的多项式乘法部分，将SMOP的算法做到硬件上，通过循环移位寄存器(CSR)、乘法和加法器(MAA)和累加器(AC)来实现多项式乘法和并行输入串行输出(PISO)。He等人还展示了2个或4个CSR分组下，整个处理器的不同流程。这些实验的具体对比如表5所示[23-27]，Saber算法为标准的Saber算法。

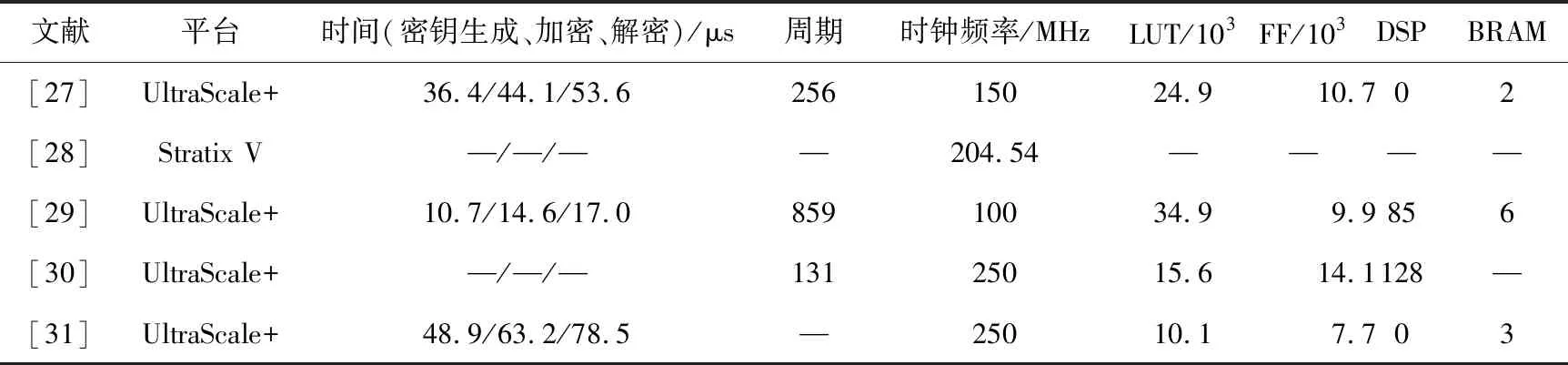
表5 Saber算法硬件实现的对比Tab.5 Comparison of Saber algorithm hardware implementation

Xie等人的设计与Basso等人的设计相比，在性能无差距下，设计的面积延迟积(ADP)降低了10%。

从表5中可以看到，Zhu等人针对分层Karatsuba框架的优化，在性能上的表现最好，但是其需要的资源也最多，尤其是DSP和BRAM，因此，比较适合追求性能不注重成本的应用场合。He等人的可伸缩矩阵源处理需要的硬件资源最少，因此性能表现较差，适合轻量化的场景。Roy等人对多项式乘法器进行优化，将乘法转化为移位和相加操作，在综合的性能和资源上的表现最优。

3.2 CRYSTALS-KYBER算法的硬件实现

KYBER体系结构分为3个主要核心：Keccak(哈希和采样)、NTT和Control(控制器和所有其他所需函数)。Huang等人[28]发现在算法的整体阶段中，尤其是加密和解密阶段，存在很多可以重复使用的单元，且加密和解密过程一般并不冲突，可以复用这些单元来节省硬件成本。因此，他们将所有哈希函数集成为一个哈希模块，同时引入BRAM来存储中间数据，尽可能地利用FPGA，在一个时钟周期内实现Keccak置换过程。在使用Montgomery Reduction时，其中的3次乘法和1次减法，通过在硬件中使用流水线的方法，算法的时钟周期变为原来的1/4。

Bisheh-Niasar等人[29]利用KRED和KRED-2X算法来实现多项式的模化约减，且只需要移位和加法操作，但是只能输出16位数据，为了输出32位数据，提出了K2-RED算法，减少了移位和加法操作，且12位的输出也意味着占用的内存更少。为了避免多项式乘法中的位反转成本，提出了2×2的可重构蝶形结构，支持CT和GS操作，来合并2层NTT，且每层执行2个蝶形操作，减少硬件资源。

Yarman等人[30]在模约减单元采用了滑动递归的方法，组合相同的位来消除冗余操作，同时简化操作，实现了一个时钟周期的延迟。设计的蝶形单元可以用于NTT和INTT操作，每个蝶形单元包括4个双端口的BRAM，其中2个BRAM存储第1个输入多项式和输出多项式，另外2个存储第2个输入多项式，同时还拥有一个BROM，用于存储预计算和加载的旋转因子幂，通过多路复用器进行多项式的传输操作。还设计了轻量级、平衡和高性能的硬件架构，分别使用1个、4个和16个蝶形单元，来应对不同的使用场景。

Xing等人[31]实现了CRYSTALS-KYBER算法的纯手动设计硬件，不需要借助ARM Cortex等硬连线处理器和RISC-V等可重构逻辑。系统中设计使用了2个蝶形单元，分别用于处理KYBER中的一个256项NTT，NTT分解为2个独立的偶数索引和奇数索引，具体的NTT操作(上方)和INTT操作(下方)如图2所示。

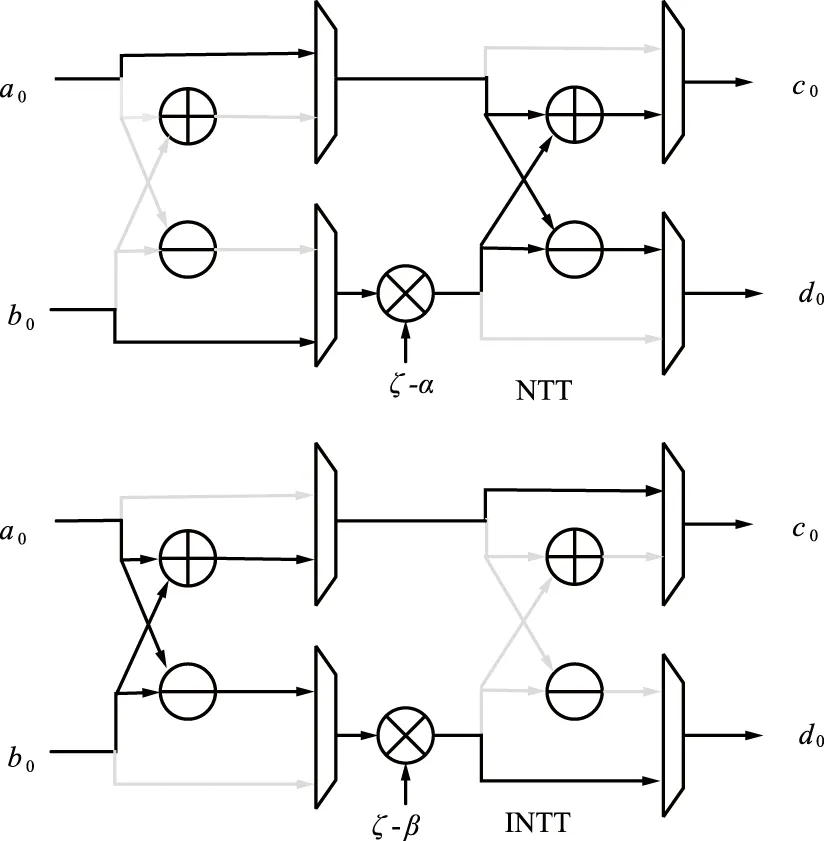
图2 NTT和INTT中的蝶形单元Fig.2 Butterfly units in NTT and INTT

在逐点乘法中，采用了Karatsuba算法，降低了乘法操作的次数。同时,使用Barrett的模约减操作降低了DSP等资源的消耗。将减少系统资源消耗的关键放在了内存占用上，主要包括数据在RAM上的即时存储、解决读写速率不匹配而灵活多变的FIFO存储器以及重新加密阶段充分利用FIFO存储器等方法。这些实验的具体对比如表6所示[28-31]，KYBER算法为Kyber-512。

表6 KYBER算法硬件实现的对比Tab.6 Comparison of hardware implementation of Kyber algorithm

从表6中可以看出，Xing等人的纯手动设计硬件实现，由于不需要ARM Cortex等硬连线处理器和RISC-V等可重构逻辑，因此在综合的性能与资源上的表现最为优秀。Bisheh-Niasar等人提出的K2-RED算法从算法层次减少了移位和加法操作，根本上降低了硬件上的资源使用。

3.3 CRYSTALS-Dilithium算法的硬件实现

Beckwith等人[32]实现了对Dilithium的不同安全级别下不同的相关参数的高性能硬件实现，算法中很多操作存在大量的数据依赖性，使得通过高度并行化来提升效率变得很难。提高性能的方向主要是优化多项式运算单元和优化操作调度。在多项式运算单元上，使用了2×2的蝶形单元、地址解析单元和FIFO存储器，一次处理2层来降低NTT中的内存访问成本，同时也不会占用过多的资源。Dilithium算法中的多项式采样需要大量的伪随机数据，使用了3个Keccak核，为向量和矩阵添加了多条拒绝通道，并行处理伪随机数据，提升了吞吐量。在优化操作调度上，将签名生成单元中的拒绝循环拆分为2级管道，加速单个操作的性能来加速整体的性能。

Land等人[33]利用DSP模块中的动态配置、预加法和单指令多数据(SIMD)的功能实现了NTT，MACC等所有的具体功能模块，减少了内存占用，省去了多项式重新采样，模块间又执行流水线处理，加快了算法实现。在NTT模块中，之前的NTT结构一般只使用DSP进行低延迟乘法，充分利用了DSP中的移位寄存器、多路复用器等单元，通过预计算蝶形单元中的旋转因子，加快了INTT操作，给NTT等所有相关的算术操作都实现了低延迟。这里同样使用BRAM来存储多项式，不同的是系数存放的间接地址，使读写冲突的数量降到了最低。在模约简模块中，利用模运算的数学关系对46位值的s进行了简化。整个架构的算术操作由NTT，MACC和矩阵向量乘法执行，检查模块会对多项式的范数进行检查，采样模块和Keccak模块负责多项式的随机生成，共同受控制单元的调度。

Ricci等人[34]用VHDL语言设计和实现了Dilithium算法中的所有底层功能，包括SHAKE-128，SHAKE-256，NTT和ExpandAq等函数，而且针对硬件环境对这些函数做了进一步的优化，然后将这些函数集成到了Dilithium算法的密钥生成、签名和验证3个阶段，来提升算法的处理速度。

Zhao等人[35]提出了一种分段流水线处理方法，将算法中的操作分成多个段，硬件以流水线方式一次处理一个段。这种方法大大减少了中间结果的存储需求，并隐藏了许多操作的执行时间。优化模块，包括高速流水线NTT模块、基于BRAM的采样模块、紧凑分解模块和3个定制的模块化简模块。整体的系统结构如图3所示。

图3 系统结构Fig.3 System structure diagram

本文将整个系统分为了NTT、头部、尾部等多个模块组件，因此采用了分段流水线的处理方法，将数字签名算法中的操作分为多个段，以流水线的方式一次处理一个段，每段通过对应模块分别执行多项式生成和采样以及NTT操作，大大减少了中间结果的存储需求，并隐藏了许多操作的执行时间。根据模数q和BRAM的位宽关系，将3个阵列为一组存储多项式的4个系数，提高BRAM存储空间的利用率。同时，多项式矩阵是实时计算，而非预先计算，从而避免在BRAM中的无效存储。通过利用BRAM的空闲区域，来替换移位寄存器，折叠变换蝶形单元，提高了资源利用率，优化了NTT模块。

这些实验的具体对比如表7所示[32-35]，Dilithium算法为安全级别2下的算法。

表7 Dilithium算法硬件实现的对比Tab.7 Comparison of hardware implementation of Dilithium algorithm

Ricci等人使用VHDL语言重新设计了所有底层功能，极大地降低了Dilithium算法的密钥生成、签名和验证时间，但是占用的资源也极多。Zhao等人提出的分段流水线处理，一方面极大地降低了资源消耗，同时时间上表现的差距不大，综合性能表现上最好。

4 侧信道攻击分析

格基密码体制通过格中难解数学问题保证了其算法的安全性，但是硬件的具体实现往往会面临侧信道攻击，进而影响算法的安全性和性能[36]，例如芯片的瞬时功耗，以提取由实现处理的密钥[37]。侧信道攻击一般通过检测目标设备泄露的物理信息进行分析，如执行算法每一步时需要的时间或者功率轨迹、消耗的能量、发射的电磁波和产生的错误输出等，从而提取出算法的密钥。典型的侧信道攻击分为冷启动攻击[38]、故障攻击[39]、定时攻击[40]和功率分析[41]等。因此，需要对这些格基密码算法对侧信道攻击进行分析，从而找到解决对策。

物理安全性有限或没有物理安全性的轻量级应用程序更容易受到此类攻击，因为对手可以轻松收集旁道信息。不同平台的泄漏模式不同。例如，源于处理器架构的泄漏可能会影响软件，而依赖于基本组合和时序电路构建块的小故障会影响硬件实现。针对基于晶格密码体制的第1种侧通道攻击是对NTRUEncrypt实现的定时攻击[42]，该攻击利用的是解密过程中哈希函数的执行时间取决于密文这一过程。

在Saber算法去封装的过程中，一般会长期使用私钥，这会导致容易受到侧信道分析，解决这一问题的方法是对密钥操作进行隐藏处理。有效的掩模设计分为2个模的幂和舍入学习的有限噪声采样，面临的主要挑战是将逐位运算与算术掩蔽相结合，要求算法在掩蔽表示之间进行安全转换。所描述的设计包括一个用于算术共享上的屏蔽逻辑移位的新原语，以及对现有的Saber屏蔽二项式采样器进行调整。

Abdulgadir等人[43]采用寄存器—传输层(RTL)的方法来构建硬件，对使用私钥操作的每一单元都进行了隐藏处理。在多项式运算单元上，将多项式生成为2个多项式，使得乘积为另一个多项式与这2个多项式乘积的和。在SHA3单元，使用不相关的状态来提供非线性运算所需的随机性。中心二项分布(CBD)取样器单元上，使用了Goubin布尔型转向算术型的方法，转换采样中的几位。同时，还设计了高效的屏蔽逻辑移位单元方法实现了逻辑移位单元的隐藏。实验表明，抗CSA攻击下，系统使用的LUT和延迟分别是不抗CSA攻击的2.9倍和1.4倍。

对于CRYSTALS-KYBER算法的抗侧信道攻击防护，Jati等人[44]在整体的硬件架构上使用了广泛的资源共享，包括算术运算、控制信号及FSM，同时实现了更小的SHA-3内核，LUT和FF的数量减少了70%和50%，在具有高性能的同时有着最小的开销，同时提供了良好的抗故障性。实现抗侧信道攻击的策略有3种：随机延迟，由基于TRNG的环形振荡器的真随机数生成器生成；地址随机化，在系统启动/重置时使用随机数据和fisher-yates-shuffle技术[45]创建的地址随机化，在每条指令结束后随机更新排列；指令随机化，引入一条名为INSTRND的指令使接下来的N条指令以随机顺序执行。同时，设计了一种基于替代置换网络(SPN)结构的良好微分偏差的16×8哈希来保护指令指针和内存。

Karabulut等人[46]发现CRYSTALS-Dilitium算法中的ω-小多项式采样过程会泄漏有关系数的-1，0或+1赋值的信息，进一步证明，这一采样过程可以在单个功率测量中找到，并且可以恢复会话密钥，针对这一问题的攻击恢复系数符号的成功率超过99.99%，将被拒绝的挑战多项式的熵降低到39～60位。

Chen等人[47]针对CRYSTALS-Dilithium算法提出了一个保守的方案和一个快速的两阶段攻击策略。对手可以将这2种方案结合起来，通过高效的混合CPA(相关功率分析)攻击，可以分析出p的最低有效位，进而恢复相关候选序列，恢复完整的秘密系数。实验表明，在合理的功率跟踪量下，该算法的置信度可达99.99%。得益于这一策略，对手可以以7.77倍的加速度恢复密钥。这项工作指出，基于非保护NTT的多项式乘法是脆弱的。

针对不同类型的攻击和不同应用应当采取不同的对策，对于轻量级的硬件实现，这些设备往往布置在受约束的环境和移动设备上，攻击者的攻击一般是在设备的正常操作期间进行攻击，因此，主要需要进行电磁攻击的额外防护。而在其他任何嵌入式的设备当中，尤其是针对多个用户共享的平台，需要防止缓存泄露。大多数的PQC算法仍在开发和实验验证阶段，实验框架一直处于大量修改和扩展阶段，提出的一些针对侧信道攻击的防御对策往往只使用于特定算法，具有局限性。

5 结束语

通过对Saber算法、CRYSTALS-KYBER算法和CRYSTALS-Dilithium算法的详细算法介绍和相关的硬件实现介绍，展示了格基量子密码学相关的背景、基础知识和发展现状。着重介绍了格基密码的硬件实现部分，对于算法中的多项式采样模块和多项式乘法模块的具体实现进行了总结分析，尤其是NTT算法在多项式乘法器模块中的应用，通过蝶形单元大大降低了NTT操作时间，借由实验数据对比展现了不同改进型密码系统的架构和优劣。最后，对硬件实现中可能面临的侧信道攻击进行了总结分析，介绍了抗侧信道攻击的硬件设计思路。

在后量子时代，基于格的PQC体制以其强大的安全性、平衡性和灵活性成为了PQC学中最为活跃的部分，其与硬件的高效结合充分展示了其灵活性和广阔的实用场景，推动着密码学与实际应用的不断结合。