信息物理系统中基于能量效率的干扰策略优化
甘瑞蒙,王洋洋,肖 哲,杜 丹,焦利彬
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.通信网信息传输与分发技术重点实验室,河北 石家庄 050081;3.陆军装备部驻石家庄地区第一军代室,河北 石家庄 050081)
0 引言
信息物理系统(Cyber-Physical System,CPS)是由信息系统、物理系统通过通信网络无缝连接的高度复杂系统,在智能电网[1]、无人机[2]和智能医疗[3]等方面具有潜在的应用价值。2007年,美国将CPS视为未来8项网络与信息技术之首;2013年,德国将其列为“工业4.0”之首;我国将CPS视为支撑新一轮产业变革的核心技术,并在《信息物理系统白皮书(2017)》中提出CPS是通过集成先进的感知、计算、通信、控制等信息技术和自动控制技术,构建物理空间与信息空间中人、机、物、环境、信息等要素相互映射、适时交互、高效协同的复杂系统,实现系统内资源配置和运行的按需响应、快速迭代、动态优化[4]。通常,由于无线传感器成本低、布置灵活等特点,在CPS中会采用无线传感器感知数据并将此数据通过无线信道发送到远端状态估计器。在数据传输过程中,不同类型的网络袭击会在不同程度上恶化CPS的性能,甚至导致系统崩溃,因此,为了保障数据传输的有效性,对CPS的安全性问题进行研究是十分必要的。
目前,对CPS安全性问题的研究主要集中在以下三方面:一是从被干扰者角度出发研究如何设计最优的抗干扰策略或者增强系统本身的抗干扰能力。例如,文献[5]在多信道受到拒绝服务(Denial-of-Service,DoS)袭击时,为CPS中基于分布式事件驱动的远程状态估计问题设计出一种基于观测的事件驱动策略以提高系统的传输效率;文献[6]为非线性反馈系统提出一种基于多观测和切换的机制,以维持CPS的远程状态估计性能。二是同时从被干扰者和干扰者角度出发,应用博弈论理论设计均衡策略。例如,假设传感器和DoS干扰机在每个传输时刻所用能量有限,在多信道数据传输条件下,文献[7]为传感器和具有相反目标的DoS干扰机设计出一种基于零和博弈的均衡策略;假设有限时间内传感器在节省能量的同时旨在通过信道的局部选择最小化系统误差,而具有相反目标的DoS干扰机通过选择是否进行信道干扰恶化系统性能;文献[8]为二者设计出基于分布式强化学习的均衡策略。三是从干扰者角度出发研究如何设计最优的干扰策略,从而最大程度地降低CPS的性能。例如,对于能量有限且干扰次数有限的DoS干扰机,文献[9]研究了干扰机何时进行干扰才能最大化远程状态估计误差的问题;假设DoS干扰机每次只能选择部分信道进行干扰,文献[10]为含有多个子系统的CPS提出了基于马尔科夫决策过程(Markov Decision Process,MDP)的最优干扰策略;假设干扰机每次只能干扰一条信道,在含有2个传感器的CPS中,文献[11]提出了一种最大化平均估计误差的最优干扰策略。
上述关于最优干扰策略设计的研究都是假设传感器有足够的能量,能够将观测数据通过无线信道直接发送到远端的估计器。实际上,无线传感器通常所含能量有限,导致其传输范围有限从而不能将数据直接发送到远端估计器,此时无线传感器需要通过中继协助才能将观测数据发送到远端估计器。在基于多传感器的远程状态估计问题中,文献[12]根据中继能力的不同分别设计了直接转发策略和局部处理再转发策略;假设干扰次数有限,且每次只能干扰一个信道,文献[13]基于MDP提出了一种最优化终端估计误差的动态DoS干扰策略。
此外,能量效率最大化问题在无线通信网络中受到了普遍的关注,例如,文献[14]在无线能量采集传感器网络中研究了基于吞吐量的能量效率问题;文献[15]基于频谱利用率研究了认知M2M网络中的频谱效率问题。本文从干扰机角度出发,研究在协作通信时如何设计DoS干扰机的袭击策略,从而最大化CPS中基于估计误差的能量效率问题。本文的主要贡献概括如下:
① 研究了协作通信的CPS中DoS干扰机如何通过信道选择和能量分配最大化能量效率的问题,建立了对应的基于终端估计误差的混合整数规划模型。
② 通过列出目标函数的显性表达式,提出了获得最优干扰策略的必要条件,并基于此必要条件给出最优干扰策略算法。
1 远程状态估计及干扰模型
基于中继的两跳远程状态估计结构如图1所示,其中传感器、中继和远程估计器分别用符号R0,R1和R2表示;传感器与中继之间、中继和估计器之间的信道分别用C1和C2表示。

图1 远程状态估计结构示意Fig.1 Structure schematic diagram of remote state estimation
物理过程采用基于离散时间域上的线性时不变系统来描述:
(1)
式中,xt∈nx为物理系统在时刻t的状态;ωt∈nx为物理系统更新时的噪声,服从高斯分布N(0,Σω),且是稳定的[16]。
传感器使用线性时不变系统对图1中的物理过程进行采样观察:
(2)
式中,yt∈ny为测量结果;νt∈ny为测量噪声且服从高斯分布N(0,Σν)。此外,通常假定(A,C)是可观测的。
传感器R0将观测到的数据通过中继R1发送给估计器R2,在此期间,干扰机会干扰无线信道C1或信道C2以降低系统的性能。对于能量有限的干扰机,主要问题是如何通过选择信道和调度有限的能量最大化干扰效果。
1.1 协作通信模型
假定传感器R0能量有限,且估计器R2位于传感器R0的传输范围之外,即传感器R0和估计器R2不能直接进行数据传输。在收发两端配置中继是解决此类由于发端能量有限而不能直接将数据传输到终端问题的一种有效方法[13]。基于对接收到的数据处理方式的不同,中继通常分为以下2种类型:一是将接收到的数据直接转发给下一个节点;二是在转发接收到的数据之前首先对接收到的数据进行局部处理,中继根据自身的配置能力选择用哪一种方式处理接收到数据[12]。对于任意的i=1,2,本文假定Ri只能接收Ri-1发送的数据,且中继有足够的能力对数据执行局部估计。
此外,由于信道本身的特性,在无线网络中有可能发生丢包的现象,即Ri有可能接收不到Ri-1发送的数据。用丢包率αi刻画Ri接收Ri-1发送数据的情况,且将丢包率看作是信噪比的函数[9],有:
(3)
式中,f(x)是x的单调非增函数,且
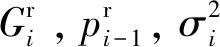
(4)

(5)
(6)
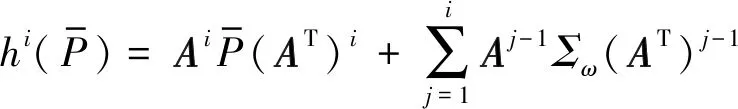
1.2 干扰模型
基于不同的干扰目标,干扰机可以分为3种类型:一是注入式干扰,即干扰传输数据本身;二是DoS干扰,干扰机的目的是阻碍数据传输而不改变正在传输的数据;三是窃听干扰,干扰机不干涉数据本身和其对应的传输信道,只是窃听传输的数据。本文假设干扰机配置DoS袭击设备,即通过干扰无线传输信道降低CPS系统性能。
(7)
式中,
2 问题建模
通常,远程估计器R2通过计算估计误差来反映物理系统状态,因此终端估计误差[17]是衡量远程状态估计的一个重要指标:
(8)
式中,N为总的干扰次数。
作为对立面,干扰机的目的是在节省能量的同时最大化终端估计误差fN降低干扰期间CPS的性能。当每次只能干扰一条信道时,对于图1所示的通信拓扑,干扰机面临的问题是选择哪条信道进行干扰以达到干扰目的。对于任意的i=1,2,令xi∈{0,1}为示性函数,其中xi=1表示干扰机干扰信道Ci,否则xi=0。那么,干扰机通过解决优化问题:
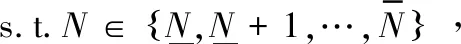
(9)
(10)
(11)
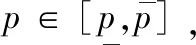
(12)
此优化问题属于混合整数规划问题,通常很难得到解析解,因此本文通过对优化问题的分析得到求解最优干扰策略的数值解。
3 最优干扰策略
首先分析优化问题P1中目标函数的显性表达式,然后得到最优解的必要条件,最后提出求解最优干扰策略的算法。
3.1 最优干扰策略分析
由式(3)~式(5)可知,每个信道的丢包率除了受本身通信环境的约束,还受干扰机是否进行干扰的影响。令γi表示干扰机进行信道选择时信道Ci的丢包率,则对任意的i=1,2,有:
(13)
成立。假设在整个干扰期间,干扰机只选择其中一个相同的信道进行干扰,那么,对于任意的t∈{1,2,…,N},信道Ci的丢包率可以用γi表示。

(14)
远程状态估计器R2处的估计误差为:
(15)
进一步,由式(14)和式(15)可得R2处估计误差的概率密度函数为:
(16)

因此,优化问题P1中的目标函数可以表示为:
(17)

干扰信道确定后,对于任意给定的干扰次数N,优化问题P1可以简化为只含连续变量的优化问题P2:
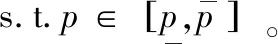
(18)

(19)
由式(19)得:
(20)
进一步,由式(12)和式(20)可知,优化问题P2获得最优解的必要条件为:
(21)
式中,
即优化问题P2获得最优解的必要条件为能量效率对每个信道的能量增量一样。
3.2 最优干扰策略算法
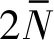

算法 EEOAS输入:系统(1)与(2)中的参数:A,C,Σω,Σv;信道参数:Gri,pri-1,Gai,pai,σ2i;N,N-。输出:信道选择xi,对应的最优干扰次数N∗与能量p∗(N∗)。初始化:S1=S2=0;1.fori=1,22.forj=N,…,N-3.根据式(21)计算最优的能量p∗i(Nji);4.根据式(8)计算fNjiNjip∗(Nji);5.iffNjiNjip∗(Nji)≥Si6.N∗=Nji;7.end if8.end for9.ifS1-S2>010.x1=1;11.else12.x2=1;11.end if
4 实验与分析
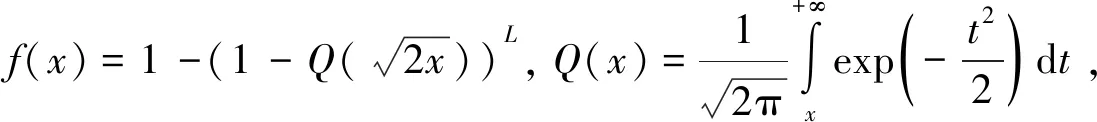
干扰能量及信道选择对能量效率的影响如图2所示。
由图2可以看出,对于相同的信道,不同的干扰能量对应不同的能量效率,且不同的干扰次数对应的能量效率也不一样,即干扰次数、干扰能量及所干扰信道都会对能量效率产生影响;当所用能量一样时,不同的干扰次数以及干扰不同的信道所产生的能量效率也是不一样的。因此,为了最大化干扰机的能量效率,有必要选择最优的干扰信道及相应的干扰能量。任意给定干扰次数对应能量效率最大化的干扰能量如表1所示。

图2 干扰能量及信道选择对能量效率的影响Fig.2 Effect of energy jamming and channel selection on energy efficiency

表1 固定干扰次数对应的最优干扰能量Tab.1 Optimal jamming energy for fixed number of attacks
不同干扰策略对干扰效率的影响如图3所示。平均策略所用的干扰能量为干扰机能量上限的中值,随机策略为在有限能量范围内随机选择,最大策略为使用干扰机的最大能量。由图3可以看出,对于任意给定的干扰次数,本文所提EEOAS算法获得的能量效率要优于其他3种策略,说明本文算法的有效性;当N≥3时,对于EEOAS算法,能量效率随着干扰次数的增加而逐渐提高。
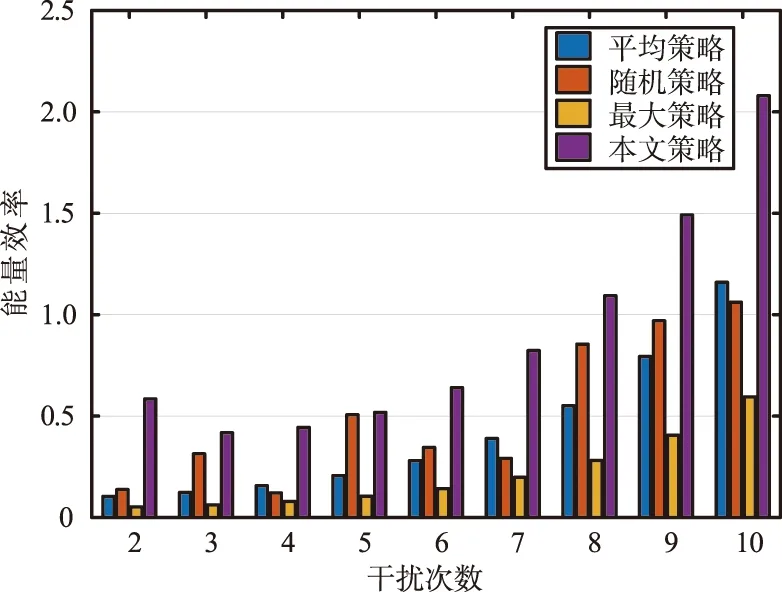
图3 不同干扰策略对干扰效率的影响Fig.3 Effect of different jamming strategies on jamming efficiency
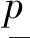
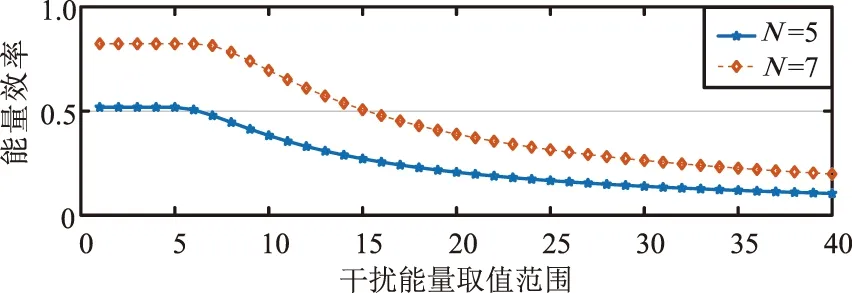
(a) 干扰能量下界变化
5 结束语
本文主要研究了CPS中的安全性问题,旨在提高干扰机的能量效率,通过建立最优信道选择及相应能量分配的混合整数规划模型,给出了获得最优干扰策略的必要条件;基于此必要条件,提出了获得最优干扰策略的EEOAS算法,并通过数值仿真实验验证了所提算法的有效性。未来工作面临的挑战为只破解对方部分传输信息时如何制定最优干扰策略。

