Effect of crystallographic orientations on transport properties of methylthiol-terminated permethyloligosilane molecular junction

Ming-Lang Wang(王明郎)， Bo-Han Zhang(张博涵)， Wen-Fei Zhang(张雯斐)，Xin-Yue Tian(田馨月)， Guang-Ping Zhang(张广平)， and Chuan-Kui Wang(王传奎)

School of Physics and Electronics，Shandong Normal University，Jinan 250358，China

Keywords: molecular electronics，crystallographic orientations，non-equilibrium Green’s function

1. Introduction

Single-molecule electronics aiming to drive electronic component miniaturization have achieved considerable progress in the recent years.[1，2]Since the first rectifier was proposed by Aviram and Ratner，[3]functional single-molecule junctions have been fabricated by investigating the electron transport properties for various applications， such as molecular rectifiers，[4–6]molecular conducting wires，[7–9]molecular switches，[10–12]and molecular transistors.[13–15]In this context， understanding and controlling the electron transfer process based on the core functional molecules between electrodes is essential for developing the single-molecule junctions. The single-molecule junction conductance has been theoretically and experimentally verified to primarily depend on the molecular geometry and molecule–electrode interface，which includes factors like anchoring groups， interfacial geometry， and electrode characteristics.[16–23]Therefore， suitable anchoring groups and electrode materials must be determined for designing high-performance single-molecule devices. Common anchoring groups for attaching metal electrodes include pyridine， amino groups， carboxylic acids， nitriles， and isonitriles， among which thiol is more popular as a linker because it forms stable mechanical and electronic contacts.[24–29]After systematically comparing the conductance values of alkane molecular chains with various anchoring groups，Chenet al.demonstrated that Au–thiol contributes the lowest contact resistance，whereas the conductance decay constant is virtually independent of the anchoring groups.[30]In addition， the metal electrodes in molecular junctions can change the Fermi level and influence the energy alignment with the molecular conducting energy level. In this context，several studies have reported that the conductance is strongly dependent on the electrode materials used for constructing single-molecular devices.[31–33]Owing to their lower work function， the molecular junctions formed with Ag electrodes are less conductive than those formed with Au electrodes for amine-terminated oligophenyl and alkane molecules.[34]Furthermore， the varying of electrode crystallographic orientations can result in the large variations in electronic transport properties of molecular junctions.[35–45]Moreover， the high and low conductance measured in alkanethiol molecular junctions are attributed to the electrode orientation，which can tune the molecule–electrode interaction.[35]For aromatic thiophene-based molecules， the (110) crystallographic orientation exhibits superior constructive conductance and negative differential conductance(NDR).[40]In particular，the NDR behavior is verified based on switching molecular junctions for utilizing the electrode orientations.[37]

As the most prevalent material in integrated circuits，bulk Si can be considered as a series of cross-linked Si monatomic chains in one-dimensional structures. Since the first report on permethyloligosilanes short chains exhibiting electronic properties different from those alkane analogs， the saturatedσconjugated permethyloligosilanes have been reported to show a variety of rich electronic properties.[46–56]After the geometry of the terminal methylthiomethyl group was connected to Au electrodes， the permethyloligosilanes demonstrated the first single-molecular switch operation via a stereoelectronic effect.[53]Moreover， the single-molecule junction conductance trend for thiol-terminated permethyloligosilanes was inversely related to metal work function.[56]To the best of our knowledge， the crystallographic orientation effect of the permethyloligosilane molecular junctions has not yet been investigated. Therefore，it is essential to bridge the knowledge gap concerning this molecule–electrode interface effect.

In this study， the atomic structures and electronic transport properties of methylthiol-terminated permethyloligosilane molecular junctions containing permethyloligosilanes with 6， 7， and 8 Si atoms are investigated based on density functional theory through using the nonequilibrium Green’s function method. Considering the possible nanostructures formed using the scanning tunneling microscope breakjunction technology，[35，52]a face-centered crystal Au/Ag with the crystallographic orientations of (111) and (100) is used as the electrodes. The calculations reveal that the low-bias conductance calculated in the linear response limit is dominated by electronic tunneling between the terminal metal–S bonds formed at the metal–molecule interfaces for all molecular junctions considered in this work. The low-bias conductance exponentially decreases with the number of Si atoms in the permethyloligosilane backbone increasing from 6 to 8.More importantly， the results of this study suggest that the interfacial coupling is determined by the electrode characteristics. In the case of the (111) crystallographic orientation，the interfacial coupling between the interfacial Au–S states is stronger than that between the interfacial Ag–S states， resulting in a large low-bias junction conductance. In contrast， the interfacial coupling between interfacial Au–S states is weaker than that between interfacial Ag–S states for the(100)crystallographic orientations，which yields a small low-bias junction conductance.

2. Calculation method

We employed the Atomistix ToolKit (ATK) software package to optimize the geometric structures and evaluate the electronic structures of molecules and molecular junctions.[57，58]The ATK is a highly efficientab initiocode for implementing numerical simulations of large systems，wherein the norm-conserving Troullier–Martins pseudopotentials are used to describe the core electrons， and the finiterange numerical orbital basis set is used for describing the valence electrons.[59–61]In particular， the C， H， S， Si， Au， and Ag atoms comprising the molecules and molecular junctions considered herein are described using a double-zeta plus polarization (DZP) basis set. The generalized gradient approximation (GGA) formulated by Perdew–Burke–Ernzerhof relates to the exchange–correlation functional.[62]Additionally，the real-space grid integration was considered by an equivalent cutoff of 300.0 Ry (1 Ry=13.6056923(12) eV)， and a 4×4k-point sampling was employed in the transverse direction， with a periodic boundary condition used. The geometry optimization was accomplished using the standard conjugate gradient method until the energy tolerance was lower than 1.0×10-4Hartree(1 Hartree=4.3597×10-18J)and all atomic forces were lower than 0.02 eV/˚A.

Subsequently，the transport properties of molecular junctions were evaluated using ATK，which effectively implements the nonequilibrium Green’s function calculations.[63]Moreover， the molecular junctions include a single molecule and 12 atomic layers of the metal electrodes. The periodic boundary conditions were applied to the direction perpendicular to the transport direction.The charge density was integrated over 30 energy points along the semicircle， eight points along the line in the complex plane， and eight poles in the Fermi function with an electronic temperature of 300 K.The transmission spectrumT(E)of the molecular junctions was obtained from the following equation:

whereG0=2e2/hdenotes the conductance quantum.erepresents the electron charge，hrefers to the Planck’s constant，andEFis the Fermi energy.

3. Results and discussion

First， the atomic structure and the electronic structure of the isolated permethyloligosilane are investigated in a transextended conformation. The methylthiol-terminated oligosilanes with 6，7，and 8 Si atoms(denoted as Si6，Si7，and Si8，respectively)are used as the central conductive molecules.For all isolated molecules， the Si atoms in the oligosilane backbone are coplanar with the terminal S atom and C atom in methylene. The interatomic bond length is independent of the number of Si atoms， and the length of C–S， C–Si， and Si–Si bonds are 1.82，1.91，and 2.37 ˚A，respectively，corresponding to the electronic structures presented in Fig. 1. The highest occupied molecular orbital(HOMO)orbital and HOMO-1 orbital， shown in the inset in Fig. 1， are degenerate， and both orbitals are contributed by terminal S 3p localized atomic orbitals perpendicular to the molecular plane. In contrast to the localized characteristics， both lowest unoccupied molecular orbital(LUMO)and HOMO-2 are delocalized across the entire molecular backbone. Although theσ-bond comprising the Si backbone is similar to that in alkane，the oligosilanes exhibit the specialσconjugation due to the reduced energy gap，with the number of Si atoms increased，as depicted in Fig.1.

The optimized geometric structure of the Ag(111)–Si6–Ag(111)molecular junction is illustrated in Fig.2(a)，wherein two methylthiol groups connect to the Ag adatoms on electrode surfaces cut from a face-centered crystal Ag bulk along the(111)direction. The optimized Ag–S covalent bond length is 2.35 ˚A，whereas the C–Si bond length and Si–Si bond length are the same as those of isolated molecule，indicating that the molecular geometry is stable both before and after forming the molecular junction. The equilibrium transmission spectrum is obtained as depicted in Fig.2(b). Two prominent transmission peaks at-1.02 eV and 3.25 eV decay rapidly towardsEF. In particular，a small shoulder peak centered at-0.33 eV occurs.The transmission coefficient atEFis 8.9×10-3. To further understand these peaks，the projected density of states(PDOS)on the terminal S and Ag atoms and the eigenchannel are evaluated and shown in Figs. 2(c)–2(e). The narrow peak aboveEFis caused by the weak coupling between the Ag p-orbitals and S 3p-orbitals，which are obtained from the LUMO orbitals by comparing the eigenchannel calculated at 3.25 eV with the frontier molecular orbitals (FMOs) as indicated in the insets of Fig. 1. Although the PDOS at-0.33 eV is exceedingly high，the corresponding transmission peak is extremely small，which is caused by S 3p-orbitals perpendicular to the molecular plane，resulting in weak coupling with backboneσ-bond(Fig. 2(e)). Moreover， the broadened peak underEFextends from-0.86 eV to-1.02 eV， which is primarily contributed by Ag 4d and S 3p orbitals. Furthermore，the broadened transmission peak in Fig. 2(e) is dominated by the HOMO and HOMO-1， wherein the splitting of energy level is caused by interaction between two interfacial states after having been connected to electrodes.The eigenchannel calculated atEFexhibits the fundamental density distribution on the left-terminal S atoms and Ag atoms as depicted in Fig.2(e)，indicating that the interfacial hybrid states provide a dominant contribution to electron transfer in the vicinity ofEF. As the isovalue of eigenchannel isosurface decreases from 0.15 ˚A-1.5(eV)-0.5to 0.05 ˚A-1.5(eV)-0.5， the eigenchannel exhibits an extension along the molecular backbone through the S–Cσchannel and Si–Siσchannel. The results further demonstrate that the states contributing to the small shoulder does not contribute to the transmission atEF，regardless of their vicinity toEF.

Similar junctions are constructed using Si7 (Si8)molecule and denoted by Ag(111)–Si7(Si8)–Ag(111)， and the optimized geometric structures are almost unchanged.The Ag–S， S–C， and C–Si bond length are calculated to be 2.37 ˚A (2.36 ˚A)， 1.83 ˚A (1.83 ˚A)， and 1.92 ˚A (1.91 ˚A) for Si7(Si8)molecular junctions，respectively. Overall，the trend of the equilibrium transmission curve is similar to that of the Ag(111)–Si6–Ag(111)junction，except that the energy gap between the HOMO and LUMO decreases，and the HOMO shifts towardEFas the molecular backbone elongates. Counter intuitively，the calculated transmission coefficient atEFdecreases from 8.9×10-3and 4.97×10-3to 3.4×10-3as the molecule changes from Si6 into Si8，which is prominently expressed in the inset with the transmission coefficients using logarithmic coordinates(Fig.2). This is ascribable to the longer molecular backbone and weaker interfacial coupling. Therefore， the conductive mechanism of the Ag(111)–Si6(Si7，Si8)–Ag(111)molecular junction is primarily dominated by the electronic tunneling between the two localized Ag–S interfacial states that can be tuned by the oligosilane chain. For the three molecular junctions， the conductance calculated in the linear response limit decreases exponentially with the number of Si atoms， which can be expressed asG～exp(-βn)， whereGdenotes the junction conductance，nthe number of Si atoms，andβthe conductance decay constant. Theβvalue is fitted as 0.52 per Si atom，which corresponds well with the experimentally measured value of 0.60±0.03 per Si atom. Furthermore，the tunneling mechanism is confirmed based on the discussed length-dependent junction conductance.

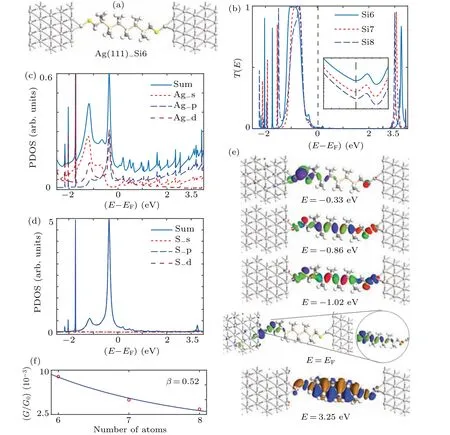
Fig. 2. Optimized atomic structure and electronic transport properties of Ag(111)–Si6–Ag(111) molecular junction with Ag electrode along (111)directions: (a) optimized atomic structure; (b) equilibrium transmission spectra calculated for Ag(111)–Si6(7，8)–Ag(111) molecular junctions， with inset showing transmission coefficients in logarithmic coordinates; (c) PDOS projected onto adatom Ag atom; (d) PDOS projected onto terminal S atom; (e)eigenchannel calculated at EF， -0.33， -0.86， -1.02， and 3.25 eV.The isovalue is 0.15 ˚A-1.5 (eV)-0.5， whereas it decreases to 0.05 ˚A-1.5(eV)-0.5，as shown in the inset of eigenchannel calculated at EF;(f)conductance decay constant.

Thereafter，the Au(111)–Si6–Au(111)molecular junction is constructed， the optimized geometric structure of which is shown in Fig. 3(a). In this structure， two methylthiol groups connect the Au adatoms on the electrode surfaces cut from the face-centered crystal Au bulk along the (111) direction. The optimized bond length of the Au–S covalent bond is 2.30 ˚A，and the interatomic separation of the central molecular backbone is almost identical to that in the Ag(111)–Si6–Ag(111)molecular junction. This indicates that the molecular geometry is independent of the electrode characteristics， and the Au–S bond is slightly stronger than the Ag–S bond， which may enhance the low-bias conductance. The transmission coefficient atEFis calculated to be 1.70×10-2，which is indeed higher than that of the Ag electrode. This enhanced conductance can be ascribed to the Au 5d and S 3p orbitals(Figs.3(c)and 3(d))，which are dominated by the HOMO and HOMO-1 of Si6 molecule (Fig. 3(f); inset in Fig. 1). Notably， the Au 5d and S 3p orbitals centered at-0.39 eV do not contribute to the transmission due to orbital symmetry mismatch，which also appeared in the alkane–thiol molecular junctions.[65]The eigenchannel extending along the molecular backbone through the S–C，and Si–Siσchannel is similar to that in the Ag(111)–Si6–Ag(111)， which indicates that the transmission atEFis caused by the tail effect of these peaks underEF. Similarly，with the longer molecules connected to the Au electrodes，the conjugate characteristic is enhanced as the transmission coefficient atEFdecreases as depicted in the inset of Fig. 3(b).In particular，the transmission coefficients atEFare evaluated to be 8.8×10-3for Au(111)–Si7–Au(111) and 6.03×10-3for Au(111)–Si8–Au(111). According to the same analysis method， the reduced transmission coefficient primarily originates from reduced interfacial coupling between two Au–S states at both interfaces，wherein the tunneling mechanism can be further confirmed by reducing the widths of the transmission peaks contributed by the HOMO and HOMO-1 during backbone elongation. Further， the conductance decay constant per atom is evaluated to be 0.57，which is consistent with the experimental value of 0.64±0.02 per Si atom. In addition，the separation between the peaks acrossEFfor Au(111)–Si6(Si7，Si8)–Au(111) is 4.02 (3.80 and 3.64) eV， which accords well with that for the Ag(111)–Si6(Si7，Si8)–Ag(111)molecular junction. Thus， these results demonstrate that the transport properties are influenced by the electrode characteristics.

Fig. 3. Optimized atomic structure and electronic transport properties of Au(111)–Si6–Au(111) molecular junction with Au electrode along (111)direction. (a) Optimized atomic structure; (b) equilibrium transmission spectra calculated for Au(111)–Si6(7，8)–Au(111) molecular junctions， with inset indicating transmission coefficients in logarithmic coordinates; (c) PDOS projected onto adatom Au atom; (d) PDOS projected onto terminal S atom;(e)conductance decay constant;(f)eigenchannel calculated at EF and-0.81 eV.

Fig. 4. Conductance calculated in linear response limit as a function of Si atom number in electrode(111)direction.

However， Liet al.recently reported that the electrical contact provided by Ag electrodes for thiol-terminal silanes is superior to that provided by Au electrodes. In addition，the higher conductance in the Ag electrode than that in the Au electrode is in discrepancy with previously calculated result.[56]Moreover， Sen and Kaun reported that Au(100)electrodes can offer a higher conductance than Au(111)electrodes in alkanedithiol single-molecule junctions.[35]Therefore， molecular junctions constructed by symmetrically connecting molecules to the pyramid tip atom on the surfaces from the face-centered crystal metal bulk along the (100) direction are investigated. The Ag(100)–Si6–Ag(100) molecular junction is presented in Fig. 5(a). The Ag–S bond length is optimized to be 2.36 ˚A. Moreover， the interatomic separations of S–C， C–Si， and Si–Si are calculated to be 1.83，1.91，and 2.37 ˚A，respectively，maintaining them with those of the isolated molecules. Furthermore，the equilibrium transport spectrum is similar to that of Ag(111)–Si6–Ag(111)with two prominent transmission peaks acrossEF. The small variations are that the peak underEFshifted slightly downward and the plateau becomes narrower than that of Ag(111)–Si6–Ag(111).In the PDOS depicted in Figs. 5(c) and 5(d)， the peaks underEFare attributed to the Ag 4d–5s and S 3p orbitals，which are dominated by the HOMO and HOMO-1 based on the inspection of FMOs of Si6 molecule (inset of Fig. 1). Additionally，the eigenchannel in Fig.5(f)indicates that the transmission atEFis dominated by electronic extension originating from the interfacial Ag–S state， and the HOMO and HOMO-1 constitute the conductive channel. As the molecular backbone elongates， the reduced interfacial coupling narrows the plateau of the peak underEFand reduces the transmission atEF. The equilibrium transmission coefficients atEFfor Ag(100)–Si7–Ag(100) and Ag(100)–Si8–Ag(100) are calculated to be 2.23×10-3and 1.42×10-3， respectively. The fitting decay constantβis evaluated to be 0.52 per Si atom(Fig. 5(e))， which accords with the counterpart for Ag(111)–Si6(7，8)–Ag(111). These findings further corroborate that the electron tunneling passes through the same molecular orbitals.

Fig. 5. Optimized atomic structure and electronic transport properties of Ag(100)–Si6–Ag(100) molecular junction with Au electrode along (100)direction. (a)Optimized atomic structure;(b)equilibrium transmission spectra calculated for Ag(100)–Si6(7，8)–Ag(100)molecular junction，with inset showing transmission coefficient in logarithmic coordinate; (c)PDOS projected onto adatom Ag atom; (d)PDOS projected onto terminal S atom; (e)conductance decay constant;(f)eigenchannel calculated at EF and-1.0 eV.

Finally， we come to investigate the Au(100)–Si6–Au(100) molecular junction. The optimized geometric structure is illustrated in Fig.6(a). The optimized bond lengths of Au–S，S–C，C–Si，and Si–Si are 2.30，1.82，1.92，and 2.36 ˚A，respectively，which are independent of crystallographic orientation. The prominent transmission peak underEFin Fig.6(b)is dominated by the interaction between the Au 5d and S 3p orbitals as shown in Figs. 6(c) and 6(d). Furthermore， the eigenchannel in Fig.6(f)indicates that the peak is dominated by the HOMO and HOMO-1 of the isolated Si6 molecule，and that the transmission atEForiginates from its tail effect. As the central molecule varies from Si6 to Si7 to Si8， the interfacial coupling weakens according to the narrower plateau of the peak underEF， which consequently reduces the transmission coefficient from 2.93×10-3through 1.86×10-3to 1.13×10-3， regardless of the peak progressing upward to theEF. The tunneling mechanism between the interfacial Au–S states can be corroborated by the exponential decay function defined based on the decay constantβ= 0.45 in Fig. 6(e). Moreover， the conductance in the linear response limit is derived as a function of the number of Si atoms， and the results are shown in Fig. 7. In stark contrast to the results of the electrode (111) crystallographic orientations， the low-bias conductance of the Ag(100) electrode is higher than that of Au(100)， which corresponds to experimental measurement.[56]The average coupling coefficients for the Au(100)–Si6–Au(100)， Au(100)–Si7–Au(100)，and Au(100)–Si8–Au(100)molecular junctions are calculated to be 50.9， 38.0， and 24.5 meV，respectively. This is because the reduced coupling between the interfacial Au–S states can lead the low-bias conductance to decrease. For Ag(100)–Si6–Ag(100)， Ag(100)–Si7–Ag(100)， and Ag(100)–Si8–Ag(100)molecular junctions， the calculated coupling coefficients are 62.4， 39.7， and 28.3 meV， which can explain the conductance varying with the molecular length. More importantly，the Ag(100) electrode offers superior electronic contact with methylthiol-terminated permethyloligosilanes in comparison with the Au(100) electrode， consequently resulting in higher low-bias conductance.

Fig. 6. Optimized atomic structure and electronic transport properties of Au(100)–Si6–Au(100) molecular junction with Au electrode along(100) directions. (a) Optimized atomic structure; (b) equilibrium transmission spectra calculated for Au(100)–Si6(7，8)–Au(100) molecular junctions， with inset showing transmission coefficient in logarithmic coordinates; (c)PDOS projected onto adatom Au atom; (d)PDOS projected onto terminal S atom;(e)conductance decay constant;(f)eigenchannel calculated at EF and-0.94 eV.

Fig.7. Conductance calculated within linear response limit as a function of Si atom number for electrode with crystallographic orientation of(100).

4. Conclusions

The density functional theory， combined with the nonequilibrium Green’s function， is used to investigate the atomic structures and electronic transport properties of molecular junctions，wherein permethyloligosilanes with 6，7，and 8 Si atoms are symmetrically connected to a face-centered crystal Au/Ag electrode along the(111)direction and the(100)direction. The derived calculations reveal that the low-bias conductance is dominated by electronic tunneling between metal–S bonding states at both molecule–electrode interfaces. Although theσconjugation increases， the decreasing of coupling， which is due to tuning the central permethyloligosilane backbone length， leads the low-bias conductance to decay exponentially. In addition， the interfacial coupling can be mediated by the electrode crystallographic orientations.For electrodes along the (111) direction， the conductance of molecules connected to the Au electrodes is higher than that of the molecules connected to the Ag electrodes. In contrast，for electrodes along the(100)direction，the conductance of the molecular junctions connected to the Ag electrode is higher than that of the molecules connected to the Au electrode. The findings of this study are conducive to understanding the transport mechanism and mediating the interactions between the two metal–molecule interfaces by suitable electrode crystallographic orientations，thereby improving the electronic properties of permethyloligosilanes molecular junctions.

Acknowledgements

Project supported by the Shandong Provincial Natural Science Foundation， China (Grant No. ZR2019PA022) and the National Natural Science Foundation of China (Grant No.21933002).