Practical security analysis of continuous-variable quantum key distribution with an unbalanced heterodyne detector

Lingzhi Kong(孔令志)， Weiqi Liu(刘维琪)， Fan Jing(荆凡)， and Chen He(贺晨)

College of Information Science and Technology，Northwest University，Xi’an 710127，China

Keywords: continuous-variable，quantum key distribution，heterodyne detector

1. Introduction

Quantum key distribution(QKD)enables two distant authorized parties (Alice and Bob) to exchange a secret key basesd on the laws of Heisenberg’s uncertainty principle and no-clone theory， which can be divided into the discrete variable quantum key distribution (DVQKD) and CVQKD.[1–6]Focusing on the most favorable CVQKD protocol， the Gaussian-modulated coherent state (GMCS) protocol，[7–13]which encodes the key information on the quadratures(XandP)of coherent states，the modulated states will be sent to Bob along with the LO. Then Bob randomly measures one of the two quadratures using a homodyne detector， or both quadratures simultaneously with a heterodyne detector. So far， the GMCS scheme has been experimentally carried out in both laboratory[14–16]and field tests.[17，18]Furthermore， the composable security of this scheme against collective attack has been established.[19，20]

However， the imperfections of devices and applications used in the practical system may threaten the security of the system. The imperfections include the laser source，[21–23]the local oscillator，[24，25]the beam splitter (BS)，[26–28]the basis choice，[29，30]and the detector.[31–37]In the implementation of GMCS protocols， Bob may not need to randomly switch his measurement basis using the heterodyne detector. Theoretically， the scheme gives a higher key rate and allows simpler and higher bandwidth quantum cryptographic experiments.However， the BS used in the heterodyne detector may be imperfect and the four photodiodes may be mismatched. Such imperfections will lead to an imbalance of the heterodyne detector， and further influence the parameter estimation and the lower bound of the secret key rate of CVQKD system and，finally，may bring security loopholes for Eve to attack the system.

In this paper， we investigate the practical security of a GMCS CVQKD system with an unbalanced heterodyne detector. We find that the imbalance will bring in extra excess noise to the system and the lower bound of the secret key rate will be decreased due to the imperfect BS and the mismatch of four photodiodes. Moreover， the secret key rate decreases more severely with the increase in the degree of imbalance and the extra excess noise is proportional to the intensity of the LO under the same degree of imbalance. To resist this imperfection，a countermeasure is proposed.

This paper consists of six sections. In Section 2， we describe the perfect heterodyne detector in detail. Then the practical unbalanced heterodyne detector in CVQKD is investigated in Section 3 and the secret key rate against collective attack in the above case is investigated by theoretical calculation and simulation in Section 4. In Section 5， a possible countermeasure is proposed to resist the imperfection induced by the unbalanced heterodyne detector. In Section 6，we give the conclusion.

2. The balanced heterodyne detector

The balanced heterodyne detector mainly consists of four beam splitters with ideal beam splitting ratio， two pairs of matched photodiodes with the same quantum efficiency， two subtractors and two amplifiers with transimpedanceg. The structure of heterodyne detector is shown in Fig.1. The quantum and LO signal are divided into two beams via two 50:50 beam splitters. Then，the quadraturesXandPof the quantum signal are measured simultaneously by two homodyne detectors on the upper and lower arms.It is worth noting that the LO on the lower arm is phase-shifted by 90°to measure quadratureP.

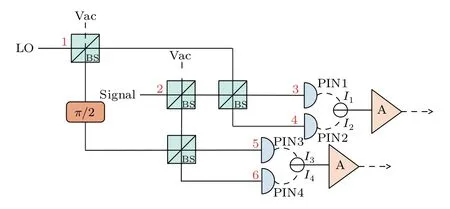
Fig.1.The structure of the heterodyne detector.BS:beam splitter;PIN1，2，3，4:photodiode with quantum efficiency η1，2，3，4;A:transimpedance amplifer.

In heterodyne detection，Bob generally converts the photons into photocurrent. Here we introduce quantum efficiencyηto characterize the ability of converting incident light into photocurrent，which is the ratio of the average number of photoelectrons generated per unit time at a certain wavelength to the number of incident light photons. It is supposed that the average electron number of photocurrent output by the photodiode isNe， and the average photon number of the incident light on the photodiode isNi. Therefore， the average optical powerPacan be defined as:

wherehis the Planck constant，νis the optical wavelength andτis the duration of light incident on the photodiode. For convenience of analysis，we can defineτ=1 and the average photon number of the incident light can be expressed as

According to the definition of quantum efficiency，ηcan be written as

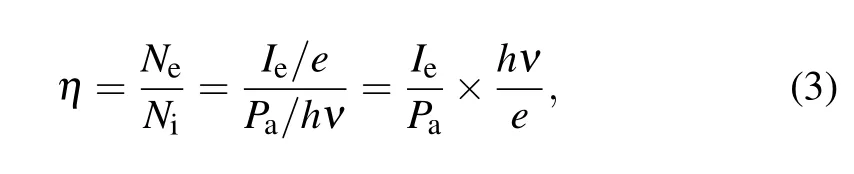
whereIeis the average output photocurrent of the photodiode andeis a constant denoting the amount of negative charge carried by a single electron. It is noteworthy thatIe/Padescribing the responsivity of photodiode can be labeled asRpin. Consequently，equation(3)can be modified as

When implementing heterodyne detection， the vacuum state is introduced via the 50:50 BS as shown in Fig.1. Therefore，the final measured quardraturesXandPwill be coupled into a vacuum fluctuation. The corresponding output of the four photodiodes can be expressed as follows:

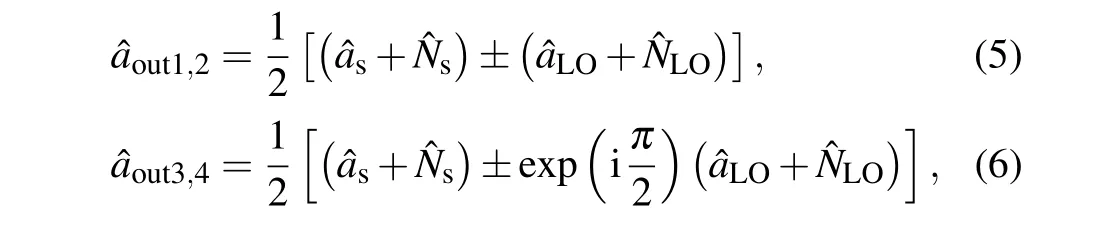
where ˆasdenotes the mode of quantum signal optical field，ˆaLOdenotes the mode of the LO signal optical field， ˆNsand ˆNLOdepict the vacuum noise introduced into the quantum signal and LO signal respectively due to the implementation of the heterodyne detection.Then the photon number of the four output modes can be shown as follows:

According to the definition of quantum efficiency， the photocurrent output of these four photodiodes can be calculated as follows:

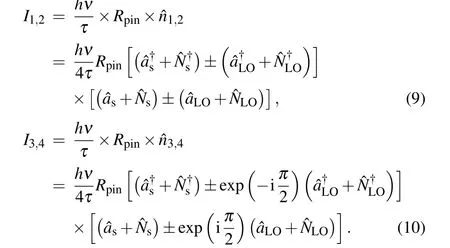
Then， the differential current output on the upper and lower arms can be given by

3. The practical unbalanced heterodyne detector

As aforementioned，the practical heterodyne detector may be unbalanced and imperfect due to the limitations of the BS and the photodiode. For example，the splitting ratio of the BS may not be ideal and the four photodiodes maybe mismatched.So as to distinguish the characteristics between a balanced heterodyne detector and unbalanced heterodyne detector， we introduce an additional parameterLi j(i=1，2;j=3，4，5，6)to demonstrate the effect of the loss from input portito output portj，as shown in Fig.1. And considering the mismatch of these four photodiodes，the quantum efficiency of the photodiodes can be defined asη1，η2，η3， andη4， respectively.Considering the imperfections of the heterodyne detector，the corresponding output of the four photodiodes can be modified as

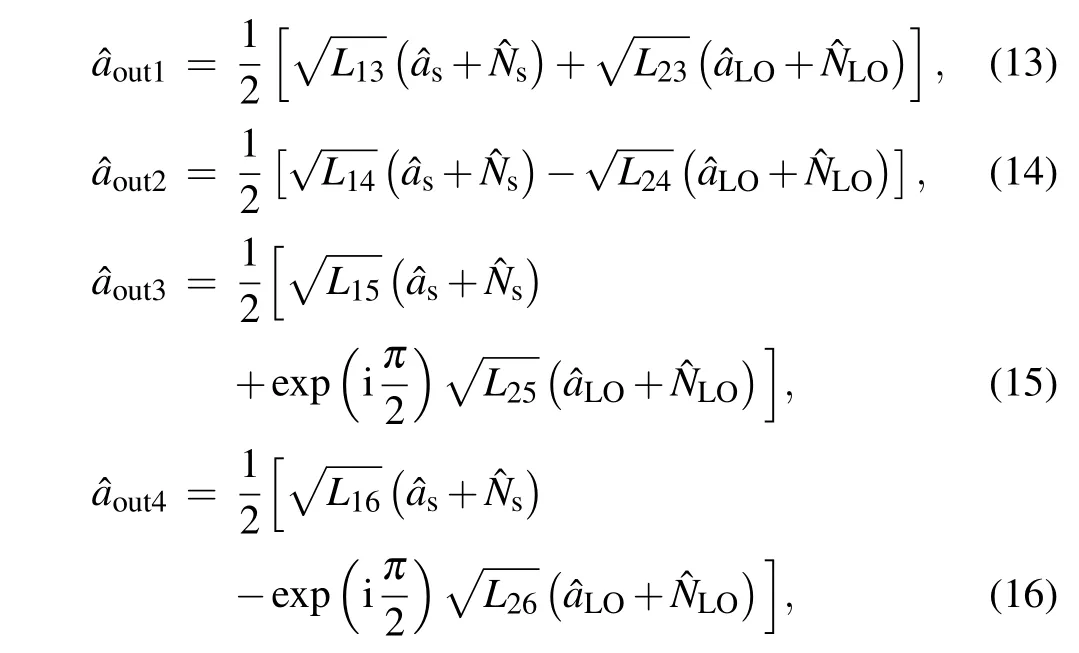
and the photon number of the four output photodiodes can be rewritten as follows:

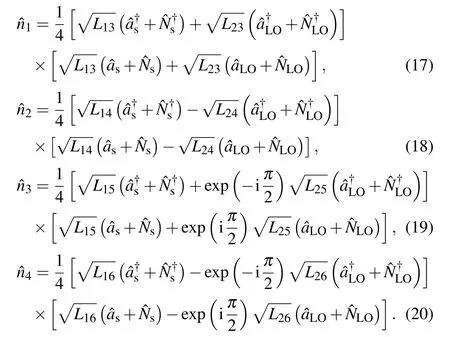
Referring to Eq.(4)，the practical responsivity of the four photodiodes of the unbalanced heterodyne detector can be expressed as follows:

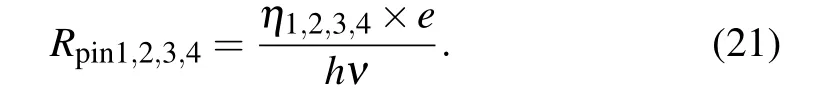
Consequently，the photocurrent output of the four photodiodes can be calculated as follows:

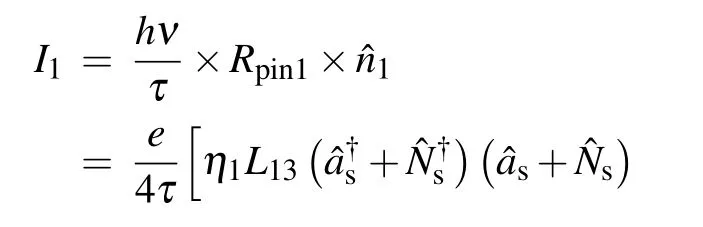
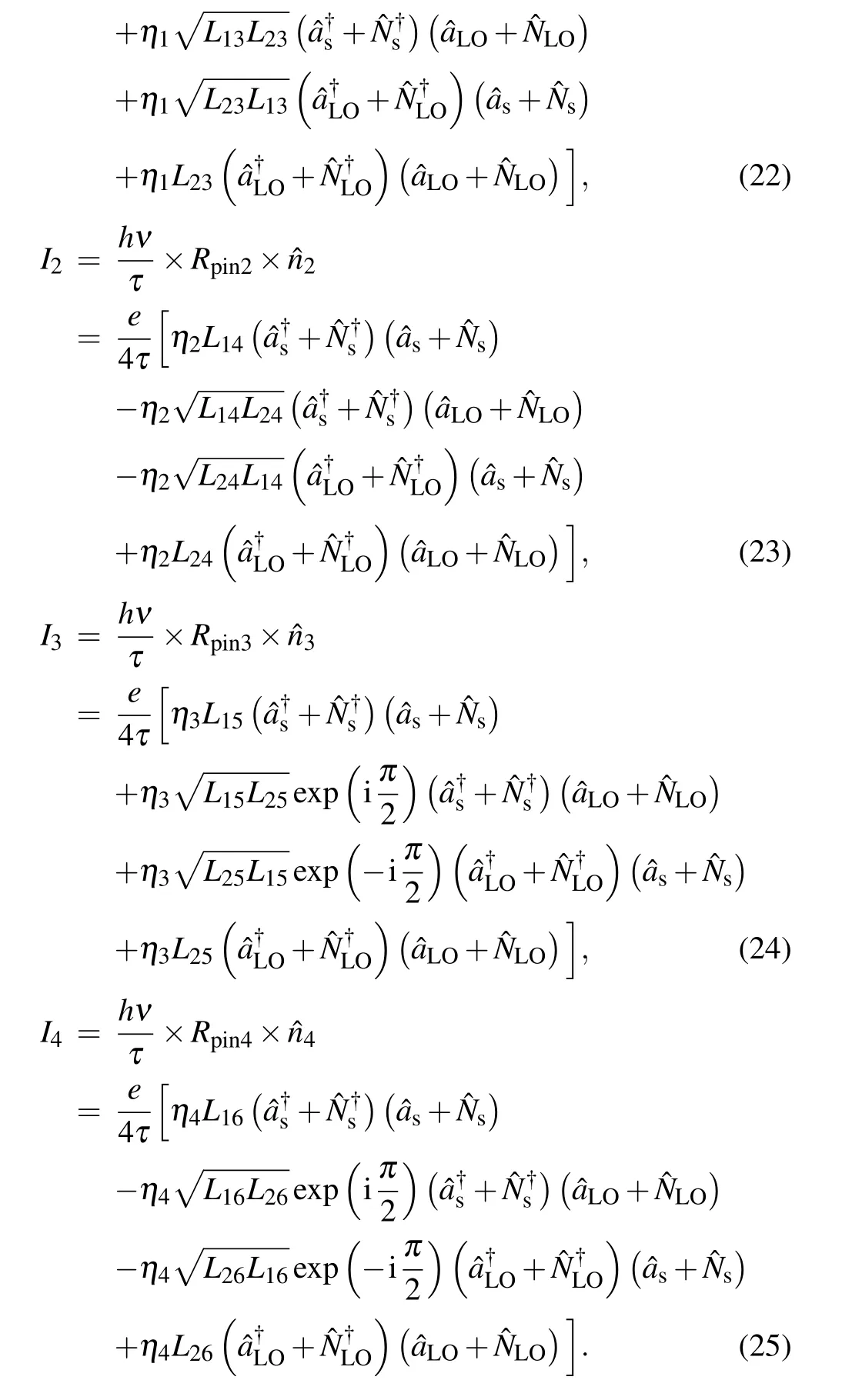
Then，the practical differential current output on the upper and lower arms can be expressed as

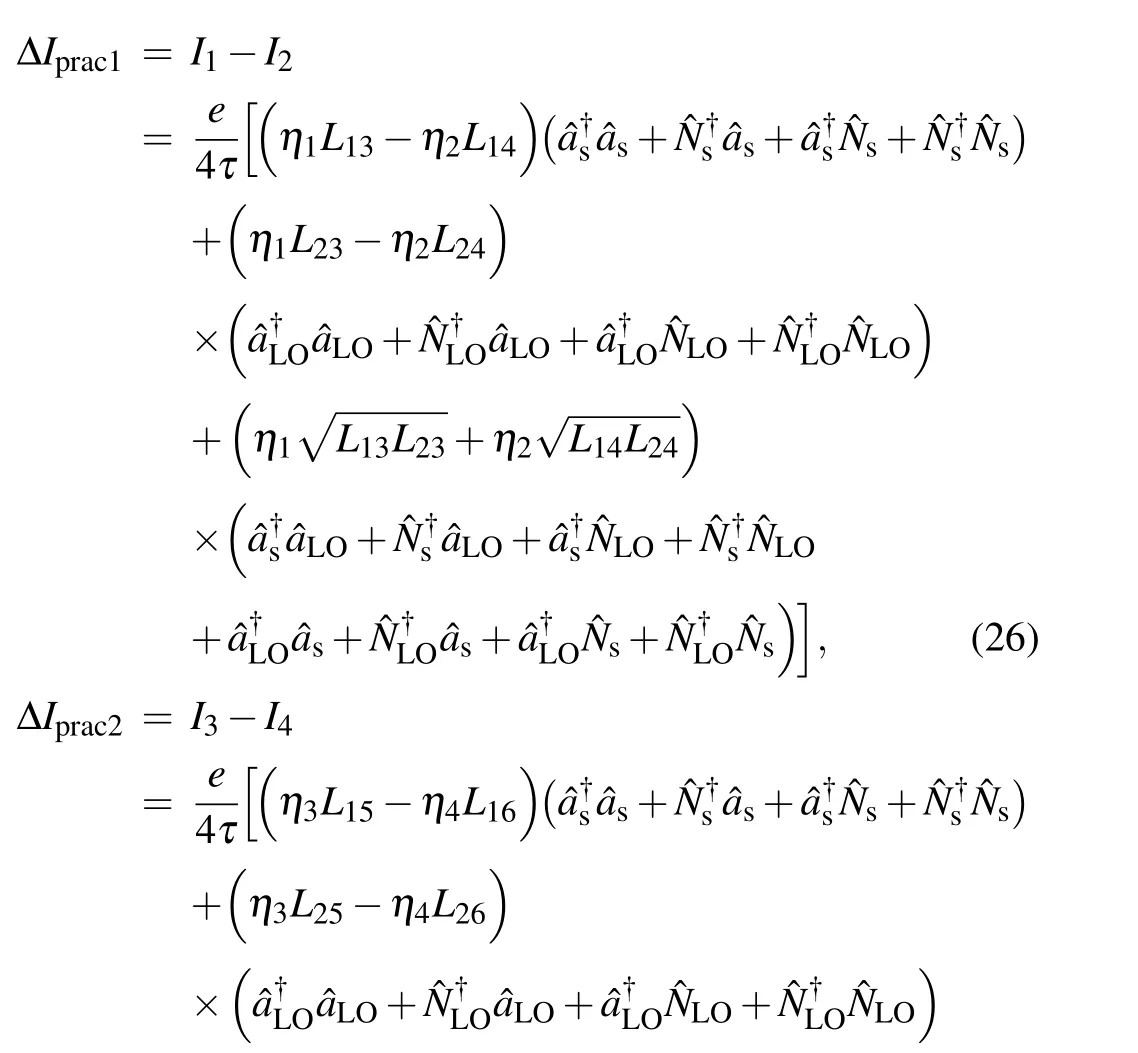
Correspondingly， the output voltage of the upper and lower arms of the practical heterodyne can be expressed as follows，

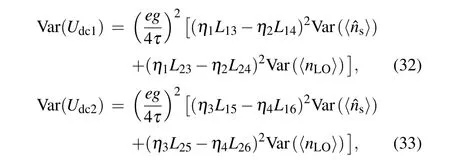
then the variance ofUdc1andUdc2can be obtained as follows:where Var(〈ˆns〉) = (V2A/4)RINsB and Var(〈nLO〉) =(τ/hν)2〈PLO〉2RINLOB， where RIBsand RINLOrepresent the corresponding relative intensity noise of the quantum signal and the local oscillator，〈Ps〉and〈PLO〉depict the average intensity of quantum signal and local oscillator. Then the excess noise induced by the direct components will be given by

4. Performance analysis of the CVQKD system with an unbalanced heterodyne detector

As mentioned before，the splitting ratio of the BS may not be ideal and the four photodiodes maybe mismatched， which will cause an imbalance in heterodyne detector. As a result，extra excess noise is induced by these imperfections. For the convenience of analysis， the imperfections of the BS can be viewed as a part of the mismatch of the four photodiodes. To demonstrate the influence of an unbalanced heterodyne detector on the CVQKD system， here we consider the following four cases: (i)η1=η2=η3=η4; (ii)η1=η2=η3／=η4;(iii)η1=η2／=η3／=η4;(iv)η1／=η2／=η3／=η4.

According to Eqs.(1)，(34)and(35)，we firstly investigate the relationship between the excess noise and the intensity of the local oscillator under the four cases mentioned above， as shown in Fig. 2. The number of photons of the local oscillator light ranges from 108to 109. From top to bottom，the four lines indicate the relationship between the excess noise and the intensity of the LO when the four photodiodes are completely mismatched to fully matched. From Fig. 2， we find that the excess noise is proportional to the intensity of LO under the same degree of mismatched quantum efficiency and the extra excess noise will increase with the increase in the degree of imbalance. In other words，the greater the degree of mismatch of the four photodiodes， the greater the excess noise induced by the unbalanced heterodyne detector.

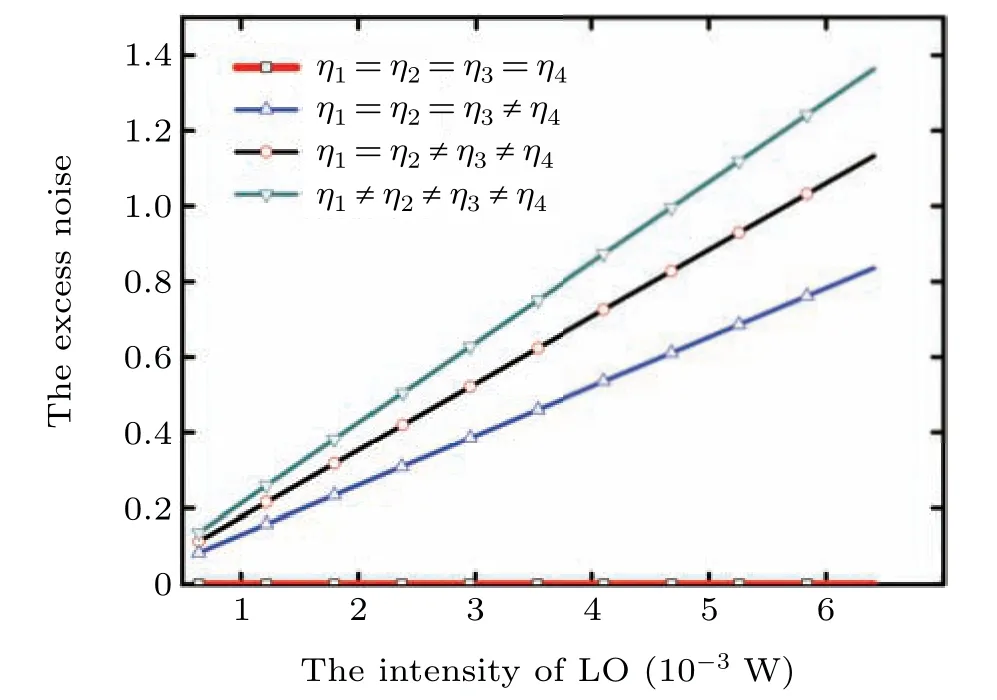
Fig. 2. The relationship between the excess noise and the intensity of the local oscillator under different degrees of imbalance. The simulation parameters are set as follows: elementary charge e=1.602176×10-9， plank constant h=6.62607015×10-34， duration τ =20 ns， optical wavelength ν = 193.4 THz， photon number nLO ∈[108，109]， equivalent bandwidth B=15 MHz，RINs=-210，RINLO=-135，and VA=5.

Then taking the finite-size effect into account，[38]we analyze the secret key rate of the CVQKD system with unbalanced heterodyne detector. The secret key rate of the CVQKD system under collective attack can be given by(see Appendix A for detailed derivation)

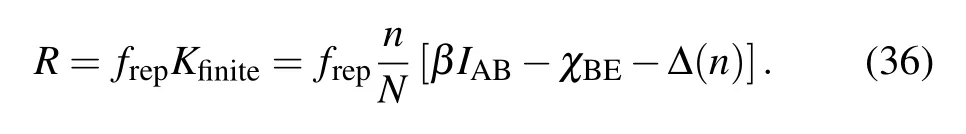
To demonstrate the influence of the imbalance of the heterodyne detector on the secret key rate，we performed a simulation. In the simulation， the repetition frequency of system is fixed to 10 MHz. Curves from top to bottom represent the relationship between the secret key rate and the transmission distance under different degrees of imbalance in Fig. 3.Specifically，the black curve with circle denotes the ideal balanced heterodyne detector withη1=η2=η3=η4， which possesses the maximum transmission distance and secret key rate. The brown curve with squares denotes the most mismatched case withη1／=η2／=η3／=η4that has the minimum transmission distance and secret key rate. From the simulation results， we find that the imperfection of the BS and the mismatch of the four photodiodes will lead to a decrease in both secret key rate and the maximum transmission distance of the practical CVQKD system. Moreover， the security bound and the maximum transmission distance decrease more steeply with increase in the degree of imbalance.

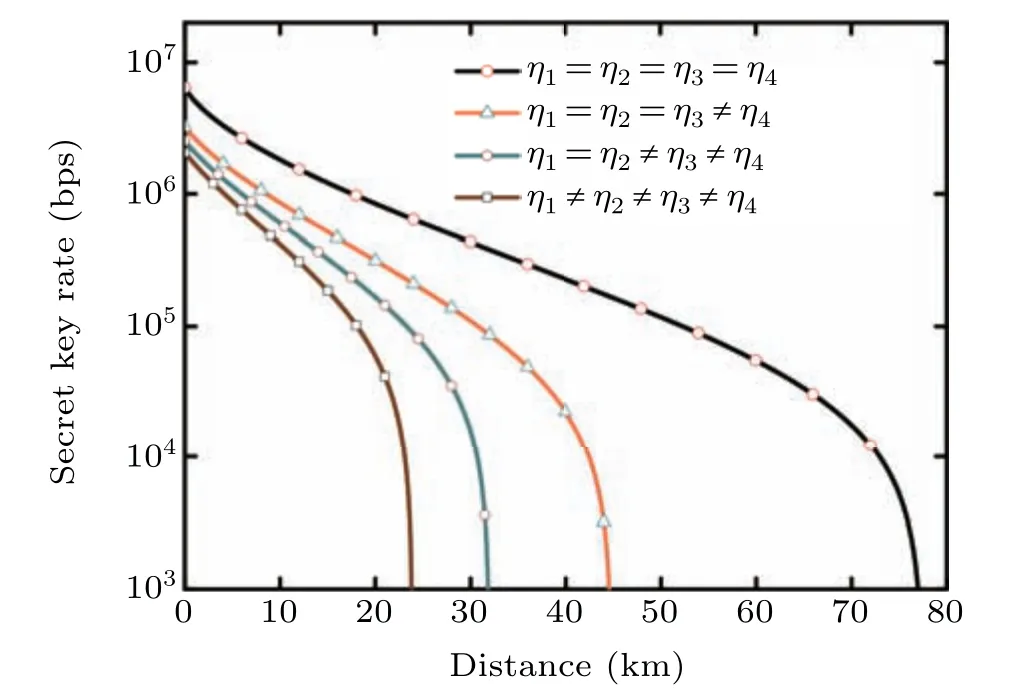
Fig.3. The relationship between the secret key rate and the transmission distance under different degrees of imbalance.The simulation parameters are set as follows: photon number nLO =108， equivalent bandwidth B=15 MHz，excess noise ξ =0.01，electric noise vel=0.01 and reconciliation efficiency β =0.96.

5. A possible countermeasure against the imbalance of the heterodyne detector

In this section，we propose a possible countermeasure to rebalance the CVQKD system with unbalanced heterodyne detector. Commonly， an unbalanced heterodyne detector will induce a mismatch between the intensity of the quantum and LO signal. As an important optical passive device in optical fiber communication， the variable optical attenuator (VOA)can realize the real-time control of the intensity of the signal by attenuating the transmitted optical power.[39]Hence we propose an improved scheme to rebalance the unbalanced heterodyne detector，in which six VOAs are applied in proper situations. As plotted in Fig.4，VOA5，6are set to rebalance arm 5 and arm 6 in red，VOA1，2are set to rebalance arm 1 and arm 2 in green and VOA3，4are set to rebalance arm 3 and arm 4 in yellow.

Based on the previous analysis，a practical heterodyne detector can be regarded as two unbalanced homodyne detector.Therefore， the rebalancing of the heterodyne detector can be derived from that of the homodyne detector. Referring to Ref.[34]，the expected voltage at the output of the homodyne detector〈ˆvH(t)〉is given by，

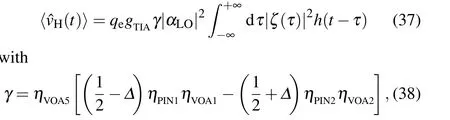
whereh(t) denotes the impulse response. For rebalancing the unbalanced homodyne detector， it is indispensable for us to adjust the attenuation efficiency of the VOAidynamically by monitoring the output voltage mean value〈ˆvH(t)〉in real time.Whent=0，〈ˆvH(t)〉is only equal to zero under the circumstance thatγ=0. And from the Eq.(38)，we can deduce thatγ=0 when(1/2-Δ)ηPIN1ηVOA1=(1/2+Δ)ηPIN2ηVOA2，thus a rebalanced homodyne detector is obtained.So similarly，we can deduce that，

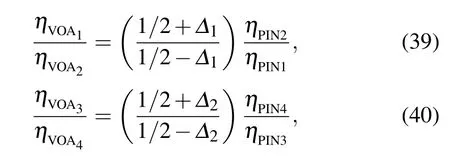
whereηVOAiis the parameter indicating the transmissivity of the VOAiand can be adjusted dynamically. Besides，Δ1andΔ2characterize the imbalance of the upper and the lower homodyne detector respectively， which are the reference values for dynamic adjustment of VOAi. Details are as follows:

(i) WhenΔ1＜0 andΔ2＜0， onlyηVOA1in arm 1 andηVOA3in arm 3 need to be adjusted;

(ii) WhenΔ1＜0 andΔ2＞0， onlyηVOA1in arm 1 andηVOA4in arm 4 need to be adjusted;

(iii) WhenΔ1＞0 andΔ2＜0， onlyηVOA2in arm 2 andηVOA3in arm 3 need to be adjusted;

(iv) WhenΔ1＞0 andΔ2＞0， onlyηVOA2in arm 2 andηVOA4in arm 4 need to be adjusted.

Similarly， the adjustment ofηVOA5，6is the same as that ofηVOA1，2，3，4. Through dynamic adjustment and quantitative analysis of the six VOAs，the extra excess noise caused by the unbalanced heterodyne detector can be eliminated and the performance of the practical CVQKD system can be improved.

Fig.4. The scheme of the countermeasure against the imbalance of the heterodyne detector. VOA: variable optical attenuator. The VOAs are set to rebalance the unbalanced heterodyne detector by attenuating the transmitted optical power of the corresponding arm.

6. Conclusion

Focusing on the practical heterodyne detector with imperfect components， for instance， a BS with non-ideal beam splitting ratio and photodiodes with mismatched quantum efficiency， we investigate the performance of the practical CVQKD system with an unbalanced heterodyne detector. The results show that such imperfections will inevitably induce extra excess noise， which decreases both the maximum secret key rate and the secure communication distance. And as the degree of imbalance increases，the secret key rate and the communication distance decrease more severely. We also find that the extra excess noise caused by the unbalanced heterodyne detector is proportional to the intensity of the local oscillator. Finally， we propose a possible countermeasure using six VOAs to counteract the impact of the unbalanced heterodyne detector to improve the performance of the practical CVQKD system.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 62001383) and the Natural Science Basic Research Plan in Shaanxi Province of China(Grant No.2019JM-591).

Appendix A:Derivation for secret key rate with finite-size effect under collective attack

Considering collective attack， the secret key rate shared between Alice and Bob with finite-size effect can be defined as follows:

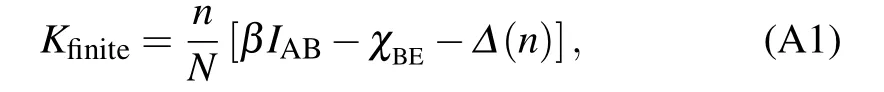
whereNis the length of valid data collected，nis the data length used for the final key rate generation，m=N-nis the data length for parameter estimation，Δ(n) is a function related to privacy enhancement andβis the efficiency of reverse reconciliation. Moreover，IABis the amount of mutual information between Alice and Bob， which can be calculated as follows:

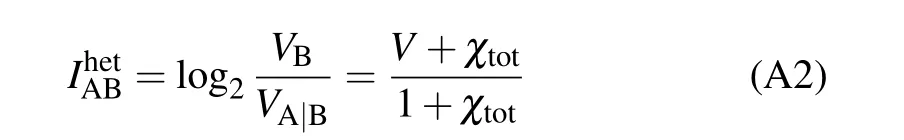
with the parametersV=VA+1，χtot=χline+(χhet/T)，χline=1/T-1+ξ，χhet=(2(1+vel)/η)-1; hereVAis the modulation variance of Alice，χtotrepresents the total noise at the input of the channel，Tis the transmittance of the channel，χhetis the additive noise of the heterodyne detector，χlineis the additive noise of the channel，velis the electric noise of the heterodyne detector andξis the excess noise of the system.

Besides，χBErepresents the maximum amount of information that Eve can obtain from Bob， which is restricted by the Holevo bound.[40]χBEcan be expressed as follows:

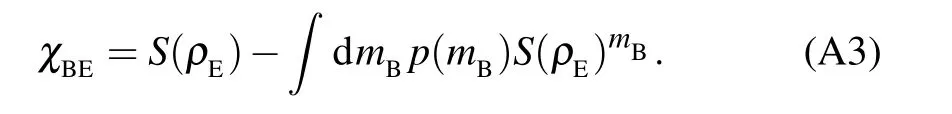
For the Gaussian-modulated coherent states，[7]χBEcan be simplified as follows:

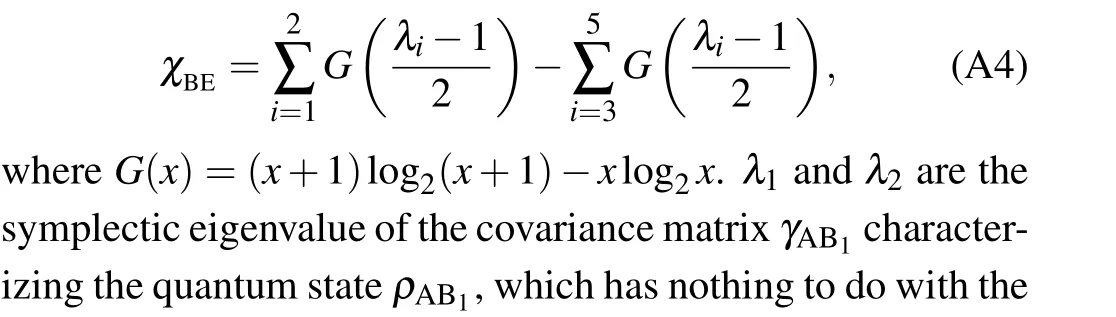
with the following parameters:[42]

As mentioned before，Δ(n)is a linear function related to privacy enhancement，which can be written as follows:

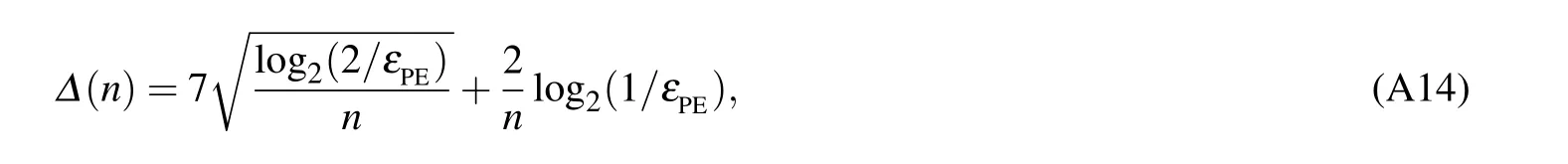
hereεPEdepicts the failure probability of the parameter estimation.