Photon blockade in a cavity–atom optomechanical system

Zhong Ding(丁忠) and Yong Zhang(张勇)

School of Science，Beijing University of Posts and Telecommunications，Beijing 100876，China

Keywords: photon blockade，photon-induced tunneling，cavity–atom optomechanical system

1. Introduction

Single-photon sources and single-photon detectors have great potential applications in the quantum information field，such as precision measurement， quantum cryptography， and quantum key distribution.[1，2]In recent years，it has been proposed that photon blockade(PB)effects，which describe a phenomenon that a single photon could block the transmission of other photons in some systems， can be exploited to prepare single-photon sources.[3–5]There are two general ideas regarding PB effects: (i)conventional PB(CPB)，which originates in the anharmonicity of the energy spectrum，[6]and(ii)unconventional PB(UPB)，which results from the destructive quantum interference between the different possible transition paths.[7]On the one hand， the CPB effect， which requires some kind of large nonlinearity，has been researched in various quantum systems， such as Kerr-type nonlinear cavities[8]and optomechanical systems.[9，10]The UPB effect， on the other hand， usually requires a large coupling strength between the two components that structure the different transition paths.Based on this theory， the UPB effect has also been observed in a coupled quantum-dot-cavity system，[11]double-cavity optomechanical systems，[12]and other systems.[13–16]Previous studies have been focused mainly on the single-photon blockade(1PB).Recently，the two-photon blockade(2PB)has been experimentally[17]and theoretically[18，19]investigated in various configurations， which could be used for two-photon sources. Furthermore， the photon-bunching effect， namely，photon-induced tunneling (PIT)， which means the probability of admitting subsequent photons is increased when there is one photon inside the cavity，[19]has also been explored in many systems.[20–23]

Great success has been achieved in cavity optomechanics in the quantum information field over the past decades.Cavity optomechanics is widely used in optomechanical oscillators， displacement sensing， Newtonian gravity detection，and other fields of quantum physics.[24]In addition， research attention has been given to the reaction effect of mechanical motion on the optical field， such as laser noise cooling，[25]optomechanical entanglement，[26]optomechanically induced transparency，[27，28]and PB.[9，10，29，30]Herein， we focus on studying the PB effect in a cavity–atom optomechanical system. By analyzing the resonance condition， we analytically optimize the parameter condition of the respective 1PB case.In addition，PIT usually appears more easily than a 2PB.Furthermore，by calculating the correlation functions，we find that a 2PB region would occur in the optomechanical system.

The rest of this paper is organized as follows. In Section 2， we discuss the physical model and investigate the Hamiltonian of the system. In Section 3， we analyze the eigenstates to obtain 1PB and optimize the parameters to obtain 2PB.The result can be confirmed by analytically solving the Schr¨odinger equation or numerically simulating the master equation. The atom-driving case is also discussed briefly.Conclusions are given in Section 4.

2. System and Hamiltonian

We consider a cavity–atom optomechanical system composed of a single-mode cavity field coupled to a two-level atom via a two-photon physical interaction，[31，32]as depicted in Fig. 1(a). The cavity is pumped by a classical laser with frequencyωdand amplitudeε. The interaction between an optical cavity and mechanical film in a cavity optomechanical coupling system is realized by photon radiation pressure.[33，34]The Hamiltonian of the model is(¯h=1)[34–39]

Fig. 1. (a) Sketch of the cavity–atom optomechanical system (cavity-driven)， with κ， γ， and γm being the cavity， atomic decay rates， and damping rate of the mechanical resonator，respectively. (b)Schematic energy-level structure of the system in the subspace with zero，one，two，and three excitations. (c)Transition pathways in the cavity-driven case.

3. Photon blockade in the cavity–atom optomechanical system

3.1. Analytical solution

In the weak driving limit，we can restrict the total photon number within the low-excitation subspace up to 3. Therefore， the wave function|ψ(t)〉can be expressed by the timeseparable state approximately as follows:[48]

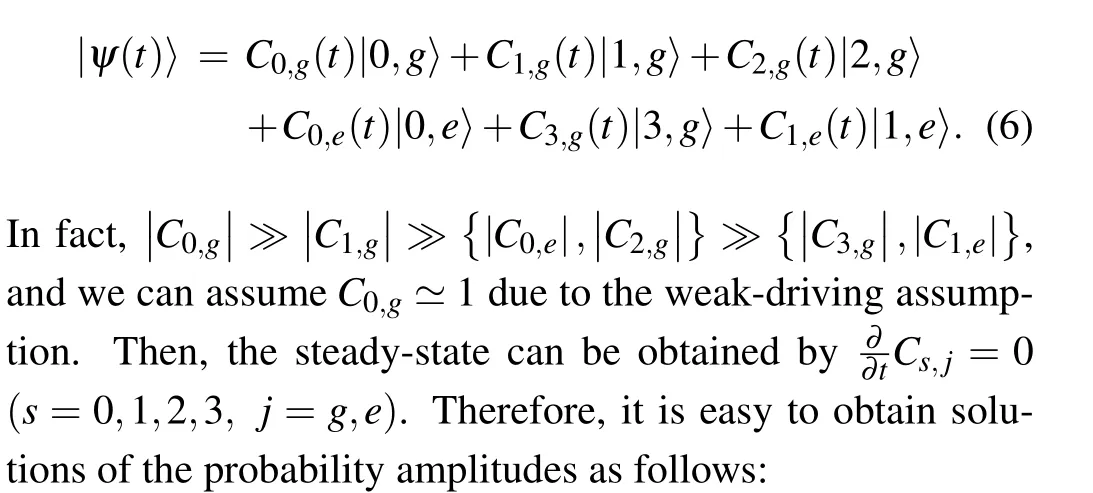
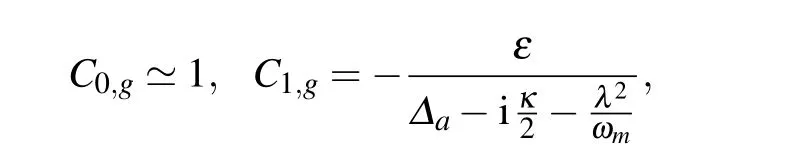
The PB effect can be estimated by the equal-time secondorder correlation functiong2(0)and the equal-time third-order correlation functiong3(0). Based on Eq.(7)， the steady-state correlation functions of the cavity can be analytically obtained by the steady-state solution of the Schr¨odinger equation:

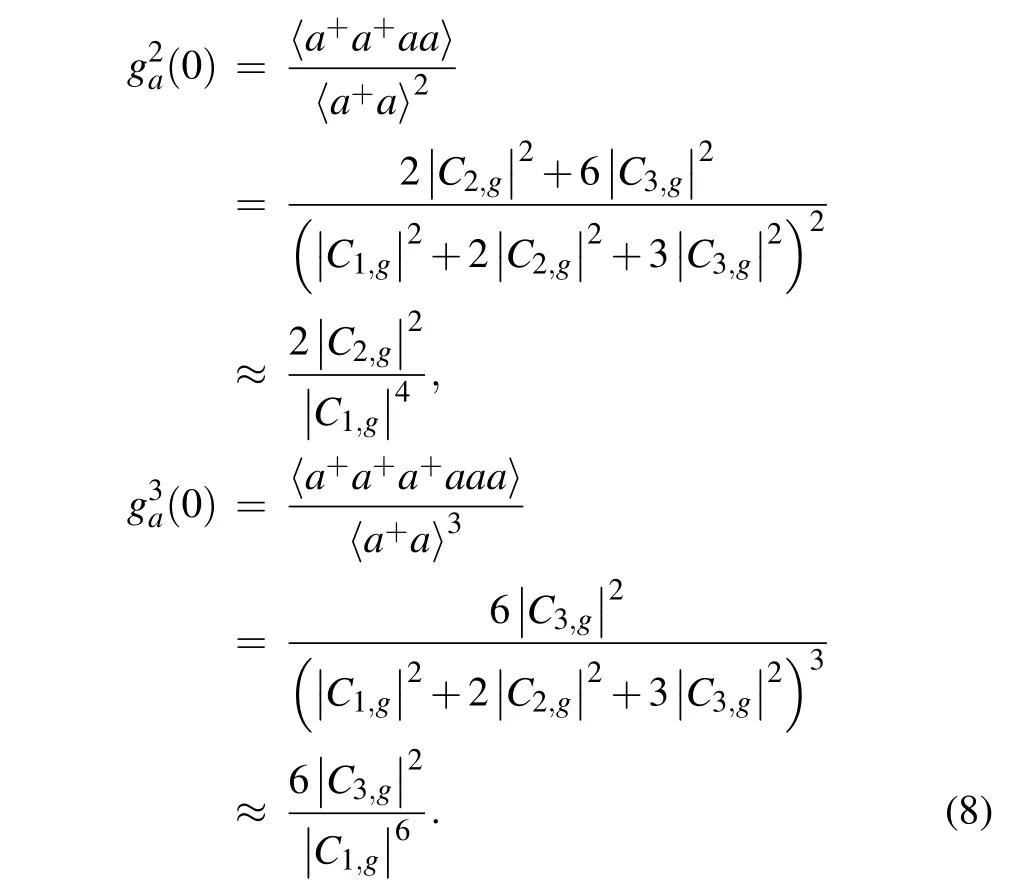
Note that if〈ˆn〉≪1(the average photon number)，wheng2(0)＜1， it indicates 1PB; wheng2(0)＞1 andg3(0)＜1，2PB occurs， which implies two-photon bunching and threephoton anti-bunching，g2(0)＞1 andg3(0)＞1 indicate typical PIT.[19]In the weak-driving case， the photon number is very small.

3.2. Numerical solution

However， we utilize the quantum master equation with the initial HamiltonianHto correctly account for the drivendissipative character of the system，which is also a method of exact solution:[49–51]

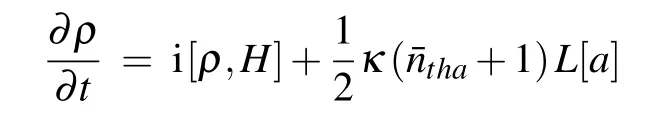
where the HamiltonianHis expressed in Eq. (2)，L[o] =2oρo+-o+oρ-ρo+oare Lindblad terms accounting for the arbitrary system operatoro;κ，γ，andγmare the cavity，atomic decay rates，and damping rate of the mechanical resonator，respectively; ¯nthx=[exp(¯hωx/kBTx)-1]-1，x={a，1，b}are the average thermal excitation numbers of the bath at temperaturesTaandT1(x={a，1})， and the mechanical thermal excitation number at the temperatureTb(x=b)， withkBthe Boltzmann constant.

In the system，we are concerned aboutg2(0)andg3(0)in the steady state， and must thus solve the master equation for the steady-state density operator by setting∂ρ/∂t=0. The exact numerical result is given by

However， there is an obvious deviation between the two methods in the higher-order correlation functions. This is because we neglect the influence of quantum jumps in solving the effective Hamiltonian.[18]

3.2.1. Single-photon blockade

3.2.2. Two-photon blockade

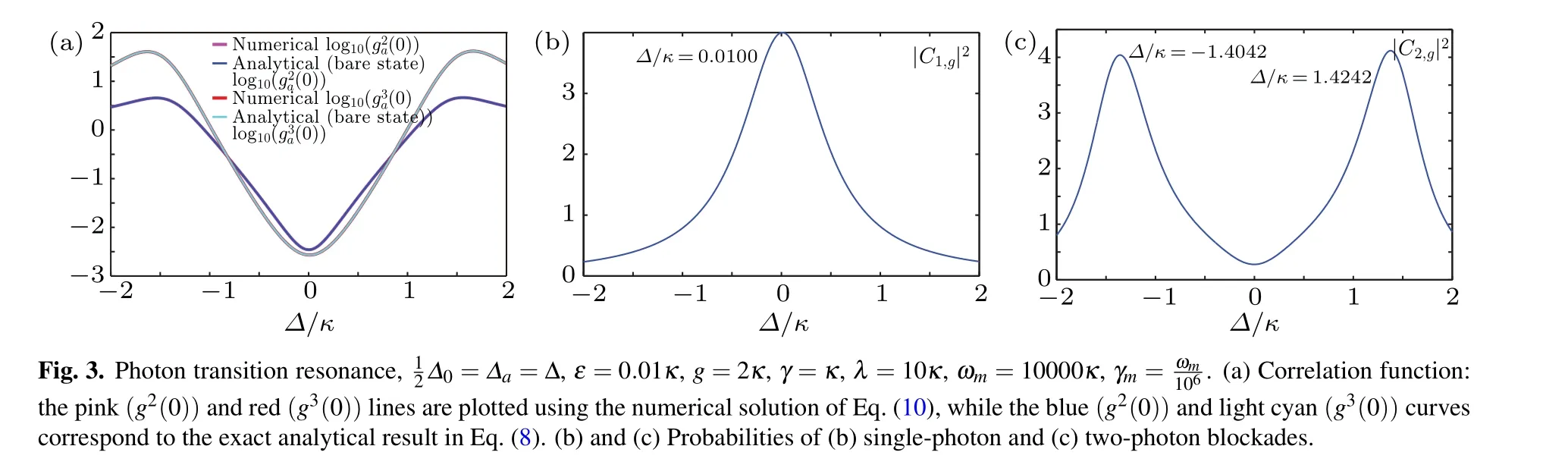
3.3. Discussion

We next consider the case of atom driving，which seems a good project by which to obtain the 2PB effect.[31]However，we calculateC1，g=0 in an analytical solution， which represents thatg2(0)andg3(0)are relatively large and that PIT appeared. Owing to the two-photon physical transition process，the judgment of the 2PB effect can rely on the criteriong4(0)，which is calculated by the master equation.In the cavity–atom system， 2PB may emerge because of the transition resonance(ω0=2ωa，|ε0〉→|ε2±〉，|ε0〉→|ε4±〉). However，our scheme could build a region of the 2PB effect under cavity driving.

Moreover， cavity optomechanics could also achieve the 2PB effect， but|C2|／=0 in this system， which means that the perfect 1PB effect could not be obtained. In other words，cavity optomechanics could not use interference to enhance the PB effect. Our system could use this phenomenon， which is briefly discussed in Subsection 3.2.1.

4. Conclusions

In summary，we have investigated the 1PB，2PB，and PIT effects in a cavity–atom optomechanical system. By analyzing the transition resonance，we find that the 1PB and PIT actions can be observed easily in the cavity–atom system，while 2PB is difficult to realize. Therefore，adding an optomechanical system could help us build a 2PB region. Moreover， we briefly discuss the PIT effect that may occur under atom driving. Our analysis results are obtained by solving the equations of motion for these probability amplitudes and are confirmed by solving the quantum master equation in the truncated Hilbert space.