Real non-Hermitian energy spectra without any symmetry

Boxue Zhang(张博学)， Qingya Li(李青铔)， Xiao Zhang(张笑)， and Ching Hua Lee(李庆华)

1School of Physics，Sun Yat-sen University，Guangzhou 510275，China

2Department of Physics，National University of Singapore，Singapore 117542，Singapore

Keywords: non-Hermitian physics，real energy spectra，non-Hermitian skin effect

1. Introduction

Non-Hermitian systems have recently inspired intense research efforts for their unconventional mathematical properties and physical robustness， such as enlarged topological symmetries，[1–8]exceptional point sensing，[9–15]quantized classical responses，[16]modified bulk–boundary correspondences，[17–32]unconventional entanglement entropy scaling，[4，33–39]enhanced Rabi oscillations，[26，40，41]and effective non-Hermitian curved space.[42，43]Yet， many of these exciting phenomena are often difficult to probe experimentally due to their intrinsically unstable nature from complex eigenenergies. While real eigenenergies can be symmetryenforced，i.e.，through PT-symmetry，[44–51]doing so is incompatible with realizing many of the most exotic non-Hermitian phenomena.[20，52–66]

In this work， we carefully investigate how the non-Hermitian skin effect (NHSE)[67–73]can also enforce real non-Hermitian spectra， even for lattices whose couplings and momentum-space descriptions do not admit any obvious symmetry. The NHSE has been heavily associated with modified bulk-boundary correspondences[17，39]and，in our context，implies that a system can robustly possess real spectrum in the presence of a boundary， even though its bulk is unstable with complex eigenenergies.Physically，this is because the directed amplification in a NHSE lattice can be stabilized by the interfering wavepackets from a boundary or spatial inhomogeneity，a mechanism that is unrelated to conventional symmetry protection.

We elucidate this route towards real eigenspectra in terms of the inverse skin depth[17，74]κ， which is an additional degree of freedom that mathematically takes the role of imaginary momentum. It physically controls the accumulation and interference of skin states at a boundary， and mathematically replaces the Bloch description of the lattice by an effective surrogate[74]model that can look completely different.Specifically，we shall show that in a bounded lattice，the reality of the spectrum is only destroyed by a spontaneous symmetry breaking process that can occur much later than the explicit symmetry breaking at the Bloch level.

2. OBC vs. PBC spectra

We first review and distinguish the approaches for computing the eigenenergy spectrum under open vs. periodic boundary conditions(OBCs vs. PBCs). Given a generic non-Hermitian HamiltonianH(k)，PBC eigenenergies ˜Eand OBC eigenenergies ¯Eare obtained very differently. To find the set ofE ∈˜E，we simply solve for eigenenergiesEsuch that characteristic polynomialP(E，k) = Det[H(k)-EI] = 0， wherek ∈[0，2π). However， under OBCs， translation invariance is broken， and in general the spectrum is not indexed by real momentumk. Instead， the OBC spectrumE ∈¯Eis given by eigenenergiesEthat solve

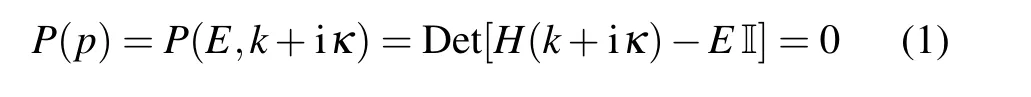
and are degenerate in bothEandκ. Hereκis the imaginary part of the complexified momentump=k+iκthat also represents the inverse decay length(skin depth)of eigenstates viz. eipx～e-κx， i.e.， taking the role of a length scale[75，76]not present in Hermitian systems. Thisκdegeneracy is required because OBC skin eigenstates have exponential spatial profiles，and we need a superposition of two of them with identicalEandκto satisfy OBCs at two arbitrarily separated boundaries (as we interpolate between OBCs and PBCs， we observe a peculiar scaling behavior of the corresponding effectiveκ[98]). In general，we writeκ=κ(k)to emphasize itsk-dependence，andp=k+iκ(k)is known as the generalized Brillouin zone(GBZ).[17，18，18，19，21–23，78]H(p)=H(k+iκ(k))is also referred to as the surrogate Hamiltonian，which is used instead of the original Bloch HamiltonianH(k)in computing topological invariants(however，the topological eigenenergies themselves fall outside of the purview of our prescription，because they are isolated solutions that are not adiabatically connected to any Bloch solution)[80–82]and spectral properties under OBCs.

Note that the above prescriptions for the OBC and PBC eigenenergies cocide in the case of Hermitian lattices， since aspcycles through real values [0，2π)， every value ofElies on the real line and will be visited at least twice， both withκ=Im(p)=0.

2.1. Minimal model with different OBC vs. PBC spectra

As a concrete demonstration， we consider a minimal model withHmin(z) =z++Az2， wherez= eik. In real space， it contains two symmetric nearest neighbor (NN)hoppings and another uncompensated next-nearest-neighbor(NNN) hopping:Hmin= ∑x|x+1〉〈x|+|x〉〈x+1|+A|x+2〉〈x|. Clearly， its PBC spectrum is given by ˜E=2cosk+Ae2ik，and is entirely complex unlessA=0，as plotted as the thick red curve in Fig.1 forA=2. However， large segments of its OBC spectrum lie on the real line，as shown by the black dots.

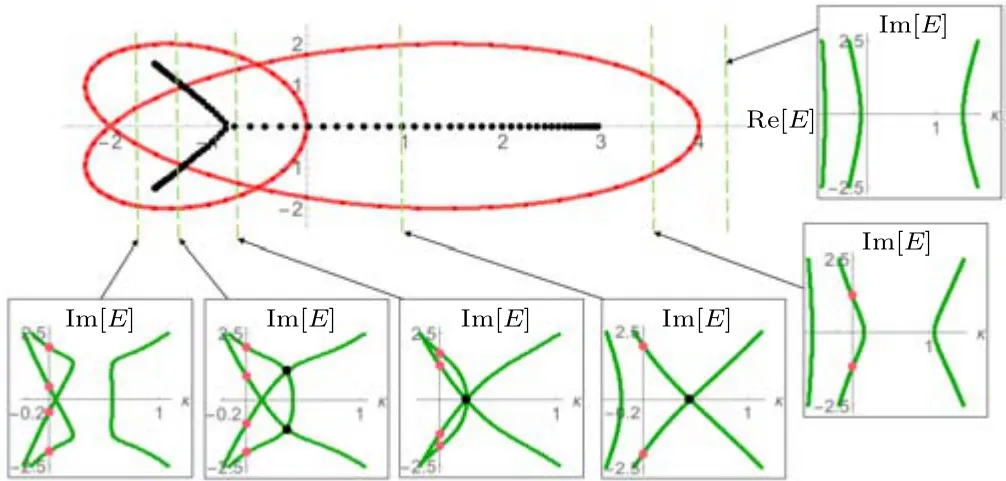
Fig. 1. Real OBC vs. real PBC spectra in terms of the symmetry of κ(E)solutions. Shown are the OBC(black)and PBC(red)spectra of the model Hmin with dispersion E(z)=z+z-1+2z2; the inset plots show Im(E(z))as a function of κ =-log|z| (green κ curves) at various fixed Re(E(z))slices. PBC eigenenergies (red dots) correspond to (Re(E(z))，Im(E(z)))consistent with κ =0，and OBC eigenenergies(black dots)correspond degeneracies in both κ and E(z)(green curve intersections). In particular，we have real OBC eigenenergies when the green curves intersect at Im(E)=0，which often occurs even when the PBC eigenenergies are non-real.

Below，we explain how one can visually derive the OBC and PBC spectra. We turn to the plots ofκsolutions vs.Im(E)， for fixed Re(E) slices. Going from large to small Re(E)，we find that PBC eigenenergies(red)first appear when we pass Re(E)=4， followed by OBC eigenenergies (black)after Re(E)=3. In the green Im(E) vs.κplots， it is apparent that PBC eigenenergies appear when the greenκsolution curves crossκ=0，while OBC eigenenergies only appear when theκcurves intersect. This is exactly what was prescribed earlier-κ=0 gives the PBC spectrum， whileκdegeneracies give the OBC spectrum. As Re(E) decreases further，additional PBC winding loops appear，and they correspond to additional 0 crossings ofκfrom the green curve that is emerging from smallκ.At Re(E)≈-0.79，that green curve goes over the original blackκintersection，thereby splitting it into two black intersections.That corresponds to the two black OBC branches away from the realEline. Finally，when these twoκintersections gap out at sufficiently negative Re(E)，the OBC eigenenergies disappear.

All in all，we see that real OBC eigenenergies correspond to intersections of theκcurves at Im(E)=0， which can exist even if PBC eigenenergies are already complex，i.e.，if theκcurves crossκ=0 at Im(E)／=0. As such， the breakdown of the reality of the spectra can be understood as the breaking of the symmetry of theκcurves. In the following we detail the conditions to have non-real PBC and OBC spectrum， and it is clear that the later is often harder to achieve.While a non-real PBC spectrum only requires theκcurves to have asymmetric zero crossings，which are almost guaranteed in a system without PT symmetry， a non-real OBC spectrum requires that symmetry to be spontaneously broken， i.e.， broken at the level of“extrema”corresponding to the intersection points. Tellingly， it is often much harder to have asymmetricκintersections rather thanκzero crossings，and that explains the relative robustness of real OBC spectra compared to real PBC spectra.

3. Parameter spaces for real eigenenergies

We next present the parameter space for real OBC spectra for several paradigmatic models. It has to be emphasized that almost all eigenenergies (under both OBCs and PBCs) fundamentally depend on the form of the dispersionP(E，p)，and only indirectly on the form of the Hamiltonian.The exceptions are the eigenenergies of isolated topological modes，which are protected by bulk eigenstate topology， but we will not focus on them here.

3.1. Separable energy dispersions P(E，p)

We first discuss separable dispersions，namely，those withP(E，p)=F(E)+G(p)， whereF(E) is a function ofEandG(p) is a Laurent polynomial ofz= eip. As long asG(p)gives an OBC spectral curve that does not contain branches，we can in principle achieve a real spectrum by modifying the model such thatF(E)conformally[85]maps the curve onto the real line. For this reason， the non-Hermitian SSH model and its variants can all possess real spectra.[17，85，86]

3.1.1. Single-component Hamiltonians

We start with the single-component Hamiltonians，whose characteristic polynomials are simply given byP(E，p) =H(p)-E. As discussed above，cases with only two NN hoppings are trivial，since they are always reducible to the equivalence class ofH(z)=z+z-1. As such，the minimal nontrivial case is the 3-hoppings modelHmin(z)， which we just examined. There are two ways to generalize to the next level of sophistication through a fourth hopping term，namely，

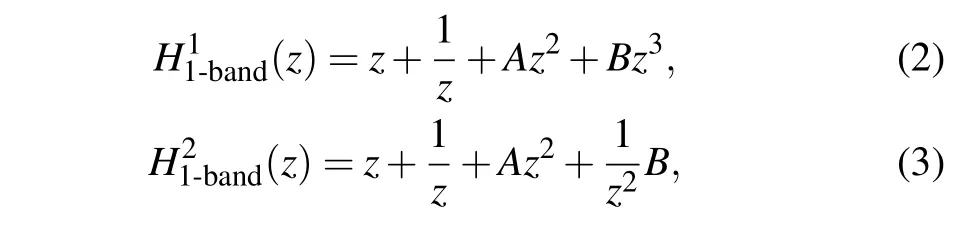
wherez= eip. These two models capture all the possibilities for Hamiltonians with hoppings spanning four sites， up to reflection and translation symmetry. Note that for singlecomponent models， the onsite term is just a trivial constant.Also， all meaningful models must possess both left and right hoppings， since otherwise the OBC spectrum will collapse onto a single point.[87，88]

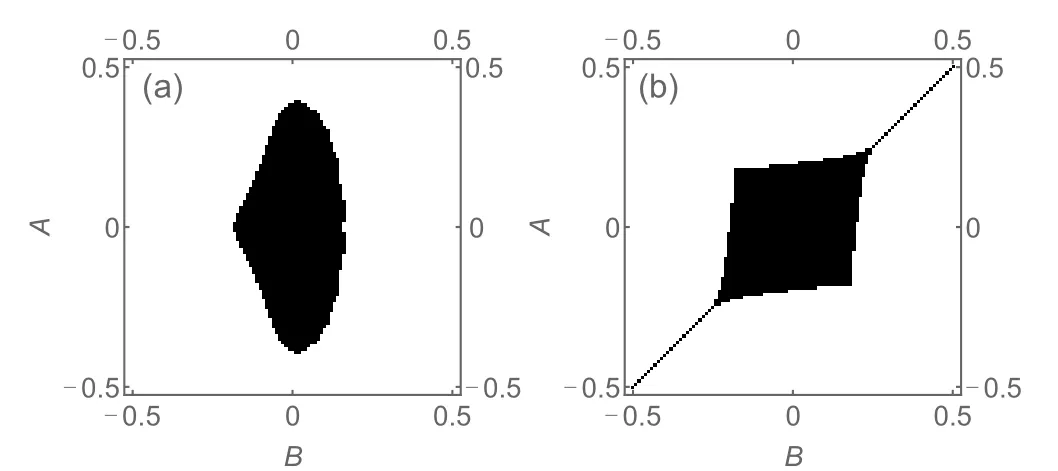
Fig.2.Regions of the parameter space with real OBC spectra(black)for the following 2-component models: (a)H11-band and(b)H21-band. In(b)，models with A=B also trivially result in real spectra. The numerical threshold is Max|Im(E)|＜ε =10-6.

As we can see from Figs. 2(a) and 2(b)， there exists a rather large(black)region in the(A，B)parameter space where the spectra still remain real，despiteAandBmanifestly breaking any possible symmetry. Indeed， theAz2+Bz3term ofH11-band(z) gives rise to robustly complex eigenenergies under PBCs， even though it can still give a real spectrum forAas large as 0.35 (Fig. 2(a)). ForH21-band(z) with dispersion 2cosp+Ae2ip+Be-2ip， the OBC spectrum is trivially real forA=B， but still remains real for a large parameter region away from that(Fig.2(b)). Physically，this is so because interference from waves reflected off a boundary are sufficient in preventing a wavepacket from being amplified indefinitely.

3.1.2. Two-component Hamiltonians

In 2-band models，we have

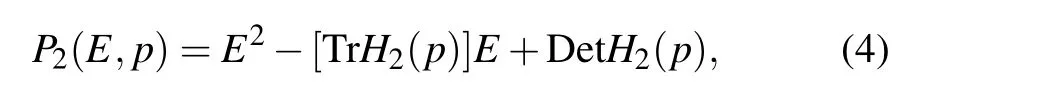
such that separable dispersions correspond to Hamiltonians withp-independent traces，which can occur when the diagonal terms are either zero or constant. Physically，this corresponds to the absence of homogeneous same-sublattice net hoppings across different unit cells.

In this case of constant trace，the dispersion is essentially determined byF(E)=-G(p)=DetH2(p)，directly generalizing the case of 1-component models upon the conformal transformE →E2-[TrH2]E.The only difference is thatG(p)now contains products of matrix elements ofH2(p)， and as such is usually a higher-order polynomial describing OBC spectra with no analytic solution. While a higher-orderG(p) can result in a more branched and hence complex OBC spectrum，with appropriate model design，there can still be larger parameter regions with real OBC spectra，see Fig.3.

For instructive purposes， we first study the 2-component model with almost trivial NHSE:

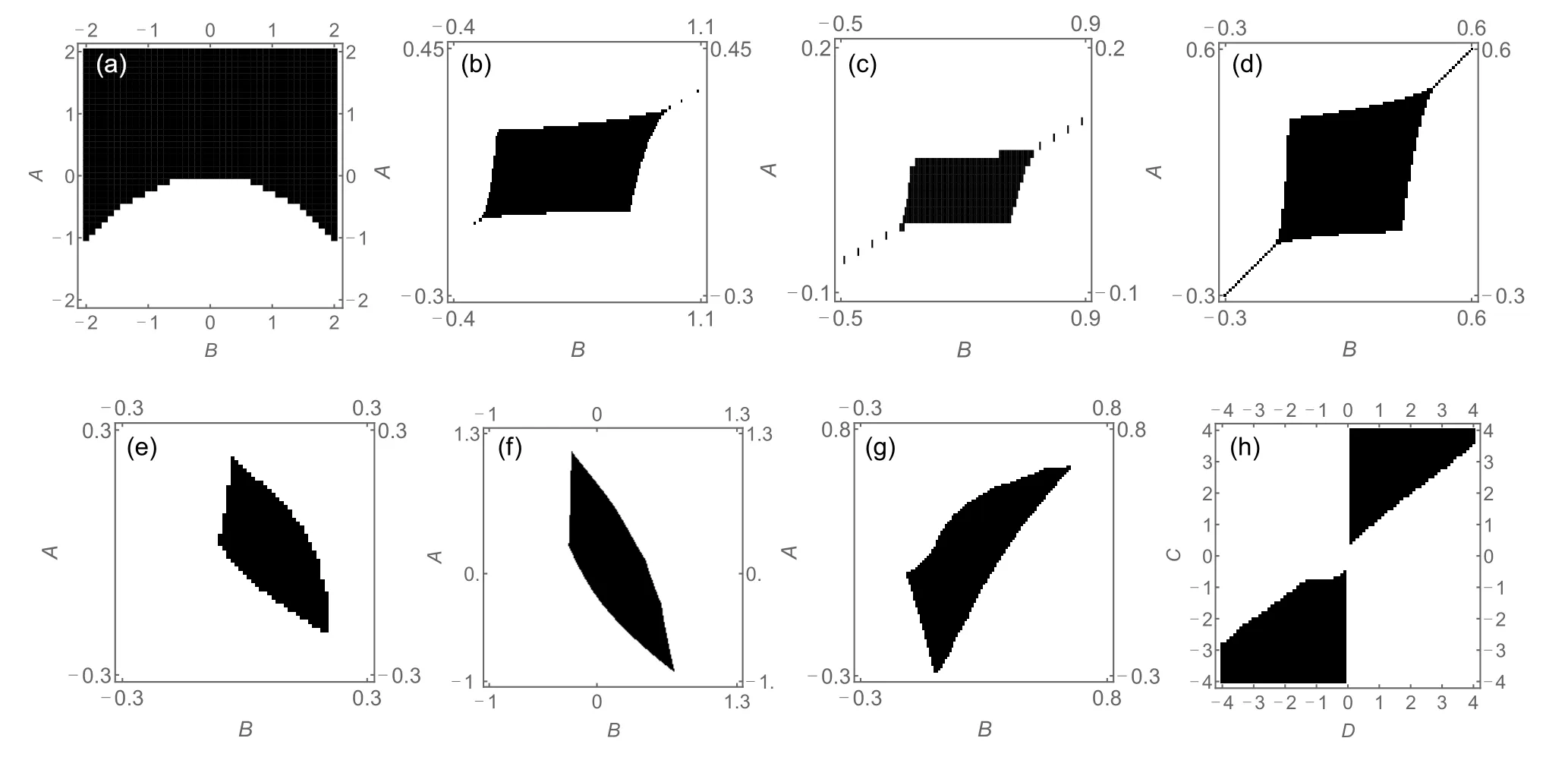
Fig. 3. Regions of the parameter space with real OBC spectra (black) for the following 2-component separable models: (a) H02-band; (b) H12-band with C=2，D=3; (c)H12-band with C=1/2，D=1; (d)H12-band with C=2，D=2; (e)H22-band with C=2，D=3; (f)H22-band with C=2，D=1;(g)H32-band with C=2，D=2;(h)H32-band with A=0.1，B=0.1. The numerical threshold is Max|Im(E)|＜ε=10-6. Note that the PBC spectra of all of these models are complex.

3.2. Inseparable energy dispersions P(E，p)

We next consider more sophisticated dispersions which contain products ofEandz= eik. In general， they are not analytically tractable， although their spectral graph structure can often still be heuristically predicted.[85]In this work， we shall limit ourselves to 2-component models. From Eq. (4)，those with inseparable dispersions correspond to those withp-dependent traces， i.e.， those with same-sublattice hoppings across unit cells.

3.2.1. Analytically tractable examples

First， we introduce an inseparable case whose condition for real spectrum can still be analytically derived. Consider

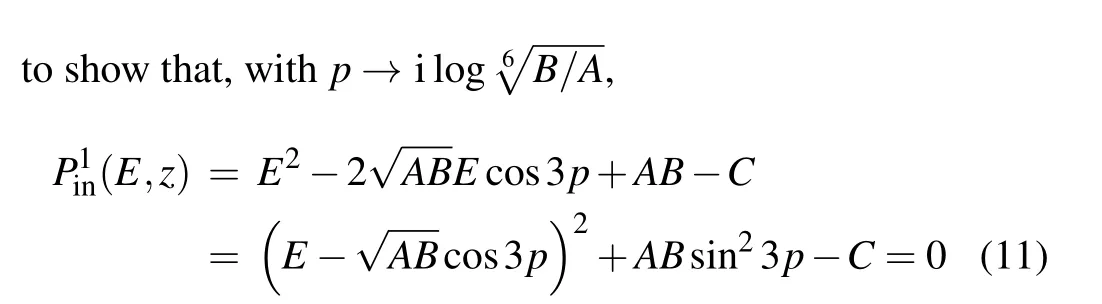
admits realEsolutions generated by realpas long as 0≤AB ≤C.Outside of this regime，complex pairs ofEsolutions appear(Fig. 4(a))， leading to non-real spectra. Figure S1 shows the boundary behaviour of spectra from real to non-real as the parameter varies. This criterion 0≤AB ≤Centails that the real spectrum hinges on the presence of nonzero coupling， and is numerically verified in Fig.4(a).

Next， we introduce another Hamiltonian which admits real spectrum for parameters that make it separable:

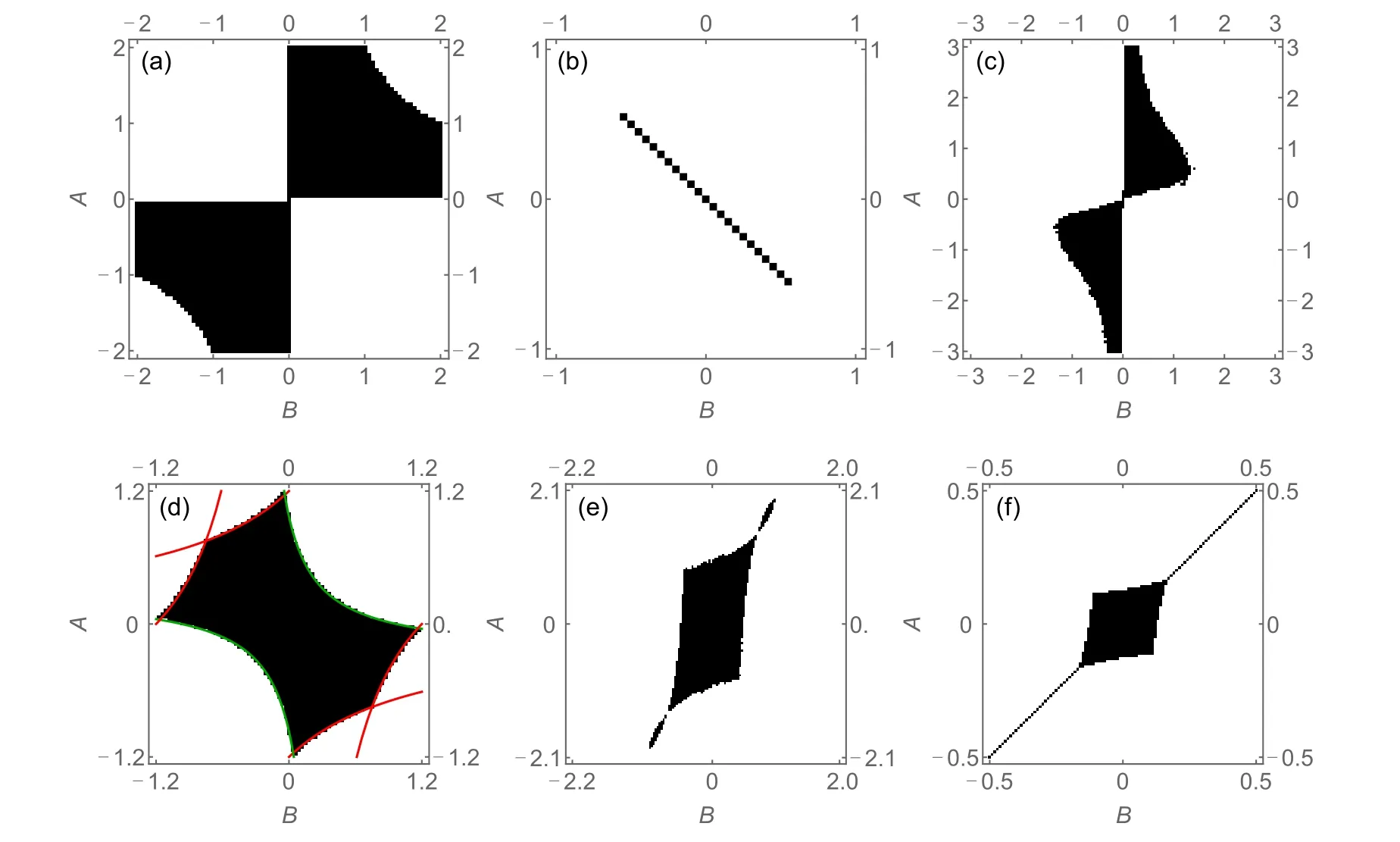
Fig. 4. Regions of the parameter space with real OBC spectra (black) for the following 2-component inseparable models: (a) H1in(z); (b) H2in(z);(c) H3in(z); (d) H4in(z) with the regime boundary approximately depicted by curves (0.28+A)(0.28+B) = 0.35 and its reflection across line A=-B(green)，1.2=A(-0.8B+1)and its reflection across line A=-B plus further reflection across line A=B(red);(e)H5in(z);(f)H6in(z). The system length is L=30 for all and the numerical threshold is Max|Im(E)|＜ε，where ε =10-5 for(c)and ε =10-6 for the other cases.

3.2.2. More general examples

Next，we introduce a few more models whose propensity for real OBC spectra cannot be predicted through any simple way:

LikeH1inof Eq. (9)， the modelH3incontains constant offdiagonal couplings. However， despite its simple algebraic form，it is not analytically tractable，and in fact behaviors completely differently fromH1in，and in fact the other models too.

The real spectrum parameter region ofH6inis an interesting intersection of a diagonalA=Bline segment， and a smaller extended region. These two parameter subregions have different origins. For the former， the OBC spectrum is real because the PBC spectrum is also real;largerA=Bcloses the band gap and releases complex eigenenergies. For the latter，the PBC spectrum is always complex(example in Fig.S2)，but an open boundary creates sufficient interference to stop indefinite amplification，leading to a completely real spectrum.

4. Discussion

In this work，we have seen that real non-Hermitian OBC spectra are generically more robust than real PBC spectra.This can be explained in terms of the inverse skin depthκ(E)solutions curves–while the PBC spectrum becomes complex onceκ(E)／=0 at ImE／=0，a complex OBC spectrum requiresκ(E)curves to intersect at ImE／=0，which is a more demanding condition. While there exists a very general electrostatics approach[89]that returns possible parent Hamiltonians for any desired real OBC spectrum and skin localization， this work showcases particularly simple ansatz models that have the benefit of being as local as possible.

The discovery of these Hamiltonians with real spectra complements existing efforts towards the design of stable non-Hermitian system， particularly the PT-symmetry route. With a greater set of ansatze models that are not symmetry constrained，a larger variety of interesting non-Hermitian physics，i.e.，non-Hermitian skin clusters and pseudogaps[90–92]can be realized not just with enhanced stability，but also with generically non-reciprocal platforms such as circuits with MOSFETs or operational amplifiers.[20，46，59，93–97]Yet， the NHSE is not guaranteed to yield real spectra，and in Appendix A，we have also listed down models which failed，to aid further search efforts.

Appendix A:Inseparable energy dispersions not giving real spectra

While the main text had discussed various models with real spectra despite having no favorable symmetries，it is also important to record models where thisdoes not occur. As discussed， NHSE-induced real spectra depend on the algebraic properties of theκ(E) curves， and it is instructive to list the models where they do not behave favorably as such.

For instance， the following deformations ofH1in(z) have no real spectra:

Models with non-symmetric hopping systems:

Acknowledgments

X.Z.is supported by the National Natural Science Foundation of China(Grant No.11874431)，the National Key R&D Program of China (Grant No. 2018YFA0306800)， and the Guangdong Science and Technology Innovation Youth Talent Program(Grant No.2016TQ03X688).