严寒地区混凝土重力坝变形行为分析与预测模型

袁冬阳，顾冲时，顾 昊

（1.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学 水利水电学院，江苏 南京 210098；3.河海大学 水资源高效利用与工程安全国家工程研究中心，江苏 南京 210098；4.河海大学 农业科学与工程学院，江苏 南京 210098）

1 研究背景

大坝是保障江河安澜、促进国民经济增长与区域稳定的重要基础设施，伴随筑坝工艺的发展，我国混凝土坝建设在筑坝高度、数量与规模等方面取得了举世瞩目的成就［1-2］。运行期混凝土坝不仅要长期承受静、动循环荷载作用，还面临着气候变暖与突发性自然灾害等多重风险威胁［3-5］。工程一旦失事，将对下游人民生命安全、区域稳定与水生态安全等造成无法挽回的巨大损失。为保障工程长效健康服役，大坝健康诊断和安全管控理论与方法已成为当前坝工领域研究的前沿科学问题［6］。变形作为最能直观反映混凝土坝综合服役性态变化的重要监测量，其蕴含了坝体-坝基复杂非线性动力系统在内部材料性能与外部环境荷载双重演变作用下的结构响应信息，合理的变形行为分析与预测模型对于定量解析环境荷载变化对大坝服役性态的影响效应、实时判诊大坝健康态势与预测未来运行行为具有重要意义［7-9］。

根据建模方法，混凝土坝变形行为分析与预测模型可分为统计模型、确定性模型和混合模型三大类［10-11］，其中，统计模型是通过数理方法挖掘大坝变形与其解释变量间函数关系的因果分析模型，因具有结构形式简单、计算高效等优点，在大坝变形行为分析与预测中取得了广泛应用与长足发展［10-12］。逐步回归（Stepwise Regression，SR）［11］、多元线性回归（Multip le Linear Regression，MLR）［13］等是坝工领域最常用的变形行为分析与预测方法，但此类方法难以有效解决解释变量间的多重共线性问题，易影响模型的建模精度与稳健性［2，12］。近年来，随着人工智能技术的发展，基于机器学习算法的应用研究已成为当前大坝变形行为分析与预测模型研究的热点，并取得了大量的有益成果。Kao等［14］采用人工神经网络（Artificial Neural Network，ANN）构建了某拱坝变形预测模型，并比选了不同神经网络模型的优缺点与适用性；范千等［15-16］率先验证了极限学习机（Extreme Learning Machine，ELM）在大坝变形预测研究中的有效性，并针对ELM可能出现的过拟合问题引入结构风险最小化原则加以改良；苏怀智等［5，17］利用理论完备、泛化性能强的支持向量机（Support Vector Machine，SVM）分别构建了大坝变形预测与预警模型，并在分析SVM 超参数选取对模型性能影响的基础上提出了可行的优化策略；Dai等［18］基于随机森林回归（Random Forest Regression，RFR）剖析了变形解释变量间的相关性，并据此构造了优化的变形预测模型；Liu等［19］应用长短期记忆网络（Long Short-Term Memory，LSTM）构建了某拱坝变形预测模型，并检验了模型的预测精度与长期预测性能；任秋兵等［20］基于门控循环单元（Gated Recurrent Unit，GRU），提出了融合单测点时序相关性和多测点空间关联性的大坝变形动态监控模型。此外，Li等［21］、Wei等［6］融合信号处理、时序分析与机器学习等多元分析方法，进一步拓展了变形预测模型的建模手段。与此同时，混凝土坝变形机理研究也取得了一定的进展，如Wang等［22］通过分析某特高拱坝在高水位稳定期坝体径向位移向下游侧持续增大现象的成因，提出了考虑静水荷载滞后效应的变形预测模型；Hu等［23］通过数值仿真模拟裂缝开度对大坝变形的影响，提出了考虑裂缝开度的变形预测模型；Tatin等［24］将坝体视为多个一维介质沿坝高方向的集成体，提出了考虑水温分布与大坝厚度的变形预测模型。就严寒地区混凝土坝变形行为分析与预测研究而言，吴艳等［25］采用传统统计模型原理，定量分析了环境荷载变化对寒旱区某碾压混凝土坝变形的影响效应；陈波等［26］提出了考虑气温滞后与削减效应的寒区混凝土坝变形预测模型，并以某混凝土拱坝为例验证了所提模型的预测性能。

考虑到严寒地区环境温度变幅大，而坝体混凝土温度场本质上受边界温度变化控制，本文采用实测边界温度作为温度因子，构建了基于实测边界温度的严寒地区混凝土重力坝变形行为分析模型。同时，为充分挖掘变形及其解释变量间复杂的非线性因果函数关系以提升模型的预测性能，引入一种在继承SVM良好学习能力和泛化性能基础上兼备训练高效优点的新型机器学习算法TSVR［27］，并结合WOA［28］对其参数优化求解，据此提出了基于优化TSVR的混凝土重力坝变形预测模型。以高纬度严寒地区某混凝土重力坝实测水平位移为例，结合所建变形行为分析模型剖析了该坝某表孔溢流坝段坝顶变形行为不协调的成因，研究成果对深入认识寒区混凝土坝服役性态与合理诊断大坝服役安全具有一定的理论意义和借鉴价值；同时，基于优化TSVR的预测模型可有效挖掘大坝变形及其解释变量间复杂的非线性函数关系，且具有出色的变形拟合与预测性能，为高精度预测大坝变形提供了一种新的技术手段。

2 基于实测边界温度的混凝土坝变形行为分析模型

混凝土坝变形是由静水荷载与温度荷载周期循环作用引发的可逆变形，和碱骨料反应、冻融循环与节理裂隙发展等可能导致大坝安全裕度降低的时变效应造成的不可逆变形组成［6，11，29］，如图1（a）所示。根据温度因子的选取，混凝土坝变形行为分析模型可分为静水-季节-时间（Hydrostatic-Seasonal-Time，HST）和静水-温度-时间（Hydrostatic-Thermal-Time，HTT）模型两大类［7，29］。对于运行期水化热已完全散发的混凝土坝，坝体混凝土温度随季节演变而变化，故HST模型常采用谐波函数模拟热变形。然而，HST模型中谐波函数仅能刻画热变形的长期变化特征，难以有效揭示环境温度年际差异与短期动态波动引发的热变形细节特征，因此，HST模型对修筑于环境温度动态波动幅度大的严寒地区的混凝土坝变形行为分析能力尚显匮乏。相反，HTT模型常采用坝体混凝土与基岩温度测值计算热变形，但该模型存在难以有效选取合理表征坝体混凝土温度场的温度测值的困难，且可能因引入较多的温度因子导致模型结构复杂甚至引发维数灾难［30］。

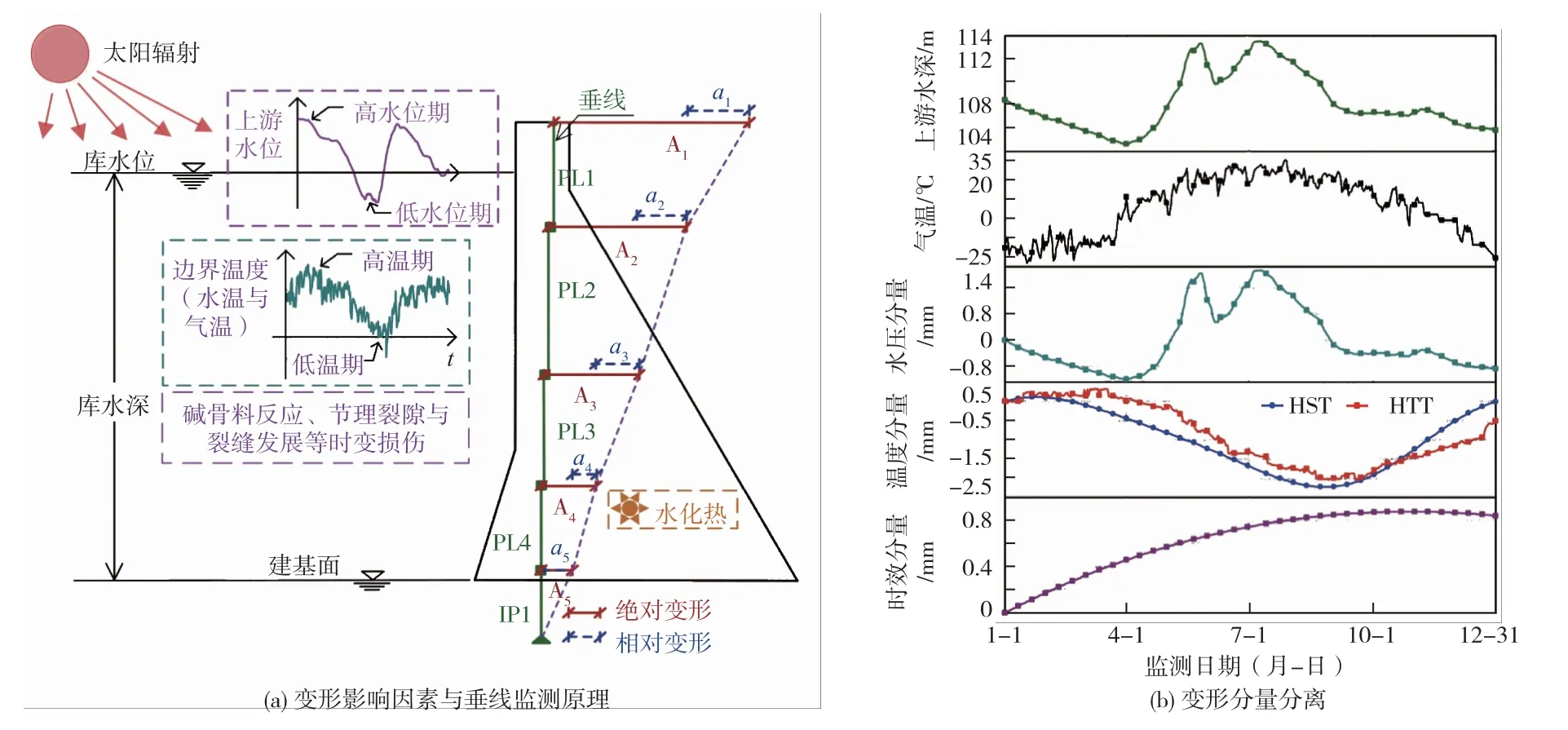
图1 重力坝水平位移机理示意

考虑到运行期混凝土坝温度场本质上受边界温度（即气温和库水温）变化控制［11］，故本文采用实测边界温度模拟热变形，其既可避免引入过多的解释变量导致模型结构复杂，又能有效弥补HST模型对热变形解译能力不足的缺陷。据此，构建的混凝土重力坝变形行为分析模型可表述为

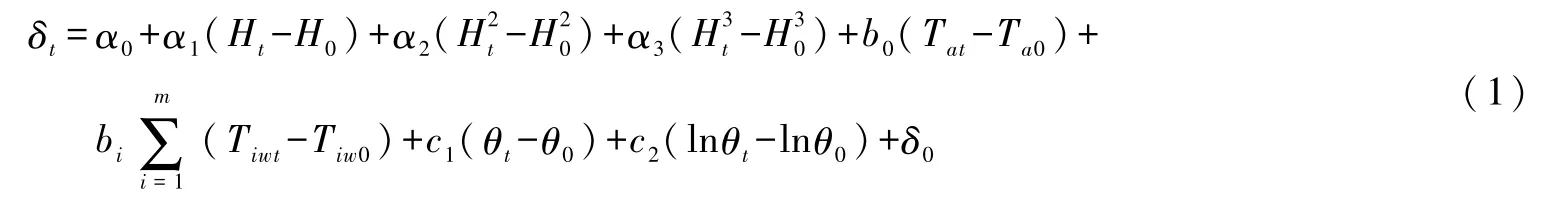
式中：α0为常数；δ0为建模序列初始日的实测变形；Ht、H0分别为监测日与建模序列初始日的库水深；Tat和Ta0分别为监测日与建模序列初始日的气温；Tiwt和Tiw0分别为监测日与建模序列初始日第i支库水温温度计的测值；α1—α3、b0、bi、c1和c2为统计系数；i为库水温温度计个数；θt＝t/100、θ0＝t0/100，t与t0分别为监测日与建模序列初始日距始测日的累计天数。

本文采用最小二乘法［11，31］求解式（1）中模型的系数，进而分离出水位、温度等主要环境荷载变化引起的水压、温度与时效变形，由此从宏观层面上量化分析环境荷载变化对混凝土坝变形行为的影响。

3 基于优化TSVR的混凝土坝变形预测模型

虽然最小二乘法可求解式（1）中模型的系数并分离出变形分量，但该方法所建模型的预测精度欠佳。为解决上述问题，本文结合式（1）所述的混凝土重力坝变形及其解释变量间的因果关系，引入Peng［27］于2010年基于孪生支持向量机（Twin Support Vector Machine，TWSVM）思想提出的一种适用于回归分析的新型机器学习算法TSVR构建混凝土坝变形预测模型。同时，为避免盲目选取TSVR参数对建模精度与泛化性能的影响，提出了基于WOA优化的TSVR。

3.1 TSVR基本原理TSVR算法的内核是寻找训练样本的一对不平行的不敏感上、下界函数以确定回归模型，如图2所示。相比SVM，TSVR通过求解两个较小规模的二次规划问题，其在发挥与SVM相当建模性能的同时具有更高的训练效率［27，32］。相关研究指出，TSVR 的训练耗时仅为SVM 的1/4［27，33］。

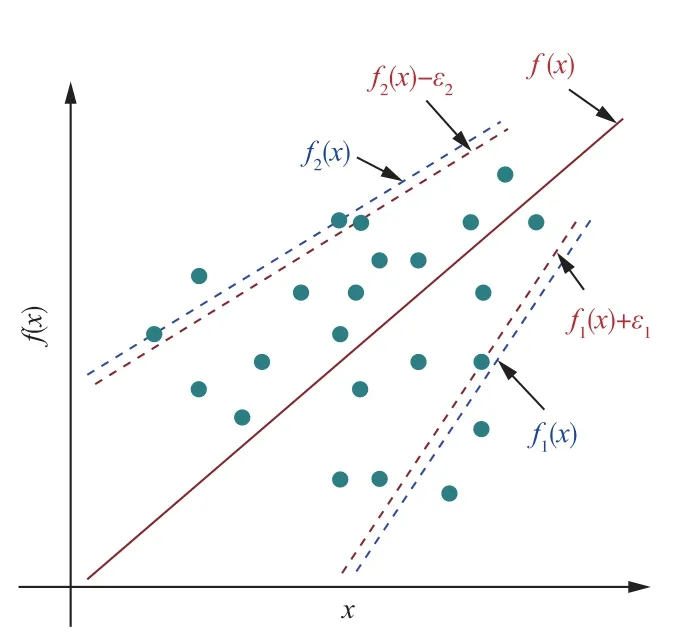
图2 TSVR结构示意

用以确定不敏感上、下界函数，进而可构造回归模型

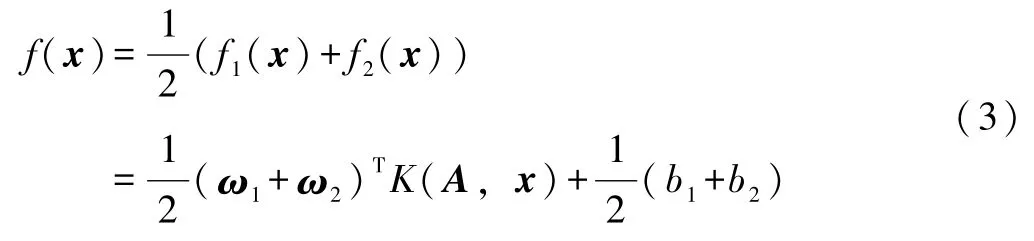
式中：ω1、ω2为权值向量；b1、b2为偏置；K（·，·）为核函数，其直接决定算法的高维特征空间与非线性转换。本文选取具有良好非线性映射能力的径向基函数（Radial Basis Function，RBF）作为核函数，即

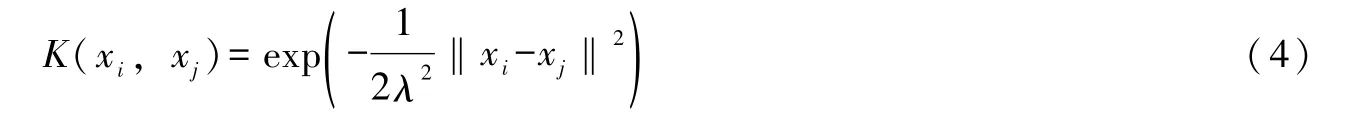
式中λ为RBF核宽度参数。

式（2）中函数的确定可通过求解下述一对凸二次规划问题

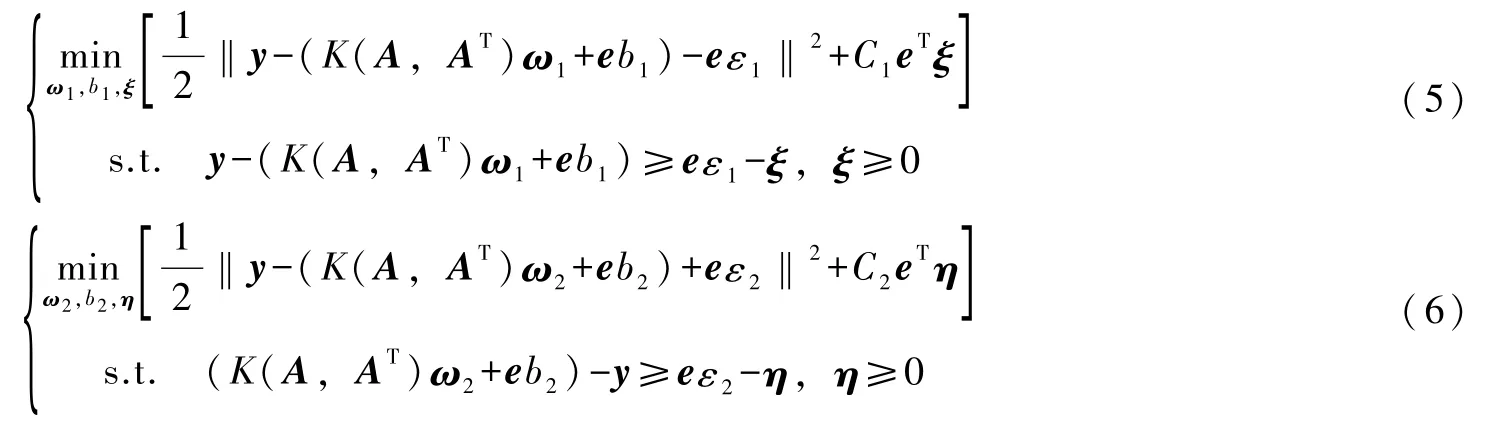
式中：C1，C2＞0为惩罚参数；ε1，ε2＞0为不敏感损失函数参数；ξ和η为松弛变量；e为m维全1列向量。

对式（5）引入非负拉格朗日乘子向量α＝（a1，a2，…，am）和γ＝（γ1，γ2，…，γm），其可改写为

结合Karush-Kuhn-Tucker（KTT）条件可得

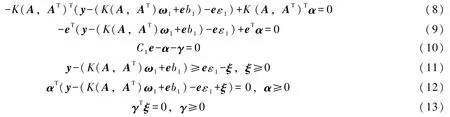
由式（10）与式（13）可知

结合式（8）和式（9），可得

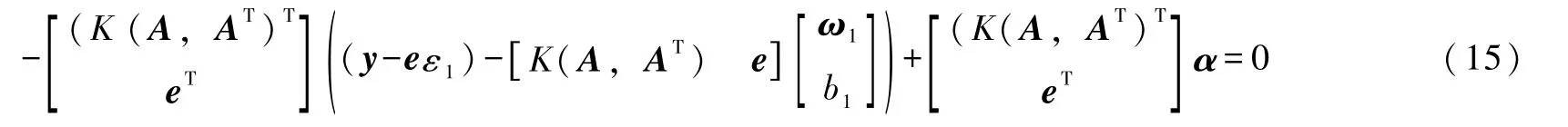
令H＝［K（A，AT） e］且f＝y-eε1，结合式（15）可得f1（x）的解为

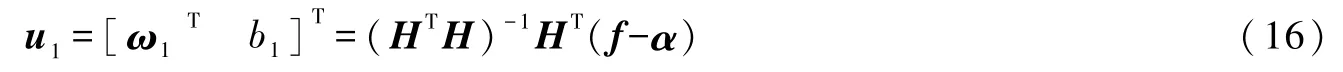
将式（16）与KTT条件带入式（7），可得到式（5）的对偶优化问题

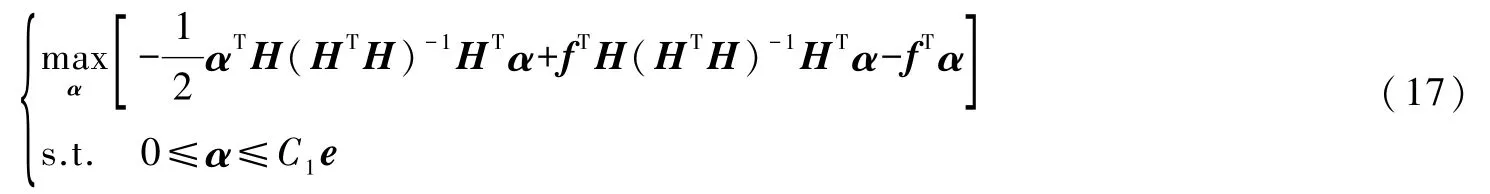
值得注意的是，由于矩阵HTH为半正定矩阵，为克服其奇异，需引入正则项σI，故式（16）可改写为

式中：I为单位矩阵；σ为正数。

同理，对式（6）引入非负拉格朗日乘子向量β＝（β1，β2，…，βm）和γ＝（γ1，γ2，…，γm），并结合KTT条件可得式（6）的对偶优化问题

与f2（x）的解

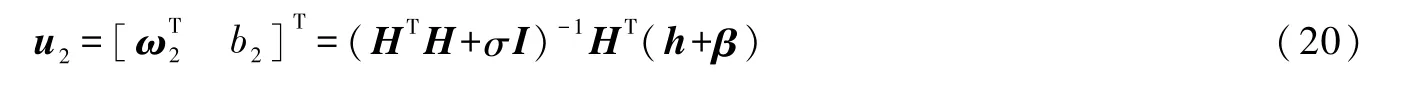
式中h＝y＋eε2。

通过求解式（17）与式（19）得到α与β的最优解，即可解得u1与u2，进而可确定式（3）所示的TSVR回归模型。

3.2 基于WOA优化的TSVR考虑到惩罚参数C1、C2，不敏感损失函数参数ε1、ε2，正则项参数σ以及RBF核宽度参数λ的选取对TSVR算法的训练精度与泛化性能影响显著，而基于群智能优化算法的参数求解是确定机器学习算法最优参数的最常用技术手段，故本文采用Mirjalili和Lewis受座头鲸独特的气泡网猎食行为启发提出的WOA算法［28］对TSVR参数优化求解。

WOA算法以一定概率P控制搜索代理选择收缩包围或螺旋上升两种机制模拟座头鲸的气泡网猎食行为。当pi＜P时，通过收缩包围机制更新搜索代理的空间位置，如式（21）所示；反之，则通过螺旋上升机制更新其空间位置，如式（22）所示。

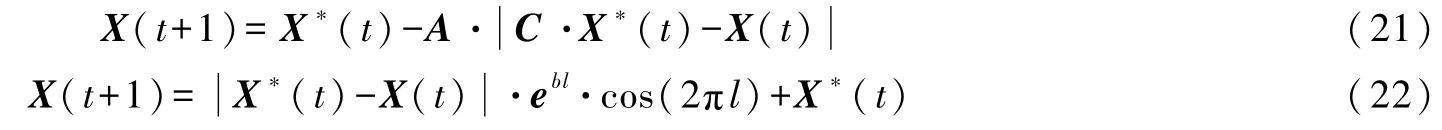
式中：X*与X分别为当前最优解与搜索代理的空间位置向量；t为当前迭代次数；A与C为系数向量，其中，A＝2a·r-a，C＝2·r，向量a随迭代次数的增加从2线性递减至0，a＝2-t/tmax，tmax为最大迭代次数，r为［0，1］区间内的随机向量；b为决定对数螺旋线形状的常数；pi与l分别为［0，1］和［-1，1］区间内的随机数。相关研究指出，当P取0.3时，WOA算法具有更优的收敛速度与训练精度［34-35］，故本文取P＝0.3。

式中：Xr为随机选择的搜索代理的空间位置向量。

基于上述WOA基本原理，TSVR参数可通过WOA迭代优化过程中搜索代理的空间位置更新加以确定，搜索代理的空间位置坐标X＝（x1，x2，…，xd）为TSVR参数的可行解，搜索空间的维度d取决于TSVR算法中待求解的参数个数，在此取d＝6。TSVR算法的最优参数即为适应度函数值最小时所对应的搜索代理的空间位置坐标，本文采用均方根误差（Root Mean Square Error，RMSE）作为适应度函数，即

式中：δi为实测变形；δ′i为训练得到的变形；n为训练样本容量。

基于式（1）所述的混凝土重力坝变形及其解释变量间的因果关系，结合WOA优化求解TSVR参数，据此可构建基于优化TSVR的混凝土重力坝变形预测模型，建模流程如图3所示，具体实现步骤如下：

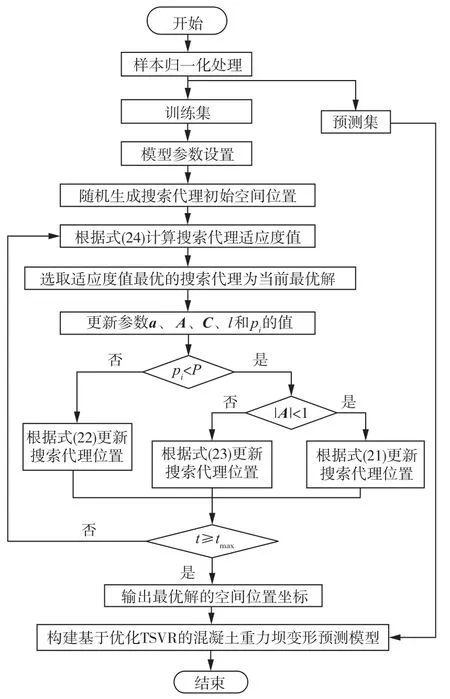
图3 基于优化TSVR的混凝土重力坝变形预测模型实现流程

步骤1：模型参数设置与样本归一化。设置WOA算法中搜索代理个数N与最大迭代次数tmax以及TSVR算法待求解参数的取值上、下界，并对解释变量做归一化处理，即

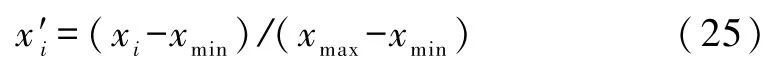
式中：xmax与xmin分别为某一解释变量的最大与最小值。

步骤2：随机生成搜索代理的初始空间位置。为保证WOA算法初始解的多样性，搜索代理的初始空间位置可随机生成为

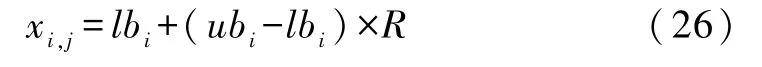
式中：xi，j为第j个搜索代理的第i维空间坐标；ub和lb分别为TSVR算法第i个待求解参数取值的上、下界；R为［0，1］区间内的随机数；i＝1，2，…，d；j＝1，2，…，N。

步骤3：根据式（24）计算各搜索代理的适应度值，并保留适应度值最小的搜索代理为当前最优解。

步骤4：更新WOA算法中a、A、C、l及pi的值。

步骤5：更新搜索代理空间位置。当pi≥P时，通过式（22）更新搜索代理空间位置；反之，当时根据式（23）更新搜索代理空间位置，当时则依据式（21）更新搜索代理空间位置。

步骤6：判断迭代是否终止。若当前迭代次数小于tmax，则重复执行步骤3至步骤5；反之，迭代终止并输出最优解的空间位置坐标，据此即可构建基于优化TSVR的混凝土重力坝变形预测模型。

4 实例分析

4.1 工程背景某混凝土重力坝位于我国西北高纬度严寒地区，该地区年内温差达60余℃，最低气温小于-30℃，多年平均气温低于5℃。如图4所示，相比于温暖地区（如四川），该地区呈现出昼夜温差与年内温差大、极端低温且低温期历时久的鲜明气候特征。

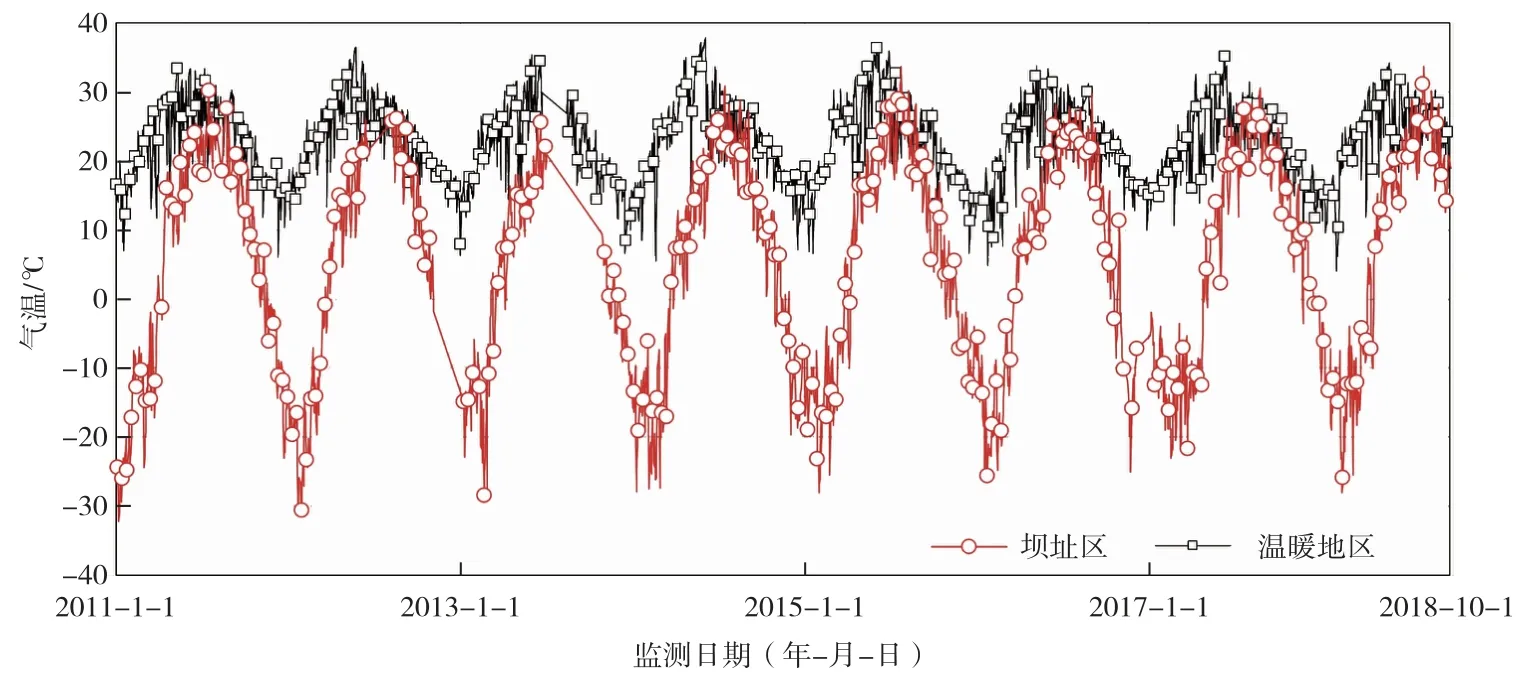
图4 坝址区气温过程线

该混凝土重力坝工程规模庞大，坝顶长1570.0 m，由87个坝段组成，主河床坝段下游立视图如图5（a）所示。位于主河床的29＃表孔溢流坝段及与其坝高相近的35＃挡水坝段的变形与温度监测仪器布置分别如图5（b）（c）所示。2016年1月1日至2018年10月1日期间库水位与29＃和35＃坝段各测点顺河向水平位移的变化过程如图6所示。

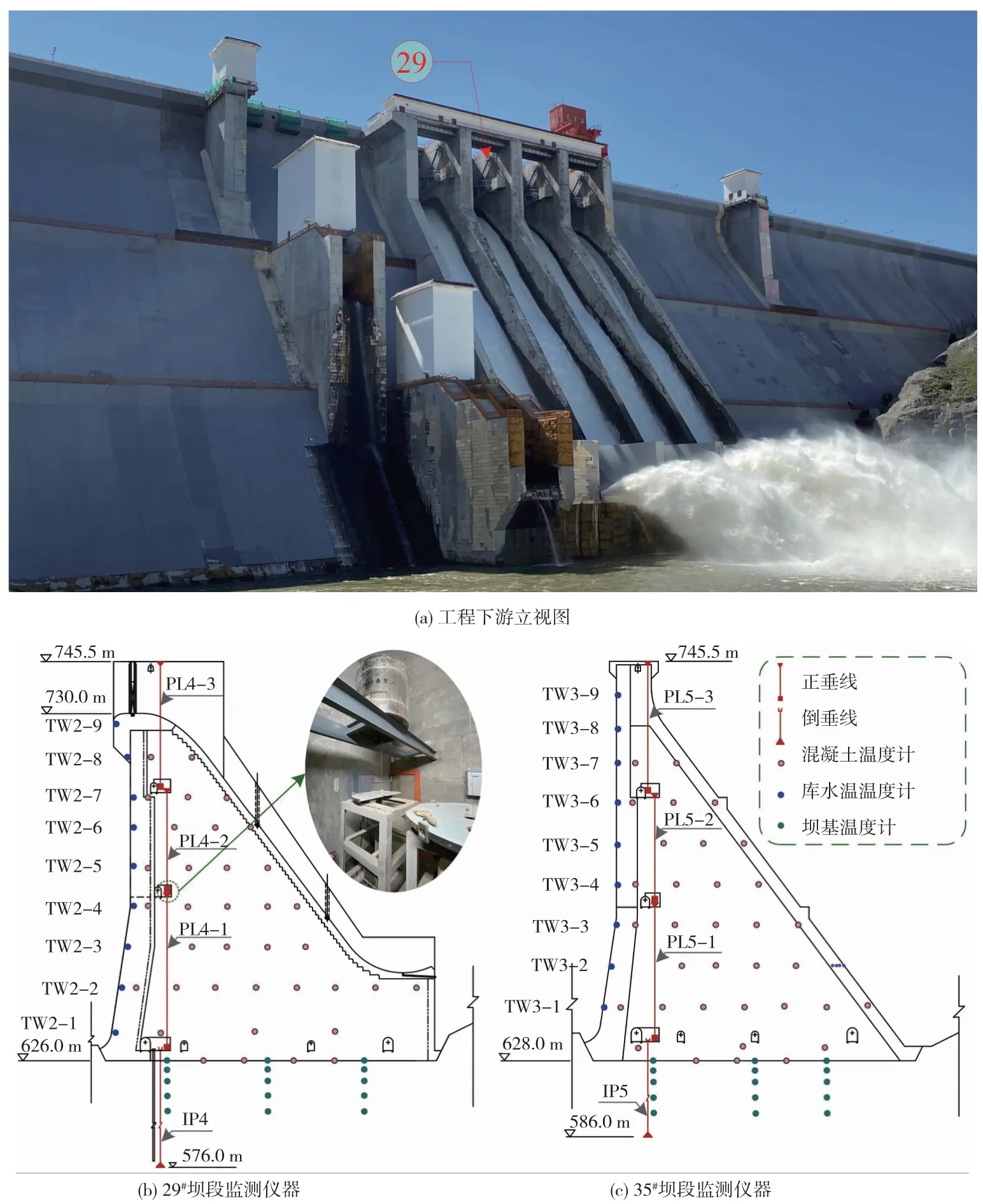
图5 主河床坝段外观与典型坝段监测仪器布置

4.2 不协调变形行为及其成因分析

4.2.1 29＃坝段坝顶不协调变形行为 由图6可知，各测点顺河向水平位移均为正值，表明大坝整体向下游方向变形。值得注意的是，29＃坝段坝顶PL4-3测点与其它正垂测点的水平位移变化行为不协调，主要表现在以下两方面：（1）除PL4-3测点水平位移外，其它正垂测点的水平位移均与库水位变化呈现出明显的正相关关系，即大坝向下游方向变形随库水位的上升而增大或随之下降而减小，而29＃坝段坝顶PL4-3测点水平位移变化规律与之相反；（2）其它正垂测点水平位移年最大值与最小值分别出现在高水位与库水位下降期，而29＃坝段坝顶PL4-3测点水平位移年极值分布与之相反，且其水平位移年变幅显著大于其它正垂测点的水平位移年变幅。综上所述，29＃坝段坝顶PL4-3测点与其它正垂测点水平位移变化规律有显著差异，表明29＃坝段坝顶的变形行为不协调。

图6 库水位与水平位移实测过程线

4.2.2 29＃坝段坝顶不协调变形行为成因剖析 针对29＃坝段坝顶的不协调变形行为，需分析其成因以甄别该坝段是否存在结构病损或运行安全隐患。为此，本节基于式（1），利用最小二乘法构建了29＃与35＃坝段PL4-3、PL4-2、PL5-3及PL5-2测点的变形行为分析模型，并分离了实测变形中所蕴含的水压、温度与时效分量，各测点变形分量的分离结果如图7所示，图中 “-”表示向上游方向变形。除PL5-2测点变形行为分析模型的决定系数R2略大于0.80外，其它测点变形行为分析模型的决定系数R2均大于0.90，表明建模精度整体良好。R2的计算方法如下

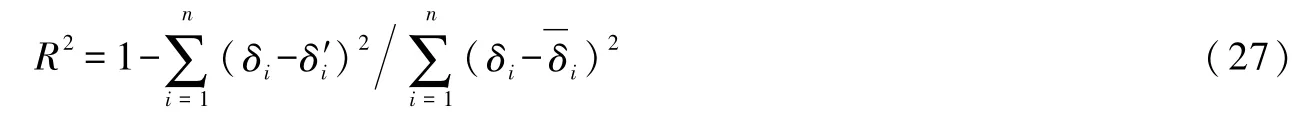
通常而言，时效分量反映大坝变形的长期趋势性变化特征，而水压与温度分量则表征大坝在环境荷载作用下的短期动态变形行为。由图7可知，分离得到的各测点水平位移的水压与温度分量的变化规律分别一致，总体上均表现为水压分量随库水位的抬升而增大，且温度分量随环境温度的升高而减小，其符合混凝土坝变形的一般规律。同时，所分离的温度分量可有效刻画环境温度短期动态波动引发的热变形细节特征，进而有效佐证了基于实测边界温度的混凝土坝变形行为分析模型的合理性及其对热变形的解译性能。相比而言，各测点水压分量变幅相差不大，虽PL5-3测点水压分量变幅稍大，但仅比变幅最小的PL4-3测点的水压分量变幅大约3 mm；然而，PL4-3测点与其它测点的温度分量变幅差异悬殊，其中，PL4-2、PL5-3与PL5-2测点的温度分量变幅相仿且较为接近各自的水压分量变幅，但PL4-3测点的温度分量变幅达约12 mm，显著大于其它测点的温度分量变幅及该测点的水压分量变幅。

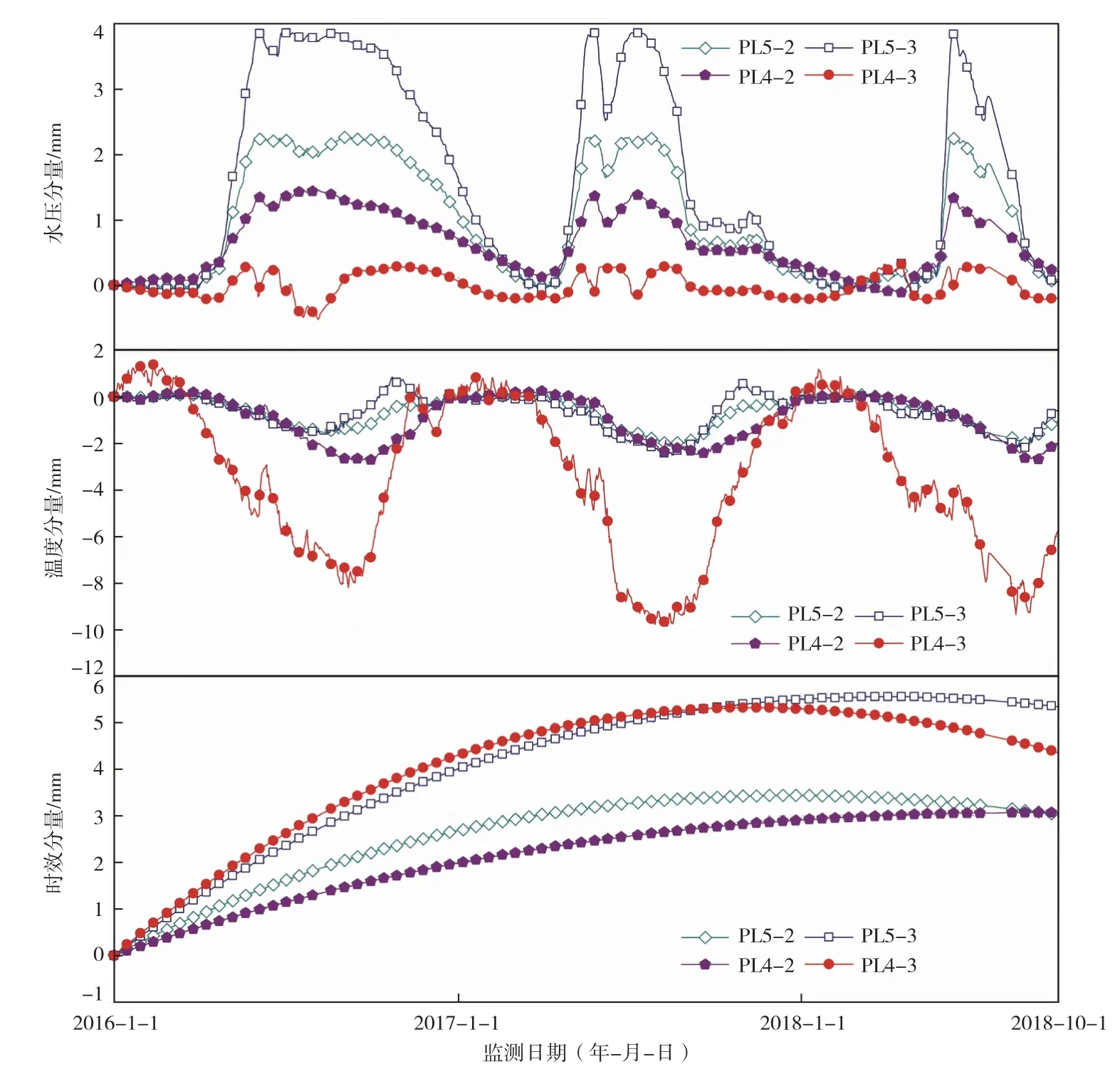
图7 水压、温度与时效分量分离结果

综上所述，29＃坝段坝顶变形行为不协调的主要原因是PL4-3测点的温度分量变幅显著较大所致。具体而言，该测点大变幅的温度分量掩盖了水压分量的变化特征，导致29＃坝段坝顶水平位移呈现出与其它测点变形行为相反的变化规律与年极值分布特征；同时，由于各测点的水压分量变幅接近，而PL4-3测点的温度分量变幅显著较大，致使29＃坝段坝顶水平位移变幅亦相对较大。结合该坝段结构型式与测点布置不难解释，29＃坝段坝顶温度分量变幅大的主要原因是PL4-3测点埋设于该表孔溢流坝段顶部中墩内，该部位混凝土厚度相对较薄致使其热变形受环境温度变化影响显著。因此，29＃坝段坝顶的不协调变形行为与该坝段结构型式有关，其客观反映了该坝段特殊结构在环境荷载作用下的运行性态变化规律。

4.3 基于TSVR的变形预测基于最小二乘法构建的模型具有良好的变形行为分析能力，但该方法的建模精度相对较低，尤其是PL5-2测点变形行为分析模型的决定系数尚不足0.90。为提升模型的拟合与预测精度，本节采用基于WOA优化的TSVR算法构建混凝土坝变形预测模型，并以PL4-3测点实测水平位移为例详细阐述建模流程。为避免TSVR参数盲目取值对模型性能的影响，首先结合WOA算法迭代求解TSVR的最优参数，相关参数设置如下：TSVR算法中惩罚参数C1、C2与不敏感损失函数参数ε1、ε2的上、下界均设置为100与1×10-4，正则项参数σ的上、下界设置为1×10-2与1×10-8，RBF核宽度参数λ的上、下界设置为10与1×10-4；WOA算法中搜索代理个数与最大迭代次数分别取N＝30和tmax＝200。取2016年1月1日至2018年6月30日期间的监测数据，并结合混凝土重力坝变形及其解释变量间的因果关系给定模型的输入与输出用以模型训练，剩余监测数据用以检验模型的预测性能。WOA算法的迭代收敛过程如图8所示。

由图8可知，经过15次迭代，适应度函数RMSE收敛于0.1253 mm，表明WOA算法具有良好的收敛速度与精度。利用WOA优化求得的TSVR最优参数，即可构建基于优化TSVR的PL4-3测点水平位移预测模型。为检验所建模型的有效性与普适性，同时利用该方法构建PL4-2、PL5-3与PL5-2测点的水平位移预测模型，并采用SR、MLR与GRU算法分别对上述测点的水平位移建模预测。各测点变形预测模型的拟合与预测结果及建模残差分别如图9与图10所示。此外，为进一步量化评估预测模型的拟合与预测精度，综合采用决定系数R2、平均绝对误差（Mean Absolute Error，MAE）、均方误差（Mean Square Error，MSE）和平均绝对百分误差（Mean Absolute Percentage Error，MAPE）分别计算了各测点预测模型拟合与预测段的统计指标，如图11所示。其中，MAE、MSE与MAPE的计算方法如下

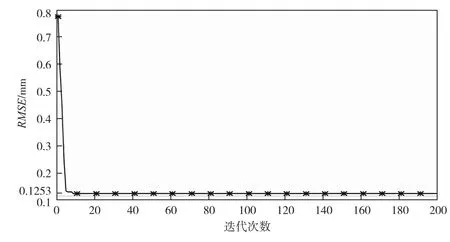
图8 WOA迭代优化过程

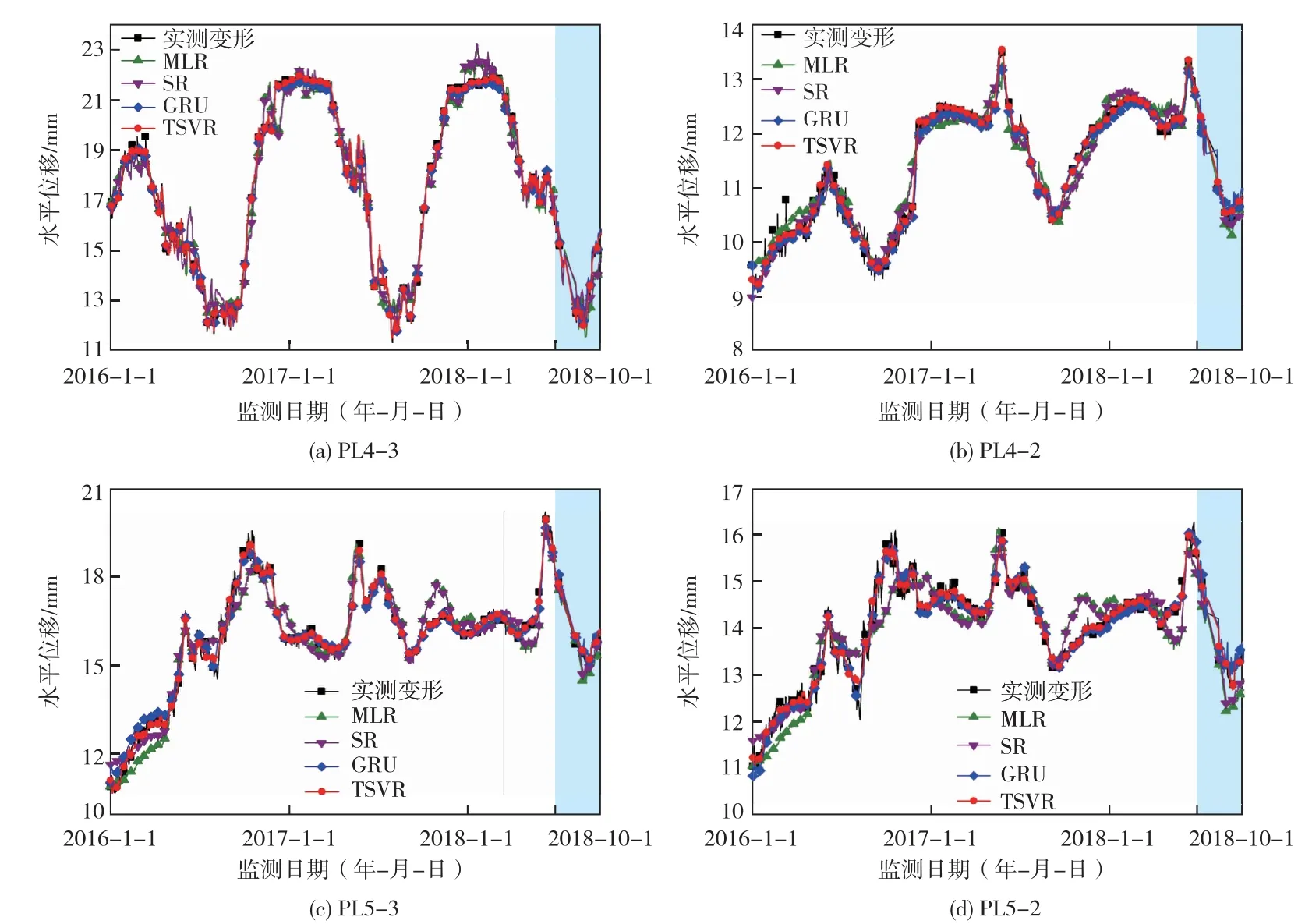
图9 各测点变形预测模型的拟合与预测结果

图10 各测点变形预测模型的建模残差

图11 建模性能评价指标

由图9可知，4种方法构建的各测点变形预测模型的拟合和预测值均与实测值的变化规律一致，且基于优化TSVR与GRU算法所建预测模型的拟合和预测值更为接近实测变形；同时，由图10可知，基于优化TSVR与GRU算法的预测模型比基于SR与MLR算法的预测模型的建模残差更小，因此，基于优化TSVR与GRU算法构建的变形预测模型具有更高的拟合与预测精度。相比基于GRU算法的预测模型，基于优化TSVR的预测模型的拟合与预测值更为接近实测变形且建模残差更小，由此可知，基于优化TSVR的预测模型更能有效地挖掘大坝变形与其解释变量间复杂的非线性函数关系，且具有更优的拟合与预测性能。同时，结合图11中的建模性能评价指标可知，相比SR、MLR与GRU三种算法构建的预测模型，基于优化TSVR算法构建的4个典型测点的变形预测模型的决定系数R2均显著接近于1，且拟合段与预测段的MAE、MSE和MAPE均相对更小，其进一步表明基于优化TSVR的变形预测模型具有出色的拟合与预测性能。此外，基于优化TSVR的预测模型拟合段与预测段的MAE、MSE和MAPE均分别接近，表明所建模型不存在过拟合或欠拟合问题，在验证利用WOA算法优化求解TSVR参数有效性的同时，进一步佐证了基于优化TSVR的混凝土坝变形预测模型的稳健性与普适性。所建模型可为高精度预测大坝变形行为提供一种新手段。

5 结论

考虑到严寒地区独特的气候特征，构建了基于实测边界温度模拟热变形的混凝土重力坝变形行为分析模型，并利用WOA优化的TSVR算法，提出了具有出色拟合与预测性能的混凝土坝变形预测模型。同时，结合所建模型剖析了严寒地区某混凝土重力坝表孔溢流坝段坝顶不协调变形行为的成因，研究结果对深入认识严寒地区混凝土坝服役性态、高精度预测大坝未来变形行为具有重要的理论价值和借鉴意义。主要结论如下：（1）严寒地区某混凝土重力坝29＃表孔溢流坝段坝顶变形行为不协调的主要成因，是该坝段坝顶中墩混凝土厚度较薄导致该部位变形行为受环境温度变化显著影响，大变幅的热变形致使该坝段坝顶测点与其它测点的变形行为存在明显差异。该不协调变形行为系结构型式的固有差异所致，不表明大坝存在结构病损等运行安全问题，其对深入认识严寒地区混凝土坝的变形行为具有重要的理论意义与工程指导价值。（2）基于实测边界温度模拟热变形的混凝土坝变形行为分析模型，可较好地解译环境温度短期动态波动引发的热变形细节特征，所建模型具有良好的大坝变形行为解释能力。同时，通过WOA算法优化求解TSVR参数，并据此提出的基于优化TSVR的混凝土坝变形预测模型，可有效地挖掘大坝变形及其解释变量间复杂的非线性函数关系，所建模型具有优异的拟合和预测性能，为高精度预测大坝变形提供了新的技术手段。