基于分形理论的黄河内蒙古段河势演变特征及其与凌汛灾害关联研究

田福昌，苑希民，何立新，王秀杰，王丽娜，岳志春

（1. 天津大学水利工程仿真与安全国家重点实验室，天津300072； 2. 天津大学建筑工程学院，天津300072；3. 河北工程大学水利水电学院，河北邯郸075000；4. 中国市政工程华北设计研究总院有限公司智慧水务分公司，天津300074）

1 研究背景

黄河内蒙古段位于黄河流域最北端，具有特殊的“几”字形河湾形态与水文气象条件，历史凌汛灾害频繁发生，并造成严重影响［1-2］。凌汛灾害与热力环境、水流动力因素、河道边界条件及人类活动等密切相关［3-7］，复杂条件变化驱动下黄河内蒙古段凌情与凌汛灾害不断呈现新的演变特征。河势作为河道边界条件之一，严重影响着凌汛灾害产生与发展，研究河势演变特征及其与凌汛灾害的关联关系，对于凌汛灾害易发河段的早期识别、预测及其灾害风险防控具有重要意义。

关于分形理论在河势演变中的应用研究，一直是国内外地理学与水利工程学领域研究的热点。Mandelbrot作为分形理论的创始人，最早于1977年将分形学引入地理水文学领域［8］，探讨了河流长度与流域面积的相关关系，随后Feder 等［9］推导了主河道分形维数计算公式。Robert［10］研究了反映河床剖面粗糙度分形特征的标度指数。Tarboton 等［11］基于分形理论建立了河流地貌演化与河网密度的联系。Nikora等［12］利用河流中心线分形维数来表征河流平面形态的内部结构特征。Nykanen等［13］尝试应用自组织临界理论诠释了河流演变过程。Ni等［14］研究了水库泄流影响下下游河道横断面分形维数的变化规律。Feng 等［15］利用分形树理论探讨了水文学领域小流域地形地貌的分形特征。Wang 等［16］分析了城市化背景下黄河流域河网多重分形特征。张矿［17］认为分形维数能够反映河流形态复杂程度。汪富泉等［18-20］探讨了河流分形结构及其形成机制，揭示了河流平面形态的演变规律。金德生等［21］研究了大江大河河床纵剖面分形特征。冯平等［22］计算了海河水系河长和河网分形维数。白玉川等［23］描述了大江大河不规则程度和弯曲度分形特征。周银军等［24］分析了河床表面分形特征及其度量方法。徐国宾等［25］研究了黄河不同河型径流量、宽深比和输沙量的非线性特征。关于分形理论在凌汛灾害中的应用研究，Xu等［26］基于分形理论研究了冰破坏强度的尺度效应。近年来田福昌等［27］综述了国内外河流（网）非线性动力系统防灾分形理论研究进展，提出流域多尺度洪灾分维动力机制、河流演变复合参数分形特征与物理机制等是分形混沌学与灾害学交叉发展的重要研究方向；之后较为系统地分析了黄河宁蒙段凌汛洪水风险分类及其分布特征，结果表明冰塞冰坝壅水漫滩以及堤防漫溃决高风险区域多位于三湖河口至头道拐河段，凌汛期堤防险段或防凌薄弱点多呈空间非连续性分布特征，反映了凌汛期上下游河势弯道孕灾环境的显著差异性［28］。罗红春等［29］基于分形理论研究了弯道冰下水流流速垂线分布规律。苑希民等［30］提出了一种基于分形理论和SVM 的高分遥感凌汛灾害信息智能识别提取方法，并应用于黄河内蒙古段三湖河口弯道凌汛期河冰的快速识别与智能分类。综合上述，分形理论在不同维度河势演变研究中得到了很好应用，而且近年来众多学者将分形理论引入到凌汛灾害机理机制研究，取得较为丰硕的研究成果；已有研究表明凌汛灾害易发河段的“弯道效应”十分明显［31-33］，河势作为凌汛灾害产生与发展最关键的影响因素之一，量化河势演变特征及其与凌汛灾害（冰塞/冰坝）的关联关系，对于凌汛灾害防御与风险管理至关重要，而河势演变分形维数已被证明能够很好地量化河势分形特征，可为此定量化研究提供新的思路和方法。

基于此，本文拟根据分形理论原理，提出横断面河相系数和水位-面积关系、纵剖面深泓点高程和平均底坡、平面弯曲形态等不同维度河势分形维数计算方法，并计算黄河内蒙古段横断面、纵剖面与平面河势的分形维数，研究不同维度河势分形特征及其与凌汛期冰塞冰坝灾害的关联关系，以量化揭示寒区河道凌汛灾害的“弯道效应”。

2 研究区域概况

黄河内蒙古段属于黄河流域上游二级阶地，穿越乌海市、包头市、鄂尔多斯市等市、县（旗、区），河段全长830 km，位于黄河流域最北端，整体呈现“几”字形大河湾，地理位置如图1所示。黄河内蒙古段河道弯曲、主槽滩地冲淤变化频繁、主流摆动不定、坡度较缓、河型较多，常出现河床高于地面的悬河。由于特殊地理地形环境影响，黄河内蒙古段水流由低纬度流向高纬度且受阴山山脉影响，冬季气温上暖下寒，封河自下而上；翌年春季气温南高北低，开河自上而下。流凌封河期，下游先封河，水流阻力加大，上段流凌易在封河处产生冰塞，壅水漫滩，严重时造成堤防决口；开河期，上游先开河、下游处于封冻状态，上游大量冰水沿程汇集流向下游，极易在弯曲、狭窄河段卡冰结坝，壅高水位，造成凌汛灾害。目前该河段已建成由上下游水库、堤防、河道整治工程（控导工程与险工险段工程）、应急分凌区等组成的较为完善的防洪防凌工程体系，总体形成了“上控-中分-下排”的防凌调度方案，上游至下游沿程建有石嘴山、巴彦高勒、三湖河口、昭君坟、头道拐等重要水文站，主要观测不同断面位置水位、流量、泥沙和水温等信息。黄河内蒙古段干流堤防长986.73 km，加上海勃湾枢纽库区堤防22.24 km（左岸17.96 km、右岸4.28 km），共有堤防长度1008.97 km，其中连续堤段主要分布在三盛公水利枢纽以下平原河道两岸，石嘴山至三盛公库区两岸堤防为不连续分布。在气候变化与人类活动耦合作用愈发凸显的情况下，黄河内蒙古段凌汛灾害不断呈现孕灾环境复杂、突发链发性强、防御困难等特征，防凌形势依然严峻［34］。

图1 黄河内蒙古段

3 研究方法与数据

根据黄河内蒙古段（石嘴山至头道拐河段）水文测验横断面河相系数及水深-面积关系、沿程纵剖面深泓点高程与河底坡度、卫星遥感影像等历史数据，采用R/S分析法计算相关时间序列的赫斯特数和分形维数，分析不同变量随时间变化的趋势、波动性及长程相关性，并基于分形定义提出横断面水深-面积分形维数计算方法。根据黄河内蒙古段历史冰塞冰坝河段形态，分析冰塞险情易发河段的弯曲特性，并基于多年卫星遥感影像提取黄河干流平面形态，采用盒维数法计算不同河段平面弯曲分形维数，探讨横断面、纵剖面与平面等不同维度河势分形特征及其与冰塞冰坝的关联关系。

3.1 时间序列分形维数R/S分析法R/S分析法是由赫斯特在1965年提出的一种时间序列统计方法［35］。假设存在时间序列ξ(t),t=1, 2, 3, …,N；对于任意正整数τ≥1，定义其均值序列：

用X(t)表示累积离差：

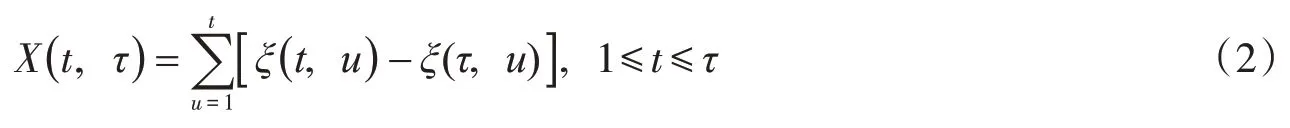
极差R与标准差S定义为：

赫斯特发现存在经验标度关系：

式中：H为赫斯特数；e为常数。

分式布朗运动随机分布函数BH( )t，布朗运动时间标度bτ，高为ba的总盒子数：

式中：T为记录轨迹的时间；D为多时间尺度自相似分形维数，D=2-H，表征时间序列变化波动性或易变性。

分布式布朗运动的长程相关性与持久性时间相关函数c(t)：

令BH( 0 )=0，则：

由以上各式可以看出，H值一般介于0和1之间，以H=0.5为分界，不同区间表现出不同的性质：

当H=0.5时，D=1.5，c（t）=0，说明时间序列属于独立随机的布朗运动；

当H>0.5 时，D<1.5，c（t）>0，说明时间序列存在一定长程相关性和持久性，过去与未来变化趋势一致，变化增量呈现正相关关系；

当H<0.5 时，D>1.5，c（t）<0，说明时间序列具有反持久性，过去与未来变化趋势相反，变化增量呈现负相关关系。

为了判定时间序列变化的长期记忆性，建立统计量Vτ：

通过Vτ与lnτ关系曲线可以判定时间序列变化的长期记忆性：若该曲线为平坦直线变化，则时间序列为独立随机过程，不存在记忆性；若该曲线为向上倾斜变化，曲线拐点对应τ值即为记忆周期长度；若Vτ达到峰值后开始变得衰减平坦，说明长程记忆过程开始耗散。

3.2 横断面水深-面积分形维数计算方法1986年，Mandelbrot B.B.给出了简单直观的分形定义：设

集合A×En，如果A的局部以某种方式与整体相似，则称A为分形集。分形分布满足以下条件［36］：

对上式两端取自然对数得：

式中：s为欧式长度；y为度量尺码；D为分形维数；a为比例常数。将lns和lny点绘于双对数坐标，拟合直线斜率为-D，则分形维数等于D。

本文中河道横断面水深-面积分形维数是指不同水深对应于断面过流面积的维数，水深与过流面积之间为正相关关系且存在一定的自相似性，记为：

两端取对数得：

式中：HH为水深，m；S为断面过流面积，m2；D为横断面水位-面积变化的多尺度自相似分形维数，主要与断面形态有关；k为比例常数。

3.3 河道平面弯曲分形维数计算方法采用盒维数法计算河道平面弯曲自相似分形维数［27］：设A是n维欧式空间的子集，δ为闭球半径，对每一个δ>0，用Nδ（A）表示覆盖A的半径为δ的闭球最少个数，记lnNδ(A) =-Dlnδ+C，若存在，则称此极限为集A的盒维数D，Nδ（A）≈cδ-D，即为覆盖A的闭球数幂律，其中C=lnc。基于GIS平台的不同尺度盒子覆盖情况，如图2所示。

图2 基于GIS平台不同尺度盒子覆盖示意图

4 研究结果与讨论

4.1 横断面河势分形特征

4.1.1 河相系数 根据不同水文测验断面历年河相系数，采用R/S分析法计算河相系数随时间变化的赫斯特数H、分形维数D、长程相关性参数c（t）和记忆周期τ，如表1和图3所示。河相系数分形维数的物理意义是表征平滩流量下横断面宽深比河相易变波动性，不同断面河相系数变化具有多尺度自相似分形特征；不同测验断面统计参数H>0.5且c（t）>0，说明河相系数变化具有正向长程相关性，变化趋势相关程度由大至小分别为三湖河口站、头道拐站、石嘴山站和巴彦高勒站，对应最长记忆周期分别为23 a、23 a、23 a和6 a，中间出现若干短时记忆耗散现象；河相系数分形维数由大至小排序依次为巴彦高勒站、石嘴山站、头道拐站和三湖河口站，说明巴彦高勒站断面河相系数的易变波动性最大，石嘴山站次之，三湖河口站最小。

图3 不同水文测验断面河相系数赫斯特数与长程记忆周期图

表1 不同测验断面河相系数R/S分析结果统计

4.1.2 水深-面积关系 根据不同测站不同年份实测断面数据，计算不同水深对应断面过流面积，绘制lnHH与lnS双对数散点图，如图4 所示，不同年份不同测验断面水深-面积分形维数，如表2 所示。横断面水深-面积分形维数的物理意义是表征不同水深对应河槽宽度增量的波动性，不同断面水深-面积关系变化具有多尺度自相似分形特征；同一测站水深-面积分形维数年际变化较大，不同断面水深-面积分形维数的多年均值由大至小排序依次为三湖河口站、巴彦高勒站、头道拐站和石嘴山站，说明三湖河口站断面水深-面积关系易变程度最高，不同水深对应河宽的变化波动性最大，巴彦高勒站和头道拐站断面次之，石嘴山站断面水深-面积关系最为稳定。

表2 不同年份不同测验断面水深-面积万倍分形维数统计表

图4 不同测站断面水深-面积分形维数统计图（以2011年为例）

4.2 纵剖面河势分形特征

4.2.1 深泓点高程 根据不同水文测验断面历年深泓点高程，采用R/S分析法计算不同断面深泓点高程变化的赫斯特数与长程记忆周期，如表3和图5所示。深泓点高程分形维数的物理意义是表征主槽深泓纵向升降的易变波动性，不同断面深泓点高程变化具有多尺度自相似分形特征；不同断面H>0.5且c（t）>0，说明深泓点高程变化具有正向长程相关性，相关程度由大至小分别为三湖河口站、头道拐站、巴彦高勒站和石嘴山站，对应最长记忆周期分别为23 a、23 a、13 a 和23 a，中间出现若干短时记忆耗散现象；不同断面深泓点高程分形维数由大至小依次为石嘴山站、巴彦高勒站、头道拐站和三湖河口站，说明石嘴山站断面深泓点高程的易变波动性最大，巴彦高勒站次之，三湖河口站断面深泓点高程的易变波动性最小。

图5 不同水文测验断面深泓点高程赫斯特数与长程记忆周期图

表3 不同水文测验断面深泓点高程R/S分析结果统计

4.2.2 河段平均底坡 根据不同河段多年平均底坡，采用R/S分析法计算不同河段平均底坡随时间变化的赫斯特数H、分形维数D、长程相关性参数c（t）和记忆周期τ，如表4 和图6 所示。河段平均底坡分形维数的物理意义是表征河段坡度的易变波动性，不同河段平均底坡变化具有多尺度自相似分形特征；不同河段统计参数H>0.5且c（t）>0，说明河段平均底坡变化具有正向长程相关性，相关程度由大至小分别为巴彦高勒-三湖河口河段（巴-三河段）、三湖河口-头道拐河段（三-头河段）和石嘴山-巴彦高勒河段（石-巴河段），对应最长记忆周期分别为>20 a、>20 a 和12 a；不同河段平均底坡分形维数由大至小排序依次为石-巴河段、三-头河段和巴-三河段，说明石-巴河段平均底坡的易变波动性最大，三-头河段次之，巴-三河段平均底坡的易变波动性最小。

图6 不同河段平均底坡赫斯特数与长程记忆周期统计图

表4 不同河段平均底坡R/S分析结果统计

4.3 平面河势分形特征

4.3.1 历史冰塞冰坝典型河段 根据《黄河冰情》记载，历史冰塞冰坝典型河段的平面形态，如表5所示，可知冰塞冰坝发生河段具有弯曲度大、浅滩和束窄等特点，弯道是凌汛期冰塞冰坝险情发生的关键位置，比如五犋牛夭子、胡成万滩、西付家圪堵等河段，均是弯曲度较大的典型河湾，弯道特征明显。上游流凌易在弯曲河段凸岸积聚形成初始冰盖，并逐渐演化成覆盖全断面的加厚冰盖，在高密度流凌条件下，弯道极易发生冰塞冰坝，其特殊河势是冰塞冰坝形成致灾的主要驱动因素。

表5 历史冰塞冰坝典型河段平面形态

4.3.2 不同河段弯曲分形特征 根据黄河内蒙古段1986 年、1989 年、1994 年、1997 年、2001 年、2007 年、2011 年和2018 年等不同年份凌汛期之前的卫星遥感影像，基于GIS 平台提取不同年份河道主槽中心线，采用盒维数法，计算不同河段不同盒子尺度对应的盒子数量，绘制lnNδ（A）与lnδ双对数散点图，并采用最小二乘法回归拟合，如图7所示。不同河段不同年份主槽弯曲分形维数，如表6所示。

由图7 和表6 分析可知：（1）河道主槽弯曲分形维数的物理意义是表征河流平面形态的弯曲性及河湾发育程度［22］，即河段蜿蜒性和不规则性，其与弯曲率并不相同，弯曲率一般表示长距离河流的整体弯曲程度，掩盖了小尺度河湾发育细节及弯道蜿蜒性［23］；（2）河道平面形态变化具有多尺度自相似分形特征，主槽弯曲分形维数多年均值由大至小排序依次为昭君坟-头道拐河段（昭-头河段）、巴彦高勒-三湖河口河段、三湖河口-昭君坟河段（三-昭河段）、石嘴山-巴彦高勒河段，说明昭君坟-头道拐弯曲型河段的河湾发育程度最高，巴彦高勒-三湖河口分汊型河段次之，石嘴山-巴彦高勒河段最小；（3）不同河段主槽弯曲分形维数年际变化较大，1986—2018年间，石嘴山至头道拐不同河段万倍弯曲分形维数的变化区间分别为［9944，10020］、［9996，10036］、［9960，10067］、［9998，10081］，说明三湖河口-昭君坟河段和昭君坟-头道拐河段河湾发育程度变化更大，一定程度反映了该河段受水沙冲淤影响，主槽摆动大、弯道较多；（4）表6 中河流主槽中心线分形维数D存在个别小于1的情况，经筛选典型局部河段对比分析，发现分形维数D<1的河段一般具有以下特点：相对于河道中心线直线长度而言，河湾弧度比较大；相当河湾尺度下，河道中心线较光滑，河势渐变较慢；正交直角坐标系下，河道走向具有蜿蜒迂回特点，即存在同一横坐标（x）对应多个纵坐标值（y）且同一纵坐标（y）对应多个横坐标值（x）。

图7 不同河段ln Nδ（A）与lnδ双对数散点图（以2018年为例）

表6 不同河段不同年份弯曲形态分形维数统计表

4.4 多维河势分形特征与凌汛期冰塞冰坝灾害的关联关系根据黄河石嘴山至头道拐段横断面河相系数与水深-面积关系、纵剖面深泓点高程与河段平均底坡、平面主槽弯曲形态等不同维度河势的多尺度自相似分形特征，建立其与历史冰塞冰坝（严重性冰塞）发生频次之间的关联关系，如表7所示。

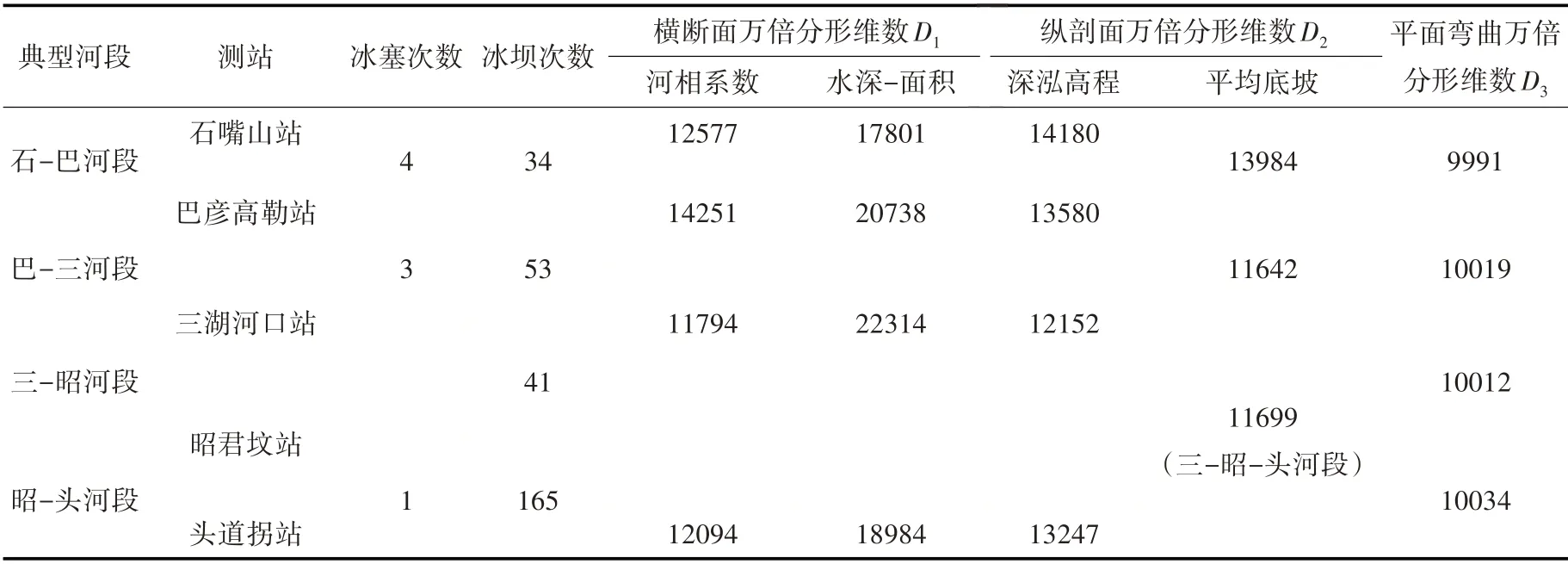
表7 黄河石嘴山至头道拐段不同维度河势分形维数与冰塞冰坝发生频次的关联关系

根据表7统计结果，建立不同河段历史冰坝（严重性冰塞）发生频次与平面主槽弯曲分形维数的关联关系，并以上下游水文测验断面河相系数、水深-面积关系、深泓高程及河段底坡分形维数的平均值作为对应河段的横断面与纵剖面分形维数，绘制横断面、纵剖面与平面等不同维度河势分形维数与冰坝发生频次的关联曲线，如图8 所示。结果表明：（1）河道多维河势分形与冰塞冰坝灾害存在一定的关联特性，其中冰坝发生频次与河道主槽弯曲分形维数呈正相关指数型关系，说明冰坝易发河段的平面形态蜿蜒曲折、河湾发育程度高、主河槽偏移摆动复杂不规则，河流弯道对凌汛期冰凌下潜、冰塞冰坝形成致灾具有正向驱动作用，论证了河道多维河势分形具有一定的实用性；（2）冰坝发生频次与河相系数、深泓高程及河段底坡分形维数呈负相关关系，说明河相系数、深泓高程和平均底坡分形维数越大，即三类因素易变波动性越大，冰坝发生概率越低，一定程度反映了河型及河槽稳定性与冰坝灾害的关联关系，比如分汊型河道（巴-三河段）河相易变但河相系数仍较小、平均底坡偏大，与三-昭-头河段相比，该河段具有窄深、坡度大等特点，因未能突破河型转化，并不构成加剧冰坝灾害形成的边界条件；（3）冰坝发生频次与横断面水深-面积分形维数正相关，说明在水沙冲淤与河床整体抬高影响下，不同水深对应断面面积或过流能力变化越大，河段宽浅化程度越高，凌汛洪水漫滩几率越大，越容易造成冰坝灾害。（4）凌汛灾害的产生与发展不仅与河道几何特征有关，同时还受气候变化、水流动力因素和人类活动（水库调度、分凌区应急调控等）多种因素影响，不同因素之间存在着密切关联关系，比如河流弯道处横断面流速分布不均，水流冲刷凹岸，而凸岸易在气温骤降和低流速耦合作用下首先结冰形成冰盖，逐渐向凹岸延伸，凌汛期弯道主槽处易出现冰凌下潜、产生冰塞或冰坝，因此凌汛灾害预测预报和风险管理需要综合考虑以上因素的耦合效应。

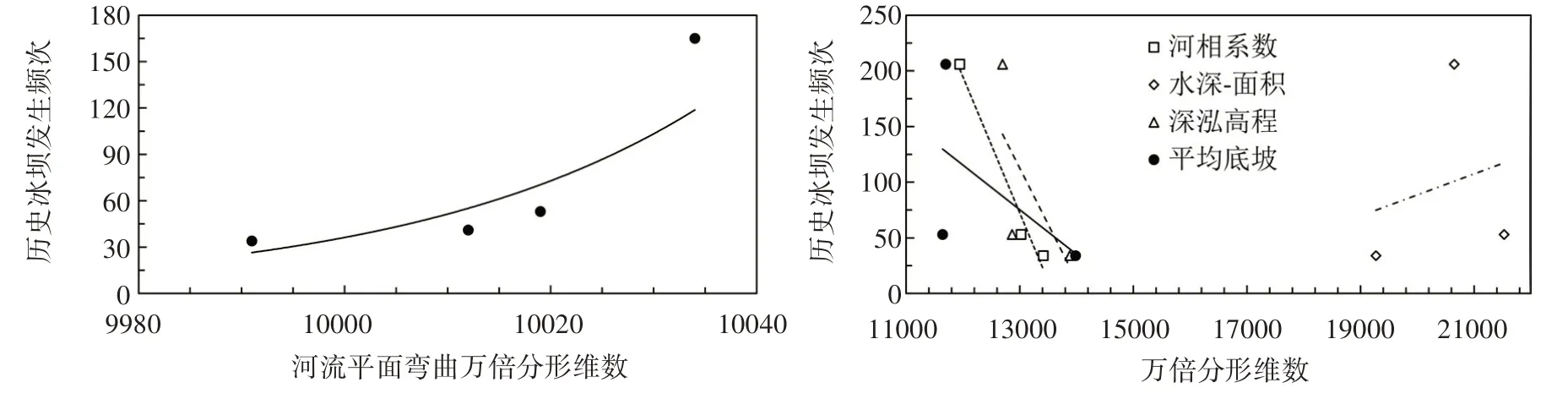
图8 不同维度河势分形维数与冰坝发生频次的关联曲线

5 研究结论

本文针对河势演变驱动下凌汛期冰塞冰坝灾害易发河段诊断及预测难题，基于分形理论，提出了河道横断面、纵剖面与平面不同维度河势分形维数计算方法，明确了各类分形维数物理机制，并研究了黄河内蒙古段不同维度河势分形演变特征及其与凌汛期冰塞冰坝灾害的关联关系，主要结论如下：

（1）河道横断面、纵剖面与平面不同维度河势均具有多尺度自相似分形特征，且具有多年记忆周期的长程相关性，冰坝发生频次与河道主槽弯曲分形维数呈正相关指数型函数关系，定量化论证了凌汛灾害诱发的河势“弯道效应”，进一步丰富了凌汛灾害防治的基础理论。

（2）河型及河槽稳定性与凌汛期冰塞冰坝灾害的发生发展存在密切关联性，冰坝灾害更易发生于主槽偏移摆动大、蜿蜒曲折、河湾发育程度高的宽浅型弯曲河道，可为凌汛期冰塞冰坝易发河段预测、防凌风险管理及灾害防御提供科学依据。

（3）本文采用分形维数量化了河势演变对凌汛期冰塞冰坝灾害发生的影响程度，论证了河道多维河势分形具有一定的实用性，未来可在此基础上，从以下几方面作进一步深入研究，比如河道横断面-纵剖面-平面多维河势耦合致灾的综合分形维数计算方法及阈值、凌汛期冰塞冰坝灾害易发弯曲河段的河势分形预测方法、凌汛期冰塞冰坝灾害发生河段的时空演变规律及其河势分形驱动机制等。