北京三百年降水序列的成分分析及其随机模拟

门宝辉，张 腾

（华北电力大学 水利与水电工程学院，北京 102206）

1 研究背景

全球气候变暖和高频人类活动加速了全球及区域尺度的水文循环过程，并导致降水量时空变化及其区域差异的不确定性增大［1-3］，而降水量时空分配不均匀除了直接体现在极端天气现象外，还对农业生产、城市洪涝、经济社会发展等多个方面产生重要影响［4-5］。

北京地区属温带季风气候，常年干旱少雨，水资源人均占有量低于300 m3，是我国严重水资源短缺的地区之一。全球温室效应和人口快速增长等问题加剧了该地区绿水资源匮乏问题，水资源已成为掣肘北京地区经济高质量发展和社会生态文明环境建设的关键因素，因此明确该区域降水量的未来发展态势具有深远意义。现阶段我国学者对包含北京在内的多个地区的降水序列变化特征等方面开展了许多研究。

李鹏程等［6］采用M-K检验法和小波变换对北京、天津地区1958—2008年降水序列变化特征及其与汛期降水周期关联进行分析，结果表明研究时域内北京、天津地区的年降水量与汛期降水量均呈现出减少趋势；宋晓猛等［7］分析了北京地区1980—2012年降水历时和降水等级的时空变化特征；尤焕苓等［8］对1981—2010年间北京地区20个常规气象观测站日降水数据进行统计计算，发现从1980年代以来北京地区极端类型降水量呈现出减少趋势；朱龙腾等［9］借助经验模态分解北京地区1951—2009年共59年降水序列，分解结果表明该地区降水量在短期内呈波动性减少趋势；鲁向晖等［10］采用累积距平法和Morlet小波变换等方法对赣江流域1966—2015年不同时间尺度下的降水时空分布特征进行分析，结果表明该流域在年尺度上汛期降水量缓慢增加，在其他时间尺度下呈不显著减少势态；徐东坡等［11］对全国1956—2018年降水序列进行Pettitt检验和小波分析，发现全国降水量呈现非显著性增长趋势，并且降水量增加趋势从西北向东南减弱。

以上研究工作剖析了北京及全国各地降水序列在不同时空尺度下的变化规律和演变趋势，具有良好的借鉴经验，但其降水数据多截止在2015年以前并且序列长度局限在50～70 a左右，其对气候变化规律研究和未来降水演变趋势不具有较强说服力。鉴此，本文研究过程如图1所示，以北京地区1724—2019年近三百年超长降水序列深入研究该地区降水变化特征和未来演变趋势，首先使用BS-Pettitt耦合模型［12］对长降水序列进行多突变点检测，然后采用极点对称模态分解算法［13］分析多时间尺度周期性以及趋势性变化规律，并选取多段代表性短降水时序进行对比分析；最后基于随机森林算法［14］构建不同长度时序下的北京地区年降水序列随机模拟模型。在降水序列组成成分分析的基础上引入随机模拟，增强研究完整性，有助于更好地研究水文时序变化情况、对比分析揭示长时间尺度序列演变规律，以期为该区域水资源系统规划设计和提高城市适应气候变化能力提供支撑。

图1 技术路线

2 方法与数据

2.1 BS-Pettitt突变检验法Pettitt检验法是由Pettitt［15］新发展的一种非参数检测法，其在有效诊断水文时序突变情况的同时，还可检验突变是否具备数学统计意义上的显著性，拟定统计量Ut，N：

式中：xt，xi为序列中的随机变量；N为序列总长度；Ut，N为新序列，由逐次统计序列中前样本数值大于后样本数值构成。若有t时刻，满足：

式中：kt，N为最大统计量；p为显著性检验指标。即可判定该点为此序列的突变点，并且其在数学统计意义上表现显著［16］。Pettitt检验在单突变点检测方面具备高效率和高精准度，但其用于多突变点检测境况时表现欠佳。因此利用二元分割法（Binary Segmentation，BS）的迭代功能，通过将水文序列分段进行Pettitt检验达到多突变点识别的目的，即构建BS-Pettitt耦合模型［12］。耦合模型具体步骤如下：

（1）设水文序列Xt（t＝1，2，…，N），采用Pettitt法对序列X［t1∶t2］（t1＝1，t2＝296）进行突变检测，并将该突变点记为k，并进行下一步，否则认为该序列无突变点。

（2）以上一步突变点k为分段点，将水文序列分成左右两部分分别重新进行Pettitt突变检测。将左半段中突变点位置记为kl，并重复检测，直到无突变点检出，记录末次分段序列t2，令kup＝t2。

（3）与（2）相似，将右半段中突变点位置记为kr，并重复检测，直到无突变点检出，记录末次分段序列t1，令kdown＝t1-1。

（4）若kup＝kdown，表明原始水文序列只有一个突变点k，否则，重新构建序列X［t1∶t2］（t1＝kup＋1，t2＝kdown），并重复（1）—（3），直到检测出水文序列全部突变点，即突变点集合Mi（i＝1，2，…，m）。

（5）将突变点集合排序后，添加1和N重新构建序列Sj（j＝1，2，…，m＋2），并依次对X［t1∶t2］（t1＝Sj，t2＝kdown）进行Pettitt突变检测，获得新的突变点集合，并重复检测，直到突变点数目恒定时，此刻的突变点集合即为多突变点最终检测结果。

2.2 去趋势预置白算法去趋势预置白算法（Trend-free Pre-whiting，TFPW）是2002年Yue等［17］提出的一种预处理技术，该方法能高效剔除序列分析时的自相关性干扰，目前已在多领域得到广泛使用［18-20］。本次研究中，TFPW 主要用于多点突变检验之前，借助剔除趋势和预置白化两部分充分削减原始序列自相关性对多突变点检测的干扰。具体步骤如下：

（1）计算水文序列为Xt（t＝1，2，…，N）的线性趋势β，则有：

（2）去除水文序列趋势成分后形成新序列Yt：

（3）计算新序列Yt的一阶自相关系数r，并对自相关系数进行显著性检验（显著性水平取0.1），如果通过显著性检验，则直接进行BS-Pettitt突变检验，若未通过，进行第（4）步的预处理。

（4）去除序列自相关项形成新序列Y′t；重新补加趋势成分形成不受自相关性干扰的新序列Y″t：

2.3 极点对称模态分解算法自1998年由Huang等［21］首次明确提出经验模态分解（Empirical Mode Decomposition，EMD），其改进算法例如集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）［22］、局部均值分解（Local Mean Decomposition，LMD）［23］、极点对称模态分解（Extreme-point Symmetric Mode Decomposition，ESMD）等在信号诊断［24］、时序分析［25］等方面均得到广泛使用。

ESMD算法是王金良等［13］基于EMD算法的新发展，其实质是以内部极点对称插值法取代EMD算法外包络线的三次样条插值法对原始研究序列进行插值处理，随后优化最末残余分量为 “最小二乘”意义下的最优 “自适应性全局平均线”，并凭此提供分解过程中的最优筛查次数，该算法在高效抑制EMD处理过程中 “模态混叠”等现象时表现良好。ESMD算法分解过程如下：

（1）标识研究序列X所有极值点，记为Ei（i＝1，2，3，…，n）。

（2）使用直线连接紧邻极值点，标记其线段中点为Zi（i＝1，2，3，…，n-1）。

（3）采用线性插值法延展序列首尾中点Z0、Zn。

（4）利用上述步骤中产生的n＋1个中点构建m条内插曲线Li（i＝1，2，3，…，m）（m≥1），并计算上述曲线的均值曲线：

（5）对X-L*新序列循环上述（2）—（4）步，截至符合以下任一条件：（a）均值曲线（ε为允许误差）；（b）迭代循环次数达到设定的允许上限值F。此时成功分解第一个本征模函数（Intrinsic Mode Function，IMF）分量M1。

（6）对X-M1新序列循环上述（2）—（5）步，依序分解得到Mi（i＝1，2，3，…，N），直至残余分量R满足其为单调序列或小于等于设定的剩余极值点数，此时通过分解得到了所有IMF分量以及残差分量。

（7）让筛选次数最大值限定在有效区间［Fmin，Fmax］内取值，之后重复以上所有过程。然后计算不同筛选次数最大值下对应的X-R序列方差σ2和方差比率σ/σ0（σ0为原始信号序列的标准差），找到方差比率最小时的筛选最大值F0。更改迭代次数允许最大值为F0，重复上述全部步骤，便可分解得到残差分量，亦是 “自适应性全局平均线”。

至此经由ESMD算法分解获得全部IMF分量以及残差分量，故原始序列可表示为：

2.4 随机森林算法Breiman基于Bagging算法改进回归树模型，创新地提出了随机森林算法［14］，该算法主要由子训练样本集和子回归模型（决策树）组成，其通过Bootstrap重抽样从原样本集中有放回地抽取多个样本组成样本容量与原样本集合一致的子训练样本集，并对每个子训练样本集构建子回归模型，即组成随机森林模型，综合所有子回归模型的子模拟结果得到最终模拟结果。该算法在大量的理论和实例中均表现出较高模拟精准度，目前已得到广泛应用［26-28］，模型计算流程见图2。

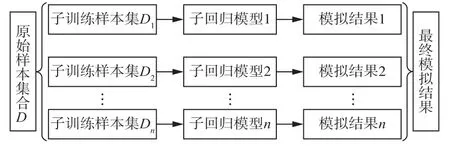
图2 随机森林模型计算流程图

在随机森林模型构建后，选定均方根误差RRMSE、平均相对误差绝对值MMRE和决定系数R2三个指标来评估模型的模拟精度，当前两者越小、后者越大时模型模拟精度越好。各指标计算公式分别为：

式中：xi为模型拟合值，mm；yi为年降水实测值，mm；ˉx为模型拟合系列值的均值，mm；ˉy为年降水实测系列值的均值，mm。

2.5 数据资料本次研究采用的数据资料是北京地区长时序面降水序列，序列长度为296年（1724—2019）（见图3），前250年（1724—1973）数据来自1970年代我国气象学者依据古籍 《晴雨录》记载数据并关联有仪器观测以来的北京气象站实测降水数据后推算延伸并整编的 《北京250年降水（1724—1973）》①中央气象局研究所.北京250年降水（1724—1973）.1975.，故认为此汇编数据具有一致性，另外从北京气象局获取北京气象站后续年份降水数据，依托北京气象站得到296年北京地区1724—2019年长降水序列数据，本研究主要集中于降水序列成分分析和随机模拟，旨在探明降水波动变化规律，而非精确量值变化，故该时序数据能够满足本次研究的需要，具有一定的空间一致性和可靠性。

图3 北京地区1724—2019年降水序列

3 降水序列组成成分分析

3.1 突变检验首先采用TFPW 检验北京地区296年降水序列是否存在自相关并进行预处理，随后将序列代入BS-Pettitt模型进行突变检验，检验结果初步表明北京地区296年降水序列存在7个突变点，突变点发生的年份分别是1742年、1770年、1813年、1871年、1893年、1947年和1999年。各时段内各突变点的Pettitt统计量Ut，N变化过程如图4（a）—（g）所示，根据突变检验的结果得到北京地区296年降水量序列的均值变化过程（见图4（h）），可以看出降水序列分段均值变化与降水序列变化情况匹配良好，能较为完整地体现出降水序列变化趋势，较为充分表明BS-Pettitt耦合模型具有较高准确性，并且结果与以往研究结论大致相同［29］。

图4 多点突变检验结果

3.2 周期项与趋势项分析采用ESMD算法对北京地区296年降水序列进行分析，分解得到7个IMF分量及1个残差分量，IMF分量分解结果如图5所示，从图中可以发现，所有IMF分量的振荡变化均线都在零值附近，其局部变化也基本对称，并且各分量的波动都存在一定的周期性。通过初步观察分量间幅值、频率的相对变化，可以发现随着分解尺度的增大，其振幅随之减小，而波长逐步增长。残差分量没有表现出明显的周期变化规律，但由于研究序列长度有限，故不排除其属于更长周期变化的组成成分的可能性。原序列残差分量可以表征北京地区年降水序列在整个研究时域上呈现 “上升—平稳—下降”的变化趋势。

图5 ESMD算法IMF分量结果

3.3 结果分析与讨论水文时序突变即意味着时序某点前后统计规律发生显著变化，能否准确并全面诊断水文时序突变点与水文序列样本容量、突变点数目、突变位置、样本及总体分布等因素息息相关，针对北京地区降水序列突变点检验研究数据多局限于50～70 a的样本容量小的现状，依据BSPettitt模型在多点突变检验过程中选取含有显著突变点的连续短时序降水时段1724—1769年、1966—2019年、1776—2000年、1813—2000年、1871—2000年、1896—2000年，并结合研究区现有文献，选取以往研究时序1951—2015年、1961—2010年、1958—2008年、1980—2012年，采用K-S（Kolmogorov-Smirnov）研判初步检验结果中各不同尺度短时序是否与296 a长时序降水具有显著性差异。设定原假设H0：两个长短时序数据所服从分布不一致（或存在显著性差异），检验结果见表1。

表1 不同时段降水时序K-S检验结果（显著性水平α＝0.05）

结合K-S检验结果与现有短时序突变点研究［6］结果发现，虽然短时序检测出的突变点如1961年、1995年，仍含在1724—2019年长时序突变检出点中且具有统计显著性，但与原时序相比仍存在不小误差，时序长短是直接影响水文时序演变规律精准度因素之一，在诊断降水序列突变点的位置及分布规律时，长时间序列更能探明更多的突变点和更长更精准的突变分布规律，更具有优势和诊断精确性。另一方面，K-S检验结果同时也对BS-Pettitt初步检验结果进行反馈研判，1724—1769年序列与原序列存在显著性差异，但仍检测出其内含显著性突变点，究其原因是因为Pettitt检验自身算法不适宜在序列首尾进行检测，存在误差，故舍去突变点1742年，分析得到原序列存在1770年、1813年、1871年、1893年、1947年和1999年6个突变点。根据K-S检验结果中显著性较高且兼具代表性的短降水时序1813—2000年、1896—2000年、1951—2015年、1961—2010年，同样对其进行ESMD分解，分解结果见图6。

由图5、图6中不同时序长度降水序列ESMD算法分解结果可以看出，各IMF分量均存在明显的周期性波动，其代表着水文序列中固有的不同时间尺度下的周期变化规律，并且随着阶数的增加，IMF分量振荡幅度减小，波长逐步增大，反映出更大时间尺度的周期变化特征。对比分析不同时序降水序列结果，依次分解出7、6、5、4、4个IMF分量和1个残差余项，结果表明长时间序列能分解出更多的IMF分量且分解结果更平稳、周期波动更单一，利用周期图法处理各IMF分量，并将各模态分量对时序整体数据变化影响以方差贡献率呈现，各降水时序的IMF分量平均周期及方差贡献率见表2。

图6 短时序ESMD分解结果

从表2中可以看出，首先，北京地区降水周期规律存在2.5～4 a、7～15 a、25～35 a、74 a左右、95～100 a的周期变化尺度，并且1724—2019年序列分解结果中涵盖其余4个时序的周期结果，从分解结果来看，更长时间序列通过ESMD算法能分解出降水序列隐含的更多更完整的周期尺度。其中，仅有1724—2019年、1813—2000年序列检测出90 a尺度周期。其次，根据方差贡献率计算结果可知，北京年降水序列在年际变化尺度以2.5～4.5 a的周期振荡变化为主，在年代际尺度上，则以16～20 a的周期振荡变化为主。1724—2019年长序列能显示北京地区三百年时间跨度上更加完整的周期变化尺度，其中以2.5～4 a的周期振荡最明显，其方差贡献率最大，年降水量以 “下降—上升—下降”的交替变化贯穿始终；年代际尺度中7～15 a和25～35 a的振荡较为明显，且呈现疏密相间的波动特征，其在1760—1790年和1835—1865年振荡波动平稳且特征相似，说明降水在此周期尺度下没有明显波动；74 a和95～100 a的周期变化尺度中，降水周期波动明显减缓，降水整体呈现出 “下降—上升—下降—上升—下降—上升—下降”的循环变化规律，很显然这是短时序无法检测出的周期尺度特征，长时序ESMD分解在降水规律分析中体现出独特的优势。时序长短不仅影响IMF分解数量和周期尺度分析，在降水序列趋势分析上同样起到关键作用。各时序残差余项结果对比分析见图7。

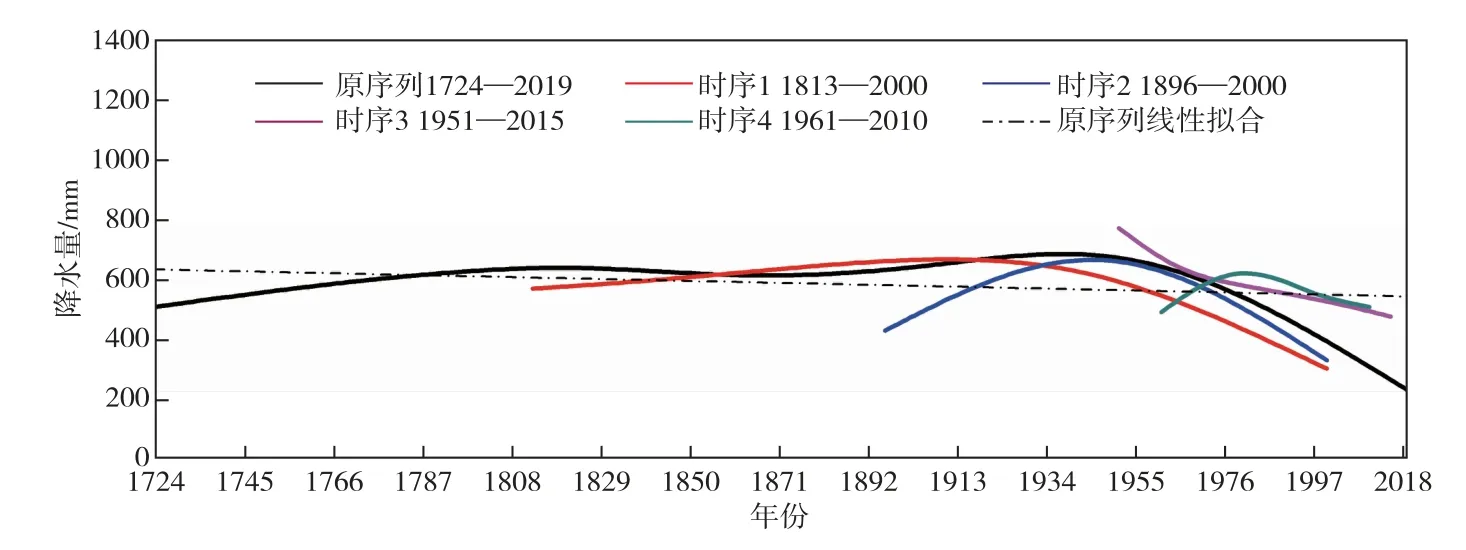
图7 各时序ESMD分解残差余项对比分析

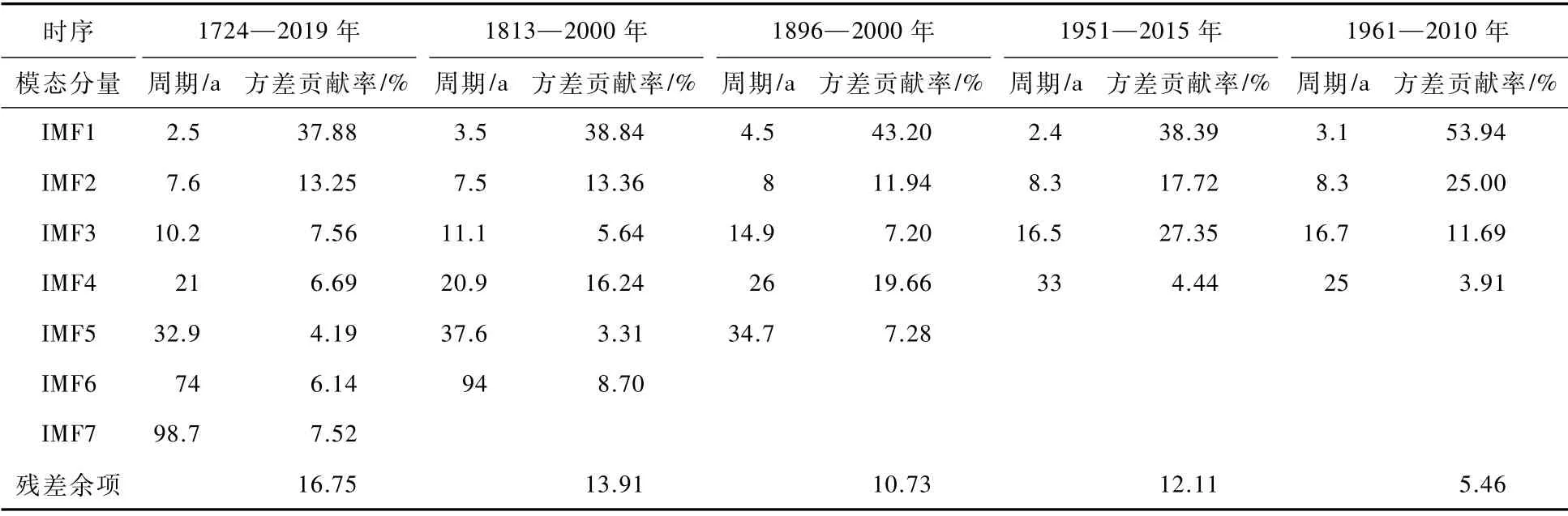
表2 各时序ESMD周期分解结果对比

由图7可见，所有序列的残差余项均在近代后期开始呈现下降趋势，但时序长短严重制约了降水序列趋势项规律分析，通过旱涝等级和树木年轮记录等代用降水资料重建的降水时序表明我国东部降水序列存在1600—1910年上升，1900年之后下降的变化趋势［30］，检测序列中仅有1724—2019年、1813—2000年序列残差分量可以表征北京地区年降水序列在整个研究时域上呈现 “上升—平稳—下降”的变化趋势，其余短时序仅能代表当前研究时域内部分趋势变化，均难以充分揭露序列演变规律，其中1961—2010年序列趋势变化结果误差明显，究其原因可能与ESMD算法本身精准度存在关联。

在北京地区降水序列成分分析中，1724—2019年长时间序列能检测出更多的突变点、更多更精准的周期尺度和更完整的趋势变化规律，表明长时间序列在降水序列成分分析体现出较强精准度和完整性，更有利于探明该地区长期降水变化规律和演变趋势，为后期降水模拟预测和防洪抗涝提供重要理论支撑。

4 降水序列随机模拟

4.1 基于随机森林的随机模拟模型构建依据前文ESMD算法对北京地区年降水序列的周期项和趋势项分析结果，初步掌握北京地区现状和未来一段时期的降水量变化趋势。本节通过随机森林算法构建北京地区年降水模拟模型。

降水模拟模型构建可分为拟合因子选取和模型参数优化两部分内容，本次模型构建依次选用时序当年四季降水量和前10年降水量共14个解释变量作为备选拟合因子，构建随机森林模型对备选拟合因子进行重要性估计。本次研究序列1724—2019年，为进一步验证长时序水文序列在时域分析中的优势，选取K-S检验中显著性水平较高且具有代表性的时序1813—2019年和1951—2019年，考虑模型训练期和验证期合适比例，分别将1724—1993年、1813—1993年、1951—1993年作为训练期样本，其余作为验证期样本，三段时序拟合因子重要性估计结果见表3。

表3 备选拟合因子重要性排序

选取表3中重要性最高的5个解释变量作为随机森林模型拟合因子。随机森林模型主要待定参数有两个：子预报决策树模型数Nt、决策树节点划分待选变量数M，前者愈大，愈能有效抑制随机模拟过程中的过拟合问题；后者愈大，愈能缩小子回归模型间的差异性。Nt通常取值应较大，M取值约等于拟合因子总数的1/3［31］。另结合数据实际情况将本次模型构建Nt取值2500，M取值3。

4.2 随机模拟结果以北京地区不同时序年降水量和相应的拟合因子系列作为模型的输入，进一步分别构建北京地区降水模拟的随机森林模型。各北京地区降水模拟模型训练期和验证期模拟分析结果见图8。

图8 不同时序降水随机模拟模型拟合结果分析

基于训练期和验证期模拟及相应年降水序列，选用决定系数R2、均方根误差RRMSE和平均相对误差绝对值MMRE三个指标评定模型精准度，指标评定结果见表4。

表4 各时序年降水序列模拟模型训练期及验证期模拟性能对比分析

由表4可知，由三个时序分别构建的北京地区降水模拟模型在训练期均表现出较高水平的模拟精度，其中1724—2019年序列误差最小，1951—2019年序列误差最大，三个随机模拟模型确定性系数R2均达0.98，平均相对误差绝对值MMRE均小于5%，除1951—2019年模型外，其余时序模型均方根误差RRMSE均小于25。验证期精度虽低于训练期，但三个随机森林模拟模型平均相对误差绝对值小于15%，确定性系数均达0.80以上，其中1724—2019年序列误差最小，1813—2019年序列在均方根误差和平均相对误差绝对值指标均优于1951—2019年序列。结合图8可知，本次构建的所有年降水随机森林模型模拟精度均较高，在训练期和验证期均表现出较高的模拟精准度。

4.3 结果讨论本次研究从定性和定量两个视角实现北京地区年降水模拟，定性为定量提供依据，定量具体化表述定性，两者结果相辅相成。在定性分析中，ESMD算法分解结果中各IMF分量表明北京地区近三百年降水序列存在2.5～4年、7～15年、25～35年、74年左右、95～100年的周期尺度变化规律，其中以2.5～4年的周期年际变化尺度为主；残差余项表明降水序列存在 “上升—平稳—下降”的整体变化趋势，且近年来下降势态加剧。

基于随机森林模型构建的北京地区年降水随机模拟模型高精度地实现了北京地区年降水序列的随机模拟，由1724—2019年原序列构建的随机森林模型在训练期和验证期均误差最小，1813—2019年序列在训练期和验证期表现同样优于1951—2019年序列，表明长时间序列在提高降水序列随机模拟精准度方面同样起到关键作用，但在模型验证期依然存在一定误差，需在后续工作进一步丰富拟合因子涉及面和时序尺度，为北京地区长时期年降水序列演变趋势研究提供科学依据。

5 结论

本次研究通过TFPW-BS-Pettitt法和ESMD算法对北京地区1724—2019年等不同降水序列组成成分进行分析，并利用随机森林模型对年降水序列进行随机模拟，得出结论如下：

（1）北京地区296年长降水序列存在 “上升—平稳—下降”的趋势变化特征和2.5～4年、7～15年、25～35年、74年左右和95～100年的准周期波动规律，并且在整个研究时域内存在1770年、1813年、1871年、1893年、1947年和1999年6个突变点。

（2）构建随机森林模型对北京地区年降水量进行随机模拟，其中，模型训练期和验证期平均相对误差绝对值分别小于5%和15%，结果表明随机森林模型拥有较好的模拟效果。随机森林模型作为长期降水序列随机模拟的新途径表现良好，但由于拟合因子是模型构建的关键所在，因此如何选取和筛查科学、合理的拟合因子有待于在后续研究中不断修改和完善。

（3）通过对比分析可知，长时间序列在降水序列成分分析和随机模拟均表现更好，既能检出降水序列隐含的多突变点、更精准更完整的周期尺度和趋势变化规律，更能有效提高随机模拟精度，增强研究逻辑性和说服力。

（4）在传统水文序列成分分析的基础上引入随机模拟，将研究时域从历史时期延伸到未来短期内，增强研究完整性，有助于更好地研究水文时序变化情况、揭示序列演变规律。

致谢：感谢水利部发展研究中心李淼博士在数据收集方面给予的支持和帮助！