鼠笼式异步电机整机模态仿真与实验验证

王栎宁，李名殷，董兴建，皇甫一樊

(1． 上海电气集团上海电机厂有限公司，上海 200240；2． 上海交通大学机械系统与振动国家重点实验室，上海 200240)

0 引言

在“碳达峰、碳中和”大背景下，风力发电这一清洁能源形式具有非常广阔的前景。发电机作为风机的核心部件，其动力学性能关系到整个风力发电系统的可靠性。

构建准确的发电机整机有限元模型对发电机参数设计、性能评估和优化设计有着重大的意义。然而，目前对于发电机的动力学特性研究一般仅局限于部件级[1]，缺少对发电机整机建模的相关研究。传统的有限元建模往往会采用非常细密的网格来刻画发电机定子和转子的铁心部分[2]，这种建模方式会极大地消耗计算资源。

针对上述不足，本文采用各向异性的材料来简化定子和转子的复杂铁心结构，以此来提升计算效率。在部件级建模的基础上，建立了发电机的整机动力学模型，并且采用模态实验来验证本文模型的有效性。

1 有限元模型

本文的研究对象为一台全功率变频的鼠笼式异步发电机。发电机整机的结构非常复杂，如不进行适当的分解与简化，会造成模型过于庞大而无法计算。我们将整机分解为转子、定子铁心和机座这几部分。

1．1 部件级模型

1．1．1 转子

有限元模型通过参数化建模的方式在ANSYS中建立。采用Beam188梁单元模拟阶梯轴，其余部分采用Solid185模拟如图1所示。梁单元采用各向同性材料，阶梯轴到内外环之间的筋也采用各向同性的材料。转子铁心具有复杂的周期性叠片结构形式，如直接建模会造成网格数目巨大。本文采用正交各向异性材料对转子铁心进行建模，大幅减少了单元数目，提升了计算效率。

图1 转子有限元模型

对发电机转子铁心部位进行简化。简化的思路：将其视为正交各向异性材料，利用ANSYS APDL的优化工具进行优化，直到优化后的正交各向异性材料的模态振型与复杂模型一致。

对转子进行实验模态测试，将仿真得到的固有频率与实验测得的固有频率进行对比，如表1所示。从中可以看出，仿真模型具有较高的精度，误差在±4%以内。

表1 转子固有频率误差

1．1．2 定子铁心

采用Beam188梁单元模拟加强筋，其余部分采用Solid185模拟如图2所示。梁单元和压圈采用各向同性材料。与转子铁心类似，定子铁心的齿部、线缆也采用正交各向异性材料来模拟，压圈采用各向同性材料来模拟。

图2 定子铁心有限元模型

对定子铁心进行实验模态测试，仿真与实验得到的固有频率误差如表2所示，固有频率误差在±5%左右，这证明了有限元仿真模型的有效性。

表2 定子铁心固有频率误差

1．1．3 机座

采用Solid185单元对机座模型进行网格划分，其有限元模型如图3所示。

图3 机座有限元模型

对机座进行实验模态测试，实验与仿真的固有频率对比如表3所示。从实验和仿真的模态振型以及固有频率对比可知，仿真有限元模型具有较好的精度，误差在±4%以内。

表3 机座固有频率误差

1．2 整机模型

整机有限元模型如图4所示。冷却器的重量为2 400 kg，假设其不贡献刚度，仅贡献质量，按照集中质量的形式施加到箱体上方的几个角点上。

图4 整机有限元模型

转子与端盖之间的轴承支撑采用MATRIX27单元模拟。定子铁心与机座、转子铁心与轴之间均采用刚性绑定的方式连接。

2 整机模态测试

模态测试系统主要由以下三个部分组成：由力锤构成的激振部分，由传感器、动态测试系统构成的信号测量和数据采集部分，由计算机上的分析软件构成的信号分析和频响函数估计部分。

2．1 测试仪器

本模态测试信号测量与数据采集系统的主体部分是由江苏东华测试有限公司提供的DH8303动态测试分析系统。该系统提供了操作方便的控制分析软件DHDAS，是以计算机为基础的网络型动态信号测试分析系统，应用非常广泛，一套系统就可以完成应力应变和加速度等各种物理量的测试分析。

2．2 测试方法

发电机模态测试过程中采用了单点激励、多点拾振的方法，该方法能够准确地反映出发电机整体的模态参数。模态实验的现场照片如图5所示。

图5 模态实验现场图

为了提高发电机整体振型的辨识度，在发电机端面与机座侧面一共布置了36个测点，每个测点可以读取三个方向的加速度信号，测点分布如图6所示。测点1-9对应大出线盒侧，测点10-18对应小出线盒侧，测点19-27对应轴伸端端面，测点28-36对应非轴伸端端面。

图6 测点分布图

力锤激励点固定为12号测点，发电机经力锤激励，得出每个测点的频响函数。例如，测点28在发电机轴向的频响函数如图7所示，单个的频响图大体能反映出发电机在该方向的固有频率。

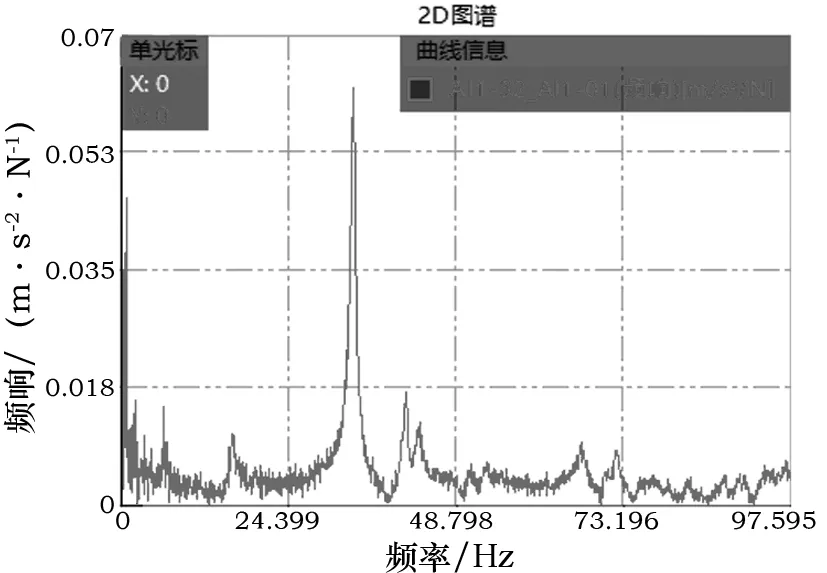
图7 频响函数

3 仿真与实验对比

采用导纳圆法对所有的测点进行频响数据拟合，得到的实验模态前两阶发电机整体振型如图8所示，第1阶振型为轴向振型，第2阶振型为左右摇摆振型。

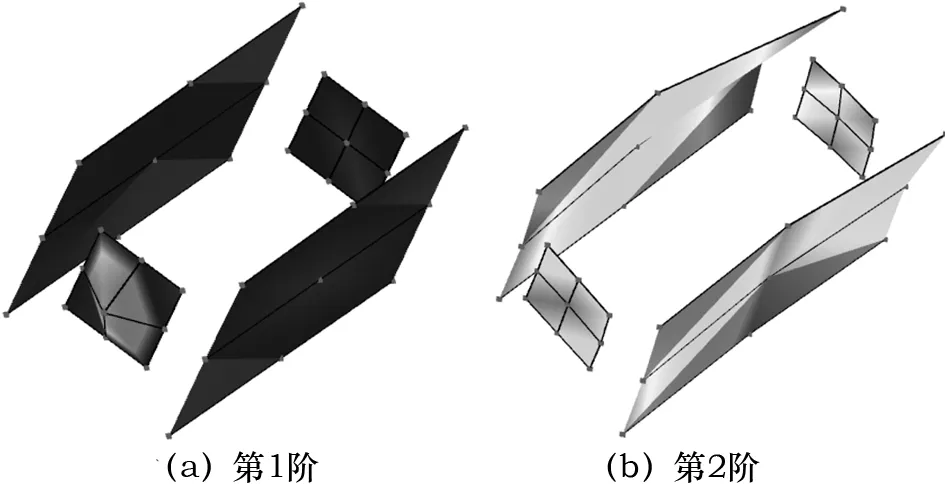
图8 实验得到的模态振型

采用有限元法得到对应实验模态的振型如图9所示。

图9 有限元法得到的模态振型

实验与仿真的固有频率对比如表4所示。从实验和仿真的模态振型以及固有频率对比可知，仿真有限元模型具有较好的精度。

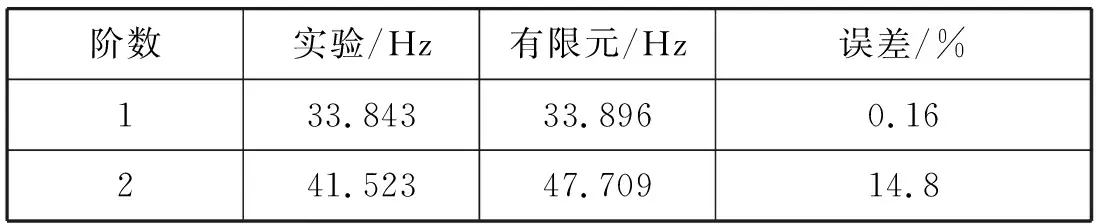
表4 固有频率误差

4 结论

(1) 定子和转子铁心具有复杂的周期性结构，如直接建模会造成网格数目巨大。本文采用正交各向异性材料对铁心进行建模，大幅减少了单元数目，提升了计算效率。

(2) 通过对比仿真与实验得到的模态振型与固有频率可知，本文所建立的有限元模型具有较高的精度。

(3) 本文所提出的发电机整机建模方法为发电机的参数设计、性能评估和优化设计提供了理论基础。