熔融浸渍工艺参数对纤维束渗透率影响的研究

杨一飞，王明欢，李 杰，何亚东，2，信春玲，任 峰*

（1.北京化工大学机电工程学院，北京 100029；2.教育部高分子材料加工装备工程研究中心，北京 100029）

0 前言

纤维增强复合材料相较于传统材料，在比强度和比模量等方面具有显著优势［1］，其中纤维增强热塑性复合材料有更好的韧性和耐热性，而且可以再次回收使用，其应用领域不断扩大［2-3］。在熔融浸渍工艺制备热塑性复合材料过程中，由于热塑性树脂黏度高，存在浸渍困难，熔融浸渍工艺过程难精确描述等问题［4］。渗透率K是综合反映纤维增强体渗透性的参数，数值越小，表明树脂流动过程中受到的阻力越大，浸润纤维越困难，渗透率的研究对实现良好的浸渍尤为重要［5-6］。目前有很多学者做了渗透率相关的研究，主要采取实验或者仿真的方法。张浩等［7］通过实验发现纤维体积分数的增大会减小织物纤维厚度方向渗透率，用于控制纤维厚度并防止纤维变形的刚性构件网孔板层开孔率的增大会减小注射压力对渗透率的影响。Klunker等［8］对不同纤维体积分数和不同注射压力下的碳纤维的厚度方向渗透率进行测量，发现压力对低纤维体积分数时的渗透率有显着影响，而随着纤维体积分数的增加，影响减弱。Fauster 等［9］用一种测量单层单向纤维材料在拉伸载荷作用下渗透率的新方法，到了横向渗透率随拉伸载荷的变化规律。李晨等［10-11］采用Monte Carlo 随机算法建立了微观尺度纤维束内单丝随机排布结构和纤维束内、束外介观尺度结构模型，研究丝束内纤维的随机排列对渗透性和流动特性的影响，结果表明孔隙率对渗透率的影响最为明显。当前确定渗透率的实验，大多都是基于低黏度树脂测定，针对高黏度树脂浸渍纤维束过程中的渗透率K的确定研究很少；纤维束渗透率确定很少考虑工艺参数中纤维束张力与浸渍压力对纤维束孔隙率和渗透率变化的影响。

本文通过设计纤维束渗透率测量装置，模拟连续纤维熔融浸渍工艺过程中高黏度树脂浸渍纤维束过程，研究工艺参数中纤维束张力、浸渍压力对纤维束孔隙率和渗透率的影响。

1 实验部分

1.1 主要原料

聚丙烯，BX3950，密度为0.91 g/cm3，熔体流动速率为160 g/10 min，黏度为（200 ℃）156.5 Pa·s，韩国SK股份有限公司；

玻璃纤维，SE4849，密度为2.62 g/cm3，线密度为2 400 tex，欧文斯科宁（中国）投资有限公司。

1.2 主要设备及仪器

参考熔融浸渍工艺，采用自行设计渗透率的测量装置进行实验，为了尽可能让实验符合实际情况，使用热塑性树脂和连续单向纤维束为原料，渗透率测试装置及实验过程示意图如图1～3 所示。渗透率测试装置主体为柱形，中间有一通孔，内部有环形凹槽可加入树脂，在主体侧壁开细缝作为树脂的浸渍口，树脂通过细缝浸渍纤维。顶盖和底部纤维限位圈通过螺纹安装在装置主体上，纤维缠绕部位底部有顶板，可撬起顶板方便取下浸渍后的纤维，顶盖有气路接口，主体底部有热电偶接口，与控制柜连接进行控温，纤维固定螺栓安装在顶盖和主体底部；

图1 纤维缠绕装置Fig.1 Fiber winding device

扫描电子显微镜（SEM），TM4000 II，日立（中国）有限公司；

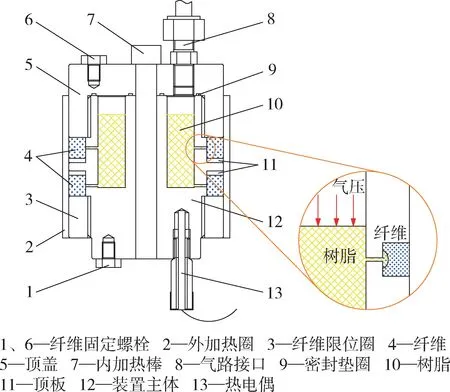
图2 渗透率测试装置Fig.2 Permeability testing device

图3 装置实物图Fig.3 Device physical diagram

三滑轮张力传感器，JZHL-3-50N，蚌埠传感器系统工程有限公司；

PLC，SIMATIC S7-1200，西门子（中国）有限公司。

1.3 样品制备

本实验主要考虑不同纤维束张力和浸渍压力对渗透率的影响，通过改变纤维缠绕分散辊的数量，调整纤维的张力，三滑轮张力传感器通过PLC 连接电脑读取实时张力数据，将纤维均匀缠绕在装置上，并将纤维末端固定保持张力。加入树脂后加热到设定温度，缓慢通入气体到达设定气压，以气压作为树脂浸渍压力，达到设定时间后关闭气体和加热，静置冷却后取下完成浸渍的纤维试样。

在本实验的浸渍过程中存在3个浸渍方向，本文测量的是与浸渍压力方向相同的浸渍深度，将浸渍压力、纤维束张力设为实验参数。浸渍时间为t=300 s，温度为200 ℃，纤维束张力取4、6、8 N，每种张力的浸渍压力从0.06～0.18 MPa，间隔0.02 MPa。实验分组如表1所示。

表1 实验分组Tab.1 Experimental grouping

1.4 性能测试与结构表征

渗透率的测定：得到实验试样后，去除试样表面未浸渍树脂的纤维，通过游标卡尺测得径向最厚位置的数值即为浸渍深度，如图4所示。

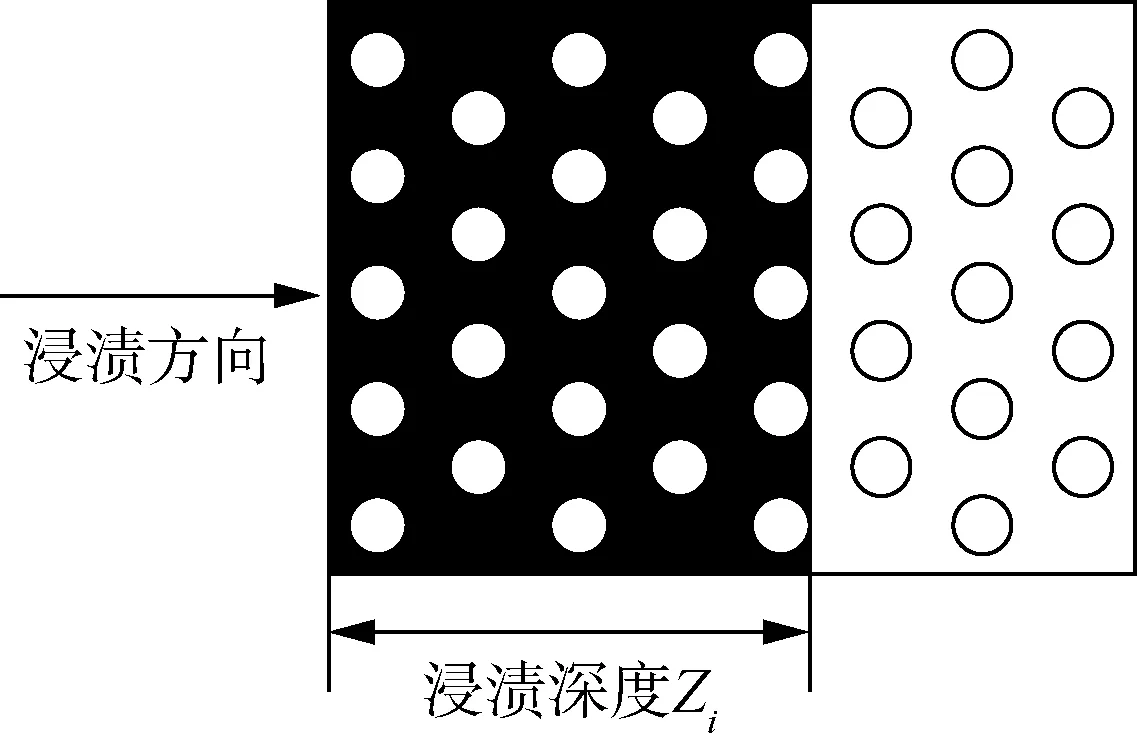
图4 纤维束浸渍深度Fig.4 Fiber bundle impregnation depth

达西定律可描述树脂浸渍纤维过程，如式（1）所示：

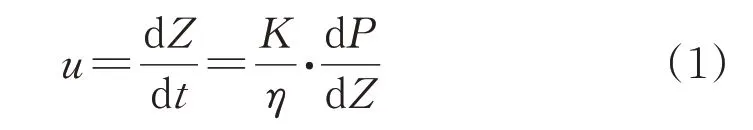
式中u——浸渍速率，m/s

t——浸渍时间，s

Z——浸渍深度，m

K——渗透率，m2

P——浸渍压力，Pa

η——熔体黏度，Pa·s

对达西定律进行积分，可得式（2），通过此式算出渗透率K。

纤维孔隙测量：沿浸渍深度方向切割制备截面，打磨平整后用SEM 观察浸渍截面，如图5 所示，在远离浸渍口、靠近浸渍口和左右边缘每个位置拍摄显微图像，通过Image-Pro Plus 软件处理，可得出孔隙总面积，孔隙总面积与截面总面积之比即为孔隙率，判断不同纤维束张力和浸渍压力下对纤维孔隙产生的影响。

图5 SEM观察截面取样位置Fig.5 Sampling position of SEM observation section

2 结果与讨论

2.1 实验结果拟合方程

每组条件取4 个数据，根据式（3）求出每组的浸渍深度平均值Z，具体数据如表2所示。

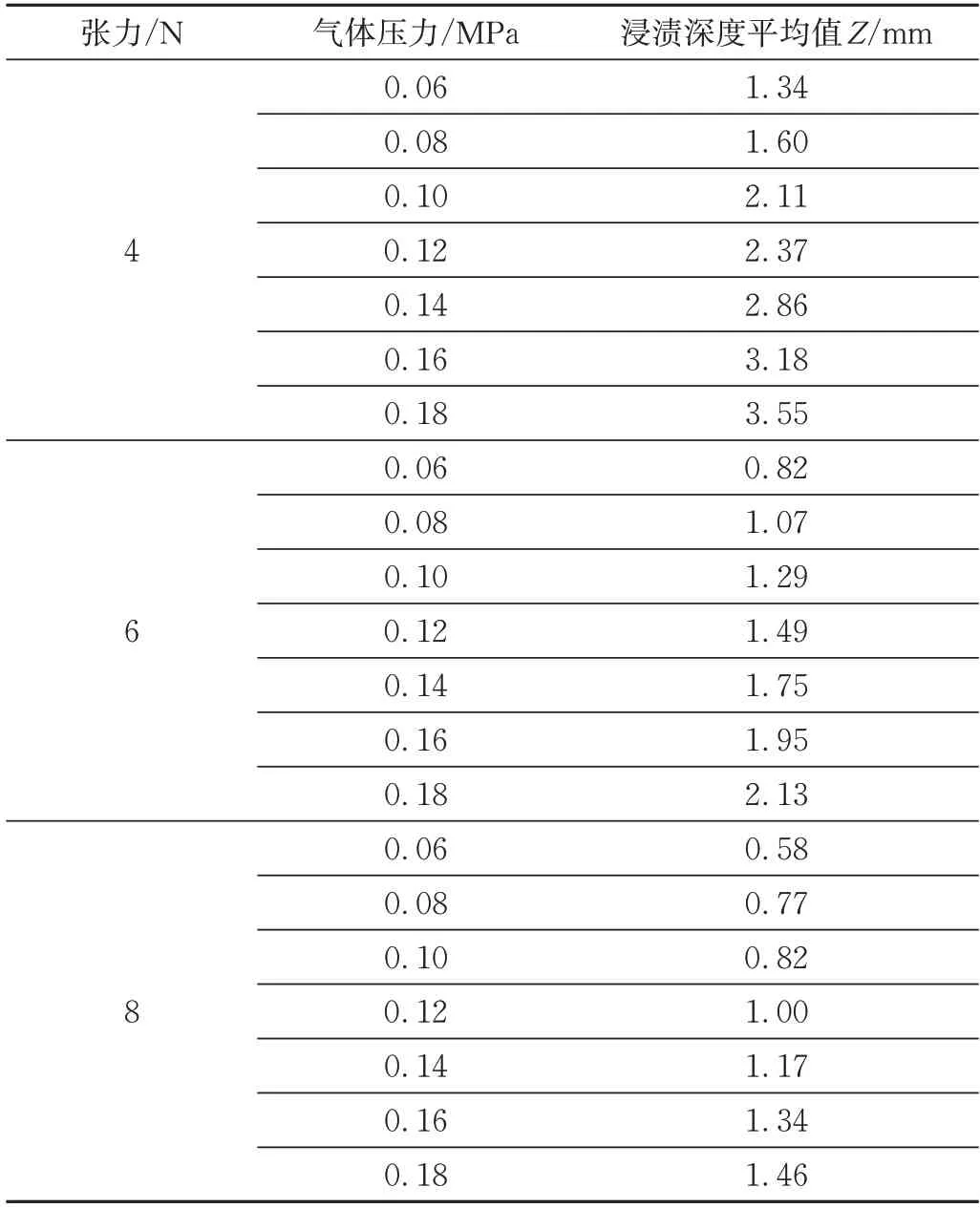
表2 浸渍深度平均值ZTab.2 Average value of immersion depth

式中Zi——每个测量处的浸渍深度，mm

将浸渍深度Z和其他参数代入式（2）即中计算出渗透率K，以渗透率K为因变量，以纤维束张力F和浸渍压力P为自变量，使用Matlab进行编程拟合，拟合结果如式（4）所示：

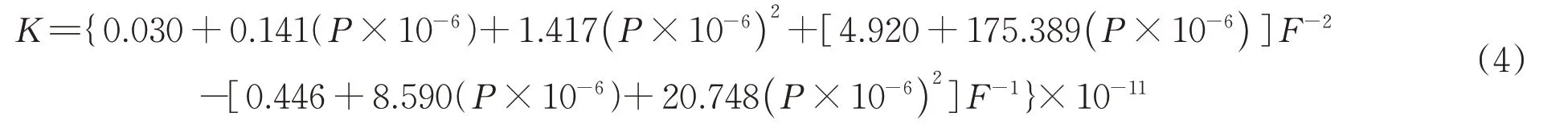
由Matlab 得出拟合曲面如图6 所示，不同压力和不同张力情况下拟合曲线如图7、8所示，可以看出拟合方程与实验结果规律相符，且误差较小。

图6 渗透率拟合曲面Fig.6 Permeability fitting surface

由图7、8 可以看出，在本实验中，纤维束张力相同的情况下，浸渍压力越大渗透率越高，浸渍压力相同时，纤维束张力越大渗透率越低。并且在纤维束张力为4 N 时，渗透率随浸渍压力升高的趋势十分明显，而纤维束张力从4 N 增大到8 N 时，渗透率随浸渍压力增大而升高的趋势逐渐降低，浸渍压力对渗透率的影响变小。这是由于孔隙率随着张力的增大而减小，随浸渍压力的增大而增大，纤维束受张力和压力引起孔隙变化的示意图如图9 所示，单向纤维在浸渍过程中，横向受到树脂浸渍给到的压力，纤维会向树脂流动方向产生弯曲变形，使纤维间孔隙增大，渗透率也增大。在纤维束张力较大时，孔隙率很小，其变化对渗透率的影响也会减小，因此在张力较大时，渗透率随浸渍压力增大而增大的趋势逐渐减小。

图7 渗透率拟合曲线与实验值对比Fig.7 Comparison of the permeability fitting data with the experimental value

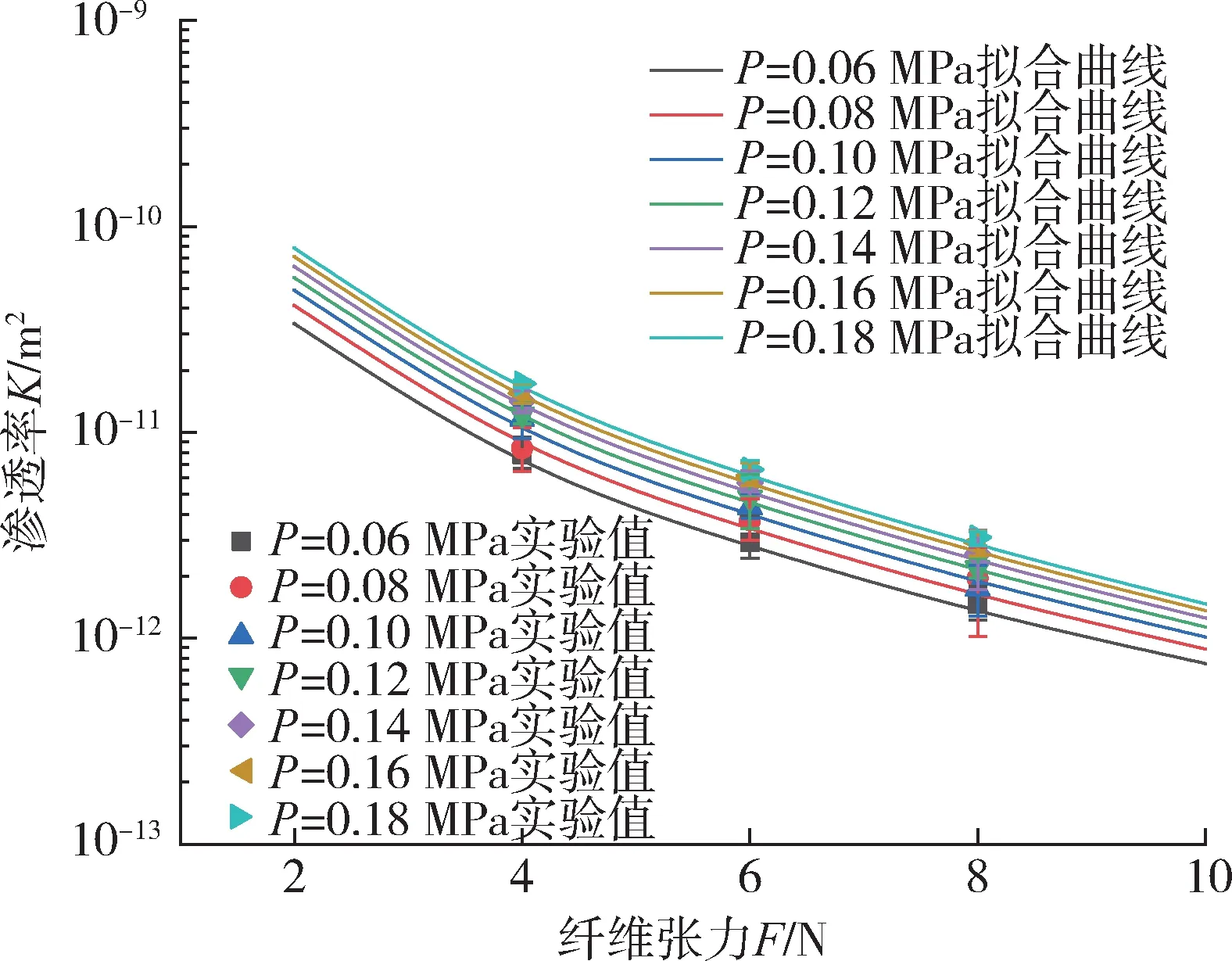
图8 纤维束张力和渗透率的关系Fig.8 The relationship between permeability and fiber bundle tension

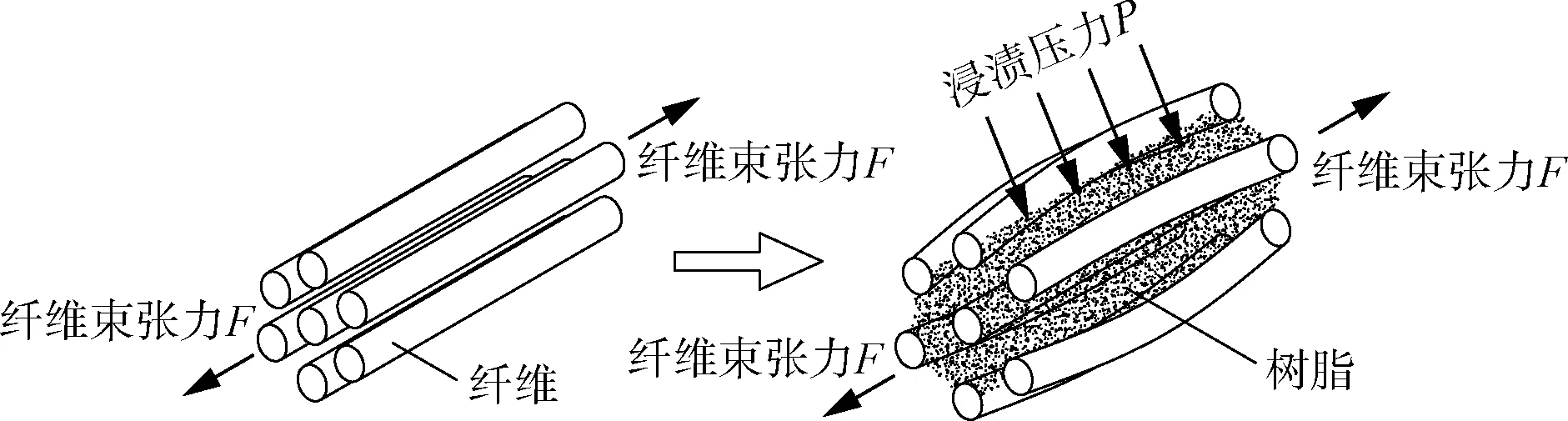
图9 因压力和张力引起纤维变形导致孔隙的变化Fig.9 Changes in porosity caused by fiber deformation due to pressure and tension

2.2 纤维束张力和浸渍压力对孔隙率的影响

图10为试样截面的SEM 照片，可以看到不同条件和不同位置的孔隙率有所不同。通过Image-Pro Plus软件处理计算后不同张力下的截面不同位置孔隙率结果如图11 所示，由图可知靠近浸渍口位置的孔隙率大于其他位置的孔隙率，这说明了树脂的压力导致纤维变形确实使纤维局部体积分数有了较明显的减小。

图10 不同参数下不同位置的SEM照片Fig.10 SEM of various positions under different conditions

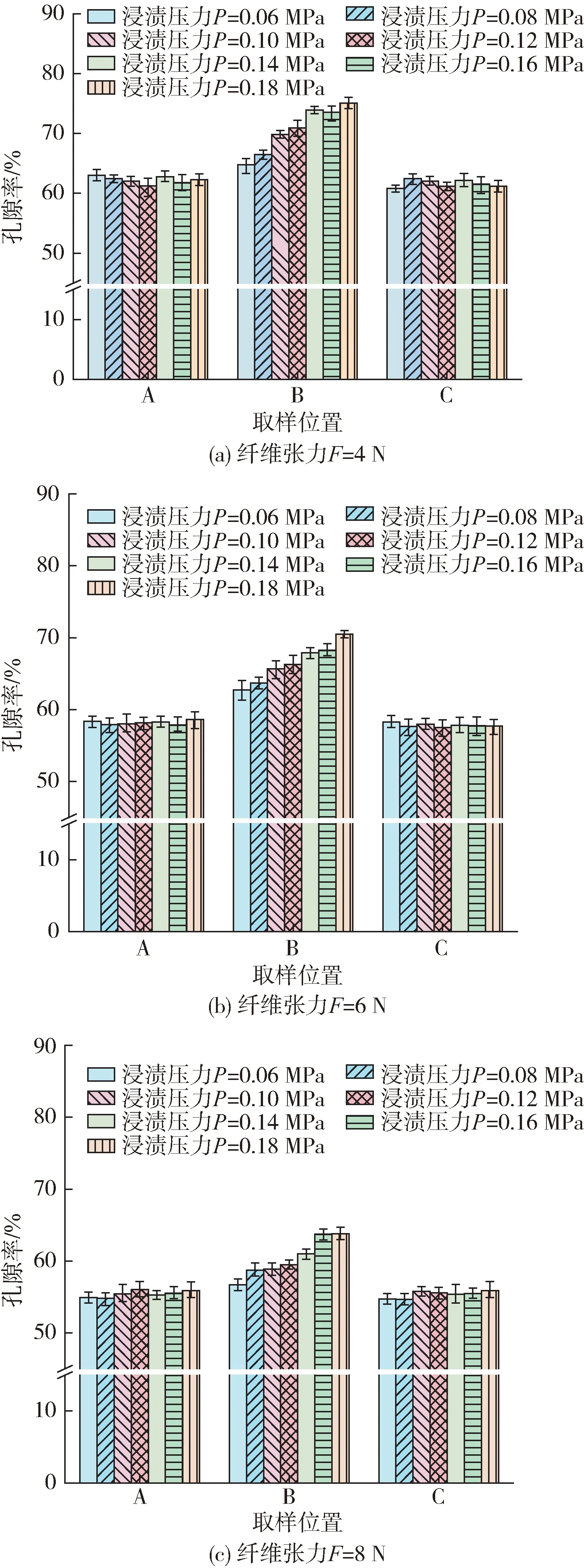
图11 不同纤维束张力下各位置的孔隙率Fig.11 Porosity at each position under different fiber bundle tensions

图12 为不同位置孔隙率随浸渍压力变化的关系，可以看出，位置A 和C 的孔隙率几乎不随浸渍压力变化而变化，而位置B 孔隙率随着浸渍压力的增大而减小，且孔隙率随浸渍压力增大的趋势随着纤维束张力的增大而减小。可能是由于张力较低时，纤维轴向约束小，纤维之间的空隙较大，纤维也更容易向树脂流动方向变形，使局部孔隙更容易增大；而张力较高时，纤维轴向约束大，纤维之间的空隙也小，纤维的弯曲更加困难，使孔隙变化较小。

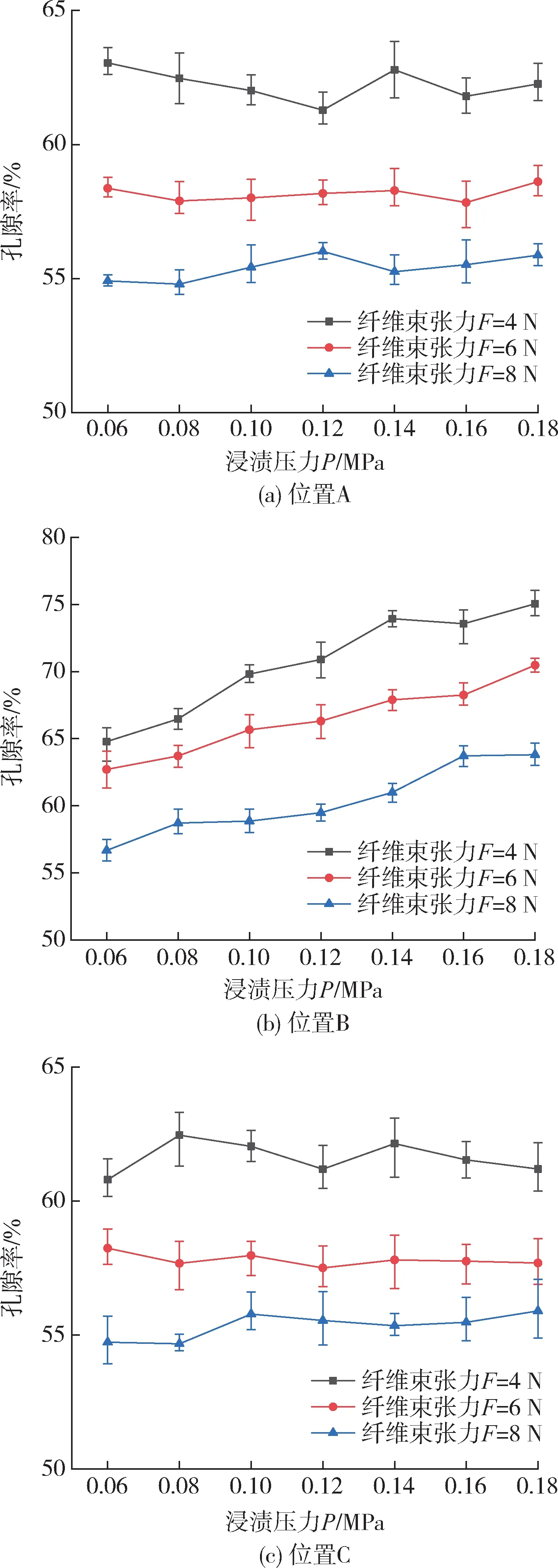
图12 不同位置处的孔隙率Fig.12 Porosity at different locations

2.3 渗透率拟合方程的验证

熔融浸渍工艺中的弯曲流道模具结构如图13所示，在弯曲流道模具中，模具通过楔形结构收敛建压，使树脂浸入纤维间隙中。同时树脂对纤维有不可忽略的黏性拖曳力，所以随着楔形区的增加，纤维束所受张力逐渐增加，因此每经过一个楔形区纤维束的渗透率都会变小。不同温度下树脂黏度不同，使楔形区浸渍压力也不相同，渗透率也会发生改变。而在袁满［12］建立的浸渍模型中，采用Kozeny-Carman 方程计算渗透率，没有考虑楔形区的浸渍压力和纤维束张力对纤维孔隙产生影响，进而影响渗透率，使理论值与实验值之间存在差距。根据文献［12］，浸渍压力表达式如式（5）所示。

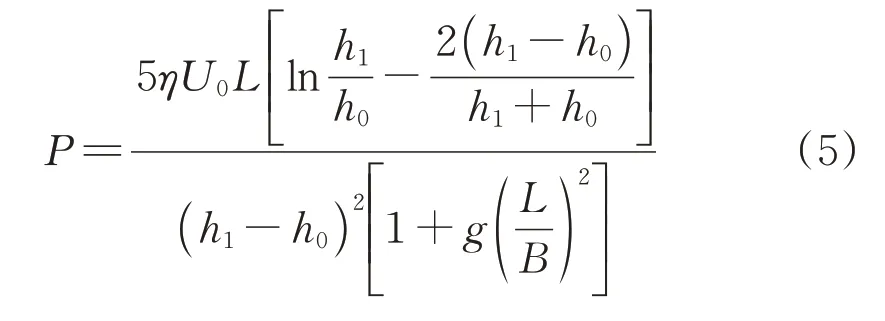
图13 模具楔形区结构Fig.13 Schematic of mold wedge structure

式中h1——楔形区入口高度，m

h0——楔形区出口高度，m

L——楔形区长度，m

B——纤维束展宽，m

U0——牵引速度，m/s

g——只与楔形区进出口高度有关的结构系数浸渍程度的表达式如式（6）所示：

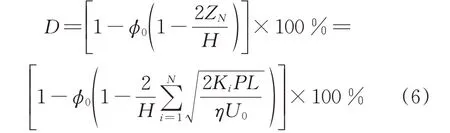
式中D——浸渍程度，%

H——纤维束宽度，m

ϕ0——纤维束初始孔隙率

N——楔形区个数

ZN——纤维束单侧浸渍深度，m

Ki——第i个楔形区的渗透率

陈剑昭［13］给出了纤维在模具中所受的黏性拖曳力的关系式如式（7）所示：

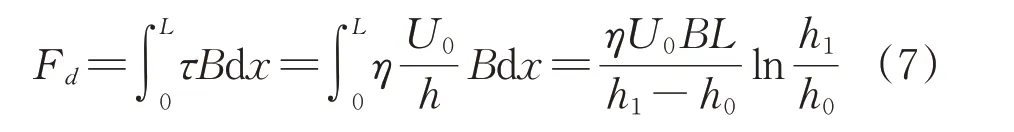
式中Fd——黏性拖曳力，N

τ——黏性拖曳应力，Pa

h——楔形区任意位置处的高度，m

不同温度下的树脂黏度η可通过旋转流变仪测出，温度越高，树脂黏度越低。将式（4）、（5）联立，代入不同温度下的树脂黏度和纤维束张力等其他参数，可计算出各温度的渗透率。图14示出了不同温度下第一个楔形区分别采用拟合方程和Kozeny-Carman 方程计算的渗透率，可以看出由于温度变化引起树脂黏度变化，使浸渍压力和纤维束张力改变，影响了纤维孔隙率，从而使渗透率也发生改变，与文献［12］采用Kozeny-Carman方程计算相比，会更加接近实际情况。

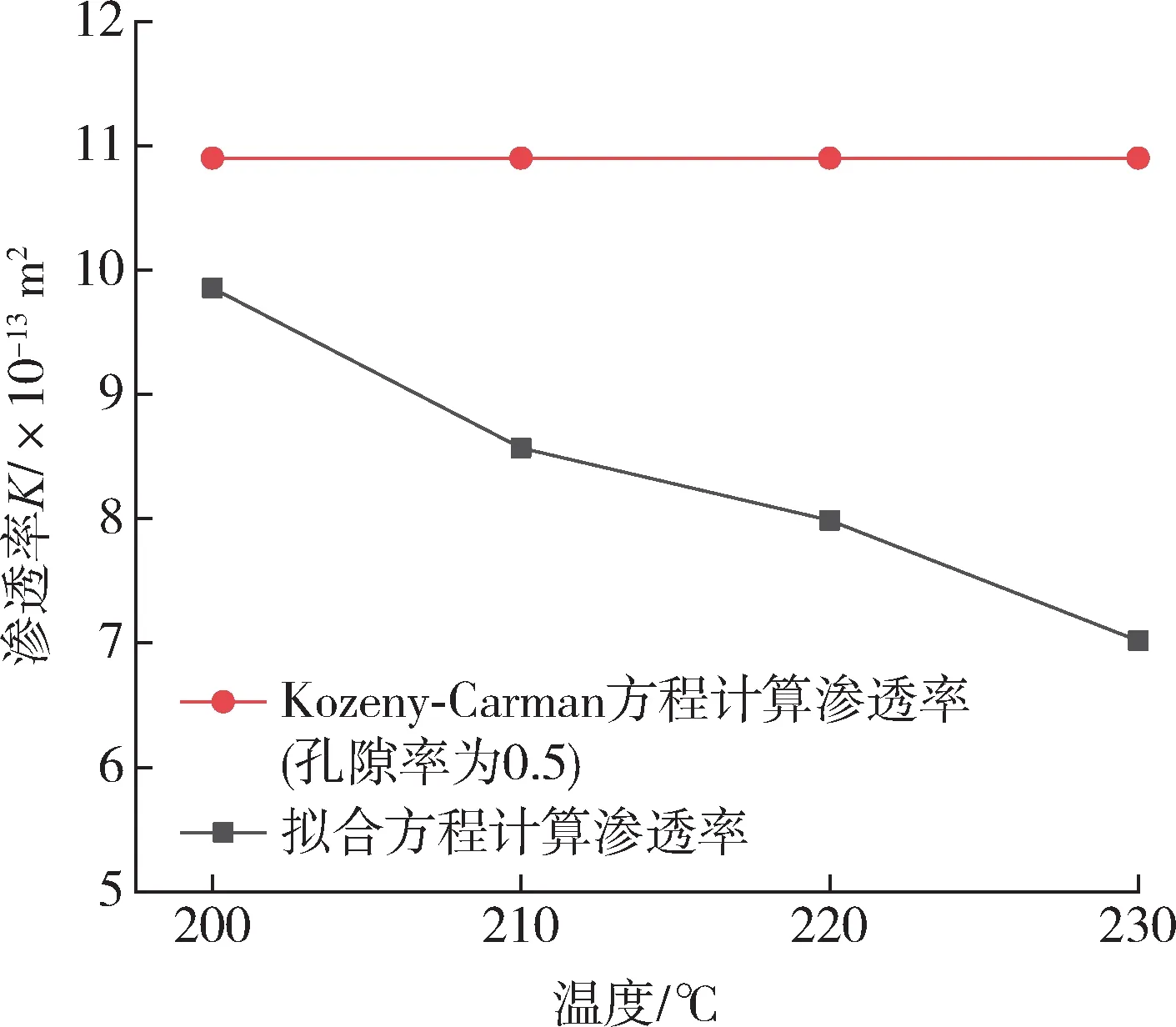
图14 不同温度下第一个楔形区拟合方程与Kozeny-Carman方程计算渗透率的对比Fig.14 Comparison of the first wedge-shaped area number fitting equation and that of Kozeny-Carman for calculating permeability at different temperature

将采用拟合方程计算的渗透率代入式（6）中，得出的浸渍程度理论值与袁满［12］论文中的理论值和实验值对比，如图15所示，不同计算方法所得浸渍程度理论值与实验值误差如图16 所示，可以看到采用本文拟合方程计算渗透率后得出的浸渍程度理论值与实验值误差在0.4%左右，并且随着温度的增加误差逐渐减小，低于采用Kozeny-Carman 方程计算的理论值，所以采用拟合方程计算渗透率能更好的反映实际规律，证明渗透率拟合方程式是可靠的。但由于浸渍模具中纤维束孔隙率的变化情况较为复杂，拟合公式只考虑了浸渍压力和纤维束张力的影响，所以仍存在误差。

图15 不同温度下浸渍程度理论值与实验值的对比Fig.15 Comparison of theoretical values and experimental ones of impregnation degree at different temperature

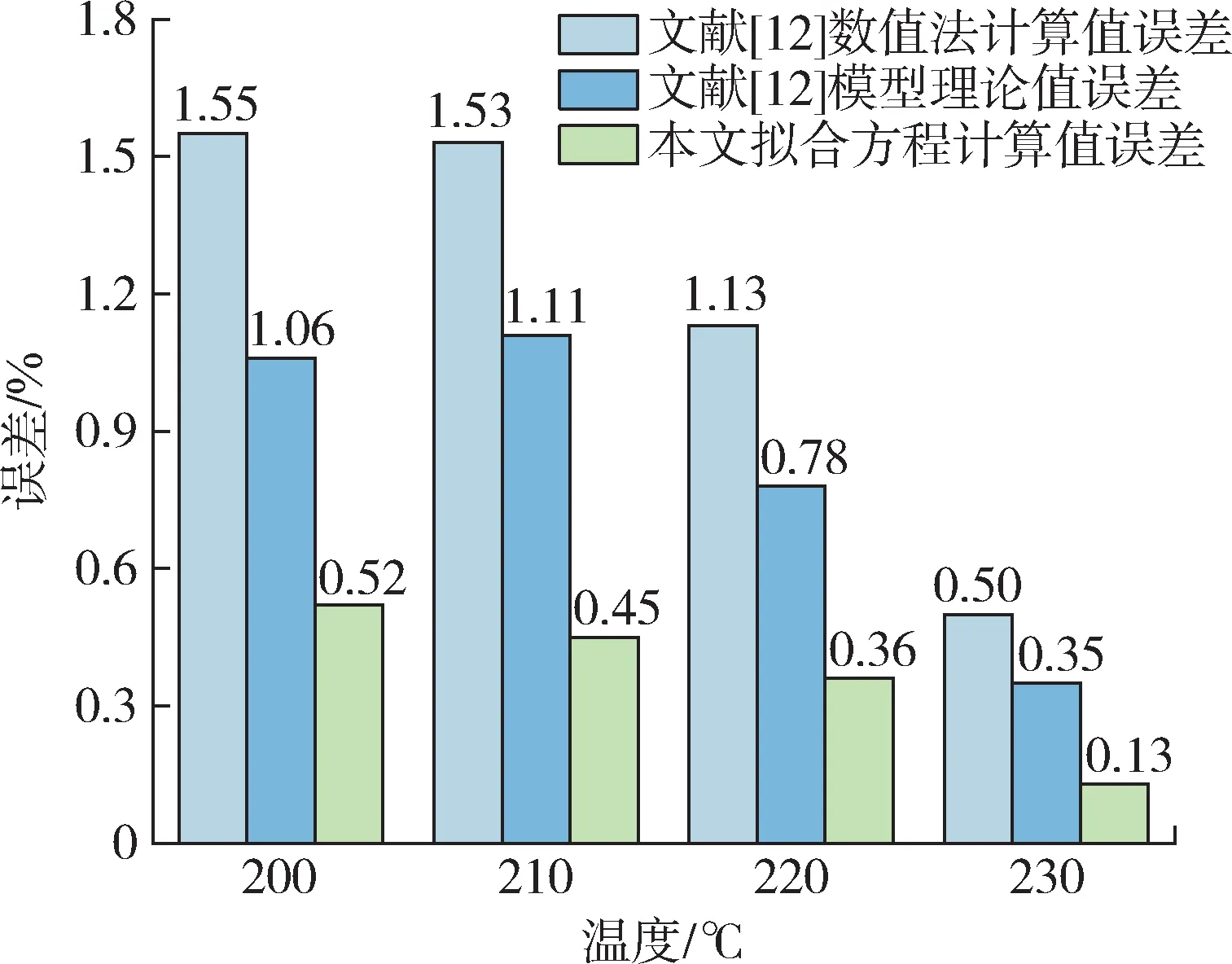
图16 不同计算方法理论值与实验值的误差Fig.16 The error between theoretical values from different calculation methods and experimental ones

3 结论

（1）设计了渗透率测量装置，对高黏度树脂浸渍纤维束的渗透率进行了测量。结果表明，浸渍压力相同时，纤维束张力从4 N增大到8 N的过程中，渗透率逐渐降低，浸渍压力从0.06 MPa 增大到0.18 MPa 的过程中，渗透率逐渐增大，但增大幅度随张力增大而减小；

（2）对纤维束张力、浸渍压力和渗透率之间的关系进行拟合，通过将采用拟合方程计算渗透率后得出的浸渍程度与前人建立模型理论值和实验值的比较，误差在0.4 %左右，与前人相比误差降低了1 %～0.2%，表明拟合结果能较准确预测高黏度树脂浸渍纤维束的渗透率。