基于M型型钢装配式钢筋混凝土剪力墙的有限元分析
陈 飞,杨青顺,2*,卫 骏,周乐祥,王 清
(1.青海大学土木工程学院,青海 西宁 810016; 2.青海省建筑节能材料与工程安全重点实验室,青海 西宁 810016;3.北京中清恒业科技开发有限公司,北京 100000)
剪力墙作为高层建筑结构抗震的关键构件,为整体建筑结构提供抗侧刚度以及承载力,在框剪结构和剪力墙结构中发挥着重要作用。随着我国对于装配式建筑的大力提倡,装配式钢筋混凝土剪力墙在实际工程中的应用越来越广泛[1-4]。近年来,众多学者对装配式钢筋混凝土剪力墙进行了研究。吕西林等[5]、朱爱萍等[6]通过在剪力墙墙体内埋置钢板,提高了剪力墙的整体承载能力、变形能力和耗能能力。聂建国等[7]证实双钢板-混凝土剪力墙比单钢板-混凝土剪力墙的延性及耗能能力更优。陈以一等[8]利用预留裂缝来控制裂缝的发展,改进了剪力墙的受力特性,提高了剪力墙的抗震性能。叶露等[9]将加劲肋和冷弯薄壁型钢梁柱连接成钢框架,提高了剪力墙前期的抗剪刚度、承载力和耗能能力。
本文以乔东需[10]M型型钢组合墙体抗震性能试验结果为基础,对MSSCW1、MSSCW3、MSSCW4、MSSCW6 4组试件建立了有限元模型,通过改变轴压比、剪跨比及型钢厚度等参数,进一步研究M型型钢装配式钢筋混凝土剪力墙的受力性能,为其在实际工程中的应用提供理论依据。
1 试验概况
M型型钢组合墙(MSSCW)[10]中墙体组成部分由加载梁,暗柱,中间墙及地梁四部分组成,采用M型型钢(简称型钢)代替纵向分布筋,尺寸见图1[10]、图2[10]、图3[10]。
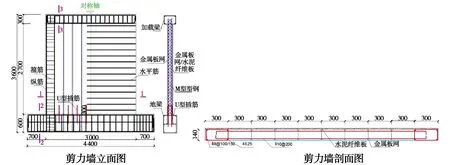
图1 水平筋间距200 mm组合剪力墙试件Fig.1 Composite shear wall specimen with horizontal bar spacing of 200 mm
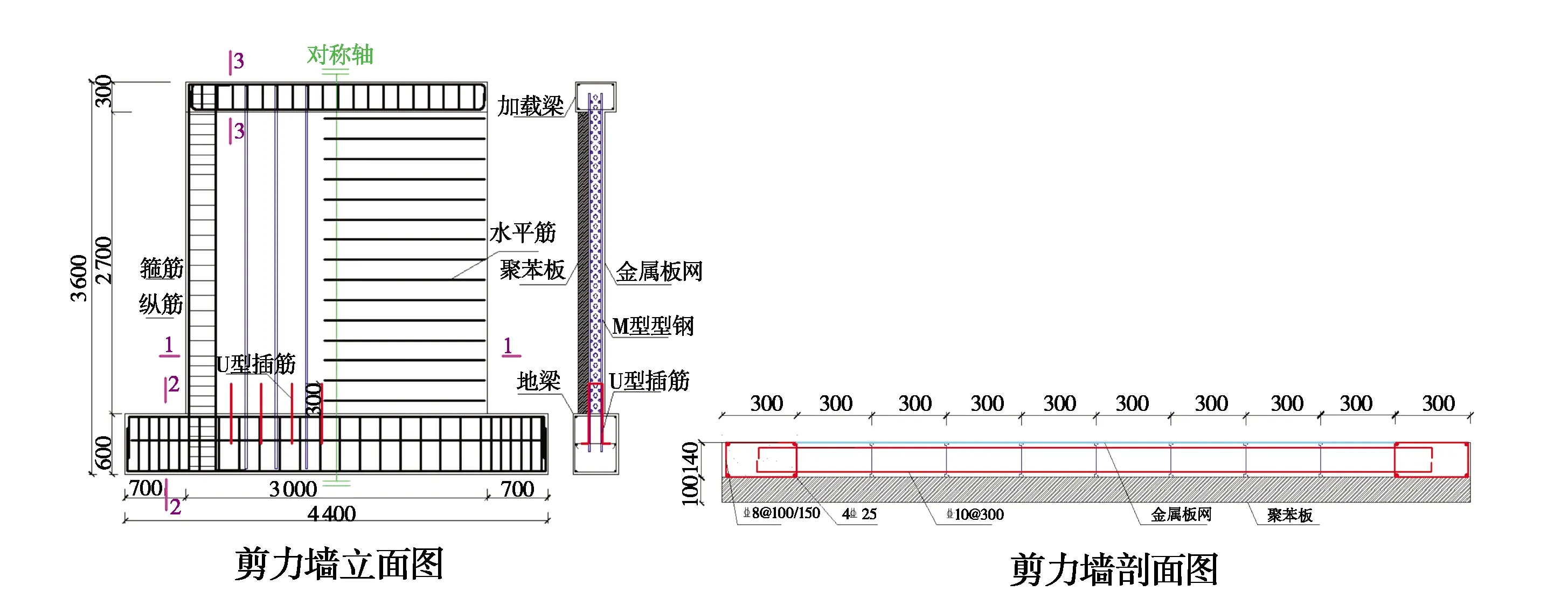
图2 水平筋间距300 mm组合剪力墙试件Fig.2 Composite shear wall specimen with horizontal bar spacing of 300 mm
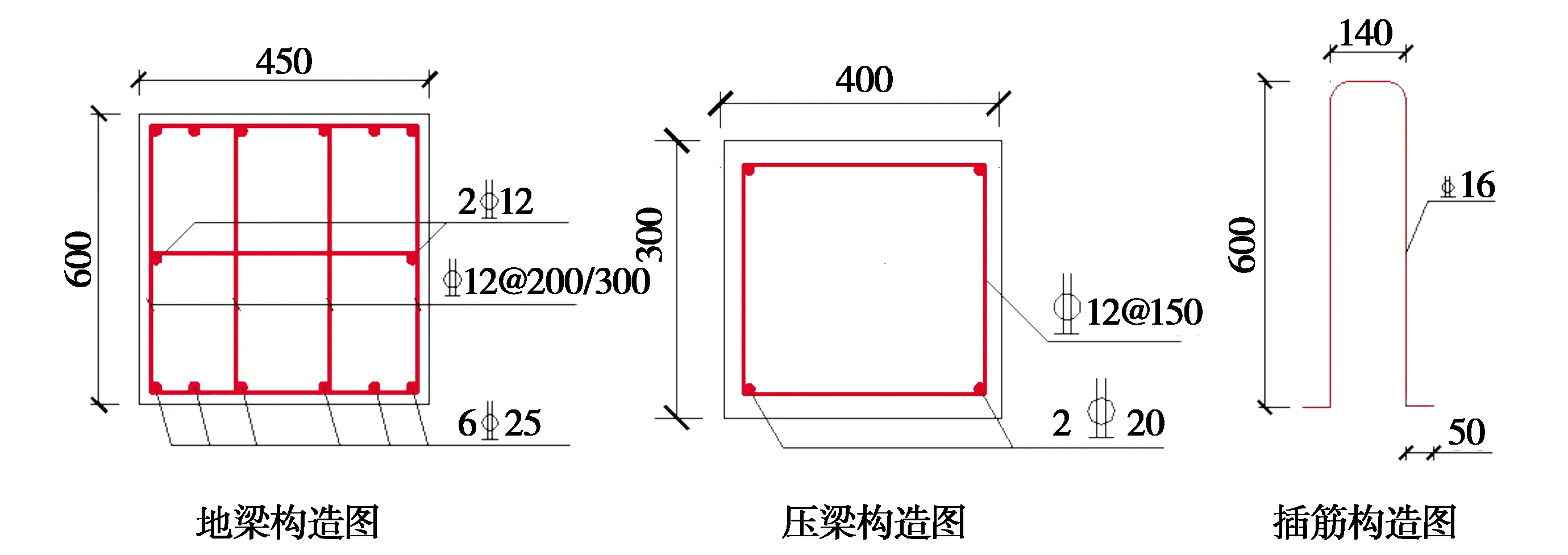
图3 上下梁构造Fig.3 Structure diagram of upper and lower beams
2 有限元模型的建立
2.1 几何模型的建立
用MSC MARC有限元软件选取M型型钢组合墙体[10]中的4组试件MSSCW1、MSSCW3、MSSCW4、MSSCW6建立有限元模型,模型参数变量[10]见表1。该模型采用分离式模型进行模拟,混凝土单元采用7号实体单元模拟,钢筋采用9号桁架单元模拟,型钢采用139号薄壳单元模拟,将桁架单元及薄壳单元通过MSC MARC有限元软件提供的“Insert”功能嵌入混凝土单元中[11]。边界荷载主要为底部位移约束,轴压力分别为1 000、900 kN。在梁左端选取一节点作为加载点。

表1 模型参数变量Tab.1 Parameter variables of the model
2.2 混凝土本构模型
混凝土本构关系根据文献[8]、《混凝土结构设计规范》[12]、文献[13]进行取值。泊松比为0.2,弹性模量为3.0×104N/mm2,受拉软化模量为弹性模量的0.1倍,裂面剪力传递系数为0.125。混凝土轴心抗压强度和轴心抗拉强度根据文献[10]中的混凝土材性试验取值。
2.3 钢材本构模型
钢材的本构关系采用弹性—屈服模型(双线型模型),屈服后的钢材简化为理想弹塑性模型。钢筋、型钢本构关系根据文献[11]、《混凝土结构设计规范》[12]、《钢结构设计规范》[14]进行取值。型钢弹性模量为2.06×105N/mm2,泊松比为0.3;钢筋弹性模量为2.0×105N/mm2,泊松比为0.3;钢材受拉软化模量为弹性模量的0.1倍。其中,钢筋、型钢屈服强度及极限强度根据文献[10]中钢材材性试验取值。钢材的屈服准则为Von-Mises屈服准则,采用各向同性硬化规律。
2.4 加载方式
有限元模拟加载方式仅采用位移控制加载,首先以水平位移3 mm为级数进行循环加载,每级循环3次;当水平位移达到18 mm时,以水平位移6 mm为级数进行循环加载,每级循环3次,依据试验结果,水平位移加载至48 mm时结束加载。
3 有限元模型验证
图4为提取有限元模拟时4组试件在反复加载过程中剪力墙各部位的应变云图。
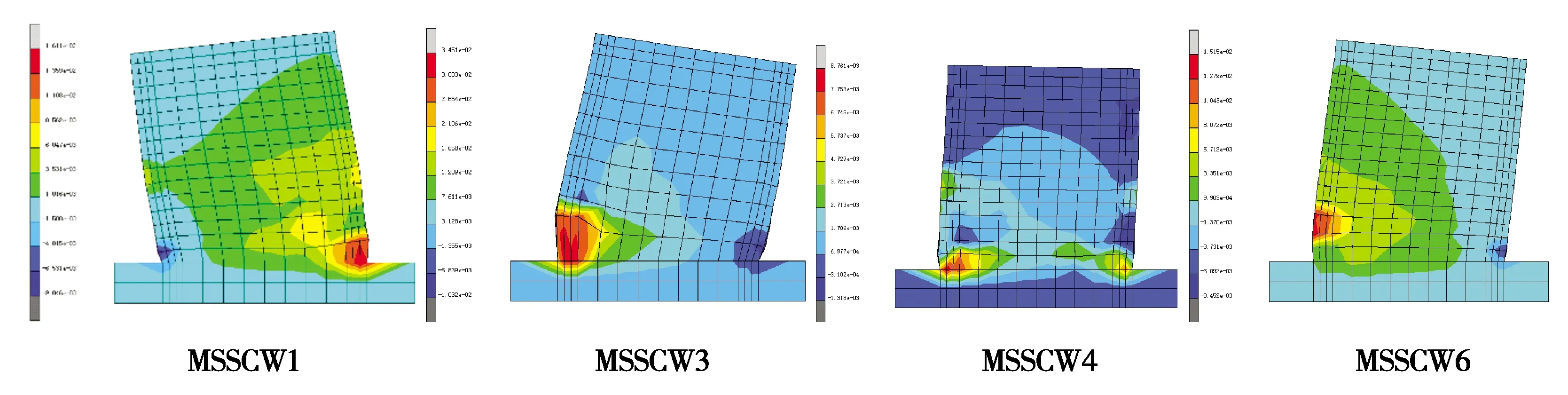
图4 有限元模拟试件应变云图Fig.4 Strain nephogram of finite element simulation specimens
由图4可知,有限元模拟中试件的破坏位置与试验中墙体的破坏位置是一致的,且有限元模拟中水平抗剪屈服荷载和峰值荷载对应位移与试验结果吻合良好。
提取有限元模拟中的数据,利用origin图形处理软件处理4组试验数据和模拟数据,两者之间滞回曲线以及骨架曲线对比图如图5和图6所示。
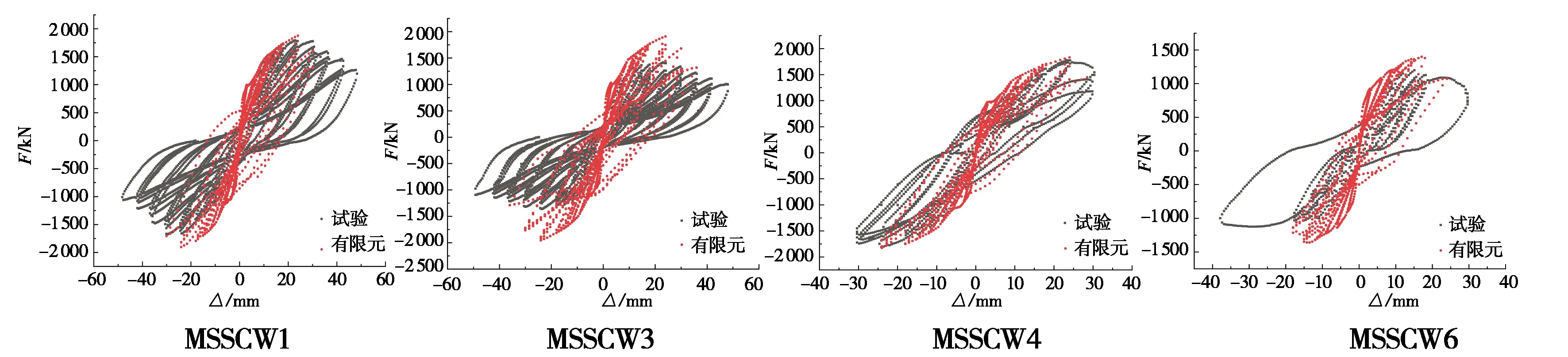
图5 试验与有限元模拟的滞回曲线对比图Fig.5 Comparison of hysteresis curves between test and finite element simulation

图6 试验与有限元模拟的骨架曲线对比图Fig.6 Comparison of skeleton curves between test and finite element simulation
由图5和图6可知,有限元模拟的滞回曲线面积比试验的滞回曲线面积饱满,这是因为在试验反复加载过程中,剪力墙中的试件出现了累计损伤,型钢及钢筋与混凝土之间的滑移会持续增大,而在模拟中试件处于理想状态,就避免了这种现象。在4组骨架曲线试验与模拟计算值对比中,弹性阶段试验值与模拟值刚度基本一致,这是因为此时试验中型钢与混凝土共同受力工作,基本未出现滑移现象;在进入弹塑性阶段后,模拟值刚度略大于试验值,这是因为试验过程中型钢及钢筋与混凝土之间出现了滑移现象,而在模拟中则未考虑这种情况。通过综合对比滞回曲线及骨架曲线,发现两者趋向规律基本一致,峰值荷载及峰值位移基本相同,表明采用的有限元模型可以有效模拟试验的受力性能,并且可以分析该类组合剪力墙的变换参数。
4 参数分析
对M型型钢装配式钢筋混凝土剪力墙做进一步的模拟分析,通过改变型钢厚度、轴压比及剪跨比等参数得到18组模型。在高层建筑中,除了标准层层高3.6 m外,当地上一层层高超过5 m时,剪力墙的剪跨比会随之增加。因此,本研究除了对小剪跨比(λ=0.95,λ=1.5)的剪力墙进行研究外,对大剪跨比(λ=2.0,λ=3.0)剪力墙的承载力及延性性能也做了研究。各模型参数变量如表2所示。
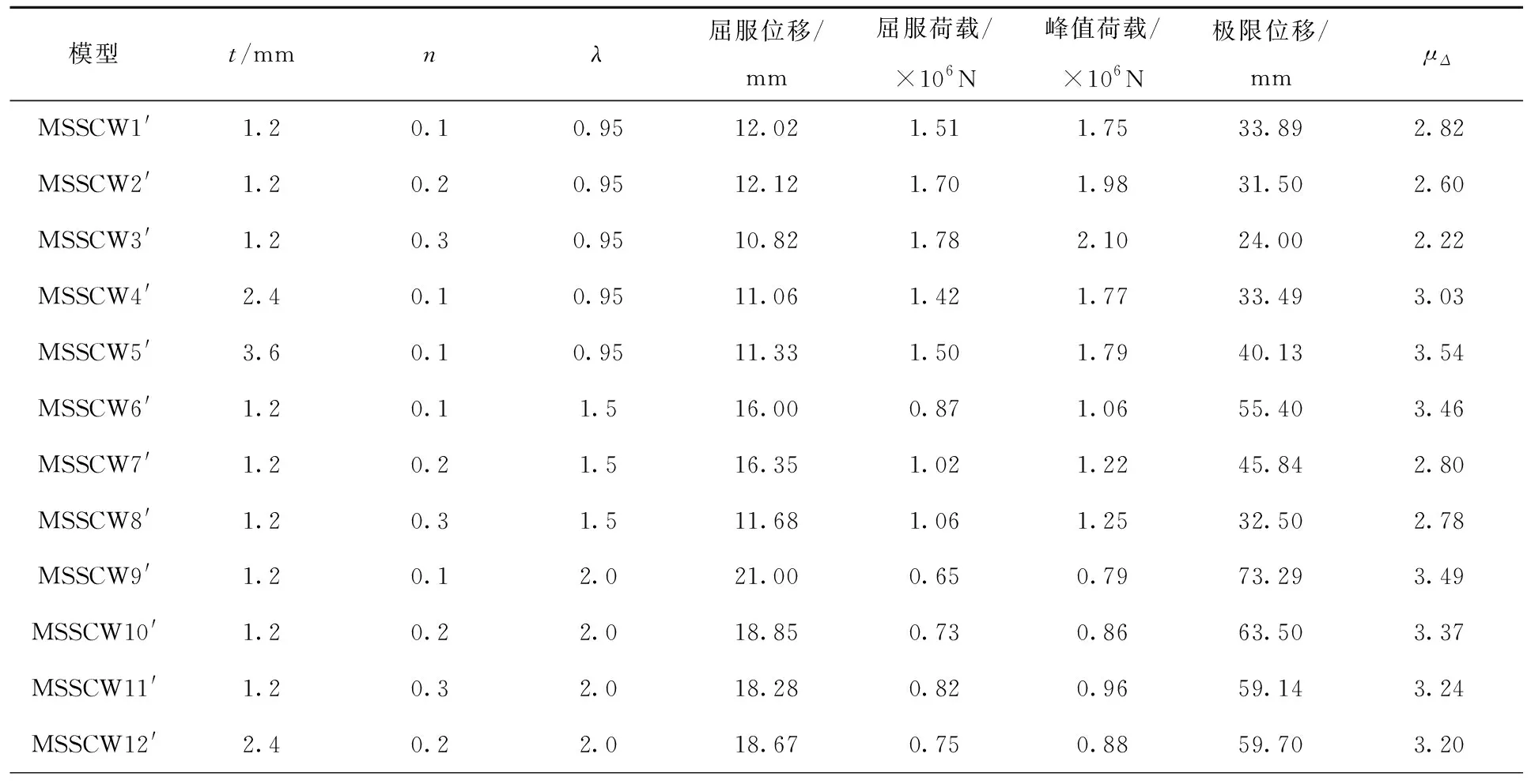
表2 模型参数Tab.2 Model parameters
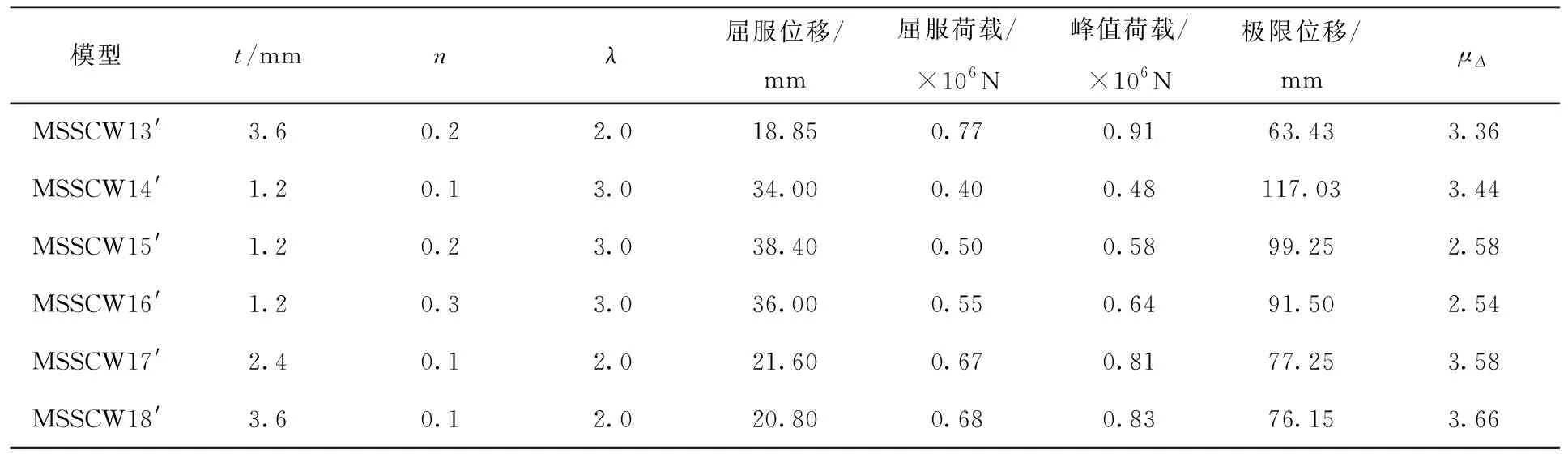
表2(续)
4.1 剪跨比参数变化结果分析
在保持剪力墙横截面不变的条件下,改变剪力墙的高度及加载点,得到的剪跨比分别为0.95、1.5、2.0、3.0。在轴压比不同而型钢厚度不变的条件下,通过改变剪力墙的剪跨比发现,剪跨比越大,抗侧刚度则越小,从而导致水平承载力随之减小。与模型MSSCW1′、 MSSCW2′、 MSSCW3′(剪跨比为0.95)相比,模型MSSCW6′、 MSSCW7′、 MSSCW8′(剪跨比为1.5)的水平峰值荷载降低了38.38%~40.48%,模型MSSCW9′、 MSSCW10′、 MSSCW11′(剪跨比为2.0)水平峰值荷载降低了54.29%~56.57%,模型MSSCW14′、 MSSCW15′、 MSSCW16′(剪跨比为3.0)水平峰值荷载降低了69.52%~72.57%。通过分析此类型剪力墙发现,当剪跨比未超过2.0时,位移延性系数随剪跨比增大而增加;当剪跨比超过2.0时,位移延性系数开始出现下降趋势。M型型钢装配式钢筋混凝土剪力墙在不同剪跨比条件下的骨架曲线如图7所示。
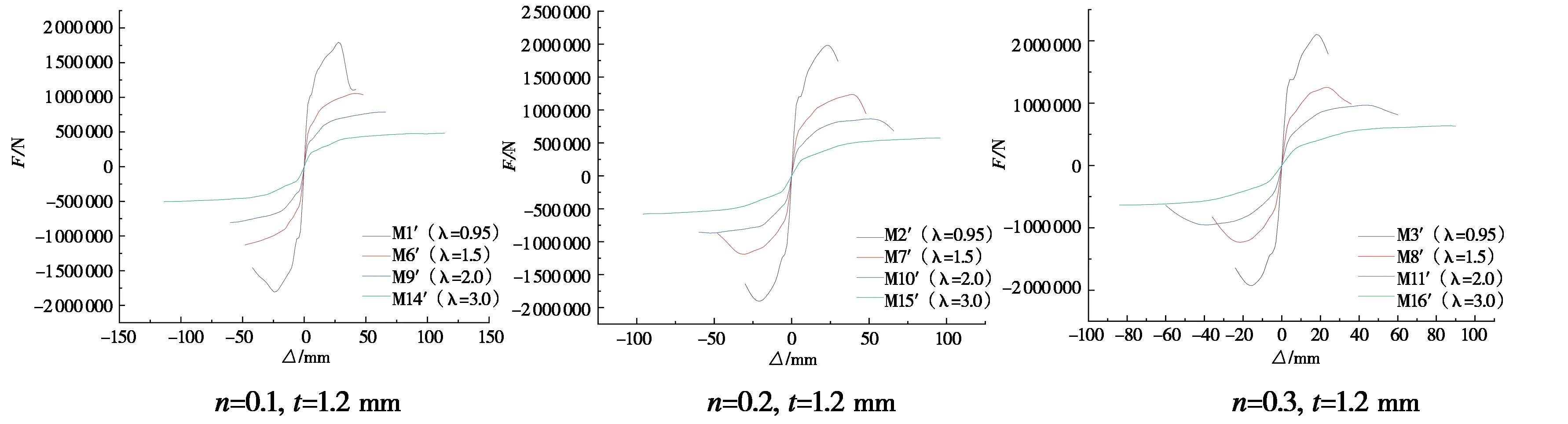
图7 不同剪跨比条件下M型型钢装配式钢筋混凝土剪力墙骨架曲线图Fig.7 Skeleton curves of M-shaped steel fabricated reinforced concrete composite shear wall with different shear span ratios
4.2 轴压比参数变化结果分析
本文以3组不同剪跨比作为一定条件,每组取3个不同轴压比作为变量(0.1、0.2、0.3)。相比轴压比为0.1的模型MSSCW1′、MSSCW6′、 MSSCW9′,轴压比为0.2的模型MSSCW2′、MSSCW7′、MSSCW10′水平峰值荷载分别提高了13.14%、15.09%、8.86%;相比轴压比为0.2的模型MSSCW2′、MSSCW7′、MSSCW10′,轴压比为0.3的模型MSSCW3′、MSSCW8′、MSSCW11′水平峰值荷载分别提高了6.06%、7.46%、3.63%。通过数据的对比分析发现,随着轴压比增大,水平承载力会依次增加,屈服位移及极限位移会随之减小,位移延性系数会随着轴压比的增加逐渐降低。M型型钢装配式钢筋混凝土剪力墙在不同轴压比条件下的骨架曲线如图8所示。
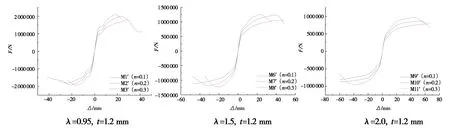
图8 不同轴压比条件下M型型钢装配式钢筋混凝土剪力墙骨架曲线图Fig.8 Skeleton curves of M-shaped steel fabricated reinforced concrete shear wall with different axial compression ratios
4.3 型钢厚度参数变化结果分析
本研究在n=0.1,λ=0.95;n=0.2,λ=2.0;n=0.1,λ=2.0的条件下,通过改变型钢厚度(1.2、2.4、3.6 mm)分析其对剪力墙抗剪承载力的影响。相对于模型MSSCW1′、MSSCW9′、MSSCW10′(t=1.2 mm),模型MSSCW4′、 MSSCW12′、MSSCW17′(t=2.4 mm)水平峰值荷载分别提升了1.14%、2.33%、2.53%,模型MSSCW5′、 MSSCW13′、MSSCW18′(t=3.6 mm)水平峰值荷载分别提升了2.29%、5.81%、5.06%。通过分析发现,改变型钢的厚度对于剪力墙水平承载力的改善并不大,但随着型钢厚度的增加,位移延性系数会随之增加;剪跨比越大,位移延性系数增加的幅度则越大,进一步说明型钢在中、高剪力墙中更能发挥其抗拉性能,与剪力墙共同承担水平承载力。M型型钢装配式钢筋混凝土剪力墙在不同型钢厚度条件下的骨架曲线如图9所示。
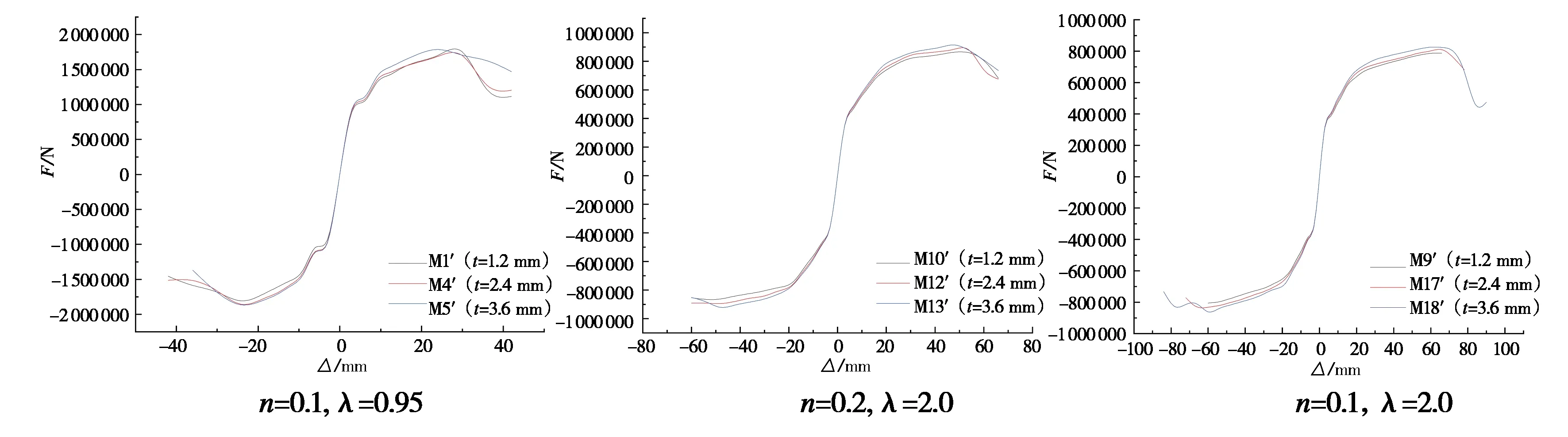
图9 不同型钢厚度条件下M型型钢装配式钢筋混凝土剪力墙骨架曲线图Fig.9 Skeleton curves of M-shaped steel fabricated reinforced concrete shear wall with different thicknesses
通过18组数据的综合对比发现,M型型钢装配式钢筋混凝土剪力墙中的型钢在剪力墙剪跨比为2.0时其延性系数达到峰值,出现了最适剪跨比;在剪力墙轴压比为0.2时,剪力墙承载力及延性系数达到最佳。基于此模拟结果分析,建议在实际工程中将M型型钢多应用于剪跨比为2.0,轴压比为0.2的剪力墙中,相信更能发挥其在地震中的耗能能力。
5 讨论与结论
本文基于MSC MARC有限元软件对M型型钢装配式钢筋混凝土剪力墙进行模拟,通过有限元模拟结果与试验结果的对比验证发现,二者的滞回曲线及骨架曲线趋向规律基本一致,峰值荷载及峰值位移基本相同,这说明本文建立的有限元模型可以有效模拟试验中试件的受力性能。以此模型为基础,改变试件参数作进一步模拟分析,得到结论如下:(1)在轴压比一定的条件下,剪跨比越大,抗侧刚度则越小,水平承载力也随之减小;当剪跨比未超过2.0时,位移延性系数随剪跨比增大而增加,当剪跨比超过2.0时,位移延性系数开始减小。因此,在适当范围内提高剪跨比,对整体耗能能力有利。(2)随着轴压比的增大,剪力墙的水平承载力逐渐增加,屈服位移及极限位移随之减小,位移延性系数随着轴压比的增加逐渐降低,当其达到峰值荷载之后,轴压比越大,刚度退化越快,且变形能力越差。但随着轴压比增大,水平承载力增加的幅度却不断下降,这表明对于剪力墙墙体,需要在合理范围内提高轴压比,这样不仅能提高其抗剪承载力,还能保证其耗能能力。(3)相比较小剪跨比(λ=0.95,λ=1.5)的剪力墙,大剪跨比(λ=2.0,λ=3.0)的剪力墙随着型钢厚度的增加,位移延性系数增加的幅度较大。
本文所研究的M型型钢装配式钢筋混凝土剪力墙相比较程小卫等[15]研究的普通钢筋混凝土剪力墙而言,延性较好,在高层建筑结构抗震中其耗能能力较强。但由于在有限元模拟中很难模拟出型钢与混凝土之间的粘结滑移现象,因此和试验结果存在少许误差,对此需做进一步研究。

