基于Floyd算法和线性规划的疫情防控物资配送方案
惠庆华,张恒运,唐晨洋,杨梦瑶,朱冠霖,胡修志,吴玉帅*
(1.青海省测试计算中心有限公司,青海 西宁 810001; 2.青海大学土木工程学院,青海 西宁 810016;3.青海大学水利电力学院,青海 西宁 810016; 4.青海大学生态环境工程学院,青海 西宁 810016;5.青海大学财经学院,青海 西宁 810016)
2020年初新型冠状病毒肺炎(COVID-19)的爆发给我国的物流行业带来了很大影响[1]。疫情防控期间,防控物资运输需求明显增加,特别是疫情严重地区对防控物资的需求在短时间内大幅增加,解决防控物资的合理调配问题显得至关重要。保障运输过程中经济与速度之间的平衡,就是在最短运输路径和最低成本之间找到一个合理的运输方案[2]。目前,关于配送最优方案的研究较为广泛,胡小宇等[3]利用粒子群算法求得了单仓储多车物流的配送问题,并且设计了全新的粒子更新方法,并验证了该算法的有效性;周显春等[4]针对现实的交通状况,构建了基于不同约束条件的最优路径评价模型;刘海洋等[5]在研究分析公交车道设置的基础上,提出基于 Floyd 算法城市最短路径的规划,有效解决公交车道的最优路径。因为绝大多数最短路径规划不仅仅局限于路径规划,还引申至其他度量,所以使用最频繁的算法仍然是Floyd 算法[6]。当前主要的最优距离求解均为改进的最优解距离算法,而没有将不同的算法进行结合[7]。鉴于此,本文通过Floyd算法和线性规划相结合的方式,以供给点到需求点的最短供给时间、最大运输量为目标,使运输路径和运输成本之间保持平衡,得到疫情防控物资配送的最佳运输方案。
1 问题背景
某市(详情见图1)由于疫情爆发导致医疗物资及生活物资匮乏,为更好地解决问题,某市政府有关部门希望建立数学模型,为突发情况对医疗物资及生活物资的配送问题提供合理的运输方案。

图1 某市地形简图Fig.1 Topographic map of a city
图1中各边表示连接各县市的公路,各边的权值表示车辆通过该路段所需的时间。现已知丁1、丁2、丁33个地区爆发疫情,每天所需要的防控物资量分别为60、40、25 t。能够提供物资的地区有甲1~甲12,每天能提供物资的量分别为18、16、15、15、14、16、22、20、22、14、22、35 t,各供给地区提供物资的成本分别为3、2、4、3、2、4、2、3、5、3、4、4万元/t,在保证丁1、丁2、丁3每天物资供给充足的情况下,设计一种经济快速的物资运输方案。
通过分布图利用Floyd算法求解12个支援城市到3个疫情爆发区的最短时间,另外,通过确定权重,对经济配送和时间配送之间可能存在的制约进行分析,并建立综合评价经济效益和时间效益的风险度模型,通过遍历法求解权重,将建立的评价模型所得的函数作为线性规划的目标函数,得到最经济、快速的物资配送方案。
2 模型建立与求解
2.1 Floyd算法求解最短距离
Floyd算法(弗洛伊德算法)是解决两点间最短路径的一种算法,可正确处理无向图或有向图的最短路径问题,该算法又称插点法。它是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法[8]。此算法三重循环结构紧凑,简单有效,适用于多源最短路径 (All Pairs Shortest Paths,APSP),对于稠密图效果最佳,边权可正可负[9],效率要高于执行|V|次Dijkstra算法,也高于执行|V|次SPFA算法。因此,在综合考虑多种图论算法的情况下选择,Floyd算法对甲1~甲12到丁1~丁3之间的最短距离进行求解。在本研究中,每条边的权为一个地点到另一个地点的时间,可将图1进行标号处理,得到以下结果(图2)。
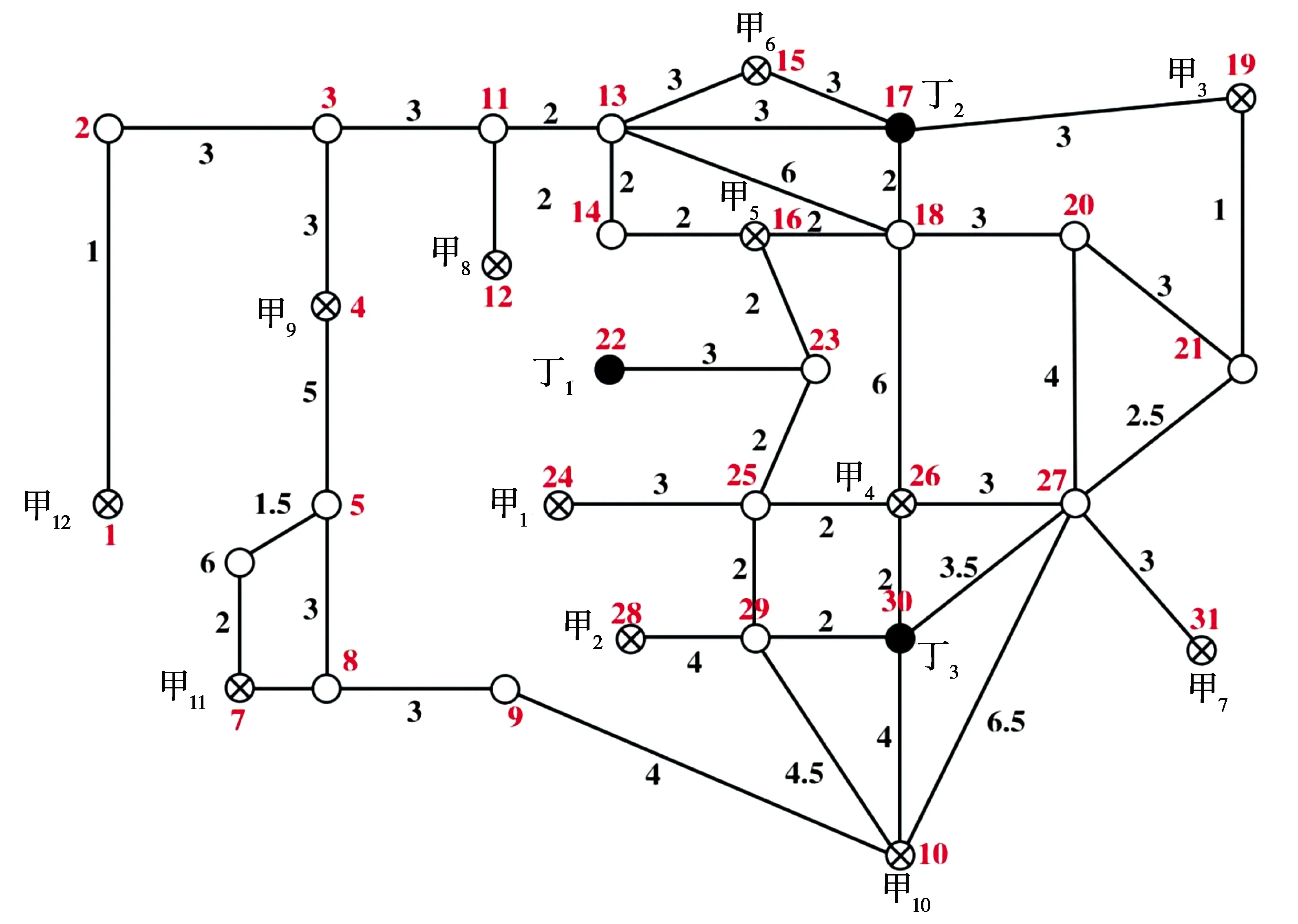
图2 标记顺序后的某市地图Fig.2 Map of a city after marking sequence
G为邻接矩阵,G(i,j)元素是顶点i到点j之间的边权,可以是有向的,如果两点之间没有边相连,则权重为无穷大。对于每一项顶点i和j,是否存在一个顶点k,使得从i到k再到j比已知的路径更短,如式(1):
G[i][j]=min(G[i][j],G[i][k]+G[k][j])
(1)
如果G[i][j]的值变小,重新定义一个矩阵D用来记录所插入点的信息,如式(2):
D[i][j]=k
(2)
下表是根据Floyd算法计算出来的甲1~甲12到丁1~丁3的最短距离。

表1 疫情区防控物资供应最短距离Tab.1 Shortest distance of epidemic prevention materials supply in epidemic area
对最短距离进行求解,得到36个结果,为了方便后续计算,这里将其列为1行36列的矩阵t,如式(3):
t=[t1,t2,t3…t36]
(3)
式中:[t1,t2,t3…t12]代表甲1~甲12中每个地区到丁1的最短时间(最短距离),[t13,t14,t15…t24]代表甲1~甲12中每个地区到丁2的最短时间,[t25,t26,t27…t36]代表甲1~甲12中每个地区到丁3的最短时间。
2.2 多目标和线性规划模型的建立与求解
本文的目标是从可提供物资的县市(甲1~甲12)向3个疫情爆发区(丁1~丁3)进行支援时,得到一个经济快速的防控物资运输方案。对于运输过程而言,运输的风险与单向运输的成本和运输到达区域最短时间有关,且二者可能存在一定的相互制约现象。因此,本文建立相应的线性规划模型来分析运输风险,如式(4):
R=Rtotal+Rtime
(4)
式中:R为整个运输过程中的风险,Rtotal为运输物资量的风险,Rtime为运输到达区域最短时间的风险。
每个提供物资的区域可提供的最大值恒定,且提供物资的数量不会影响到达不同地区的时间,即提供物资的数量和到达时间相互独立。在抗疫期间,物资到达时间的早晚对疫情防控工作更为重要,而经济上的成本更容易随着政府的政策倾斜而被妥善解决,所以支援时间的权重更为关键,即支援时间的权重越大,就会产生更好的反响,反之会产生更大的风险。因此,本文将Rtime的权重设置为a(0≤a≤1),Rtotal的权重设置为b(0≤b≤1),从而得出以下线性规划风险度评价模型,如式(5):
(5)
将运输物资量的风险和到达区域最短时间的风险进行量化,运输物资量的风险主要为运输成本的风险。
这里设xi表示从i地区支援到丁1~丁3地区所需物资的数量,其中i表示甲位置,i=1,2,3…12。由于目的地分别为丁1、丁2、丁3,从i地区支援目的地共有3种情况:x(1,i)=(x1,x2,x3…x12),代表甲1~甲12中每个地区到丁1的物资供给量;x(1,i+12)=(x13,x14,x15…x24),代表甲1~甲12中每个地区到丁2的物资供给量;x(1,i+24)=(x25,x26,x27…x36),代表甲1~甲12中每个地区到丁3的物资供给量。
成本风险以运输成本表示,则为运输吨数与每吨成本之积,即式(6):
Rtotal=[x(1,i)+x(1,i+12)+x(1,i+24)]m(i)
(6)
式中:m(i)为每吨运输成本。
此外,将到达区域最短时间的风险量化为该时间下的运输量总量。在保证经济的情况下,为了尽快到达支援目的地应既要保证尽快运送,又要保证运送的量合适,达到经济效益的最大化,见式(7):
Rtime=xit
(7)
其中:t为运输时间。
在考虑风险度的情况下,由于本文着重考虑Rtime带来的影响,认为Rtime的增加和减少会带来更多的客观影响,并没有着重考虑二者之间的制约;但是考虑在实际运输过程中,Rtime和Rtotal之间存在着相互制约,且运输方案更偏向于经济和速度的平衡,因此在通过风险度求解权重的情况下,建立线性运输模式代价模型,如式(8):
C=bRtotal+a2Rtime
(8)
式中:C代表不同运输方式所需的代价。
基于丁1~丁3每天所需的物资及甲1~甲12可运送的有限最大物资量,建立相应的边界条件,对物资运输进行线性规划。
丁1~丁3每天所需的物资量约束条件如式(9):
(9)
甲1~甲12可运输的最大物资量的约束条件如式(10):
(10)
3 结果与分析
通过建立线性规划风险度评价模型,对权重a、b进行遍历选取,从而得到风险最低的权重。通过Matlab R2017对b权重以0.01的步长进行遍历分析,得到各个权重下的所有风险度值,再通过origin将风险度值进行可视化(图3),从而得到步长为0.01权重,b在0~1范围内的所有风险度数值。当权重b为0.81时,风险度298.2为最小风险值,由式(5)可得到此时权重a为0.19。因此,在考虑风险度的过程中,权重a=0.19,b=0.81时所得到的风险值最低,然后将风险度最低的权重代入求解不同分配模式的代价模型,得到线性规划的目标函数为:
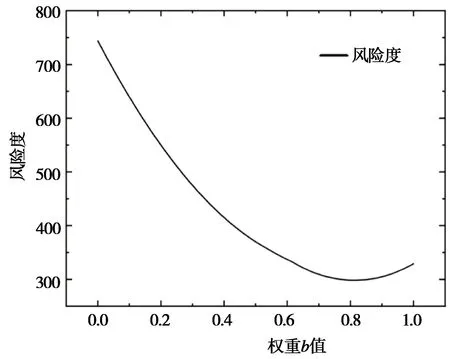
图3 权重风险度可视化图像Fig.3 Visualization image of weight risk
C=0.81Rtotal+0.192Rtime
(11)
在风险度最低为298.2的情况下,将该风险下的权重代入运输模式代价模型,得到疫情防控物资运输分配结果(表2)。

表2 防控物资运输分配结果Tab.2 Distribution scheme of epidemic prevention materials
由表2可知,甲1向丁1运输18 t物资;甲2向丁1运输16 t物资;甲3向丁2运输6 t物资;甲4向丁1运输12 t物资,向丁3运输3 t物资;甲5向丁1运输14 t物资;甲6不运输;甲7向丁2运输14 t物资,向丁3运输8 t物资;甲8向丁2运输20 t物资;甲10向丁3运输14 t物资;甲9、甲11和甲12不进行运输的模式,能达到经济快速地运输防控物资的目的。
4 讨论与结论
本文通过Floyd算法和线性规划模型的结合,引入运输模式代价的理念寻找相应的权重,得到了风险度最低值及相应的分配模式。采用以K-means算法为主的“聚类算法”进行物资调配[10]时,不能分析调配物资量与风险度之间的关系;传统的优化算法[11]进行物资调配策略运行时,需要在事件爆发的瞬间就做好应急处理,对从未接触过的突发状况而言存在很大的漏洞。而本研究的模型简单、易搭建,可快速进行最短路径规划。
本研究得出,当运输时间的权重为0.19,运输总量的权重为0.81时,可得到最低风险度数值298.2,运输方案为甲1向丁1运输18 t物资;甲2向丁1运输16 t物资;甲3向丁2运输6 t物资;甲4向丁1运输12 t物资,向丁3运输3 t物资;甲5向丁1运输14 t物资;甲6不运输;甲7向丁2运输14 t物资,向丁3运输8 t物资;甲8向丁2运输20 t物资;甲10向丁3运输14 t物资,甲11和甲12不进行运输。可见,在多种情况下,如果要保证时间和成本平衡,并不代表对需要支援的城市均给予相应的援助,最好的方案是“就近支援”,即每个城市支援最近的区域,就能保障运输成本与速度。同时,本模型也存在着不足,没有考虑到在运输途中可能出现的意外事件等小概率问题,只考虑了运输时间和运输成本两个因素来分析风险度,导致模型并不完善。此外,对“经济快速”的定义只限于成本和时间这两个因素,没有考虑其他因素,导致分析的结果趋于单一化。因此,得出的结果仍然需要全方位改进。

