基于拉索受力的车辐拱稳定性分析★
成 乐,陈 航
(1.北京交通大学土木建筑工程学院,北京 100044;2.长江科学院 水利部岩土力学与工程重点实验室,湖北 武汉 430010)
1 概述
车辐拱的稳定性一直是车辐拱研究中的重点问题。目前钢拱的稳定研究已经相当成熟,而车辐拱由于拉索对主拱结构有牵制作用,其稳定问题更为复杂。郭彦林等[1-4]针对车辐拱结构进行了一系列研究,包括车辐拱的弹性稳定,例如车辐拱的初始缺陷敏感性、结构参数以及荷载形式对弹性极限承载力的影响等。在弹塑性稳定方面,王高宁[5]分别总结了圆弧形、椭圆形、抛物线形和悬链线形车辐拱的失稳模态和受力特点,给出了稳定承载力随矢跨比和索盘高度的变化曲线。总的来说,目前对车辐拱弹塑性稳定性能的研究相对较少,且现有研究仅限于对结构整体进行的一些定性研究,鲜有学者从拉索受力的角度出发,考察其在车辐拱结构受力过程中起到的作用,关于这方面的研究内容仍有待补充。
针对以上问题,采用有限元数值方法进一步研究车辐拱弹塑性稳定特点;研究受力全过程中拉索的受力变化及车辐拱稳定承载力的影响,考察用撑杆代替拉索的新型车辐拱的结构性能特点。
2 有限元模型
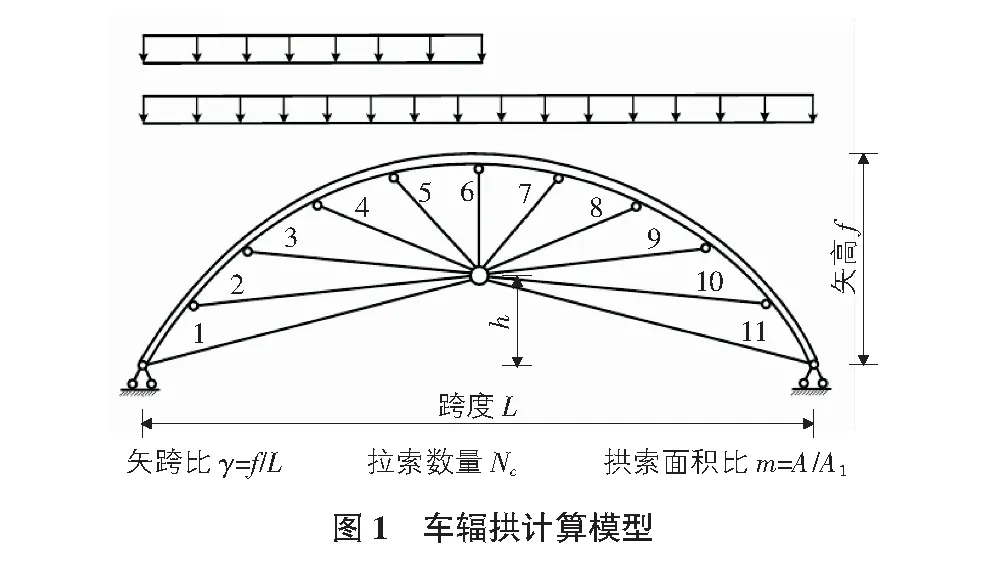
图1为两铰圆弧形车辐拱的计算模型,其中,f为拱的矢高;h为索盘高度即索盘中心到拱脚连线的垂直距离;L为结构的跨度。拱体截面面积为A,A1表示单根拉索截面面积。定义主要结构参数矢跨比γ、拉索数量Nc、拱索面积比m。跨度L=50 m,Nc=11,m=10,索盘高度h按照JGJ/T 249—2011拱形钢结构技术规程[6]中的建议取0.5f。拱体采用工字形截面800 mm×400 mm×10 mm×16 mm。
采用有限元软件ANSYS[7-8]中直接建单元的方法创建有限元模型,主拱采用Beam188单元,拉索采用Link180只拉不压单元。以纯拱的一阶反对称屈曲模态为初始缺陷的分布模态,其缺陷峰值取L/1 000。钢拱采用双折线弹塑性材料本构,弹性模量E=2.06×105MPa,切线模量Et=0.01E。拉索采用平行钢丝束,假定为线弹性材料,弹性模量Ec=1.95×105MPa,不考虑拉索预应力。如无特殊说明,拱体钢材屈服强度取fy=390 MPa。
3 稳定性能
基于有限元软件ANSYS进行车辐拱在全跨和半跨竖向均布荷载作用下的面内弹塑性稳定分析。
3.1 应力及变形
图2,图3分别给出了车辐拱在半跨和全跨均布荷载作用下失稳时的变形和应力分布情况,为方便观察将拉索截面放大10倍,将变形放大5倍并和相同条件下的纯拱变形作对比。变形为相对值(定义纯拱最大值为1),应力为实际值。
半跨荷载作用下,纯拱发生反对称变形,加载半跨发生向下的位移,而非加载跨发生向上的变形。同纯拱一样,车辐拱的变形也具有明显的不对称性,不同的是由于拉索的作用,主拱的位移有明显的减小,尤其是在靠近拱脚的位置。在受力过程中,车辐拱索盘有往右上方移动的趋势,故左侧第一根拉索达到了最大拉应力,而变形最大位置的几根拉索受主拱变形影响已经松弛,不能发挥作用。结合应力图和变形图可以看出,应力和变形是密切相关的,变形较大的地方,主拱应力也很大,相应位置的拉索基本已经松弛,而应力较小的地方拉索发挥的作用比较大。


全跨荷载作用下,结构达到极限承载力时,变形和应力基本保持对称。受反对称初始缺陷影响,纯拱结构右侧的变形要明显大于左侧,车辐拱结构也有类似的变形规律。受力过程中,车辐拱索盘有明显的向下移动的趋势,同时有微小的向右的侧移。从拉索的应力图可以看出,车辐拱中间位置的三根拉索和连接右侧拱脚的拉索已经松弛,不能发挥作用。故在这些位置主拱的应力较大。
3.2 拉索受力
以拉索为研究对象,通过绘制全过程荷载-索力曲线研究其在结构整个受力过程中的主要作用及受力情况,拉索编号见图1。
取车辐拱矢跨比为0.3时的典型荷载-索力曲线,观察各拉索在加载全过程的索力变化(见图4)。由于拉索数量较多,为便于观察,只绘制加载过程中受力的拉索。半跨荷载下编号为3,4,5,6的拉索全过程不参与受力,全跨荷载下编号为5,6,7,11的拉索全过程不受力(编号位置见图1)。

半跨荷载作用下,受力拉索在加载全过程中均表现出随着荷载的增大索力不断增大的特点。其中,连接左侧拱脚和索盘的拉索1始终索力最大,且变化幅度最大,而连接右侧拱脚和索盘的拉索11起初是松弛的,随着索盘位置的变化,才逐渐产生索力。总体来看拉索受力并不均匀,变形越小的位置拉索起到的作用越大。
全跨荷载作用下,拉索受力具有明显的对称性,中间位置的拉索5,6,7始终不受力,与之相邻的拉索4和8虽然参与受力,但索力很小,连接拱脚的1号拉索和11号拉索作用也不大。对称的3,9和2,10号拉索从加载开始一直就保持着较大的索力,荷载达到220 kN左右时,3和9号拉索索力开始下降,与此同时拉索2和10的索力快速增长,达到最大索力,各个受力拉索相互协调作用以控制结构变形。
表1全面总结了各个矢跨比下的拉索的受力情况,提取出了全过程不受力的拉索编号以及在达到极限承载力时索力最大的拉索编号。
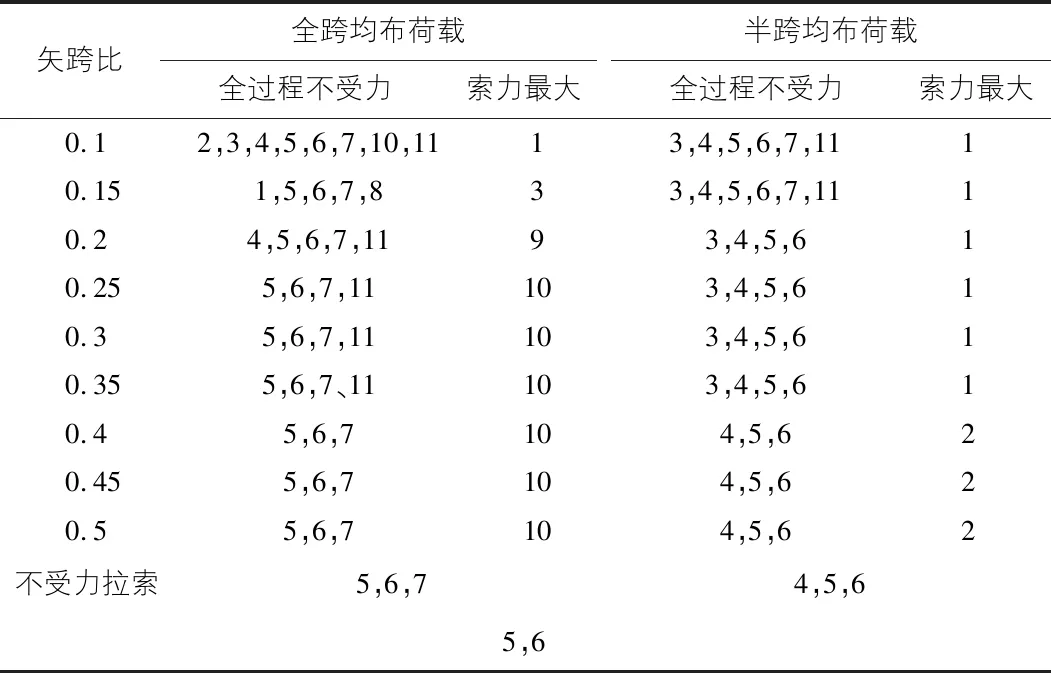
表1 拉索受力情况统计表
不难看出,在全跨和半跨荷载作用下,随着矢跨比的增大,全过程不受力拉索的数量在减少,也就是说矢跨比越大参与受力的拉索越多,这是因为矢跨比越大主拱的变形越大,进而需要更多的拉索来限制变形。另外,位移较大的位置拉索松弛不受力,索力最大的拉索连接处拱的位移很小,这和3.1中关于应力与变形的分析结论相一致。
4 优化设计
4.1 优化方法
从3.2可以看出,车辐拱中总是存在着全过程不受力的拉索,这是由于这些拉索受主拱变形的影响处于松弛的状态,已经松弛的拉索不能充分发挥作用,但是也不能取消,因为这些拉索在风吸力作用下是可用的。为了使各拉索之间受力更加均匀、每根拉索都能发挥其作用,本节提出用可承受轴向拉压的撑杆来代替全过程不受力的拉索的一种新型车辐结构。
考虑表1中全过程不受力拉索以及结构的对称性,采用以下几种构型的新型车辐结构(如图5所示,CF-57表示第5号和第7号拉索用撑杆替代)进行相关研究。采用Link180单元模拟撑杆,用KEYOPT(3)设置轴向拉压。撑杆截面面积取主拱截面面积的1/10,弹性模量取1.95×105MPa。

4.2 优化结果
用ANSYS对上述几种新型车辐拱进行弹塑性稳定分析,对比原车辐拱结构,从极限承载力、荷载-位移曲线、拉索索力变化和拱脚推力这四个方面探讨新型车辐拱的受力性能。
4.2.1 极限承载力
从图6的极限承载力对比可以看出,在半跨荷载下,新型车辐结构的承载力较原车辐拱都有所提高,CF-6提高幅度较小,在矢跨比为0.1时达到最大提高率10%,CF-57和CF-567的矢跨比-承载力曲线完全重合,均表现出随着矢跨比增大承载力提高率先增大后减小的变化趋势,在矢跨比为0.3时,承载力提高率可以达到60%。

全跨荷载下则呈现出截然不同的变化规律,CF-6,CF-57,CF-567三种车辐拱承载力相差不大,在矢跨比较小时CF-57和CF-567的承载力微高于CF-6,随着矢跨比的增加,三种新型车辐结构的承载力增长率逐渐减小,矢跨比为0.1时,增加撑杆可以将承载力提高10%左右,而当矢跨比大于0.3后,新型车辐结构的矢跨比-弹塑性极限承载力曲线和原车辐结构完全重合。总体来看,全跨荷载下,用撑杆代替不受力拉索的构型方法对提高车辐拱承载力的作用不大。
4.2.2 荷载-位移曲线
图7给出了几种车辐结构在矢跨比为0.3时的荷载-位移曲线,半跨荷载下提取1/4跨处的竖向位移,全跨荷载下取跨中竖向位移。
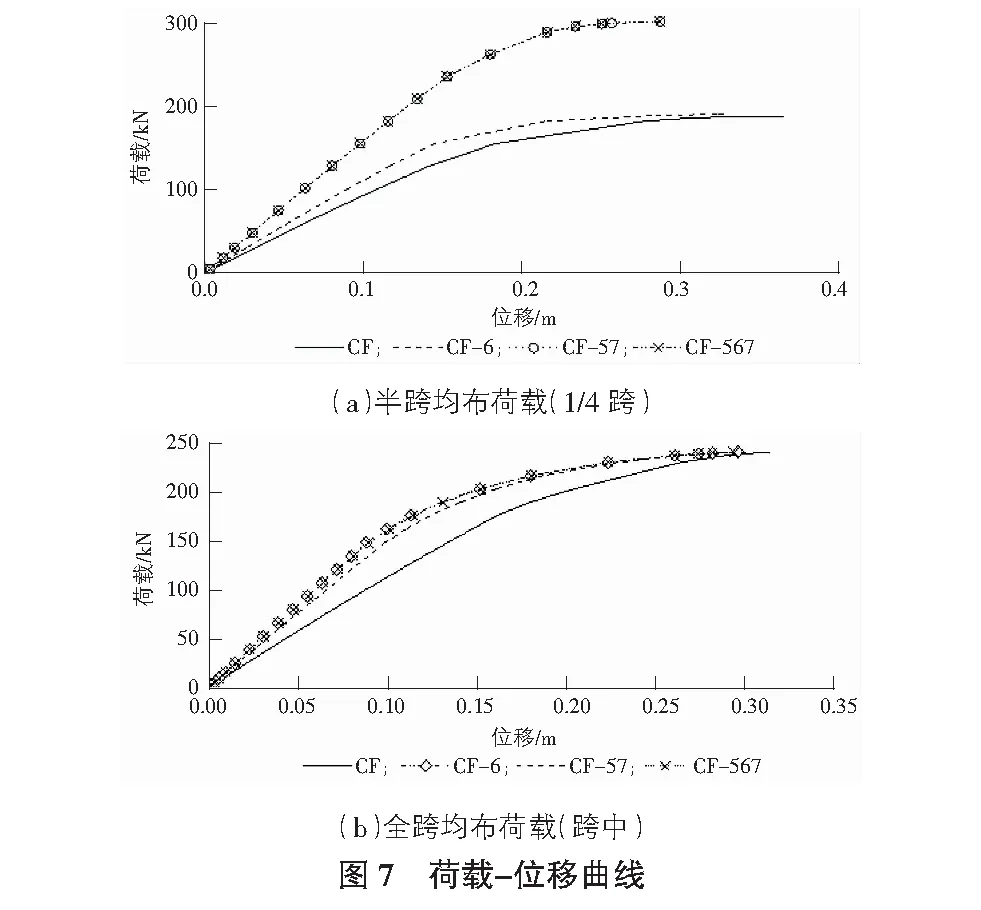
不难看出,在全跨和半跨荷载下,CF-6,CF-57,CF-567的结构刚度较原车辐拱均有明显的增大,这种增大作用在半跨荷载下尤为明显,CF-57和CF-567的荷载-位移曲线总是保持一致,CF-6的刚度介于CF-57,CF-567和CF之间。
从达到极限承载力时的位移大小来看,半跨荷载下撑杆的存在不仅能有效提高结构承载力还能减小结构位移。而全跨荷载下撑杆的存在只是改变了位移的变化路径并没有改变结构达到极限承载力时位移的大小。
4.2.3 拉索索力
为更加全面地了解撑杆的存在对车辐拱受力的影响,考察矢跨比为0.3时,不同结构形式下同一位置拉索达到极限承载力时的索力值,绘制如图8所示的索力变化曲线。

半跨荷载作用下,多数拉索的内力值都有很明显的变化。CF-6中撑杆6承受了轴向压力,压杆6附近的拉索7索力有所增加,与此同时其他位置拉索索力均有所下降,承受最大索力的拉索1的索力值下降尤为明显,降幅高达52%,这有利于降低索力分布的不均匀性;CF-57和CF-567的各杆件内力并无差异,撑杆5承受了轴向压力,拉索1的索力较CF基本没有变化,受力为零的拉索3,4仍保持为零,拉索2,6,7,8,9的索力都有所增加,拉索10和11则由原本的受力变成不受力。
全跨荷载下,拉索的内力值基本不受撑杆影响,只有5,6,7三个位置的杆件存在轴力变化且变化值很小。这也很好的解释了为什么全跨荷载下结构极限承载力和位移基本保持不变。
4.2.4 拱脚推力
拱形钢结构在竖向荷载作用下会产生较大的拱脚推力,拱脚推力越大,对拱脚构造的要求就会越高,所以拱脚推力一直都是设计中比较关心的问题[9]。本节考虑各个矢跨比下的拱脚推力计算值,以相同条件下纯拱(CG)的拱脚推力为基准值,计算车辐拱的拱脚推力变化率,结果如表2所示。
从表2的数值可以看出,任意荷载工况下,相对于纯拱而言,车辐拱的拱脚推力均有所降低,且降幅均随着矢跨比的增大而迅速增大。矢跨比相同时,半跨荷载下的拱脚推力降幅要高于全跨荷载。全跨荷载下,新型车辐拱结构的拱脚推力和原车辐拱结构相差不大,半跨荷载下,新型车辐拱结构拱脚推力要略高于原车辐拱结构。总的来说,把拉索换成撑杆对车辐拱拱脚推力影响不大。
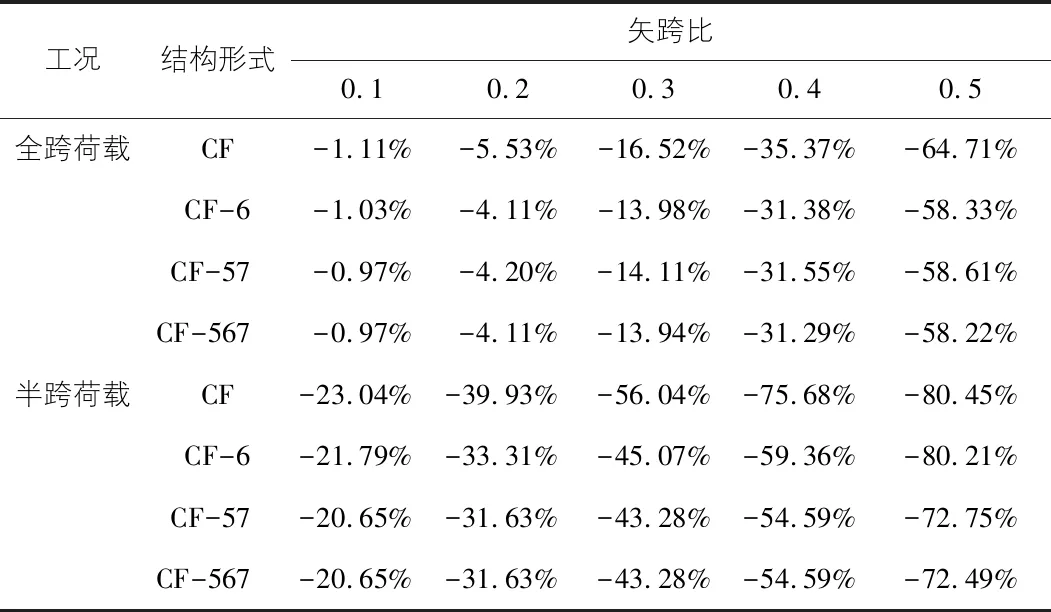
表2 拱脚推力变化率
5 结语
本文以两端铰接圆弧形车辐拱结构为研究对象,考察其在全跨和半跨均布荷载作用下的面内弹塑性稳定性能,提出了一种以撑杆代替拉索的新型车辐拱结构并对其进行了受力分析。主要结论如下:
1)从车辐拱的应力和变形图来看,应力和变形是密切相关的。在主拱变形较大的位置,应力也很大,相应位置的拉索基本已经松弛,故拉索应力很小;相反,在主拱应力较小的地方,拉索发挥的作用比较大,对应的拉索应力也很大。
2)车辐拱中总是存在着全过程不受力的拉索,不受力拉索的数量随着矢跨比的增大而减少。
3)用撑杆代替全过程不受力拉索提出的新型车辐拱结构对改善全跨荷载作用下车辐拱的受力作用不大。而在半跨荷载下,撑杆的存在能大幅度提高结构的极限承载力,也能调整拉索受力、有效降低极限索力、增大结构刚度,与此同时结构的拱脚推力略有增加,但增长幅度不大,基本不超过20%。