地震灾害下-电 气综合能源系统的韧性评估

尹昊冉,崇振霄,郝金慧,赵 宇,杨丽君

(1.国网安徽省电力有限公司歙县供电公司,安徽 黄山 245200;2.河北省电力电子节能与传动控制重点实验室(燕山大学),河北 秦皇岛 066004;3.中核四〇四有限公司,甘肃 兰州 732850)

0 引言

近年来频繁发生的海啸、地震、风暴、台风等极端灾害引发了许多大规模的能源供应事故,造成巨大的经济损失和社会影响[1]。在各种极端灾害中,因为海啸和地震具有难以预测且发生快速的特点[2],导致系统供能设备出现难以估计的破坏。与极端灾害密切相关的一个重要评估概念是韧性(Resilience),用以表达系统在极端灾害事件中所承受的压力和恢复到原有状态的能力[3]。

当前,人们对传统电力系统韧性已有了较深入的研究,在韧性评估指标研究方面:文献[4]从物理、网络、人文的角度建立了城市电力系统恢复力的多准则评估框架,确定了15个评价指标;文献[5]指出关键部件识别是提高电网对灾害恢复能力的重要问题,并提出一种面向恢复力的电力系统关键部件识别方法。在量化指标方面:文献[6]利用台风灾害时配电网各时间阶段数据,对台风灾害下配电网系统全过程的恢复供电能力进行评估。文献[7]引入了韧性等级的概念根据连续攻击下产生系统中断所需的最小故障数来评估电力系统的恢复能力,并通过深度强化学习的方法来确定韧性等级;在综合能源系统方面,文献[8]通过区分地质灾害和地表灾害确定电-气耦合系统组件的破损程度和运行状态,利用马尔可夫状态转移方程计算出韧性指标;文献[9]从鲁棒性、快速性、冗余性的角度求解并分析灾后供能恢复能力,勘察系统的薄弱环节并提出改进方案。综上所述,电-气综合能源系统韧性的定性定量分析及评价尚无一个确定的框架体系,确立合理有效的韧性评估指标以及有效的评估方法是迫切需要研究的课题。

本文对含配电网和区域天然气系统的电-气综合能源系统在地震情形下的韧性评估方法展开研究。首先,建立地震典型场景,利用马尔可夫状态法建立电气综合能源系统在不同等级地震下的状态转移模型。其次,构建应对地震灾害的电-气综合能源系统全时段多级韧性评估指标体系,给出地震灾害下电-气耦合系统的指标量化值。最后,采用基于博弈论的组合权重法确定系统各韧性指标的评估权重,并对不同地震灾害程度下的电-气综合能源系统的韧性进行评估校验,以由18节点天然气系统改进的IEEE30节点配电系统为例进行仿真,验证本评估方法的有效性。

1 地震灾害场景模型建立

1.1 典型灾害场景获取

目前灾害场景模拟的方法主要有基于灾害模型[10]和灾害数据模拟两大类。本文考虑地震灾害历史数据不足,结合上述2种模拟方法开展地震灾害模拟,以地震为例进行的灾害模拟典型故障场景获取过程如图1所示。

图1 地震灾害典型故障场景获取流程

采用蒙特卡洛方法和历史地震数据模拟地震灾害信息,在此基础上利用K-means聚类划分典型故障场景,获得地震灾害下系统的故障典型场景集。

1.2 基于马尔可夫状态的系统转移模型

马尔可夫链可有效表达恢复过程中电-气综合能源系统处于各种状态及状态之间的转移过程。依据系统的运行情况可定义四种运行状态:正常运行状态、以电定气状态、以气定电状态和故障状态。结合典型地震灾害场景集和马尔可夫状态模型,实现不同情形下四类系统状态的转移,三种马尔可夫状态转移模型如图2-4所示。

典型场景1为地震等级在4.5级以下时,电网恢复过程由正常运行状态Θ1和故障状态Θ2构成,转换过程见图2。

图2 地震等级4.5级以下的电-气耦合系统两状态模型

典型场景2为地震处于4.5到6级之间时,电-气综合能源系统恢复过程由正常运行状态Θ1、以电定气状态Θ2和故障状态Θ3构成三状态马尔可夫状态转移模型见图3。

图3 地震等级4.5～6级的电-气耦合系统三状态模型

典型场景3为地震处于6级以上时,构建由正常运行状态Θ1、以电定气状态Θ2、以气定电状态Θ3和故障状态Θ4构成如图4所示的四状态马尔可夫转移模型。

图4 地震等级6级以上的电-气耦合系统四状态模型

通过式(1)-(5)可计算三模态模型的状态概率向量N3=[Θ1,Θ2,Θ3]T和四模态模型的状态概率向量N4=[Θ1,Θ2,Θ3,Θ4]T。

式中:p ji为系统从状态Θj转移到Θi的概率;Θi为转移向量N n中的第i个转移向量,表征不同的系统运行状态;P i为第i个状态模型的状态转换矩阵;N n为第n个状态模型的状态概率向量。

2 电-气综合能源系统韧性恢复力指标体系和评估框架

2.1 韧性趋势

在极端事件发生后系统韧性曲线与系统的鲁棒性、适应性和各子系统耦合运行程度有关[11-13]。以三状态与四状态模型为例,两种状态模型对应的系统韧性趋势分别如图5所示。

图5 三、四状态模型的系统韧性变化趋势

在三状态模型中,天然气系统基本不受到破坏,仅电力系统受到破坏,其鲁棒性和适应性都表现在四状态模型中,电力系统和天然气系统均受到破坏。韧性曲线的横坐标主要分为以下时刻:t0为极端灾害发生时刻;t d为灾害导致系统降落到最大损失时刻;t d-t a为恢复阶段1,在此期间保证恢复全部关键负荷的基础上最大限度的恢复非重要负荷量;t a-t r为灾区能源负荷持续恢复供电阶段2,在此期间电力系统和天然气系统相互耦合能有效提升系统的供能恢复。韧性恢复曲线中各个时间区间对应于灾害事件灾害发生前、灾害发生后、恢复阶段1、恢复阶段2。

2.2 韧性指标体系定性评估

基于典型地震故障场景集合,针对韧性恢复曲线的不同时间阶段和系统属性,结合不同地震场景下设施元件故障概率需要确定并建立电-气综合能源系统韧性评价指标[14]。本文分别从时间阶段角度和系统指标等级考虑,建立电-气综合能源系统韧性评价指标体系如表1所示。

表1 电-气综合能源系统韧性评价指标体系

2.3 韧性指标体系量化分析

为了实现定量评估表达各指标对于韧性提升的贡献度,本文以马尔可夫状态模型为基础,分别给出各指标量化公式。

2.3.1 鲁棒性能力量化分析

反映电-气耦合系统鲁棒性能力的指标可以理解为综合能源系统的承受能力指标,其中包括:网络破损度、连通因子、供能效率比,并且以马尔可夫状态模型为基础,将求解得到的剩余负荷率也作为鲁棒性的指标之一。

(1)网络破损度

电-气综合能源系统网络在遭受地震后,系统会被破坏或遭到干扰导致网络结构分裂。可以利用在地震灾害后计算最大联通子图的节点数与原有节点数目之比

式中:Nmax为受到破坏后网络中最大联通子图中所包含的节点数;N os为原始网络的总节点数。

(2)联通因子

当电-气综合能源系统网络受到破坏时,会分成数个子网络,设网络受到破坏前系统网络的子图个数m与受破坏后网络破碎成m＇个子图的比值为联通因子τ

(3)供能效率比

供能效率是指电-气综合能源系统网络在一定条件下的整体供能效率,主要是利用供能节点和能量需求节点之间最短路径倒数的平均值作为系统供能效率。

式中:SG、SW、SD分别为发电机、气源、储气负荷节点集合;NG、NW、NS分别为发电机、气源、储气节点数;μp和μ0分别为系统破坏后的供能效率和系统破坏前的供能效率;e为供能效率比。

(4)剩余负荷比率

根据1.2节中三状态和四状态模型的概率向量可得出三状态模型的剩余电负荷比率以及四状态模型的剩余电、气负荷比率,并进行以下韧性指标量化。

2.3.2 快速性能力量化分析

本文将关键负荷恢复速度和修复速度作为初始恢复阶段和持续恢复阶段的快速性指标[13]。

(1)关键负荷恢复速度

根据负荷重要程度,可以分成:一、二、三级负荷。其中,一级负荷和部分重要的二级负荷称为关键负荷。极端灾害下的恢复时间表征系统对关键负荷恢复的快速性,其关键负荷恢复速度是指在各修复阶段单位时间的关键负荷供电恢复量。即时间段为t d-t a的关键负荷恢复速度。

(2)修复速率

修复速率为在极端灾害下由电力系统和天然气系统协调运行的系统恢复速度,即时间阶段为t a-t r的负荷恢复速度。

2.3.3 耦合能力量化分析

考虑到在电-气综合能源系统中的多能源的耦合性,引入α1、α2、α3、α4来表征耦合系统中各部分的不同重要程度,并提出ηele,ele、ηgas,ele、ηele,gas、ηgas,gas4个转换效率,分别表示在地震灾害下电能转换效率、气转电效率、电转气效率、燃气转换效率。三状态、四状态模型的值各不相同。其耦合性的参数公式如下所示

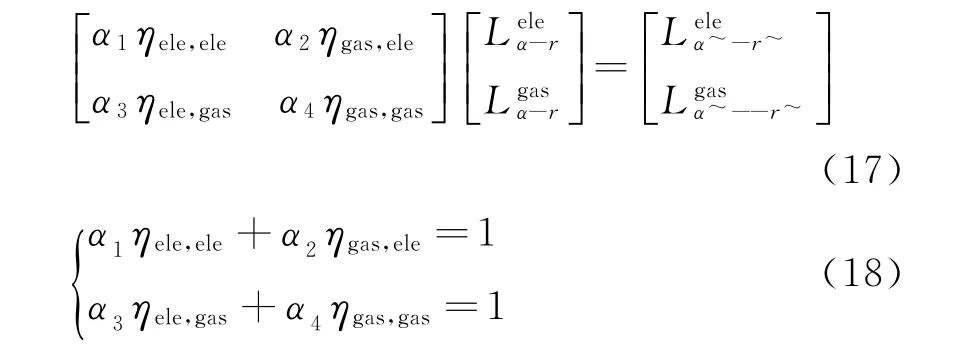
2.3.4 恢复程度量化分析

适应率ψad表示电-气综合能源系统经过修复过程后从性能最低点恢复到稳定运行状态的比例,其电力系统、天然气系统的适应率分别为

2.4 基于博弈论的组合权重综合评价方法

前述定义的韧性指标和韧性评价的方法存在多个参与若干韧性指标间复杂的映射关系,即1个参与主体贡献于多个韧性评价指标,而每个韧性指标又由多个参与主体共同评价。本文首先计算各参与主体对修复过程韧性指标的贡献度,对指标进行量化处理后,通过熵权法、层次分析法分别计算韧性评价指标的客观权重集、主观权重集,随后将各个韧性指标作为博弈的对象,利用基于博弈论的方法得出主观权重和客观权重比例σ、υ,经归一化的σ1、σ2满足式(21)-(23),最终通过式(24)计算出第i项指标的综合权重

式中:βi为第i项韧性指标的客观权重;αi为项韧性指标的主观权重;μi为第i项韧性指标的综合权重。

其次利用权重系数计算出各参与主体对修复过程二级指标的量化值。在此基础上利用定义各二级指标公式和二级指标权重分配系数进行二级韧性指标评估。最后通过一级权重分配系数和二级权重分配系数进行加权求和,分析电-气综合能源的韧性。

2.5 韧性静态评估

不同种类的马尔可夫状态模型下的韧性指标具有的差异性,本文结合综合能源系统的韧性指标量化和韧性曲线性能函数,在不同韧性恢复策略情形下使用基于博弈论的综合权重法确定系统各指标权重集合,最终采用以时间不变为前提条件的静态韧性综合评价方法。

(1)鲁棒性能力

鲁棒性能力是确定灾害对系统损害的程度,反应电-气综合能源系统承受能力的指标。一般来说,四状态模型是电-气综合能源系统受到冲击程度最大的,因此鲁棒性最差。综合能源系统的鲁棒性计算公式为

式中:ΔQ为电-气能源系统耦合运行时的鲁棒性能力;μ为各因素的影响权重;S为网络破损度;τ为连通因子;e为供能效率比;XALR为剩余负荷比率。

(2)快速性能力

电-气综合能源系统的快速性能力表征在系统恢复阶段t d-t r的恢复速度,恢复速度越快,系统越稳定,经济损失越小。根据不同地震场景集合下天然气系统和电力系统的协同运行程度差异,耦合性程度最大的四状态模型的恢复速度最快。结合各三级韧性指标的权重分配系数和耦合因子求和

式中:Δv为快速性能力;δ为系统对快速性的耦合影响因子;μ21为关键负荷恢复速度的综合权重;μ22为电力系统与天然气协同恢复的负荷速度综合权重;vre为负荷恢复速度;vrr为关键负荷恢复速度。

(3)恢复程度能力

电-气综合能源系统的恢复程度能力与耦合性因子有关,耦合性越强,恢复程度的提升越明显,因此四状态模型的恢复程度能力最强。

式中:Δψ为恢复能力;ξ为对恢复性指标的系统耦合影响因子;ψad为适应率。

(4)耦合性能力

将电-气综合能源系统分解为2个子系统:天然气系统和电力系统。两者通过能源集线装置进行协同运行以实现在以电定气和以气定电模式。四状态模型的三状态模型耦合性指标公式为

式中:Δρ为耦合性能力。

(5)综合韧性能力

通过以上四种指标能力值,利用二级权重分配系数加权求和,得到系统整体韧性值

式中:R为电-气能源系统耦合运行时的韧性综合评价能力;μn(n=1,2,3,4)为各一级指标分配的综合权重。

3 算例仿真

3.1 典型地震场景集

按图1所提出的地震灾害场景集合获取流程,得出3种聚类如图6所示,每种聚类分别对应系统遭受4.5级以下、4.5～6级之间和6级以上的地震后故障场景集合[15]。

图6 地震灾害场景生成

在不同等级的地震灾害场景下电-气综合能源系统的损坏程度分别为5%、20%、30%。

3.2 灾后综合能源系统韧性量化结果

本文引用文献[12]中部分数据,即采用由PV、WT、储能装置构成的18节点天然气系统所改进的IEEE30节点电力系统作为仿真算例,其系统的参数在不同模型下各不相同,具体见表2。

表2 各状态模型的电-气综合能源系统转换效率

(1)剩余负荷比率

将蒙特卡洛模拟方法得出的无故障工作时间和持续时间作为电-气综合能源系统遭受地震时的历史数据,以此计算λij和μij,结果如表3所示。

表3 地震情形下电-气综合能源系统的状态转移率

三状态和四状态模型的状态概率向量分别为

将各数据代入公式(10)-(12)分别求出四状态和三状态的剩余负荷比率值。在地震场景集2的三状态模型中,考虑到仅有电力系统受到较大的地震危害,因此天然气系统剩余负荷率为1,剩余电负荷率为0.665。在地震场景的四状态模型中,剩余气负荷率和剩余电负荷率分别为0.34、0.54。

(2)耦合性

鉴于系统的损坏程度低而且没有系统的恢复过程,二状态模型下的耦合性指标不予以考虑。取三状态和四状态模型的地震场景集合下电-气综合能源系统中的电力系统的耦合因子都为0.4,分别计算各场景的耦合性指标。

三状态模型下的天然气系统和电力系统耦合性指标分别为

四状态模型的天然气系统和电力系统耦合性指标分别为

(3)三级系统韧性指标量化结果

为确定剩余韧性指标的量化值,通过处理文献[12]和[16]中的数据,得到不同地震情景下的三级韧性指标的量化值。由于在地震场景1中的系统损坏程度低,故不考虑量化恢复阶段的韧性指标量,结果见表4、表5和表6。

表4 地震场景1的两状态韧性指标量化结果

表5 地震场景2的三状态韧性指标量化结果

表6 地震场景3的四状态韧性指标量化结果

根据上述数据,可计算出基于博弈论的三状态和四状态模型的综合评价权重集合,结果见表7。

表7 电-气耦合系统三级韧性指标权重集合

对指标进行归一化处理,结合子系统的量化值和子系统权重分配进行韧性指标加权求和,进而求解出三状态模型和四状态模型下电-气综合能源系统韧性指标量化结果,具体见表8。

表8 三状态模型和四状态模型电气耦合系统量化结果

3.3 基于博弈论的综合评价二级指标静态评估

基于以上条件,按照时间顺序进行两级指标三阶段的韧性评估,评估结果见表9。

表9 三状态四状态模型系统二级评估结果

由结果可知:同一地震场景集下电-气综合能源系统相比传统电力系统的鲁棒性稍有提升;三状态和四状态模型的电-气综合能源系统受地震灾害影响后,鲁棒性与系统损坏程度呈正相关关系,四状态模型比三状态模型电气耦合系统的鲁棒能力更差。

快速性体现在初始恢复阶段和持续恢复阶段中,电-气综合能源系统的快速性在耦合因子的作用下变高。在同一地震场景集中,电-气综合能源系统的快速性相比电力系统有一定程度的提升;四状态模型相比三状态模型电气耦合系统的快速性能力更强。

在耦合性方面,根据结果可知四状态模型相比三状态模型,电-气综合能源系统中子系统的耦合程度更紧密,因此协同运行效果更好、耦合性能力更强;在恢复程度方面,四状态模型相比三状态模型,电-气综合能源系统的恢复程度性能力更强。

3.4 基于博弈论的综合评价一级指标静态评估

利用一级权重向量加权求和计算出的一级韧性指标静态综合评估结果见表10。

地震灾害后的电-气综合能源系统显然具有更高的韧性,相比于电力系统,电-气综合能源系统的四状态模型的提升程度效果更强。综上所述,根据相关文献的实验结果,均表明本文一级韧性评估结果的可行性。在各二级韧性评估结果确定提升措施的基础上,一级韧性静态评估结果对选择最优的韧性提升措施具有重要意义。

4 结论

本文研究了电-气综合能源系统的韧性评估框架和方法。根据电-气综合能源系统韧性曲线图和系统遭遇风险后的恢复能力,建立了以时间顺序排列的电-气综合能源系统三级韧性指标体系;在对地震场景集仿真确定的3种集合的基础上,运用各地震场景集的转移模型和各公式指标分别对各韧性指标进行量化;通过静态综合评价步骤中的基于博弈论的层次分析法和熵权法确定权重集合,采用各级量化指标进行加权求和,得出静态韧性综合评价结果。相关研究内容验证了结果具有可行性。