基于一致性的综合能源微电网分布式优化调度

马 瑞,郝晓光,李剑锋,杨春来

(国网河北省电力有限公司电力科学研究院,河北 石家庄,050021)

0 引言

随着碳中和以及碳达峰的提出,可再生能源领域受到广泛关注,传统集中式架构大电网开始向去中心化的智能微电网转变,微电网中能源形式也朝着多元化发展。电力网络与互联网的深度融合使得电力能源的消费和利用正发生着重大变革[1]。随着电能与热能的综合利用,综合能源微电网的经济性调度成为当前亟待解决的问题(Econo mic Dispatch Problem,EDP)。近些年,关于微电网的EDP大多采用集中式方案来解决,该类方法虽然有效,但需要强大的中央控制器收集并处理大量数据,并且容错性能不够理想,出现单点故障时会导致系统不能正常运行且无法适应微电网灵活拓扑结构[2]。

为适应当下及未来的发展,新一代电力系统将集成通信控制和分布式控制。文献[2]提出一种基于分布式控制算法的孤岛微电网经济优化运行方法,在经济调度方面有一定研究。文献[3]提出一致和调整的方式实现分布式控制,一定程度上提高了控制精度。文献[4]提出一种基于离散一致性算法的智能多级控制策略,对交、直流微电网群的组网形式及群级协调控制进行了详细研究。文献[5]主要应用有领导者和无领导者2种方式实现微电网分布式控制。文献[6]设计了基于多智能体的微电网运行决策支持系统结构。以上所述的微电网分布式控制未发现考虑经济调度问题的综合能源微电网的相关论述,且对于一致性算法没有结合上位机进行整体实验实现。

本文基于一致性算法对综合能源微电网进行分布式优化调度研究,应用电力系统等成本微增率准则,确定综合能源微电网一致性变量,在考虑综合能源微电网功率平衡和经济运行双重因素下,实现去中心化的综合能源微电网分布式优化调度。基于MATLA仿真软件在IEEE-14节点系统中验证了算法的有效性;同时基于3台上位机和Lab VIEW-MATLAB联合仿真,实现了基于实时通信的3节点微电网系统经济性最优调度。

1 分布式综合能源微电网架构及建模

电网与通信网络的深度融合推动区域能源系统向大规模物理能源系统演化。微电网随之逐步向包括物理层(包含电力网络)、通信层(包含通信网络)以及控制层(运行分布式控制程序)的结构发展[7]。

微电网中太阳能、风能等可再生能源的接入比例逐步上升,降低了发电成本和环境污染。微电网的结构、发电装置以及储能装置都较为灵活,通过控制策略的合理配置,可以有效提高供用电效率,在满足供电质量的同时,还能够提高电网经济性指标。本文使用的多智能体一致性算法是在每个通信节点建立一个用于一致性优化的代理(Agent),各个代理之间通过通信网络进行实时通信,获取相邻节点的状态,如图1所示。每个代理基于相邻微源节点的信息与自身的状态,调节自身下属发电节点的出力,使下属节点和相邻节点的成本微增率趋于一致,进而实现分布式能量最优调度。

图1 综合能源微电网去中心化架构

多智能体系统通常是基于各个智能体之间的(通信)连接关系构建而成。通信网络的拓扑图通常使用G来表示,G=(V,E,A),其由n个节点的集合V、节点之间连接形成边的集合E以及节点之间的邻接矩阵A构成,其中,V={v1,v2,…,v i…,v n}、E⊆V×V。如果节点i与节点j之间存在双向信息交互,那么将形成边(v i,v j)和(v j,v i),并且(v i,v j)、(v j,v i)∈E。n个节点之间的连接关系将形成n×n的邻接矩阵A[8]。邻接矩阵A=(a ij)n×n可表示如下[9]

2 一致性算法和微源成本模型

2.1 一阶一致性方法

一致性算法是分布式多智能体系统中经典的控制方法,也可称为一致性协议[10]。其在较多领域中得到了广泛应用,如集群运动、同步现象以及有领导者和无领导者聚集问题等。该方法使用x i描述节点i的状态,那么各个节点最终的一致性目标是使各个节点的状态达到相同,即x1=x2=…=x n。为达到一致性目标,有多种控制方式,其中一阶离散一致性方法控制原理简单,且收敛速度较快,应用广泛。因此,本文采用一阶一致性算法进行一致性控制。在一阶一致性控制中,节点i的控制策略为

式中:k为离散时间步数;a ij为节点i和节点j的连接关系或连接强度;x j为x i的邻居结点;n为系统多智能体节点个数;N i为x i相邻节点的集合。

一阶一致性控制实质是一个简单PID控制中比例控制的应用,即采用自己与各个相邻节点间状态误差之和作为状态反馈量。调节的结果是:该节点的状态将向着相邻节点状态的加权平均值移动,这里连接关系a ij可以理解为权重。

2.2 综合能源微电网的综合成本模型及成本微增率

随着分布式能源渗透率的增加,综合能源微电网中电源也日趋多样化。为了提高能源的综合利用效率,通常还会对热能进行综合利用,基于微燃机的热电联产即为一个典型例子。分布式电源可分为可调度微源和不可调度微源。可调度微源有微燃机、燃料电池、含有储能单元的光伏发电装置以及储能装置;不可调度微源有风力发电以及不含储能的光伏发电装置。本文基于一致性的能量调度要求微源可调度,因此只针对可调度微源进行研究。通过调度可控微源,在满足系统能量供需平衡的前提下,达到经济性最优。对此,需要对可控微源进行发电供热成本建模,建模需要考虑微源的发电效率、供热成本、燃料成本以及维护和折旧等多种因素[11]。假设与其他微源相比,系统储能在某些条件下具有一定的经济性,如使用梯次利用的低成本储能,则为储能与其他微源之间的经济性能量调度提供了可能。通过热电联产,微燃机在发电的同时供应热能,可大幅提高整体的能源利用效率。最终系统有只发电的微燃机、热电联产微燃机、储能、带储能的太阳能光伏板和燃料电池,其综合发电成本可以统一简化为发电功率的二次函数模型[12-15],即:

式中:C i为发电与供热的总成本;P i、H i分别为单元的发电功率与供热功率;αi、βi、γi、θi、δi、φi为成本系数。当该模型表示只发电的微燃机时,有H i=θi=δi=φi=0。当表示为热电联产的微燃机成本时,P i、H i均大于0。当该模型表示储能成本函数时,有βi=γi=H i=θi=δi=φi=0,P i＞0表示储能放电,P i＜0表示储能充电[12]。系统经济性最优目标为

同时系统还需要满足电功率以及热功率供需平衡约束。为了简化模型,这里不考虑线损以及热量传输损耗,只须保证系统电功率和热功率的代数和分别为0即可

式中:PGi为节点i的发电功率;HGi为节点i的供热功率;PLi为节点i的负载功率;HLi为节点i的热负荷功率。

除了发电供需平衡的等式约束,还需要考虑各个微源发电以及供热容量上下限的不等式约束

在单因素试验的基础上，选取三个主要因子X1、X2、X3进行响应曲面试验设计，以叶黄素的提取量为响应值进行三因素三水平试验，运用Design Expert 10.0.7软件进行回归分析，确定稻谷中叶黄素的最佳提取方法。

发电成本C i对功率P i以及热功率H i分别进行求导,即可得到在功率P i、H i时,该节点的发电成本微增率为

从而可使用发电成本微增率d P,i d H,i以及成本函数参数αi、βi、φi、θi、δi表示电功率以及热功率。

发电功率的不等约束条件可变换为发电功率上下限以及一致性变量成本微增率d P,i、d H,i的函数

2.3 电力系统等微增率准则

在含不等式约束优化中,通常使用拉格朗日乘数法将不等式约束转换成等式约束。转换之后的系统优化目标将包含原始优化目标和不等式项。成本最优调度的目标函数转换成的拉格朗日方程为

优化目标是求得上述方程的最小值,这里即为系统的极小值,也是最小值。L对电功率P、热功率H求导,导数为0的点,即为系统的最优值。这里前提是系统的成本函数是凸函数,本文的成本函数为二次函数模型,且该二次函数系数均大于0,因此求得的极值点即为最小值点,系统总成本最小,有以下关系

在方程满足约束条件下,求得极值满足P i,min时,则方程成本微增率最优解为和。可得

由上述可知,在满足系统约束的条件下,仅当各个微源的发电微增率以及供热成本微增率分别趋于一致的时候,即趋于d*P和d*H的时候,系统才达到综合成本最小。当某个微源的发电供热功率达到其上下限,其功率将不再变化。其他的仍有剩余容量的微源将继续调节,直到这些微源的微增率趋于一致。此时系统将达到经济性最优[13]。

3 综合能源微电网一致性优化调度

具体的分布式一致性算法步骤如下。

(1)对初始电热成本微增率和初始电热功率进行初始化以及初始状态计算,即初始化系统的初始发电功率P i(0)和供热功率H i(0),同时计算出初始的发电及供热成本微增率d P,i(0)和d H,i(0),初始电和热功率不平衡y P(0)和y H(0)

(2)使用一阶一致性算法,对微增率d P,i、d H,i和功率P i、H i进行迭代,同时计算系统的电热功率不平衡y P和y H

式中:ρij为节点i、j之间的连接关系或者连接权重(下标P、H表示电功率和热功率);εi为功率不平衡的负反馈增益,该增益越大,系统功率平衡收敛速度越快,同时系统的稳定裕度也会减小。

通过不断迭代,微电网的电和热功率不平衡将趋近于0,同时各个可调节微源的发电和供热成本微增率也将分别趋于一致。当某一个节点的功率达到其功率上下限时,其功率将保持在上下限位置,并暂时等效为不可控微源,退出后续的调控,直到系统负载降低,其重新回到可调节区间。其余的有可调节容量的节点将继续进行一致性协调控制,直到剩余节点的成本微增率达到新的一致,同时系统达到功率平衡。根据文献[7]可以证明,系统最终收敛于最优发电供热成本微增率d*P和d*H,且电热功率均达到平衡。

4 算例与仿真结果分析

为验证本文算法在综合能源微电网中的有效性,本文首先在MATLAB中建立如图2所示IEEE-14节点综合能源微电网模型,其各节点的初始电功率、热功率以及成本函数系数如表1所示。然后在MATLAB中实现了基于微增率一致性的分布式发电功率最优分配。并且进一步在3台上位机电脑基于Lab VIE W-MATLAB联合仿真平台,实现了该算法在IEEE-3节点系统中基于实时通信的分布式最优调度实验。在14节点仿真中,节点7为储能节点(β7=0),节点2、3、6、10、12、14为热电联产节点以及热负荷。供电和供热的一致性迭代仿真结果分别如图3和图4所示。从图3(b)可看出,各个节点的发电成本的微增率最终均收敛到了5.19元/k Wh;图3(c)则显示,经过一致性迭代,功率缺额趋于0,最后达到供需平衡。在图4所示的一致性迭代过程中,包含热功率的节点2、3、6、10、12、14的热功率成本微增率达到一致性的同时,系统热功率也达到了供需平衡。此时电能和热能分配均达到各自最优,系统也达到全局经济性最优。

图2 IEEE-14节点综合能源微电网系统

表1 IEEE-14节点成本参数

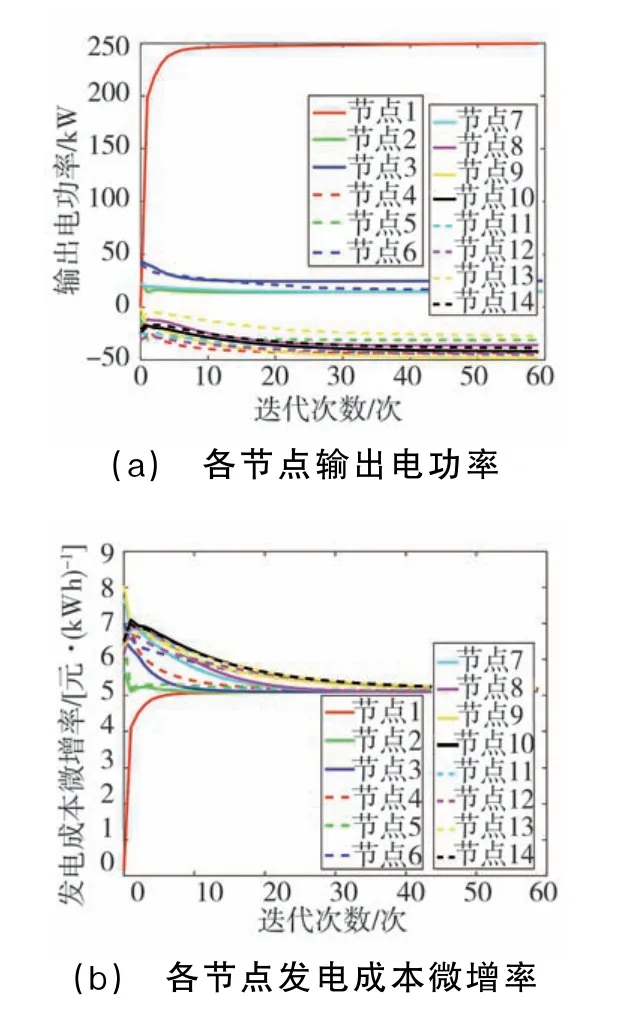
图3 IEEE-14节点系统一致性仿真供电结果

图4 IEEE-14节点系统一致性仿真热负荷结果

图5展示了包含3台上位机节点的分布式经济性调度仿真实验拓扑图。各个节点之间可以通过交换机和通信线路进行实时通信。在该分布式实验中,每台电脑通过MATLAB运行系统模型以及一致性算法。同时在该电脑中,利用Lab-VIEW良好的人机交互功能,实现对MATLAB中的算法节点的调用,并且完成该节点与其它节点之间的通信。

图5 实验平台整体示意

具体的实现步骤如下。

(1)在3台设备上建立系统模型以及实现各自的基于通信的分布式一致性算法。

(2)在3台设备上使用Lab VIEW平台创建VI,完成各个设备与交换机之间的IP地址与端口配置,建立用于各个节点之间通信的TCP连接。

(3)针对分布式设备设计分布式人机交互界面,对各个节点及其相邻节点状态进行实时监测。

(4)将分布式设备通过通信线连接至交换机,各个节点使用MATLAB程序接收相邻节点的状态信息,包括功率、成本微增率等信息,并调用该节点的分布式一致性算法,计算出该节点的功率分配。

(5)各个节点之间持续进行通信及一致性迭代,直到各个节点的成本微增率达到一致,且系统功率供需达到平衡。

人机交互界面显示最终的运行结果如图6,实验初始的与经过一致性算法迭代优化后的发电成本微增率及发电成本对比结果如表2-3所示。

图6 人机交互界面显示的发电成本微增率

表2 一致性算法迭代前后3台设备成本微增率的变化

由表2可知,1号、2号和3号机各不相同的成本微增率均收敛到了6.13元/k Wh,3个节点的总成本微增率降低了14.03%。实验结果表3则反映出,3台设备的发电成本从优化迭代前的162.85元/k Wh、194.4元/k Wh以及42.1元/k Wh分别变化到了100.98元/k Wh、65.29元/k Wh以及96元/k Wh,综合总发电成本从399.35元/k Wh下降到了262.27元/k Wh,下降了34.32%。

表3 一致性算法迭代前后3台设备发电成本的变化

该上位机实验说明了本文提出的分布式一致性功率分配算法显著降低了总的发电成本。通过优化前后3台设备的发电成本微增率和发电成本对比,可以看出成本微增率在一致性迭代过程中,微增率高的节点在降低微增率的同时,也在降低其发电功率和发电成本;而微增率低的节点在提高微增率的同时,也在提高其发电功率和发电成本。该过程实质是:通过微增率一致性来实现将系统负荷从发电成本高的节点转移到发电成本低的节点,从而实现整体发电成本的不断降低。在各个结点的发电成本微增率达成一致时,此时负荷的转移将不会带来系统整体发电成本的降低,此时系统功率优化达到局部最优,同时也是全局最优。

5 结论

本文针对综合能源微电网的功率调度问题,提出了基于多智能体一致性的分布式功率分配算法,通过实时调节各个微源的出力,使各个可控微源的发电与供热成本微增率分别达到一致,进而实现系统发电与供热功率的最优分配。在实验部分,首先使用MATLAB仿真平台,在IEEE-14节点的综合能源微电网系统中对综合能源微电网最优调度进行了算法的验证。并且在基于分布式实时通信的上位机上,基于MATLAB和Lab-VIEW软件平台的联合仿真,通过成本微增率的一致性迭代,实现了将系统功率从高成本微源向低成本微源的转移,进而实现了综合能源微电网的分布式能量最优调度算法。MATLAB仿真测试以及后续的基于分布式设备的实验均显示了本算法对于降低系统总体成本的有效性以及在现实中的可行性。后续研究将考虑线损和储能设备充放电切换的成本以及底层设备控制算法的影响。