Novel orbit-attitude combination mode for solar power satellites to reduce mass and fuel

Qingjun LI, Yi WEI, Zhigng WU, Jinping JIANG,*

a School of Aeronautics and Astronautics, Sun Yat-sen University, Shenzhen 518107, China

b School of Medical Information Engineering, Jining Medical University, Rizhao 276826, China

KEYWORDS Gravity gradient torque;Quasi-Sun-pointing attitude;Solar radiation pressure;Space solar power station;Sun-frozen orbit

Abstract Solar power satellite receives great attention because it can release the energy crisis and environmental problems in the future.However,the launch and maintenance costs are tremendous due to the large system mass and large fuel consumption to counteract space perturbations. To reduce mass and fuel, a novel quasi-Sun-pointing attitude in Sun-frozen orbit is proposed. The Sun-frozen orbit has a nonzero eccentricity vector that always points towards the Sun. The quasi-Sun-pointing attitude is a periodic solution of the Sun-pointing attitude angle. Although about 3%electricity must be given up because of the variation of Sun-pointing attitude angle,little control action is required to deal with the solar radiation pressure and gravity-gradient torque.The algorithm to obtain initial conditions is proposed. The influences of system parameters and structural flexibilities are studied. Simulation results reveal that the quasi-Sun-pointing attitude in Sunfrozen orbit dramatically reduce fuel consumption,the dry mass,and complexity of the control system. In addition, structural vibration is hardly induced by the gravity-gradient torque. Thus, the bending stiffness as well as the mass of the supporting structure can be reduced.

1. Introduction

Solar Power Satellite (SPS) will be a huge source of clean and renewable solar energy in the future.It generates severalgigawatt electricity in space using several-square-kilometer solar array and delivers it to the Earth through microwave or laser, which was firstly proposed by Glaser in 1968.The SPS is more advantageous than the solar plant on the Earth because of higher power density in space, longer exposure to the Sun, and immunity to the weather and atmosphere.It can not only alleviate the energy crisis and environmental problems,but also enhance economic, space, and national security.Thus, the technical feasibilities, social effects, and conceptual designs of SPS were widely studied by the U.S.,Japan, and China.

In the past 5 decades, many efforts were devoted to developing key technologies of the SPS and improving the economic feasibility for affordable electricity.However, the high cost is still a concern.The economic feasibility can be improved by the following 4 approaches. (A) Reducing the fuel consumption of the orbit and attitude controller can cut down the maintenance cost, including the cost of the fuel itself, the launch cost to Geostationary Earth Orbit (GEO), and the replenishment cost of the space robots.(B) The masses of most SPS concepts are larger than 1.0×10kg, which is a key factor to the high launch cost.Thus, reducing the mass of the SPS can reduce the cost directly. (C) The efficiencies of the solar radiation capturing, electricity generation, and power transmission should also be increased.(D) New technologies should be developed to reduce the manufacturing and launch cost.This paper focus on reducing the mass and fuel consumption of the SPS,based on the dynamic analyses and control studies of the orbit, attitude, and structure.

The Sun-Pointing(SP)attitude in GEO is the most popular combination for the SPSs. The SP attitude can maximize the solar radiation capturing efficiency of the solar array. However, the control of the SP attitude in GEO is not easy. On the one hand, the effects of the space perturbations on the orbit and attitude increase greatly as the size of SPS increases.For instance,the maximum value of the Gravity Gradient Torque (GGT) of the Abacus SPS is about 143000 N·m, which is 400000 times the control capacity of control moment gyro in International Space Station.Its orbital eccentricity also increases rapidly due to the Solar Radiation Pressure (SRP)and large area-to-mass ratio. Although some attitude-orbital coupled controllers were designed using ion thrusters,85000 kg fuel per year is required to maintain the SP attitude and GEO of the Abacus SPS. On the other hand, structural deformations and vibrations could be caused by space perturbations and orbit/attitude controllers.It was found that the gravity-gradient-induced structural deformation of an SP beam is proportional to the fifth-order of the length.The large-amplitude vibrations would further increase the attitude control errors and moments,and even cause structural instabilityor resonance.One solution might be increasing the structural stiffness of the supporting structure. However,increasing the stiffness often implies increasing the mass of the structure.

To avoid the above orbital and attitude control problems,some new orbits and attitude modes were proposed. McNally et al.studied the dynamic responses of an SPS locating in the geosynchronous Laplace plane, where the long-term effects of the Earth’s oblateness and the lunisolar gravity balance out each other. Compared to GEO, the geosynchronous Laplace plane saves large amounts of orbital control fuel and reduces the risk of space debris. Grafstudied the feasibility of nonzero eccentricity orbits to reduce the influences of SRP on the orbital eccentricity, based on the concept of Sun-Frozen Orbit (SFO).However, the literatureswere premised on the assumption of the SP attitude. It was found that the fuel consumption of SP attitude maintenance became dominating in geosynchronous Laplace plane.Therefore,attitude modes should also be studied to further reduce fuel consumption.

Apart from the SP attitude, the Gravity-Gradient-Stabilized (GGS) attitude is also adopted for some SPS concepts because of its simplicity and fuel saving, such as Sail Tower concept.Yet, the solar radiation capturing efficiency of the GGS attitude is only 31.9%of the SP attitude.Elrodinvestigated the Quasi-Inertial (QI) attitude of spacecraft to avoid the long-term influences of the GGT,so that the attitude control fuel can be reduced.Whereas,the variation of the Sun direction due to the Earth revolution was not considered. Sincarsin and Hughesproposed the concept of Quasi-Sun-Pointing(QSP)attitude to track the variation of the Sun direction based on the QI attitude. However, the literatureswere based on the assumption of GEO, thus lots of orbital control fuel was required.Apart from GEO,Li et al.studied the QSP attitude and QI attitude in Keplerian elliptic orbits.Whereas,the orbital perturbations were not considered.There is no research on saving both orbital and attitude control fuel of the SPS at the same time.

This paper proposes a more desirable orbit and attitude mode for SPSs, which is QSP attitude in SFO. There are two novelties of this new mode. Firstly, it can dramatically save the orbital and attitude control fuel because the long-term effects of the GGT and SRP are vanished. Moreover, the dry mass and technical requirements of actuators can be reduced significantly. Secondly, the vibrations induced by the gravity gradient could be decreased greatly.Thus,the bending stiffness as well as the mass of the supporting structure can be reduced. However, there are also some limitations of this paper.This paper focus on the conceptual validation,dynamic properties, and control of the QSP attitude in SFO, considering GGT and SRP. Other space perturbations are not involved.A simplified rigid-body model for the SPS is adopted to reduce simulation time.

The remainder of this paper is organized as follows. Section 2 establishes a simple orbit-attitude coupled model for the SPS. Section 3 briefly reviews the characteristics of the orbits and attitude modes for SPSs. The basic concept of QSP attitude in SFO and the method to obtain the initial conditions are studied in Section 4. The influences of system parameters on the QSP attitude in SFO are presented in Section 5. The attitude control and the effects of structural flexibility are investigated in Section 6. Finally, some conclusions are summarized in Section 7.

2. Orbit-attitude coupled model

To study the concept and characteristics of QSP attitude in SFO, a simplified orbit-attitude coupled model of the SPS is established in this section considering GGT and SRP.The following assumptions are made for simplicity:(A)the SPS is simplified as a rigid body; (B) out-of-plane motions, such as the variation of the orbital plane and the roll/yaw motion,are neglected; (C) the Earth-pointing attitude is not considered; and (D) the Sun rotates about the Earth in the orbital plane with a constant angular velocity ω. The parameters of Abacus SPSare adopted as an example.

The simplified model of the SPS is shown in Fig.1.The origin of the inertial coordinate system OXY is located at the center of the Earth.The Y axis points to the initial direction of the Sun. The SPS is simplified as a rigid body AB. Point C is the center of AB.The generalized coordinates of AB are the orbital radius r,the orbital angle θ,and the pitch attitude angle α.The angle between AB and the X axis is defined as γ=θ+α for convenience. The mass and the length of AB are denoted by m=2.5×10kg and l = 3200 m respectively. To describe the QSP in SFO, a new coordinate system OXY, the Earth-revolution angle β=ωt, and the SP angle φ=γ-β are introduced. The Yaxis always points to the Sun.

Fig. 1 Simplified dynamic model.

where w is the thickness of the solar array,as shown in Fig.2.The parameter κ = 1 is adopted unless stated, because w is very small compared to l.The terms -μmr/rand-3Jμκsin（2α ）/ 2r（ ） are respectively the gravitational force and the GGT. The dynamic equations can be rewritten using the generalized coordinates, which yields

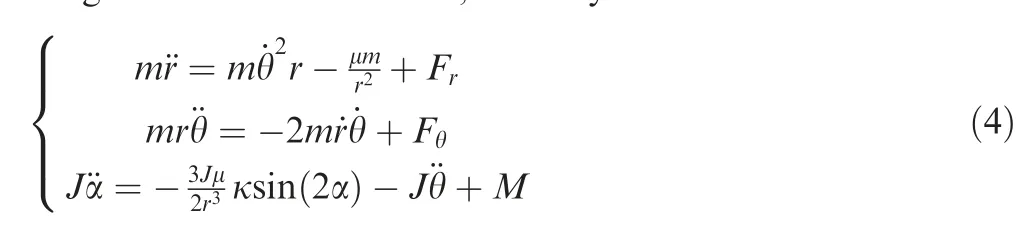
Fig.2 Three-dimensional schematic diagram(l,w,and h denote the length, thickness, and width of the solar array respectively).

It can be found from Eqs.(6)and(9)that the attitude of the SPS is a key factor to determine the SRP force.Besides,Eq.(4)indicates that the GGT is dependent on the orbital radius.Thus, the dynamic model is an orbit-attitude coupled model.

3. Preliminary concepts

Some preliminary concepts are briefly introduced in this section, including the SP attitude, QSP attitude, GGS attitude,GEO, and SFO.

3.1. Attitude motions in GEO

The most popular orbit in the previous studies of SPS is the GEO, because the simple ground track of GEO is advantageous to power transmission. Many attitude modes are investigated under the assumption of GEO.

The inertial attitude can be described by γ（t ）=0,as shown in Fig. 3. However, the variation of the Sun direction due to the Earth revolution is not considered. Based on the inertial attitude, the SP attitude tracks the variation of the Sun direction. The SP attitude can be described by φ（t ）=0 or n（t ） = u（ t ）. To study the effectiveness of the solar array to capture solar radiation,the capturing effectiveness is defined as η = n·u×100% = cosφ×100% （10）

The advantage of the SP attitude is that the capturing effectiveness is 100%.However,it can be seen from Eq.(4)that the control moment should counteract the GGT of the SPS.Because of large moment of inertia, 85000 kg fuel will be required every year for Abacus SPS, although high-specificimpulse ion thrusters are used.Thus, the fuel consumption in a 30-year lifetime will be 2550000 kg, more than 10 % of the total mass of Abacus SPS.Moreover,the structural deformations and vibrations due to the GGT increase rapidly as the size of the SPS increase.

Fig.3 Schematic of the GGS attitude,inertial attitude,and SP attitude(the rotation of Sun line is magnified by 10 times for clearness).

In order to avoid the large control moment and large structural deformations, many SPSs adopt the GGS attitude, such as Sail Tower and Tether SPS.The GGS attitude can be simply described by α（t ）=0,which is a stable equilibrium attitude of Eq.(4).Thus,the attitude control fuel due to GGT can be saved.Yet,the disadvantage of the GGS attitude is that the capturing effectiveness is only 63.7%if the solar panel is twoside, or 31.9 % if the solar panel is one-side.

The GGS attitude save attitude control fuel but has a low capturing effectiveness. In contrast, the SP attitude has a capturing effectiveness of 100%but consumes too much fuel.The QI attitude and the QSP attitude create an excellent balance between the capturing effectiveness and fuel consumption.Attitude control moment is not required for QI attitude and the QSP attitude.The QI attitude is a solution to Eq.(4)when M=0 such that the angle γ（t ）is periodic.The period of the QI attitude is one sidereal day.Based on the QI attitude,QSP attitude further considers the variation of the Sun direction, as illustrated in Fig. 4. The angle φ（t ） is periodic, and the period is one solar day. The advantages of the QSP attitude in GEO are that the capturing effectiveness is about 97.3 % and the control fuel to deal with the GGT can be reduced greatly.

3.2. Orbital motions with SP attitude

Although GEO is the most popular for SPS, it is influenced greatly by space perturbations. According to literature,the SRP-induced daily increase of the orbital eccentricity was about 1×10,and orbital control was required every 10 days.Because of the large area and large mass of the SPS, a great amount of fuel is needed to cancel the eccentricity growth due to SRP effects.

In order to reduce orbital control fuel, the secular SRP effects on the orbital motion should be avoided. The SRP effects were widely investigated,and the SFO was found to satisfy such requirement. The SFO was studied for the exploration of small asteroids and comets in the solar system.The mechanism of the SFO is briefly illustrated in Fig. 5.Under the assumption of this paper, if the initial eccentricity vector e is in Ydirection, ˙e will be in negative Xdirection.Then the eccentricity vector will rotate counter clockwise.The rotating rate of the eccentricity vector will be the same with ωif the magnitude of eis chosen aswhere a is the semi-major axis of the spacecraft,and gis the acceleration due to the SRP force that can be obtained from Eq.(6).Thus,the eccentricity vector will have a constant magnitude and points towards the Sun at all time.The eccentricity vector is look like frozen in OXY, as shown in Fig. 5.

4. QSP attitude in SFO

The basic concept of the proposed QSP attitude in SFO and the method to obtain initial conditions are presented in this section.

4.1. Basic concept

Prior to studying the dynamics and control, it is necessary to illustrate the basic concept of the QSP attitude in SFO, as shown in Fig.6.The eccentricity vector has a constant magnitude and points towards the Sun on average,which means that the perigee is at the positive Yaxis.There is no secular change of semi-major axis. And the spacecraft crosses the positive Xaxis once per solar day. In terms of attitude, the solution of φ is periodic. The period of φ is also a solar day.

At the initial moment,the Sun is at the positive Y axis,and OXYis coincident with OXY. The initial conditions of the QSP attitude in SFO are

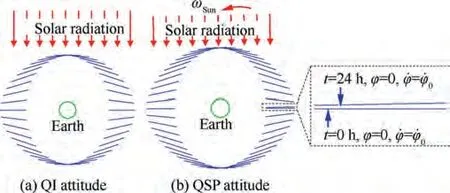
Fig. 4 Schematic of QI attitude and QSP attitude in GEO.

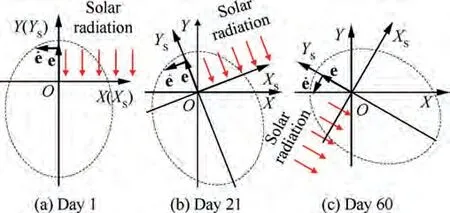
Fig. 5 Schematic of SFO.

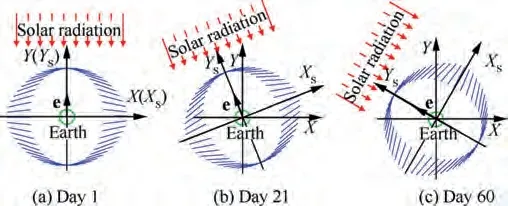
Fig. 6 QSP attitude in SFO.

In Eq.(16),ω is the argument of perigee measured from Xaxis, and ω=π/2. Thus, Δω denotes the angular error between the eccentricity vector and Yaxis.Although the orbital elements fluctuate with time, the variations become almost 0 at the end of a solar day.The eccentricity vector points to the Sun direction on average with a constant magnitude.

Fig. 8 gives the dynamic response of the SP angle φ. There are two maximal values in Fig. 8. The first one (0.421 rad) is larger than the second one (0.244 rad). Similarly, the second minimal value is smaller than the first one. The reason is that the first maximal point and the second minimal point are closed to the perigee, and consequently the GGT is larger.According to Eq. (10), the capturing effectiveness for the QSP attitude in SFO is shown in Fig.9,which can be obtained using one-side solar array.The lowest capturing effectiveness is 91.2 %, and the mean value is 97.1 %.

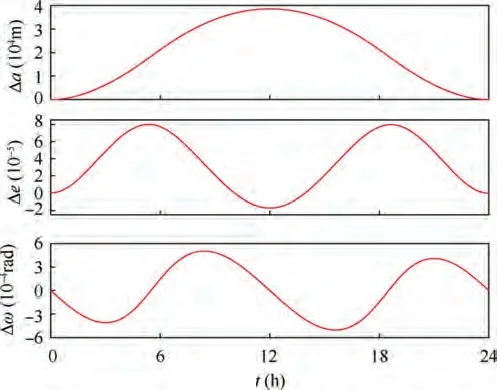
Fig. 7 Variation of orbital elements.

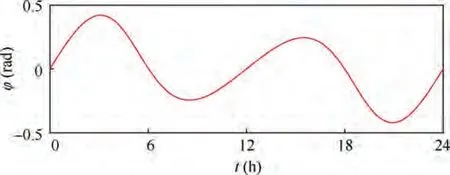
Fig. 8 Dynamic response of φ.

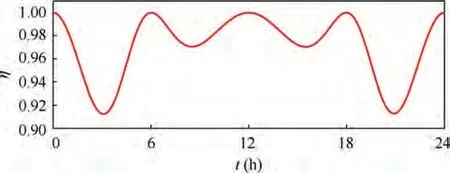
Fig. 9 Capturing effectiveness.

In summary,the SPS does not require any control action to obtain the proposed QSP attitude in SFO.It experiences small orbital variations and a 0.421-rad periodic attitude fluctuation.The novelty of the proposed QSP attitude in SFO is that the fuel consumption due to the GGT and SRP can be reduced dramatically, by giving up less than 3 % of electricity.

4.2. Initial conditions

The initial conditions of the QSP attitude in SFO is dependent on system parameters, such as area-to-mass ratio, reflection parameters, and parameter κ. The initial conditions of Eq.(15)can only be used for certain system parameters.It is essential to accurately calculate the initial conditions for different parameters, because the dynamic response is sensitive to the initial conditions.

Based on the above subsection, the initial condition problem can be transferred into an optimization problem: find e,a, and ˙α, then solve Eq. (4) to minimize the errors of final states in Eq. (13). However, this optimization problem is not based on the knowledge of SFO or QSP attitude. Moreover,it is not easy to solve this multi-variable multi-scale optimization problem very accurately. In this subsection, an iterative dichotomy algorithm is proposed to obtain the initial conditions accurately, based on the characteristics of SFO and QSP attitude.

Prior to presenting the iterative dichotomy algorithm, the influences of the initial conditions on the errors of the QSP attitude in SFO are studied.Numerical simulations are carried out for a time interval T using ain Eq. (15), different e, and different ˙α. The mass of the system is selected as m=2.5×10kg. The errors between the simulation results and the QSP attitude in SFO are defined as

The attitude and orbital errors in the simulations are depicted in Fig. 10 and Fig. 11 respectively. According to the numerical results, Δα（T ） increases monotonously with ˙α.But ehas little influence on Δα（T ）.Similarly,Δω（T ）decreases monotonously with e, but ˙αhas only small influence on Δω（T ）.The reason for the saltation in Fig.10 is that the initial attitude angle αis at an unstable equilibrium point and it rotates to different directions for different sign of ˙α. Fig. 10 and Fig. 11 imply that the coupling between the orbit and the attitude is not strong. Thus, the ˙αand ecan be roughly determined separately, and the coupling effects can be dealt with iteratively.

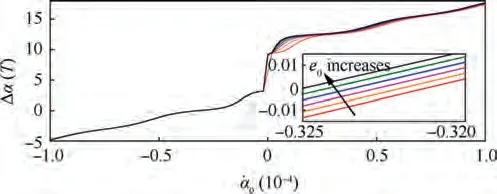
Fig. 10 Δα T（ ） for different initial values (e0 ∈[0，0.01]).

Fig.11 Δω（T ）for different initial values (˙α0 ∈[-5，-4]×10-4).

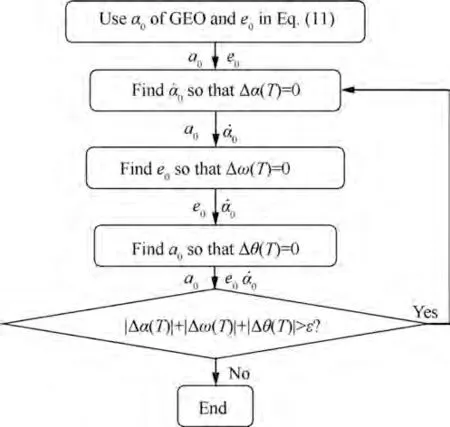
Fig.12 Algorithm to obtain initial conditions of QSP attitude in SFO.

In addition, the orbital period can be determined solely by the semi-major axis according to the knowledge of orbital mechanics. And the orbital period is reflected by the Δθ（T ）.Thus, the initial value of semi-major axis acan be obtained according to Δθ（T ）. Based on the above dynamic characteristics, the initial condition problem can be solved accurately by iteratively solving three single-variable equations. The proposed algorithm is shown in Fig. 12.

Step 1. Use aof GEO and ein Eq. (11).

Step 2.Use the initial conditions of aand e,solve Eq.(4),use the dichotomy to find the zero of the mapping from ˙αto Δα（T ）.

Step 3.Use the initial conditions of aand ˙α,solve Eq.(4),use the dichotomy to find the zero of the mapping from eto Δω（T ）.

Step 4.Use the initial conditions of eand ˙α,solve Eq.(4),use the dichotomy to find the zero of the mapping from ato Δθ（T ）.

Step 5.If ｜Δα（T ）｜+ ｜Δω（T ）｜+ ｜Δθ（T ）｜＞ε,go back to Step 2.Otherwise,the initial conditions of the QSP attitude in SFO are obtained.

In this algorithm,ε is the prescribed accuracy,which can be ε=10in simulations. By using this algorithm, the threevariable optimization problem is avoided.Each step is a problem of solving a single-variable mapping equation using dichotomy,which is easy and accurate.In practice,the dichotomy can also be replaced by other methods to improve the convergence speed.

5. Effects of system parameters

This section presents the effects of mass and geometric parameters of the system on the initial conditions and dynamic responses of the QSP attitude in SFO.

5.1. Orbital parameter

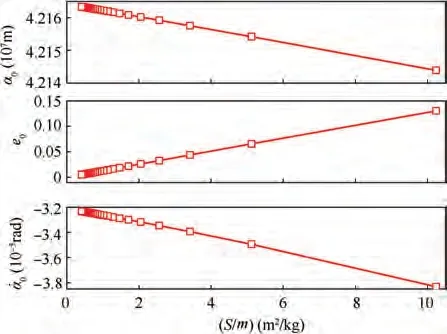
Fig. 13 Initial conditions for different area-to-mass ratio.

According to Eq. (6), the SRP acceleration is proportional to the area-to-mass ratio. Thus, this subsection studies the influences of area-to-mass ratio on the initial conditions using the iterative dichotomy algorithm proposed in the last section.To this end, the mass of the system varies from 1.0×10kg to 2.5×10kg. The numerical results are depicted in Fig. 13 and Fig. 14.

It can be seen from Fig. 13 that the area-to-mass ratio has great influence on the initial eccentricity. The initial eccentricity increases linearly with the area-to-mass ratio. This phenomenon agrees with the case of SP attitude in SFO, as shown in Eq. (11). When the area-to-mass ratio is 0.41(m=2.5×10kg), the initial eccentricity is about 0.005.When the area-to-mass ratio is 10.24 (m=1.0×10kg), the initial eccentricity becomes approximately 0.130. The initial semi-major axis and the initial attitude angular velocity are also influenced slightly.

The variation of the SP angle φ is related to the capturing effectiveness η through Eq. (10). The average and minimum η in the simulations for different m are depicted in Fig. 14. The average η remains almost unchanged when m increases, while the minimum value increases slightly. The average η reaches a maximum (97.3 %) when m=2.5×10kg.

From the above simulations, it can be found that the impact of m on the capturing effectiveness is small. But m has a great influence on the orbital eccentricity and initial attitude condition.

5.2. Attitude parameter

The parameter κ can influence the attitude motion of the spacecraft,and the orbital motion would be affected consequently. This subsection studies the effects of κ.

It can be seen from Eq. (4) that the parameter κ is a key parameter to the GGT.When κ=0,the GGT of the SPS vanishes.And κ is closed to 1 when w is much smaller than l.The initial conditions and the dynamic responses of the QSP attitude in SFO are studied when the parameter κ varies from 0.5 to 1 in this subsection. The mass of the SPS is selected as m=1.0×10kg to illustrate the attitude motion clearly.

The dynamic responses of φ for different κ are shown in Fig. 15. It can be found that the variation of the SP angle φ increases as the parameter κ increase.Fig.16 presents the average and minimum values capturing effectiveness. The minimum capturing effectiveness decreases with κ due to the increase of the variation of φ. The influence of κ on the average capturing effectiveness is mild.

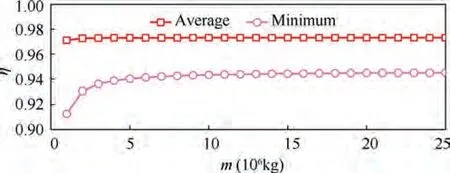
Fig. 14 Average and minimum capturing effectiveness for different m.

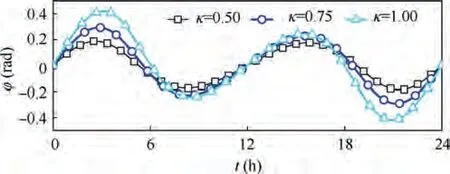
Fig. 15 Dynamic responses of φ for different κ.

Fig. 16 Average and minimum capturing effectiveness for different κ.

The influences of κ on the initial conditions are illustrated in Fig. 17. The initial attitude angular velocity ˙αincreases remarkably with κ. When κ increases, the fluctuation of φ becomes larger, which leads to the decrease of average SRP force. Thus the required initial orbital eccentricity eis also reduced according to Eq. (11).

In an extreme case of κ=0,the GGT of the SPS in Eq.(1)becomes 0.Then the SP angle φ can remains 0 without control moment,and the capturing effectiveness becomes 1.Some SPS concepts did use this parameter, such as the cylindrical SPS concept considered by NASA.However,the capturing effectiveness of cylindrical SPS is only 31.9 %, which implies the waste of solar array. Moreover, using small κ is unfavorable to reducing the structural mass of the solar array because it means large thickness. Therefore, large κ is suggested in the design of SPS to reduce structural mass if QSP attitude and SFO are adopted, because the influence of κ on the average capturing effectiveness of the solar array is less than 3 %.

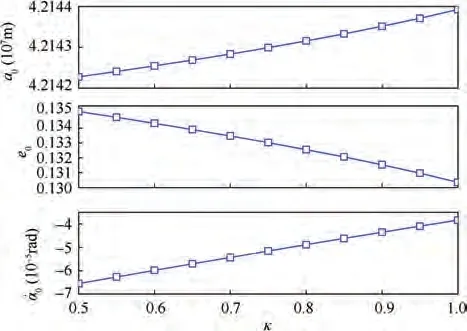
Fig. 17 Initial conditions for different κ.

6. Attitude control of flexible SPS

In the above sections,the rigid body model instead of a flexible model is used in order to reduce simulation time. This section further studies the effects of structural flexibility and attitude controller using an orbit-attitude-structure coupled model in literature.The rigid body AB in Fig. 1 becomes a flexible beam in this orbit-attitude-structure coupled model.The modelling method is a two-node Euler-Bernoulli beam element of absolute nodal coordinate formulation. The beam is dispersed into 10 elements with 4 coordinates in each node. Therefore,there are 44 degrees of freedom in total. The modeling procedure is not given for simplicity.

Before the simulations, it should be pointed out that the dynamic characteristics and the initial conditions of the QSP attitude in SFO are still reasonable for the flexible model in the case of small deformation. On the one hand, the attitude and orbit of the flexible model can be simplified to the rigid model. On the other hand, the influences of structural vibrations on GGT and SRP are negligible for small deformation cases.

Six cases are studied in numerical simulations.The Young’s modulus of the beam is 70 GPa, the density is 2700 kg/m,other parameters are shown in Table 1. Case 1 and Case 3 use a smaller mass and smaller bending stiffness to study the effects of structural flexibility.Case 5 and Case 6 are provided for comparison, which are SP attitude in SFO and QSP attitude in GEO.

The simple proportional-derivative control method is adopted to stabilize the QSP attitude in SFO, and the control moment is calculated by

Table 1 Six cases of the flexible beam control.

where ωis the control frequency, ζ = 1 is the damping ratio of the controller. It can be seen from Table 1 that the control of the SP attitude adopts a larger ω, which also means larger gains.The purpose is to reduce the control error of the SP attitude. The simulation results are shown in Fig. 18-Fig. 21.

It can be found from Fig. 18 that the variations of orbital eccentricities of Case 3, Case 4, and Case 6 increase linearly with time. The increasing rate of Case 3 is 5 times larger than Case 4,because the area-to-mass ratio of Case 3 is 5 times larger. The eccentricity of Case 6 is a little smaller than Case 3 because of the lower capturing effectiveness of the QSP attitude. In contrast, the variations of orbital eccentricity of Case 1 and Case 2 are less than 2×10,and the daily increases are even less than 10. This implies the structural flexibility has little influence on the SFO.

The maximum attitude errors of Case 3,Case 4,and Case 5 are 0.0234 rad, 0.0079 rad, and 0.0084 rad respectively, which are much larger than Case 1(0.0002 rad),Case 2(0.0004 rad),or Case 6 (0.00007 rad). The control error of Case 3 increases gradually with time,as shown in Fig.19.Generally,increasing the control frequency can reduce the control errors. However,although the control frequency of the SP attitude is larger,the control errors are larger than the QSP attitude due to the influence of GGT and structural flexibility. To conclude, the QSP attitude is not adversely influenced by the structural flexibility.

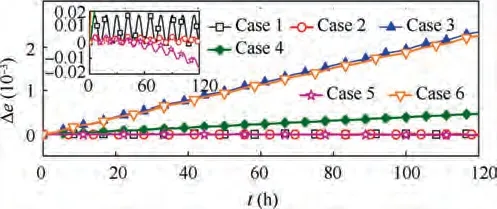
Fig. 18 Variations of orbital eccentricities.

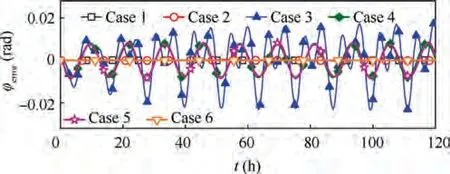
Fig. 19 Attitude control errors.

The maximum control moments of Case 3,Case 4,and Case 5 are 162396 N·m, 177835 N·m, and 187750 N·m respectively.Although the GGT of Case 3 is 5 times smaller than Case 4,the control moment of Case 3 is just a little smaller than Case 4.The reason is that the small bending stiffness of Case 3 causes large-amplitude structural vibrations,as shown in Fig.21.The large-amplitude vibrations increase not only the attitude error,but also the control moment of Case 3.Thus,the bending stiffness of the SP attitude is a key factor to reduce structural vibrations. The maximum control moments of Case 1, Case 2, and Case 6 are 12 N·m,68 N·m,and 21 N·m respectively.The control moment should be zero in the ideal case for the QSP attitude.Due to small amplitude structural vibrations,the attitude control moment becomes nonzero.

Fig.21 presents the vibrations of point A yin logarithmic scale.The vibrations are measured in the body coordinate system Cxyz. The vibration amplitude of Case 4 and Case 5 are about 11 m and 12 m,while Case 3 is about 550 m due to small bending stiffness.In contrast,the vibration amplitudes of Case 1, Case 2, and Case 6 are less than 0.13 m. Simulation results reveal another advantage of QSP attitude.Structural vibrations are hardly induced by GGT and attitude control moment for QSP attitude, while large-amplitude vibrations become a concern of large space structures for SP attitude.The reason for this phenomenon is that the distributed gravity-gradient force is counteracted by the concentrated control moment for SP attitude. The internal force of the structure is caused by the combined effects of the distributed forces and concentrated control moments. However, the distributed gravity-gradient force for the QSP attitude is counteracted by distributed inertial force due to attitude motion,which fortunately avoids the internal force as well as structural vibrations.Thus,the QSP attitude in SFO can avoid the problems of large vibrations,large attitude errors and moments,structural instability,and resonance in literatures. For SP attitude, vibration control of the SPS should be investigated seriously.

The simulation results indicate that the required control frequency, attitude errors, control moments, variation of orbital eccentricity, as well as the induced structural vibrations of the QSP attitude in SFO are 2 to 4 orders of magnitude lower than the SP attitude in GEO. Therefore, the second novelty is that the bending stiffness of the supporting structure can be reduced for QSP attitude in SFO, so that the mass of the supporting structure can be reduced greatly. The attitude maintenance of the Abacus SPS with SP attitude must be implemented by ion thrusters with high specific impulse, due to large control moment requirement shown in Fig. 20. However, control moment gyros are adequate to obtain attitude maintenance of the Abacus SPS with QSP attitude, which improve technical maturity.

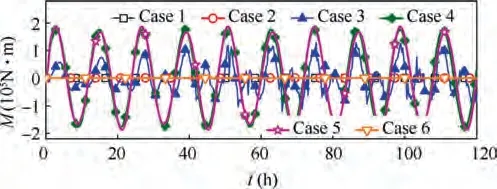
Fig. 20 Attitude control moments.

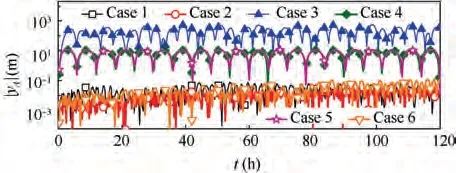
Fig. 21 Structural vibrations of point A.

In practice,the design of the orbit-attitude mode is coupled with other subsystems. While the QSP attitude in SFO contributes to saving fuel and reducing the structural vibrations,it also brings some adverse influences. For instance, the SFO increases the difficulties of microwave beam control,compared to GEO.However,we believe that reducing mass is a persistent goal of the SPS studies. The QSP attitude in SFO can be adopted when the microwave beam control technology is improved.

7. Conclusions

The QSP attitude in SFO is a periodic solution to the orbitattitude coupled dynamic equations in the presence of SRP and GGT.Control force or moment is not required in the ideal case.A method is proposed to obtain the initial conditions for different system parameters.It is an excellent selection for SPS to reduce mass and fuel greatly by giving up less than 3 % of electricity.

There are 4 advantages of QSP attitude in SFO compared to the SP attitude in GEO.(A)Little control action is required to counteract the GGT and SRP, so that a large amount of control fuel can be saved. (B) Since the control force and moment are much lower, the dry mass of the control system can be reduced significantly. (C)The complexity of the orbital and attitude control system can be reduced. For instance, ion thrusters can be replaced by control moment gyros for higher technical maturity.(D)The GGT-induced structural deformations and vibrations is diminished remarkably.Thus,the bending stiffness as well as the mass of the supporting structure can be decreased.

This paper focus on the conceptual validation of the QSP attitude in SFO, which provides new orbit-attitude combination mode for new SPS conceptual design.More accurate flexible multibody models of the SPS considering more space perturbations and more orbital and attitude control requirements could be considered in future works.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work is supported by the Guangdong Basic and Applied Basic Research Foundation (2019A1515110730).