Periodic event-triggered formation control for multi-UAV systems with collision avoidance

Tong WU, Jie WANG, Biling TIAN

a School of Artificial Intelligence, Hebei University of Technology, Tianjin 300130, China

b Institute of Artificial Intelligence, University of Science and Technology Beijing, Beijing 100083, China

c School of Electric and Information Engineering, Tianjin University, Tianjin 300072, China

KEYWORDS Collision avoidance;Distributed formation control;Event-triggered strategy;Leader-follower method;Multiple Unmanned Aerial Vehicles (UAVs)

Abstract In this paper, periodic event-triggered formation control problems with collision avoidance are studied for leader-follower multiple Unmanned Aerial Vehicles(UAVs).Firstly,based on the Artificial Potential Field (APF) method, a novel sliding manifold is proposed for controller design, which can solve the problem of collision avoidance. Then, the event-triggered strategy is applied to the distributed formation control of multi-UAV systems, where the evaluation of the event condition is continuous. In addition, the exclusion of Zeno behavior can be guaranteed by the inter-event time between two successive trigger events have a positive lower bound.Next,a periodic event-triggered mechanism is developed for formation control based on the continuous eventtriggered mechanism. The periodic trigger mechanism does not need additional hardware circuits and sophisticated sensors, which can reduce the control cost. The stability of the control system is proved by the Lyapunov function method. Finally, some numerical simulations are presented to illustrate the effectiveness of the proposed control protocol.

1. Introduction

The distributed formation control for multiple Unmanned Aerial Vehicles (UAVs) has attracted extensive attention in the past few decades.This is not only due to widespread applications of UAVs, such as wildfire monitoring,outdoor night showand target tracking,but also due to several advantages of multi-UAV systems compared with a single UAV,such as larger surveillance area, better operational capability and higher efficiency.One of the major topics to be investigated in formation control is the leading mode of multi-UAV systems, which can be divided into two categories, one is the leaderless formation controland the other is leader-follower formation control.Compared with leaderless formation control, the leader-follower formation control can track the leadership trajectory to keep desired formation pattern and accomplish a series of complex tasks.

In recent years, several significant results for formation tracking have been obtained. In Ref. 12, the distributed consensus theory is applied to formation controller design, while the robust performance of the formation tracking system is not mentioned. Then, the Sliding Mode Control (SMC) technique is applied to the distributed formation control, which can against external disturbances and improve the robust performance of the control system.In Ref.14,a robust adaptive controller is presented for the formation control system with model uncertainties.In addition,the method of combining virtual structure with output-feedback is adopted to achieve the asymptotic convergence of formation tracking error in Ref.15. To guarantee the safety of multi-UAV systems, collision avoidance should be considered in the design of the formation controller. At present, the methods of collision avoidance can be divided into optimization-based methodsand Artificial Potential Field (APF) methods.For optimization-based methods, the problem of formation collision avoidance can be solved by distributed model predictive controland linear programming.Nevertheless, the aforementioned optimization approaches meet difficulty in rapid implementation due to their high computational complexity. To avoid this problem, the APF approach is widely adopted because it has the advantages of small calculation and convenient implementation. In Ref. 18, a distributed formation control technique based on finite time theory is proposed, and the APF method is adopted to plan the collision avoidance path of each UAV.In Ref. 19 and Ref. 20, the improved repulsive potential function is combined with the distributed consensus method to achieve formation control. Considering the relative distance constraints of multiple agents on some special occasions, a novel distributed formation control scheme is presented,which combines the radial basis function Neural Network(NN)with the APF method.

In practice, continuous communication between agents may lead to large resource consumption and frequent updates of controllers, which is far from realistic. The event-triggered strategy becomes an effective way to solve these problems. In Ref. 22 and Ref. 23, a distributed event-driven cooperative control algorithm is proposed for first-order multi-agent systems to ensure state consensus. Then, the event-triggered consensus problem of second-order multi-agent systems is further investigated.To reduce the convergence time of distributed cooperative control, a finite-time event-triggered control protocol is proposed.Nevertheless, the system state needs to be continuously measured in most of the existing eventtriggered mechanisms,which requires additional hardware circuits and sophisticated sensors. To solve this problem, Anta and Tabuadaand Hu et al.investigate the self-triggered algorithm to avoid continuous monitoring of measurement errors, while the shortcoming of the self-triggered mechanism is too conservative to increase the inter event time. Recently,a novel periodic event-triggered mechanism (the event condition is evaluated periodically) is proposed, which overcomes the conservatism of the self-triggered mechanism and reduces the control cost.In addition,robustness is another important indicator to evaluate the performance of event-triggered control, and SMC based on the event-triggered mechanism can effectively guarantee the robust performance of the control system.Behera et al.and Wang et al.have further applied the SMC technique to the periodic event-triggered mechanism, which reduces the waste of resources compared with continuous event-triggered control. However, it is worth mentioning that there is still a lack of research on periodic event-triggered SMC for multi-UAV systems with collision avoidance, which motives this study.

In this paper, inspired by the event-triggered SMC methodand APF techniques,both formation tracking and collision avoidance problems for multi-UAV systems are studied. The main contributions of this paper are as follows:

Firstly, a novel sliding manifold is presented for formation controller design in leader-follower multi-UAV systems. This sliding manifold is designed based on the negative gradient of repulsive potential function and the formation tracking errors, which can solve the problem of formation tracking and collision avoidance simultaneously.

Secondly, the event-triggered strategy is applied to the formation control of multi-UAV systems,where the evaluation of the event condition is continuous.Moreover,the robust stability of the control system can be guaranteed by selecting an appropriate event condition, and the lower bound of the time interval ensures that Zeno behavior can be avoided.

Finally, a formation controller with the periodic eventtriggered mechanism is proposed for multi-UAV systems on the basis of the continuous event-triggered mechanism. In addition,the selection of sampling period and the upper bound of formation tracking errors are given to ensure the robust stability of the control system. The result shows that the periodic event-triggered formation SMC can be achieved for multi-UAV systems with collision avoidance.

The remainder of this paper is arranged as follows. In Section 2,the rigid UAV model is introduced and some definitions are given.On this basis,we also propose the control objectives of this paper.In Section 3,the APF method is introduced,the periodic event-triggered formation control protocol is presented, and the stability of the control system is analyzed.Then, the effectiveness of the proposed methods is verified by simulation experiments in Section 4. Finally, conclusions are shown in Section 5.

2. Preliminaries and problem formulation

In this section, some preliminaries and the analysis of rigid multi-UAV dynamics of this paper are formulated.

2.1. Notations

2.2. Graph theory

2.3. Problem formulation

The structure diagram of a quadrotor UAV is shown in Fig.1.Denote E=[E，E，E] as the inertial reference frame,B=[B，B，B] to be the body-fixed frame. Assume that the origin of the body-fixed frame is located at the mass center of a quadrotor UAV. p=[x，y，z]and Θ=[φ，θ，ψ]are represented as the positon and the attitude orientation of a quadrotor UAV in the inertial reference frame. φ∈R,θ∈R, ψ∈R are the roll angle, the pitch angle and the yaw angle respectively.

Suppose that the leader-follower multi-UAV systems with N+1 agents, which includes one leader indexed 0 and N followers indexed by 1 to N. In this paper, we focus on verifying the effectiveness of the collision avoidance algorithm based on the periodic event-triggered mechanism on the position loop of the multi-UAV system. According to the work in Ref. 37, the position dynamics of UAV i can be described as

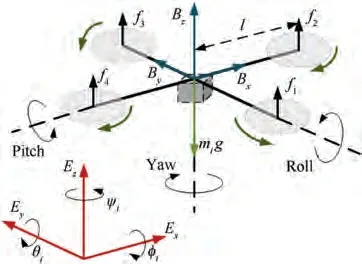
Fig. 1 The structure diagram of a quadrotor UAV.

where i=1，2，...，N, p（t）∈Rand v（t）∈Rare position and velocity of the i th UAV in the inertial reference frame. mis the total mass of the i th UAV, G=[0，0，mg]is the gravity factors,and g is the gravity acceleration.Here,assume that all the UAVs have fixed attitudes,and the influence of the attitude loop on the system can be seen as an equivalent control force.Then, the equivalent control force F（t） can be expressed as

Assumption 4. The measurement of local or relative position states is accurate, and there is no lag communication.

3. Primary results

3.1. Collision avoidance potential functions

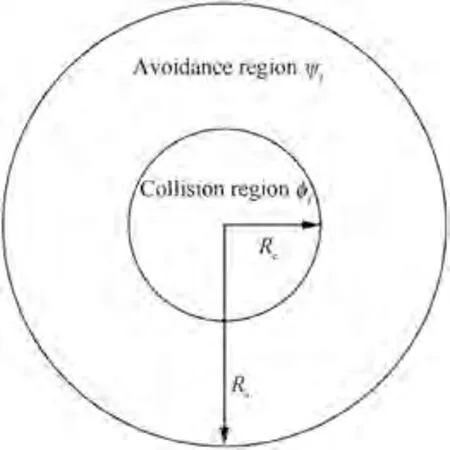
Fig. 2 Some defined regions for UAV i.

3.2. Continuous event-triggered formation control with collision avoidance

3.3. Periodic event-triggered formation control with collision avoidance

In a practical UAV system, most of the signal measurements or communications are carried out in discrete time, therefore,the continuous event-triggered mechanism is not applicable.In order to overcome this problem, the periodic event-triggered mechanism is introduced. The periodic event-triggered formation control only need to be evaluated periodically and it does not need additional hardware circuits and sophisticated sensors,which can reduce the control cost.In the following,based on the results in Section 3.2, the design of periodic eventtriggered mechanism is discussed.

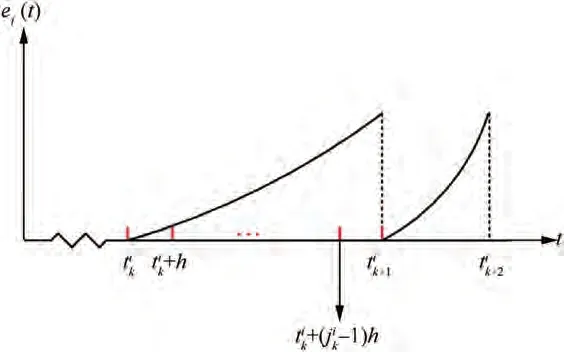
Fig. 3 Time evolution of ei（t） in periodic event-triggered mechanism.

Remark 5. In Section 3.2, because there may be a Zeno behavior in the continuous trigger mechanism, we discussed that the time interval Thas a lower bound to prove that there is no Zeno behavior. In Section 3.3, due to the sampling period h, the monitoring of events is discrete, and the time interval Tnaturally satisfies T＞h, so there is no Zeno behavior. Therefore, there is no need to discuss the lower bound of Tin the periodic eventtriggered mechanism.

4. Simulation results

The validity of the proposed theoretical results is verified by simulations. The undirected graph of multi-UAV system (4)-(5)is shown in Fig.4,which have one leader and three followers. The controller parameters are selected as c=0.5, k=5 and k=3.5, collision radius R=1.5 m, avoidance radius R=3 m, d（t）=[0.1 sin（t），0.1 sin（t），0.1 sin（t）]. The trigger parameters are selected as α=0.5, ε=3, τ=0.5, ε=0.7 and ε=0.5. The nonzero adjacency matrix coefficient a=1, the adjacency matrix A, the Laplace matrix L and the diagonal matrix B are given as

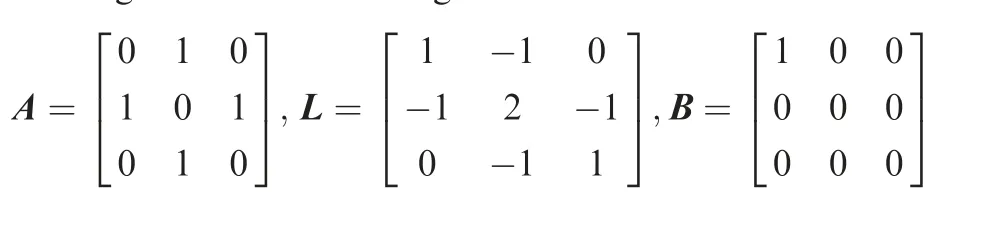
Fig. 4 Undirected communication topology.

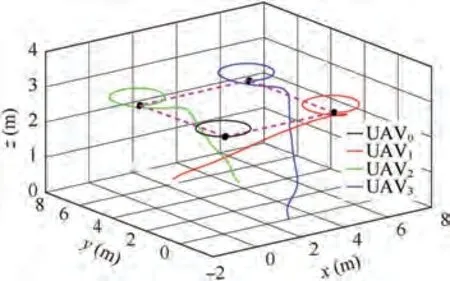
Fig. 5 Formation tracking trajectories of the UAVs.

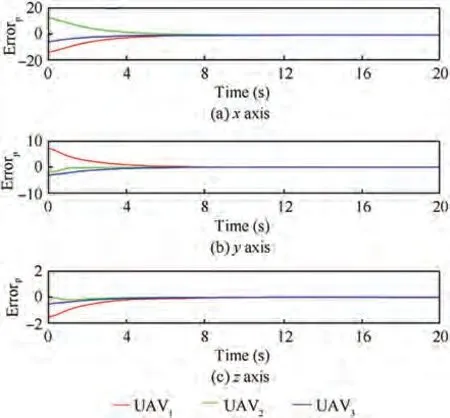
Fig. 6 Position tracking errors.

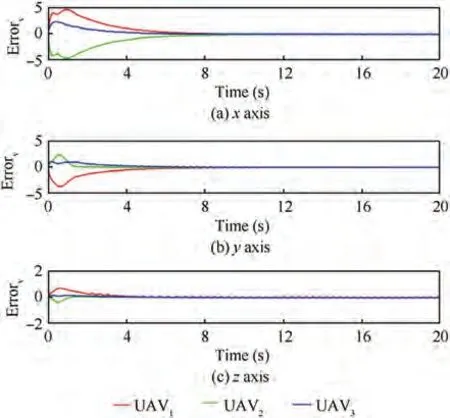
Fig. 7 Velocity tracking errors.

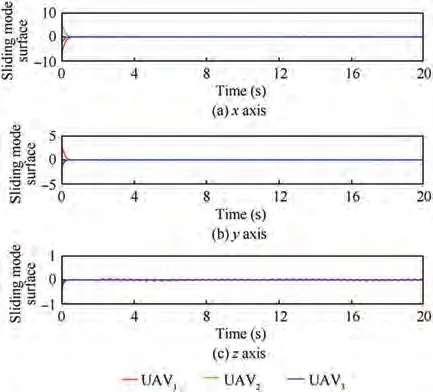
Fig. 8 Sliding mode surface.

Fig. 9 Relative distance between UAVs.

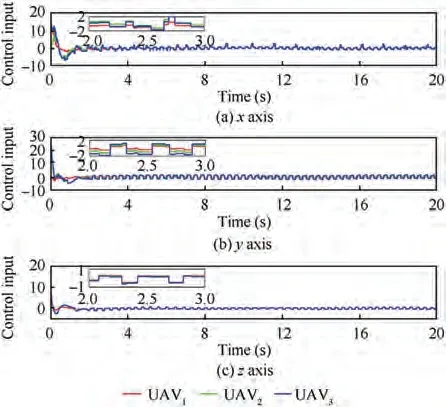
Fig. 10 Sliding mode controller with periodic event-triggered mechanism.

Fig. 11 Sampling interval generated by executing periodic event condition.

The initial states of three followers are selected as p（0）=[0， 3， 1], p（0）=[3， 3， 0.5], p（0）=[3， 0， 0],and the reference trajectory of the leader is set as p（t）=[sin（0.5t），cos（0.5t），3].

In this simulation, the leader-follower multi-UAV systems(4)-(5)under the sliding mode formation control protocol (17)with periodic event-triggered mechanism (39) is adopted. The sampling period is selected as h=0.005.

Fig.5 shows the formation trajectories of the UAVs,we can see that the three followers can track the leader and form desired formation. Figs. 6-7 present the position and velocity tracking errors between the UAVs. It can be obtained that the formation control and speed matching of multi-UAV system are achieved. The state trajectory of the sliding surface is shown in Fig.8,it can be inferred that the maximum boundary of the sliding surface is 0.074. Fig. 9 displays the relative distance between UAVs,which implies that the internal collisions among UAVs can be avoided.

The control inputs of the UAVs are depicted in Fig.10,and the control inputs is updated only when the event condition is violated.Fig.11 shows the triggering instants of the UAVs,in which the triggering times of three followers are 176, 126 and 136 respectively. Compared with continuous event-triggered formation control,the periodic event-triggered formation control does not need to continuously monitor the system state to evaluate event-triggered moment. That is to say, the periodic event-triggered formation control only need to be evaluated periodically and it does not need additional hardware circuits,which reduce the control cost.

5. Conclusions

In this paper, the leader-follower formation control problem of multi-UAV systems with collision avoidance is studied. A novel sliding manifold combined with collision avoidance repulsion field is proposed for event-triggered controller design, and the update of the controller is determined by the periodic event-triggered mechanism. The stability of the control system is proved by selecting an appropriate Lyapunov function, and Zeno behavior can be avoided because the inter-event time is lower bounded. Simulation results demonstrate the effectiveness of the proposed control scheme.Future work will further concentrate on event-triggered control of UAVs formation tracking with collision avoidance.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported in part by the Foundation (No.2019-JCJQ-ZD-049), the National Natural Science Foundation of China (Nos. 61703134, 62022060, 62073234,61773278). The China Postdoctoral Science Foundation (No.2019M650874). The Key R&D Program of Hebei Province(No. 20310802D), the Natural Science Foundation of Hebei Province (Nos. F2019202369, F2018202279, F2019202363).