An ECR-PCR rule for fusion of evidences defined on a non-exclusive framework of discernment

Xinyang DENG, Yebi CUI, Wen JIANG

School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS D number theory;Dempster-Shafer theory;Evidence combination;Non-exclusiveness;Proportional Conflict Redistribution rule;Information fusion

Abstract In the research of uncertain information processing, Dempster-Shafer Theory (DST)provides a framework for dealing with uncertain information,where evidence is defined on a Frame of Discernment (FOD) consisting of mutually exclusive elements. However, the requirement of exclusiveness on FOD sometimes is not satisfied,as shown in Dezert-Smarandache Theory(DSmT),a derivative of DST.In DSmT,the non-exclusiveness is expressed by propositions’intersection and the fusion of evidence is realized through a Proportional Conflict Redistribution (PCR) rule. In order to handle non-exclusive FODs, a new framework called D Number Theory (DNT) has been proposed recently, which quantifies the non-exclusive degree between propositions different from DSmT. In previous studies, an Exclusive Conflict Redistribution (ECR) rule has been designed in DNT to implement the fusion of evidence defined on a non-exclusive FOD, but there are some deficiencies in the ECR rule. In this paper, a new rule called ECR-PCR rule is proposed by combining the ECR and PCR rules to better implement the fusion of evidence defined on a nonexclusive FOD.Within the proposed rule,the definition of conflict utilizes the idea of ECR’s exclusive conflict,and the disposal of conflict is following the idea of PCR’s proportional redistribution.Properties of the ECR-PCR rule are presented.The effectiveness of the proposed new rule is verified through numerical examples and applications, in comparison with other fusion methods.

1. Introduction

Uncertain information processing is an important research direction in knowledge reasoning and artificial intelligence.Related theories for uncertain information processing include fuzzy set, rough set,and Z-number.Dempster-Shafer Theory(DST),also called evidence theory,provides an effective mathematical representation framework for uncertain information.Different from Bayesian theory, DST can directly express the uncertainty by using a set containing multiple elements, and thus it has advantages in expressing imprecision and unknowns.It has also been widely applied in many fields such as fault diagnosis,information fusion,decision making,classificationand general applications.

In DST,each piece of evidence is modeled as a Basic Probability Assignment(BPA)that is defined over a Frame of Discernment(FOD),and each element on the FOD is required to be mutually exclusive. However, the requirement of exclusiveness on FOD sometimes cannot be satisfied, as shown in Dezert-Smarandache Theory (DSmT).Three models called free DSm model,hybrid DSm model and Shafer’s model are proposed in DSmT in view of the relationship between elements among the FOD,as shown in Fig.1.In addition,a Proportional Conflict Redistribution (PCR) ruleis proposed to combine evidence by redistributing the conflict generated during the combination process in proportion,which is different from the global normalized allocation to conflict in the Dempster’s rule of DST. As a representative theory for processing information on a non-exclusive FOD, DSmT has attracted a lot of attention.However, in the three basic models of DSmT, they only define a completely exclusive or non-exclusive relationship between elements among the FOD but do not quantify the degrees of non-exclusiveness between elements.

Recently, a new theory called D Number Theory(DNT)provides an alternative processing framework for the evidence defined on a non-exclusive FOD by quantifying the non-exclusive degree between propositions in FOD,which has been used in many fields.In DNT, a model called D numberis used to express the evidence defined on a non-exclusive FOD. An Exclusive Conflict Redistribution (ECR) ruleproposed in this theory is provided to deal with the problem of evidence fusion when there is non-exclusiveness between elements on the FOD. In the ECR rule, the conflict between D numbers to be fused is handled by global normalization, which is the same as Dempster’s fusion rule. However, the results produced by using that normalization are sometimes counter-intuitive, which will be shown later in this paper.

Therefore,a novel fusion rule called ECR-PCR rule,a combination of the Exclusive Conflict Redistribution (ECR) and Proportional Conflict Redistribution (PCR) rules is proposed in this paper to improve the above-mentioned problems.Based on the DNT framework,the ECR-PCR rule fuses the evidence defined on a non-exclusive FOD by combining the idea of redistributing conflict proportionally of PCR rule in DSmT and the characteristic of quantifying non-exclusive degrees in ECR rule under DNT. Compared with the original ECR and PCR rules, the proposed ECR-PCR rule overcomes their shortcomings and is able to be applied in more real-world scenarios.First,different from the models given in the DSmT that only define 100%exclusivity or non-exclusivity,the ECR-PCR rule allows one to deal with various non-exclusive degrees between propositions in FOD during the fusion process. Second, the ECR-PCR rule can achieve more reasonable results when fusing highly conflicting or completely conflicting evidence, whereas the ECR rule is invalid in dealing with such problems. To verify the effectiveness of our proposed rule,comparison and discussion of the fusion results obtained using the proposed rule and other rules are illustrated in detail through numerical and application examples.

The remainder of this paper is organized as follows. Section 2 gives a brief introduction about DST, DSmT and DNT.In Section 3,the weaknesses of PCR rule and ECR rule are analyzed and the ECR-PCR fusion rule is proposed. Section 4 gives numerical examples to briefly illustrate the effectiveness of the proposed method. An application about forest fire detection is used to verify the rationality of the newly proposed method in Section 5.Finally,Section 6 concludes the paper.

2. Preliminaries

Some basic concepts and definitions about DST, DSmT and DNT are briefly introduced in this section.

2.1. Dempster-Shafer theory

DST has been widely used in various fields.In this subsection, some basic definitions of DSTare given.

Definition 3. For a BPA,its associated belief measure Beland plausibility measure Plare defined as

Fig. 1 Venn diagrams of three models in DSmT.

2.2. Dezert-Smarandache theory

A few concepts of DSmTare given as follows.Definition 6. Given a FOD Θ, select the corresponding model from the following three models.

(1) Free DSm model. There are no constraints on the elements of the FOD, written as M（Θ ）.

(2) Hybrid DSm model.The elements on the FOD involve both continuous concepts and exclusive assumptions,which are defined as M （Θ ）.

(3) Shafer’s model. All elements on the FOD are mutually exclusive, denoted as M（Θ ）.

DSmT offers PCR rule to implement the fusion of evidences.In this paper, the PCR rule mentioned below all refers to PCR6 (version 6) rule.

Definition 7. Assuming that mand mare two BPAs defined on a FOD Θ,the PCR formula for the fusion of mand mis

2.3. D number theory

As an extension of the classical theory of belief functions,DNTalleviates some limitations of DST, which has been applied in many fields. Most applications of DNT are based on its non-exclusiveness among elements of FOD. For example, in order to evaluate the quality of green suppliers in a fuzzy environment, DNT is used to model the nonexclusiveness between fuzzy numbers.For a risk of preventive maintenance planning, D numbers are utilized to express non-exclusive linguistic grades to develop a risk-based multicriterion decision-making approach.Some basic concepts on DNT are briefly introduced below.

Assume that we only know the non-exclusive degree between elements in FOD, and then the non-exclusive degree between propositions can be calculated as

3. Proposed method

3.1. Examples and analysis of PCR and ECR rules

In this subsection, some examples are given to show the deficiencies of PCR and ECR rules on the fusion of evidences defined on a non-exclusive FOD.

First, numerical examples mentioned in Ref. [62] are used to illustrate the results obtained by the PCR rule.

According to the above combination results, we find that the PCR rule has the following characteristics:

(1) The belief of each proportion in the combination result is calculated through a pattern similar to the conjunctive rule, and the conflict between two BPAs is proportionally redistributed to the non-empty propositions involved in the conflict. From a logical point of view, the pattern of redistributing conflict in the PCR rule is reasonable. It not only retains the data characteristics in the original information during the fusion process, but also avoids the invalid transfer of conflict.

Table 1 Combination results for hybrid DSm model in Example 1.

From the fusion result, we find that the belief of each proposition in the fusion result varies with the change of nonexclusive degrees u（A，B），u（A，C） and u（B，C）. In a special situation that u（A，B）=u（A，C）=u（B，C）=0, the ECR rule degenerates to the Dempster’s rule.The result obtained at that time becomes m（C ）=1, which is counter-intuitive.

The above example shows that the ECR rule may produce unreasonable result when dealing with highly conflicting evidences. A more extreme example is given below.

3.2. Proposed ECR-PCR rule

In this subsection,a novel fusion rule called ECR-PCR rule for the combination of evidences on a non-exclusive FOD is proposed. The ECR-PCR rule synthesizes the ideas of PCR rule and ECR rule, moreover, it overcomes the shortcomings in the two rules respectively.

Definition 13. Let D，Drepresent two D numbers defined on a non-exclusive FOD Θ,and the proposed ECR-PCR rule for the combination of Dand Dis defined by Eq. (22), where A，B，C ∈2, and u（B，C） and u（A，B） represent the nonexclusive degree between propositions B and C，A and B,respectively.

Fig. 2 shows how the fusion result changes with u（A，B）. It can be seen that the curves of D（A ）and D（B ） are overlapping and decrease with the rise of u（A，B）, which is opposite to the trend of D（{A，B}）.At the two endpoints,the results are quite different. When u（A，B）=0, it corresponds to the Shafer’s model in DSmT or classical DST framework, and the result is D（A ）=0.5，D（B ）=0.5, which is the same as the result of applying PCR rule. When u（A，B） takes the value 1, the combination result of using the ECR-PCR rule is D（{A，B}）=1,which is actually the same as the result generated by the DP rule. Thus the ECR-PCR rule obtains reasonable results and is effective in this example.

From the above examples, we have the following observations about the ECR-PCR rule:

(1) Compared with the PCR rule, the ECR-PCR rule

Fig. 2 Combination result generated by ECR-PCR rule in Example 5.

involves quantified non-exclusive degrees when there is partial exclusivity between elements on the FOD, which is not considered in the free DSm model, hybrid DSm model and Shafer’s model under the DSmT framework.

(2) Compared with the ECR rule, the ECR-PCR rule has improved the way of handling conflict.The same point with the ECR rule is that the quantity of Kis regarded as the conflict. However, different from the global redistribution of conflict,the ECR-PCR redistributes conflict proportionally by referencing the idea of PCR rule.

In addition, it can be easily found that the proposed ECRPCR rule satisfies the following properties:

4. Numerical examples

In this section, some numerical examples are used to illustrate the effectiveness of the ECR-PCR rule proposed in this paper.

Table 2 Intersection table to show the intermediate calculation process of ECR-PCR rule in Example 6.

Now,we can compare the results obtained by the proposed ECR-PCR rule with results obtained by other methods,including ECR, PCR and DP rules. Table 3 gives the combination results generated by different rules. Besides, for the sake of decision, the plausibility measure of each element in the combination results are also calculated, as shown in Table 4. In addition,Fig.3 shows the comparison between the plausibility of θand θfrom the combination results of the ECR-PCR and ECR rules.

(A) Comparison with DP rule.To start with,the combination result obtained by using the DP rule is the same as that obtained by using the ECR-PCR rule when u=1, which can be derived from Table 3. However, the DP rule is not able to reflect the impact of non-exclusiveness on the combination result, since it does not consider the non-exclusive degrees that may exist between elements on the FOD, so it is not applicable for the fusion of evidences on a nonexclusive FOD.

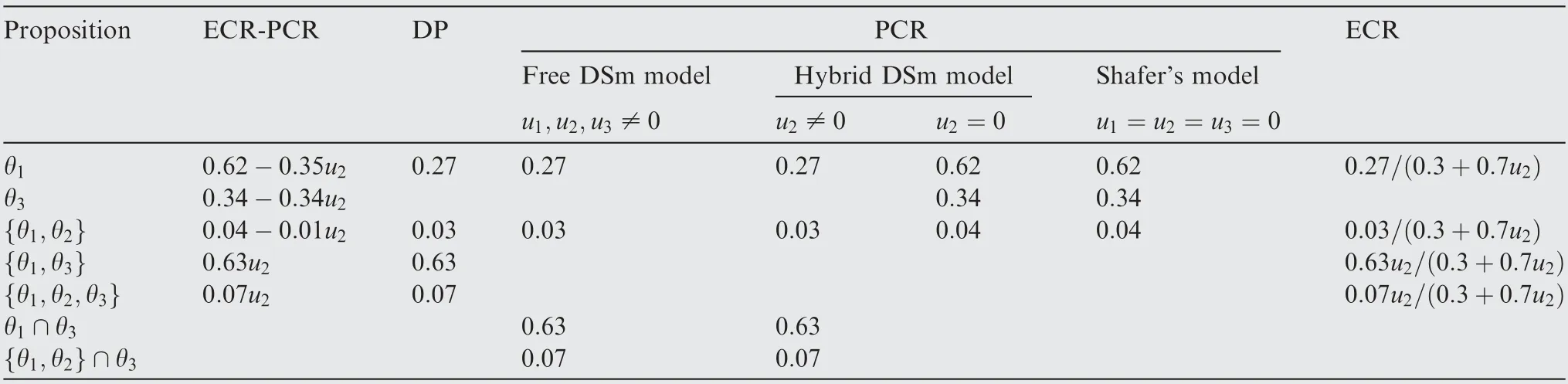
Table 3 Combination results of Example 6 using ECR-PCR, DP, PCR and ECR rules.

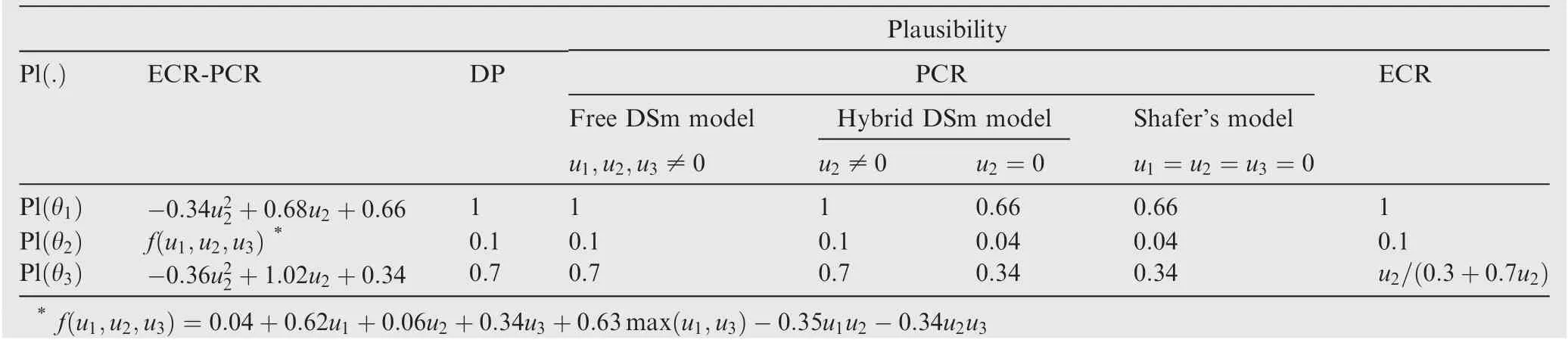
Table 4 Plausibility of each element in the combination results of Example 6.

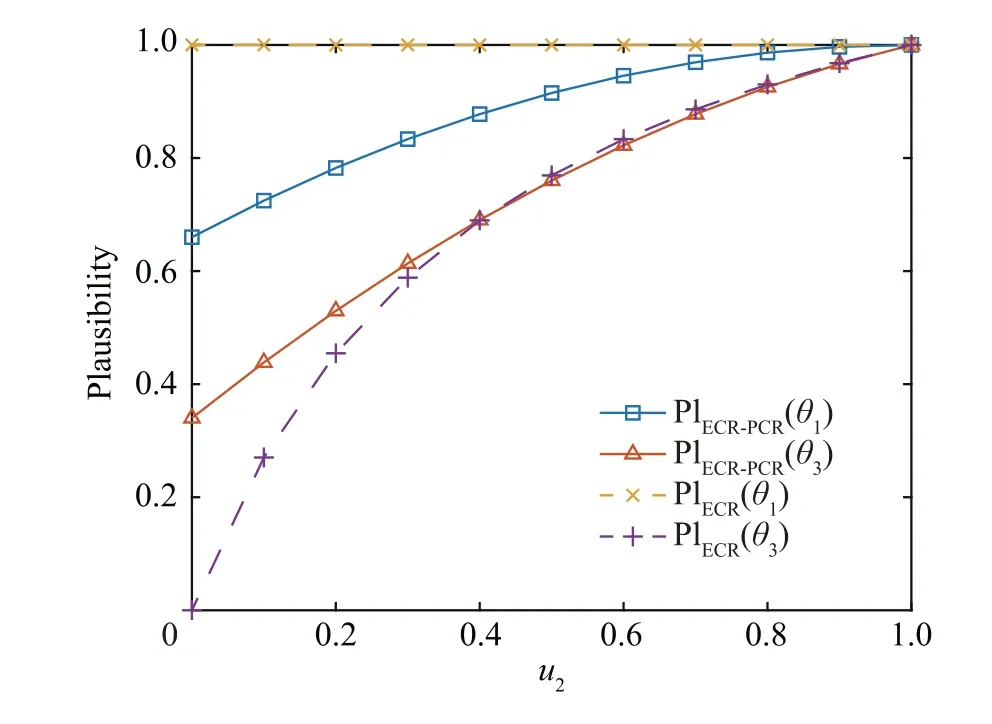
Fig. 3 Plausibility measure of θ1 and θ3 using ECR-PCR and ECR rules.

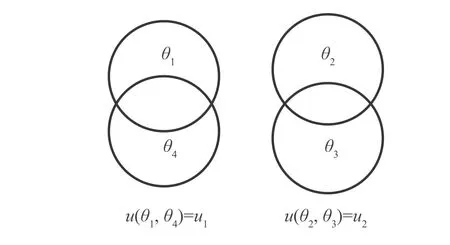
Fig.4 Schematic representation of non-exclusive degree between elements in FOD Θ.

(1)Evidence combination by using the proposed ECR-PCR rule

In terms of the proposed ECR-PCR rule, the following combination result is obtained. The intersection table exhibiting the intermediate calculation process of the ECR-PCR rule is shown in Table 5.

(2) Results comparison of different combination methods

In order to facilitate the comparison between the ECRPCR rule proposed in this paper and other rules such as ECR, PCR and DP rules, the combination results obtained by different rules are given in Table 6,and associated plausibility measures of elements in the combination results are shown in Table 7.

(A) Comparison with DP rule.From Table 6 and Table 7,the result of ECR-PCR rule varies with the change of uand u,showing a reasonable trend of change.By contrast,the result obtained by the DP rule keeps unchangeable in spite of the values of uand u, thus the influence of nonexclusiveness in FOD is not reflected in the DP rule.

(B) Comparison with PCR rule. As for the PCR rule,according to the different values of uand u, the obtained results correspond to different models under the DSmT framework.The PCR rule is only applicable to a few typical values of uand u,but does not display a process with the change of non-exclusive degrees.

(C) Comparison with ECR rule. Based on the ECR rule,the obtained result changes continuously with the change of uand u, which is more reasonable than the DP and PCR rules. But in the case of u=u=0, the ECR rule is inapplicable.

Furthermore, the relationship of plausibility measures between different pairs of elements obtained by using ECRPCR, PCR and ECR rules is given in Table 8.

From this table, it is found that compared with the ECR and PCR rules, the ranking of plausibility measures obtained by the ECR-PCR rule is changing under different conditions regarding the values of uand u. For example, whenu=u, the PCR rule obtains the ranking Pl（θ）=Pl（θ）＞Pl（θ）=Pl （θ）, while it is Pl（θ）=Pl（θ）=Pl（θ）=Pl（ θ）by the ECR rule under the same condition. By contrast, the ranking obtained by the ECR-PCR rule is Pl（θ）=Pl（θ）＞Pl（θ）=Pl （θ） for u=u= 1 and Pl（θ）=Pl（θ）=Pl（θ）=Pl （θ） for u=u≠1, which is more reasonable since the ECR-PCR rule has further distinguished the condition u=u.

Table 5 Intersection table to show the intermediate calculation process of ECR-PCR rule in Example 7.

5. Application

In this section,forest fire detection from Ref. [64] is employed to further illustrate the application of the proposed ECR-PCR rule.

In Ref.[64],forest fires are divided into three types,including Fire(F),Intermediate Fire(IF)and No Fire(NF).The fire detection is carried out in two cases in terms of whether link failure occurs or not. In each case, there are three classifiers

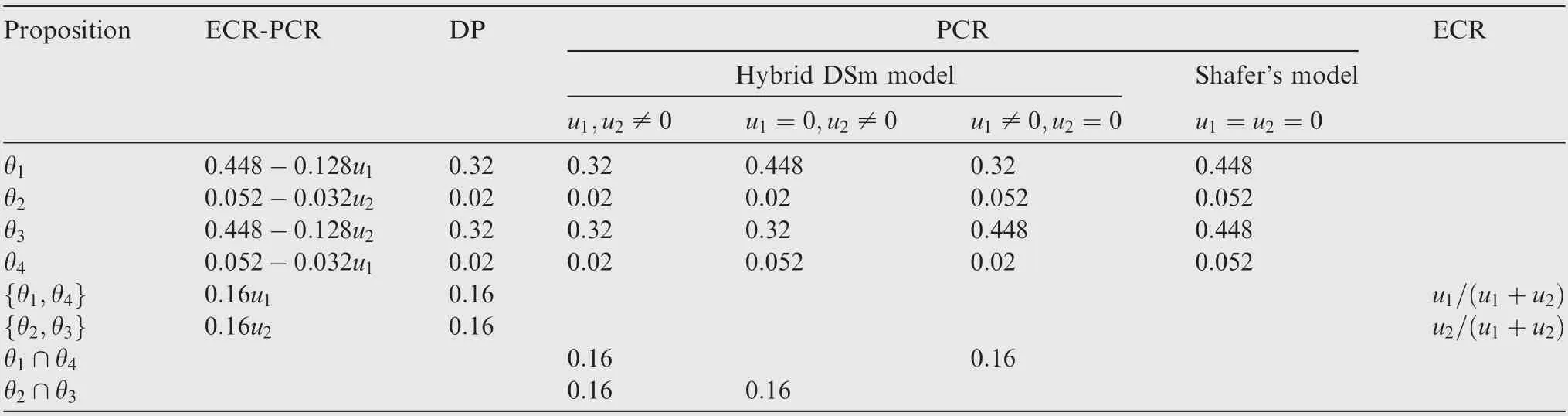
Table 6 Combination results of Example 7 using ECR-PCR, DP, PCR and ECR rules.

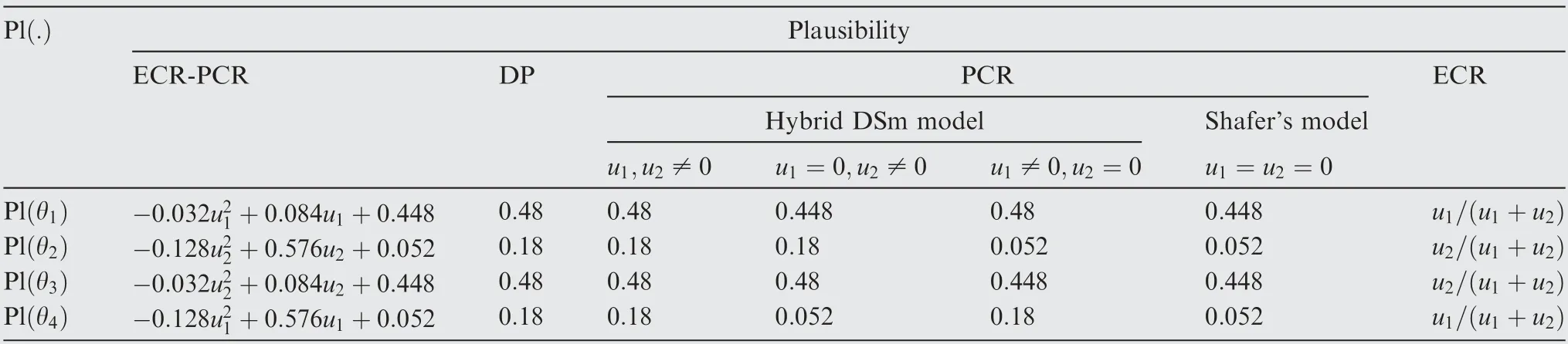
Table 7 Plausibility of each element in the combination results of Example 7.

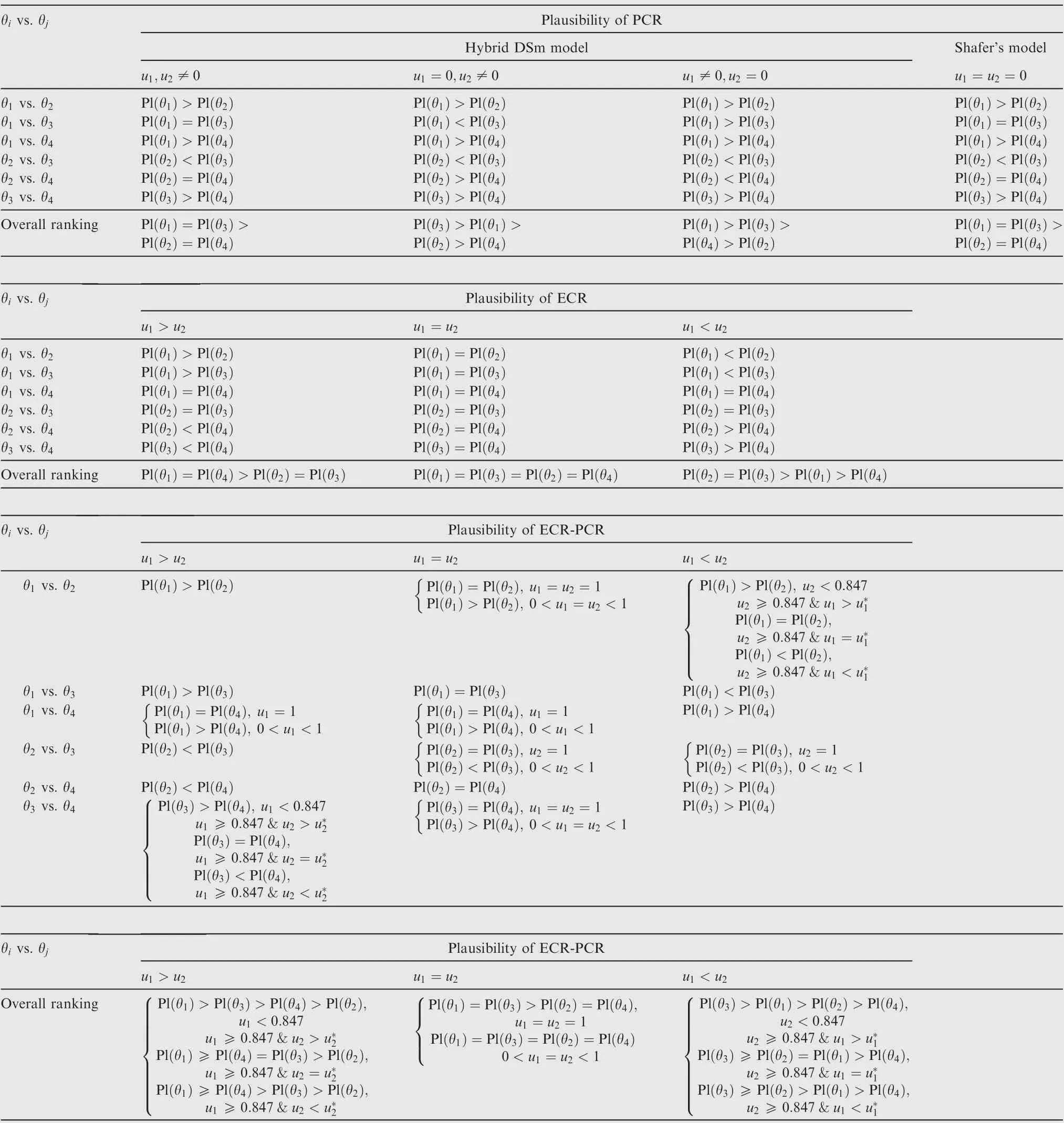
Table 8 Relationship of plausibility measures between different pairs of elements.

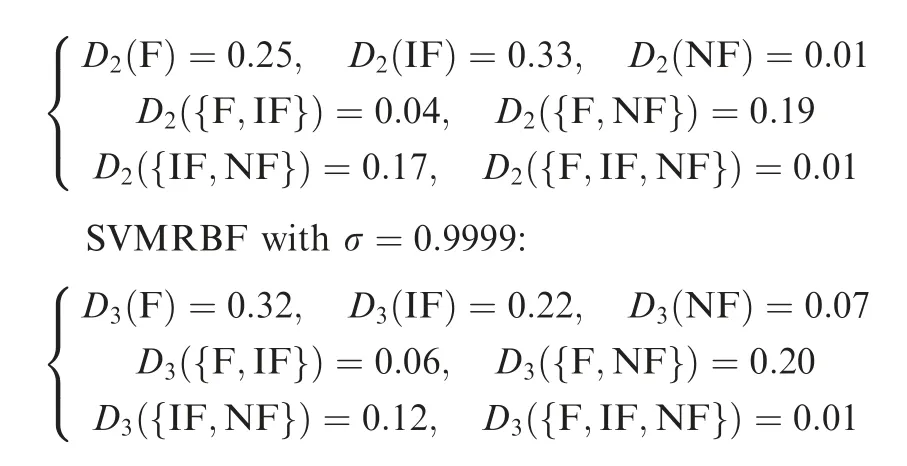
In this application, since there are three pieces of evidence to be combined, the proposed ECR-PCR can only combineevidence one by one, and it does not satisfy the associativity,therefore a scheme of Weighted Average Combination(WAC) is utilized to implement the combination of multiple pieces of evidence, as same as that shown in Ref. [47].

Table 9 Combination results using ECR, PCR and ECR-PCR rules in Case 1.

We assume there are n D numbers to be combined.At first,these D numbers are averaged with equal weights to derive an averaging evidence ¯D

The combination results in terms of different combination rules are shown in Table 9, which gives the beliefs of propositions I,IF,NF and CNS.It can be seen from Table 9 that the beliefs of CNS calculated by the ECR-PCR and ECR rules under corresponding conditions are all smaller than the results obtained by the PCR rule, while the beliefs of singletons are opposite in which singleton F has a relatively higher belief in the results of ECR-PCR and ECR rules than the PCR rule.Therefore, ECR and ECR-PCR rules provide more effective results for the fire estimation decision-making than PCR rule.

Besides, under the DSmT framework, only Shafer’s and hybrid DSm models are available in this application, which correspond to the cases of u=0 and u=1, respectively. For this reason, the PCR rule only obtains discrete results at these two points. By contrast, the ECR and ECR-PCR rules can provide a series of results with the change of u, as shown in Fig. 5.

From Fig. 5, in the results of both ECR-PCR and ECR rules,the beliefs of singletons decrease with the rise of u,while D（CNS）increases in the process.For any value of u,the ranking of singletons is always D （F ）＞D（IF ）＞D（NF ）,which indicates that the obtained result is robust.Therefore,in this case,F (Fire) is the most probable fire estimation.

Secondly, let us consider the case with link failure.

Case 2 With link failure

In this case,the estimations obtained by three classifiers are as follows.

SVM:

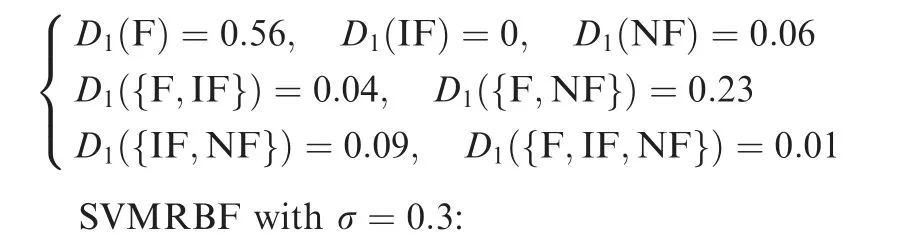
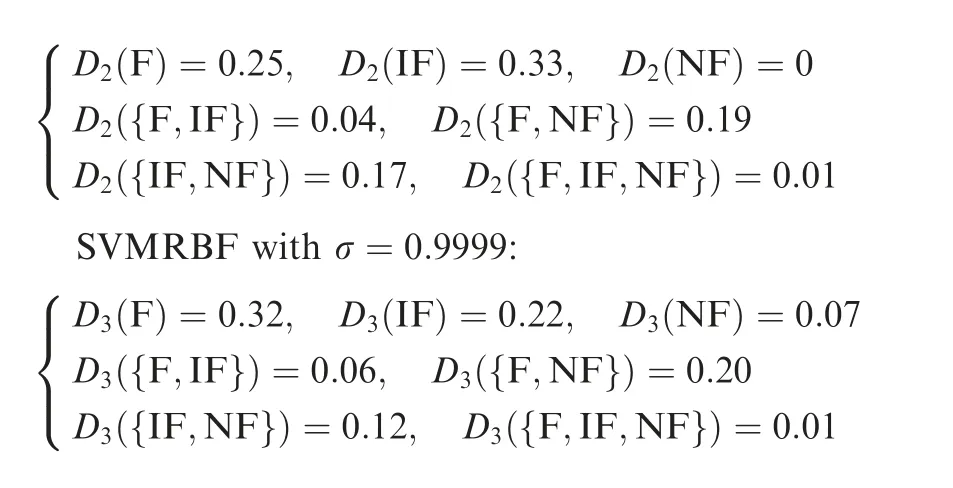
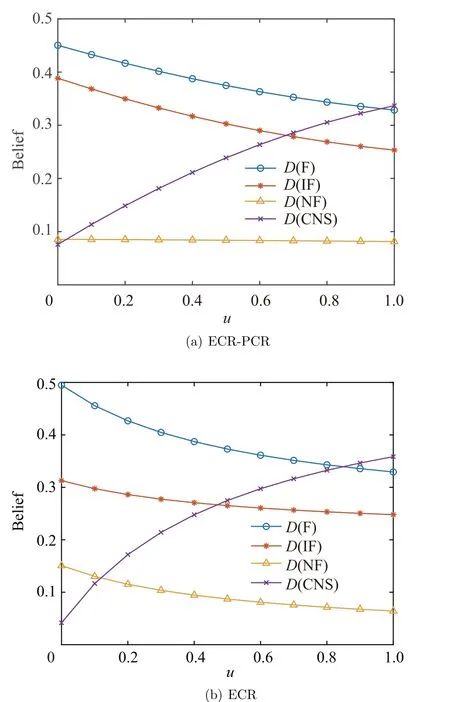
Fig.5 Combination results with change of u by using ECR-PCR and ECR rules in Case 1.

Table 10 Combination results using ECR, PCR and ECR-PCR rules in Case 2.

The ECR, PCR and ECR-PCR rules are used to combine the above D numbers, and the combination results obtained by these rules are given in Table 10.

From Table 10, the beliefs of CNS obtained by the ECRPCR and ECR rules under the same conditions are all lower than those obtained by the PCR rule. Therefore, even if there is a link failure, ECR and ECR-PCR rules are more effective than PCR rule for the forest fire estimation decision-making.

Furthermore, a series of combined results by ECR and ECR-PCR rules is given in Fig.6,both of which continuously change with the non-exclusive degree u.

Fig.6 Combination results with change of u by using ECR-PCR and ECR rules in Case 2.

It can be observed from Fig. 6 that in the results of both ECR-PCR and ECR rules, the belief of CNS increases with the rise of u. Regardless of the value of u, the order of singletons is always D（F ）＞D（IF ）＞D（NF ）, except for u=0 in ECR rule. Thus, in this case, F (Fire) is the most probable result in fire estimation.

6. Conclusions

In this paper, the combination of evidence defined on a nonexclusive FOD has been studied. A novel method called ECR-PCR rule is proposed, by integrating the ideas from PCR rule in DSmT and ECR rule in DNT.The new rule inherits the advantages of ECR rule in quantifying the nonexclusive degrees and PCR rule in redistributing conflict. The effectiveness of the proposed ECR-PCR rule is verified through a wide variety of examples. As a way of example,the proposed rule is used in an application of forest fire detection,which further shows its reasonability and effectiveness in solving real-world problems. At present, the proposed ECRPCR rule cannot be used to combine multiple evidences simultaneously, since it does not satisfy the associativity. In future work, it is worthwhile to construct a general method to combine multiple evidences defined on a non-exclusive FOD on the basis of the idea of ECR-PCR rule.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The work was partially supported by the National Natural Science Foundation of China (No. 61703338).