Fractional order adaptive robust formation control of multiple quad-rotor UAVs with parametric uncertainties and wind disturbances

Environmentl Assessment nd Technology for Hzrdous Wste Mngement Reserch Center, Fculty of Environmentl Mngement, Prince of Songkl University, Songkhl 90112, Thilnd

b Department of Electrical Engineering, College of Engineering Taif University, Al-Hawiyah, Taif P.O Box: 888, Kingdom of Saudi Arabia

c School of Mechanical and Manufacturing Engineering, NUST, Islamabad 44000 Pakistan

d School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China

e Faculty of Environmental Management, Prince of Songkla University, Songkla, 90112, Thailand

KEYWORDS Adaptive robust control;Fractional order control;Nonlinear control;Quad-rotor UAVs;Swarm formation control

Abstract In recent times,multiple Unmanned Aerial Vehicles(UAVs)are being widely utilized in several areas of applications such as agriculture,surveillance,disaster management,search and rescue operations.Degree of robustness of applied control schemes determines how accurate a swarm of UAVs accomplish group tasks. Formation and trajectory tracking controllers are required for the swarm of multiple UAVs. Factors like external environmental effects, parametric uncertainties and wind gusts make the controller design process as a challenging task.This article proposes fractional order formation and trajectory tacking controllers for multiple quad-rotors using Super Twisting Sliding Mode Control(STSMC)technique.To compensate the effects of the disturbances due to parametric uncertainties and wind gusts, Lyapunov function based adaptive controllers are formulated. Moreover, Lyapunov theorem is used to guarantee the stability of the proposed controllers. Three types of controllers, namely fixed gain STSMC and fractional order Adaptive Super Twisting Sliding Mode Control (ASTSMC) methods are tested for the swarm of UAVs by performing the numerical simulations in MATLAB/Simulink environment. From the presented results, it is verified that in presence of wind disturbances and parametric uncertainties, the proposed fractional order ASTSMC technique showed improved robustness as compared to the fixed gain STSMC and integer order ASTSMC.

1. Introduction

A flight in which two or more quad-rotors UAVs travel and maneuver together in a disciplined and synchronized manner is called formation flight. In recent years, formation control of multiple quad-rotors is an emerging research area. UAVs swarm is widely utilized in several industrial applications such as defense sector, aerospace industry, aerial photography, rescue activities, oil field tracking, agriculture, and suspended load transportation.Thanks to its anticipated utility,the payload market size of global UAVs is projected to hit 3 billion$by 2027.As compared to a single UAV, multiple UAVs increase the potential for sensor deployment,payload capacity and surveillance area.However,in presence of uncertainties and disturbances, the formation control problem of multiple UAVs is a challenging task. In addition, another challenging task is the accurate formulation of nonlinear dynamic model for the formation control of multiple quad-rotor UAVs. The rotational and translational dynamics of quad-rotor UAV is modeled as six degree of freedom nonlinear differential equations.For performing group tasks, multiple quad-rotors can have different types of formation geometries which depend on the flight mission and total number of UAVs. The most widely utilized geometries are V-shaped and four-finger configuration.

Many research efforts have been made to solve the quadrotors formation control problem.In Ref.,a leader-follower formation control is proposed by using a classical Proportional Derivative (PD) control scheme and a fuzzy logic system. The proposed method in Ref.is simple to implement however system uncertainties and disturbances are not incorporated in the controller design. A prescribed output controller is proposed in Ref.for swarm of multiple UAVs with guaranteed stable formation pattern. A Proportional Integral Derivative(PID) control integrated method with Sliding Mode Control(SMC) technique is presented in Ref.. The proposed PIDSMC control method of Ref.is robust against external upper bounded disturbances; however, the design process ignores communication delays between quad-rotor UAVs. Classical SMC formation controllers are reported in Refs.,however the inherent high frequency chattering limits practical implementation of such controllers. Moreover, the high frequency chattering in the control excitation signals can shorten the life cycle of the actuators.For circular geometry formation of multiple quad-rotors a control strategy based on classical method is proposed in Ref..A synchronization control method based on classical Proportional Integral(PI)controller is proposed in Ref.for the swarm formation of two quad-rotors. To compensate the communication delays between multiple quadrotors, a distributed controller is presented in Ref.. The above cited literature is focused on the application of classical control methods for the swarm formation of multiple UAVs.Although classical control schemes are easy to implement,however such methods are not robust enough to parameters uncertainties and external disturbances. To address the shortcomings of classical control methods, several nonlinear control methods are applied for the swarm formation of multiple UAVs. A nonlinear distributed controller is presented in Ref.for swarm formation problem of multiple micro-UAVs.Similarly, a cohesive formation controller is reported for trajectory control of multiple quad-rotors in Ref.. For systems with nonlinear coupled dynamics, backstepping control method is the most widely utilized scheme. In Ref., a backstepping controller is reported for the formation of swarm of multiple UAVs. Most of the cited nonlinear control methods above are fixed gain, thus external disturbance and uncertainties can affect the robustness of the control schemes. To address the shortcomings of fixed gain nonlinear control methods,several adaptive control schemes are reported in the literature. In Refs., an adaptive Model Predictive Controller(MPC) is reported for the swarm of multiple quad-rotors.MPC controllers are easy to implement, however it suffers from under and over estimation problem. A novel prioribounded intermediary adaptive control technique is used for robust tracking of velocity and formation control of multiple quad-rotors in Ref..Controlling formation flight of multiple UAVs is even more challenging, when multiple UAVs transport slung load. In order to control the formation flight of multiple quad-rotor UAVs with attached slung load, a guidance algorithm based on the Lyapunov function is proposed in Refs.. A collision avoidance algorithm for leader follower configuration of multiple UAVs is proposed in Ref..In Ref., Lyapunov function based adaptive laws are formulated for compensation of unknown external disturbances affecting the formation flight of multiple UAVs. Similarly, a model reference adaptive control technique is proposed for controlling swarm of three quad-rotor UAVs in Ref.. In the reported work Ref., controller gains are tuned online.The adaptive control schemes presented in Refs.may suffer from under and overestimation problem if the main feedback controllers are not optimally tuned.

To address the shortcomings of integer order adaptive control methods cited above,fractional order control methods are introduced.Several interesting applications of fractional order controllers have been reported in the existent literature,such as fractional order reaching law based robust controller for a quad-rotor in Ref., a distributed fractional order controller for multiple UAVs in Ref., fractional order adaptive neural synchronization control for swarm of UAVs in Ref.and a fractional order pitch loop controller in Ref.. The controller presented in Ref.is applied to a single UAV.The propose of distributed fractional order control scheme in Ref.is focused on establishing finite time information sharing between multiple UAVs,however disturbances like wind gust and parametric uncertainties have not been taken into consideration.The controller presented in Ref.,is more complex due to the integration of adaptive neural networks with fractional order control.Moreover, the control method presented in Ref., is only applied to the pitch loop of the Vertical Take-Off and Landing(VTOL) UAV. Basic definitions of fractional order calculus are elaborated in Ref.. Similarly fractional order fault tolerant control methods are proposed for swarm of multiple UAVs in Refs.. A second order sliding mode control scheme is proposed in Ref..Several adaptive fractional order controllers combined with artificial neural network system have been reported in Refs..Moreover,the computational complexity of such controllers has been addressed in Ref..In order to address chattering problem, control strategies with fixed finite time convergence property are reported in Refs.. A novel robust control scheme is introduced in Ref.for compensation of measurement time delays and external disturbances. Similarly, synchronization problem of uncertain chaotic system is addressed using adaptive terminal sliding mode control scheme in Ref..The specific application of fractional order controllers for formation control of multiple UAVs is still limited and it needs further exploitations.Especially the inherent advantages of the fractional controllers, such as its higher degree of freedom to adjust system performance and its robustness to noise and measurement noise can lead to interesting results when applied to swarm UAVs.

Forgoing in view, the above cited literature rarely exploits fractional order controllers for swarm formation of multiple quad-rotor UAVs.More importantly,the integer order adaptive robust controllers suffer from over and underestimation problem of the uncertainty. The aforementioned problem is addressed using fractional order adaptive super twisting sliding mode control scheme. The hybrid control scheme enables the designers to exploit the inherent advantages of both super twisting algorithm and fractional calculus. Fractional order controllers add extra degree of freedom to adjust system response,thus transient and steady state errors are very close to zero,so the adaptive over and underestimation problems are solved.The specific contributions made in this article are as follows:

(1) In the existent literature, fractional calculus is rarely applied to the swarm formation control problem of multiple UAVs.This article introduces fractional order sliding manifold to derive adaptive super twisting sliding mode controllers for swarm formation of multiple UAVs under wind disturbances and parameter uncertainties.

(2) The proposed adaptive fractional order controllers incorporate the combined advantages of the super twisting sliding mode algorithm and fractional order calculus. The proposed fractional order controller adds extra degree of freedom for fine tuning the system response.

(3) The adaptive laws integrated with integer order controllers suffer from over and under estimation problem.This issue is resolved using fractional order adaptive control method. From the simulated results and in the time intervals when system uncertainty is zero, the estimated term Dwith the proposed fractional order controller is close to zero, while with integer order controller, significant estimation error is observed in the time intervals when system uncertainty is zero.

Rest of the paper is divided into four parts.System description and mathematical model is discussed in Section 2.Section 3 formulates the propose controller.Section 4 presents simulation results.Finally,in Section 5,conclusions are made.

2. System description and mathematical modeling

Dynamics of quad-rotor UAV in earth’s frame of reference(X,Y, Z) are depicted in Fig. 1. (X, Y, Z) represents the body coordinates of the quad-rotor. To derive quad-rotor model,the following assumptions are introduced:

Assumption 1.A quad-rotor is represented by a symmetrical rigid body configuration with mass m.

Assumption 2. The wind gust affects X, Y and Z dynamics of each UAV.

The dynamic model equations of a quad-rotor are formulated in Eqs. (1)-(6). In these equations, the uncertainty in X and Y dynamics of a UAV is represented by Dand D. Here, i represent [L，j] and j ∈{F1，F2}, where the leader UAV is represented by the subscript L,while follower UAVs is represented by F1 and F2 respectively. Referring to Fig. 2(a),the formation dynamics of multiple UAVs are expressed by Eqs. (7)-(9):

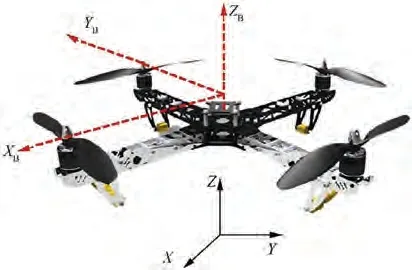
Fig. 1 Quad-rotor in inertial reference frame.

Fig. 2 Swarm Configuration and Control Block Diagram.

3. Trajectory and formation controller’s formulation

In this section fractional order attitude, altitude and position controllers are formulated for the leader UAV as a first step.Then in the second step, the formation controller is derived to calculate the new references for follower UAVs.The trajectory and attitude controllers derived for leader UAV are then generalized for follower UAVs in the last step. Following assumptions are introduced before formulating the control schemes:

Assumption 4.For the uncertainty terms,the following conditions holds true:

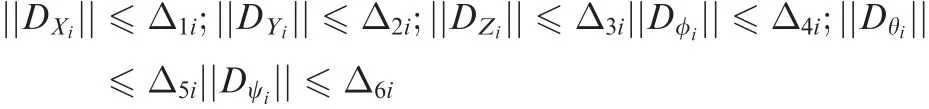
where the upper limits of the above uncertainties are represented by Δ，Δ，Δ，Δ，Δ，Δ.Appendix A shows basic definitions of fractional calculus required for the formulation of the proposed control schemes.

3.1. Leader UAV

In this subsection,fractional order super twisting sliding mode control method is used to derive the attitude,altitude and position controllers for the leader UAV.

3.1.1. Fractional order attitude control

Attitude controller regulates roll, pitch and yaw angles of a quad-rotor. Let φ，θψrepresent the reference Euler angles of leader quad-rotor, then sliding surface for the roll angle is defined as follows:

3.1.2. Fractional order altitude and position controllers

In this section, fractional order altitude and position controllers are formulated for leader UAV.The altitude controller is formulated first and then by using the transformation matrix, the position controllers are derived. With the desired altitude Z， the sliding manifold is defined as follows:

Note. The proposed fractional order sliding surfaces given by Eqs. (19), (31) and (40) contain fractional integral and derivative terms of the respective error terms. In order to implement the proposed fractional order sliding surfaces,fractional operator α must fulfill the following criteria:0 ＜α ＜0.5.

3.2. Leader follower formation control

Before derivation of the trajectory controllers for the follower UAVs, we need to figure out how to calculate the formation controller to produce the reference trajectories for the follower UAVs. The sliding manifold for the formation controller is defined as follows:

3.3. Follower UAVs control formulation

In this section, the trajectory tracking controllers of follower UAVs are briefly introduced. The reference position trajectories, as previously stated, are formed using Eq. (18) and are controlled by the formation controller of Eq. (57). By specifying the errors for the attitude, altitude, and position loops of follower UAVs’, the rest of the procedures required to derive the subject controllers are very similar as of the leader UAV.The final control laws are directly expressed below for the purpose of simplicity. The sliding manifolds for the attitude controllers are defined as follows:

where the parameters of sliding surfaces for follower UAVs are represented by k，k，k，k，k，k. The error terms are defined as follows: e=Z-Z;e=X-Xe=Y-Y. Now, the attitude, altitude and position con-trollers for follower UAVs are formulated by following the same procedures as above.

Table 1 Leader-follower UAVs design parameters.

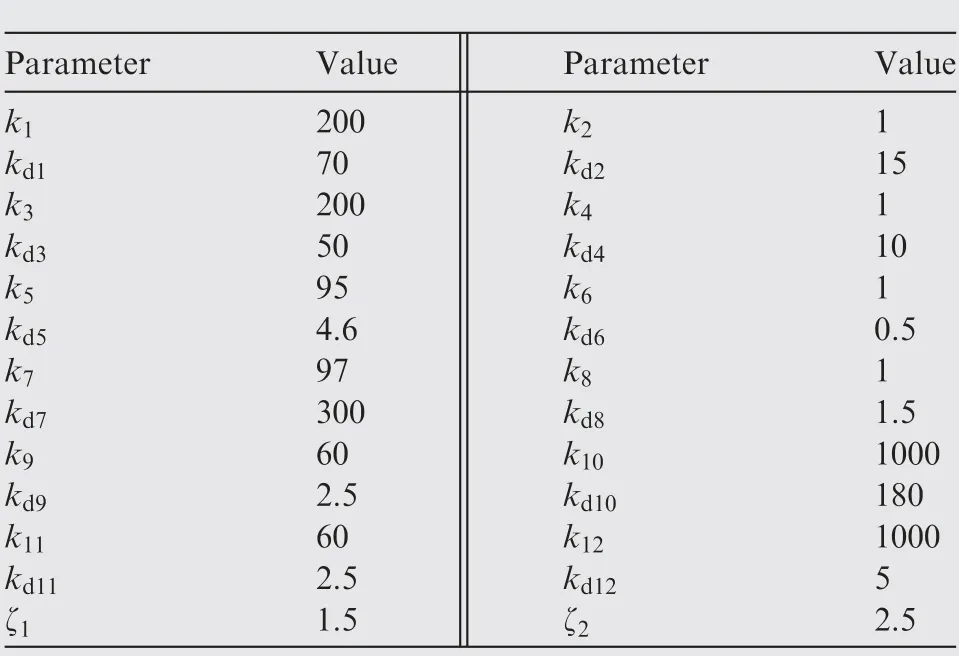
Table 2 Leader UAV controls parameters for attitude,altitude and position loops.

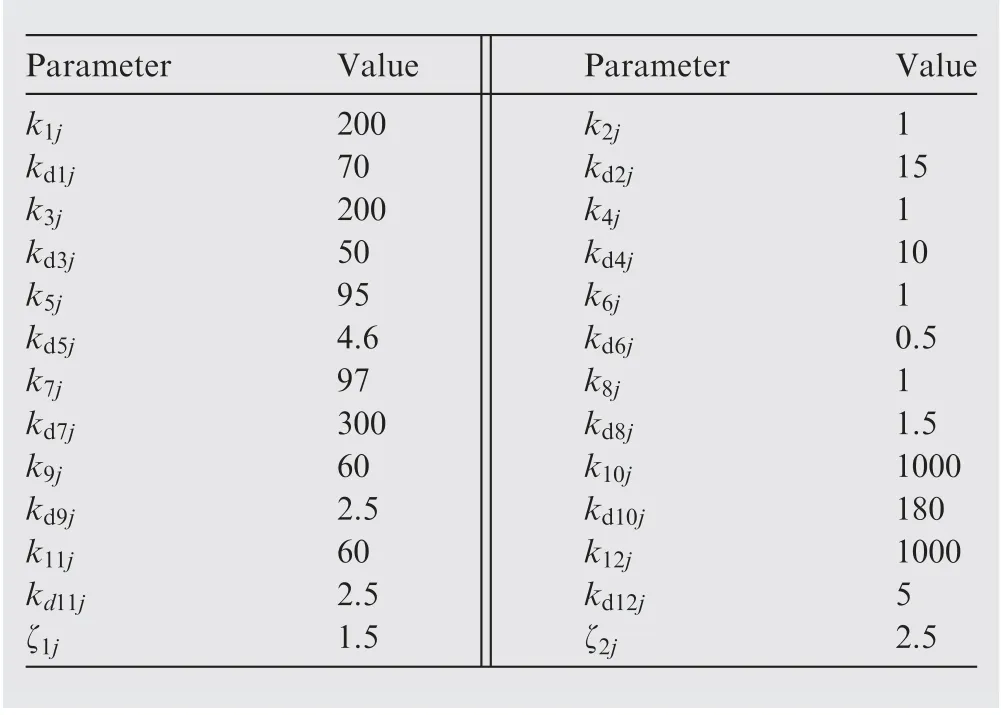
Table 3 Follower UAVs control parameters for attitude,altitude and position loops.

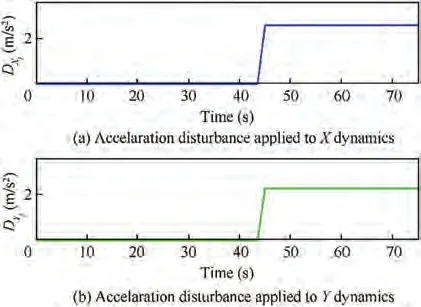
Fig. 3 Applied acceleration type disturbance in X and Y loops.

Fig. 4 3D trajectory tracking.

Fig. 5 X-Y leader trajectory tracking under parameter uncertainty and wind disturbance.

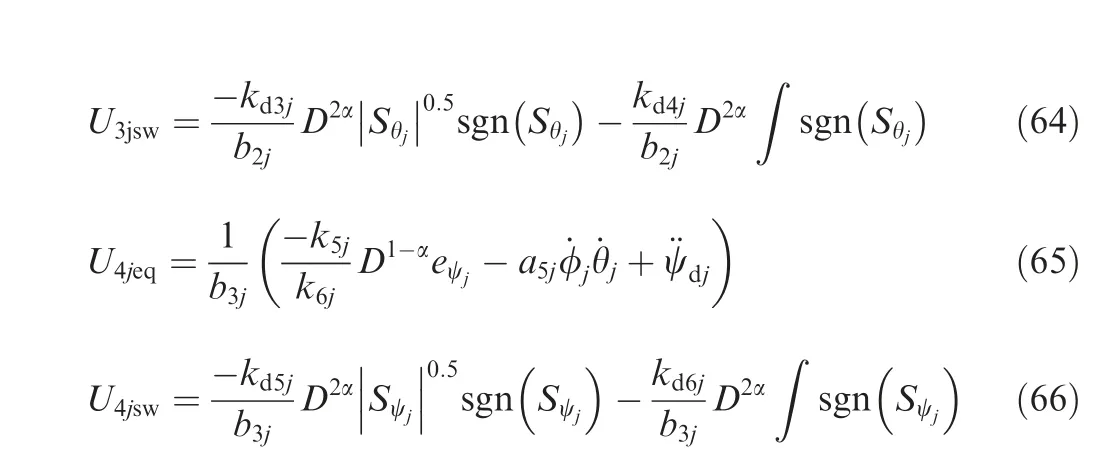
Fig. 6 X-Y Follower 1 trajectory tracking under parameter uncertainty and wind disturbance.

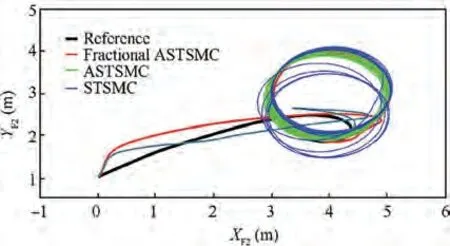
Fig. 7 X-Y Follower 2 trajectory tracking under parameter uncertainty and wind disturbance.

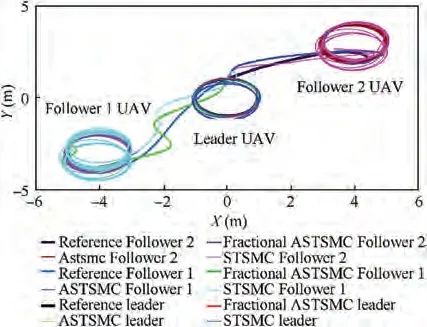
Fig.8 X-Y trajectory tracking under parameter uncertainty and wind disturbance.

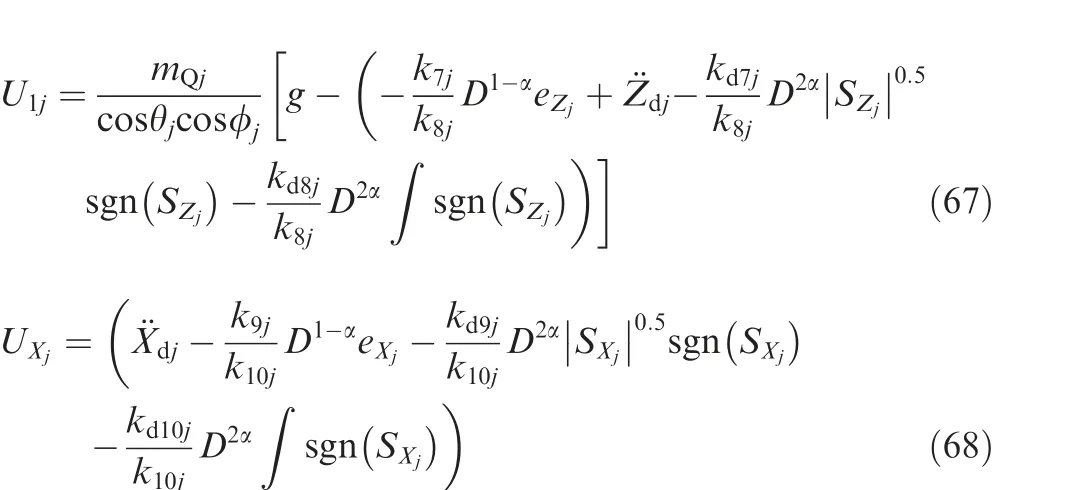
Fig. 9 XL tracking comparison under wind disturbance.

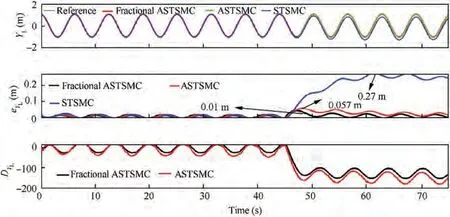
Fig. 10 YL tracking comparison under wind disturbance.

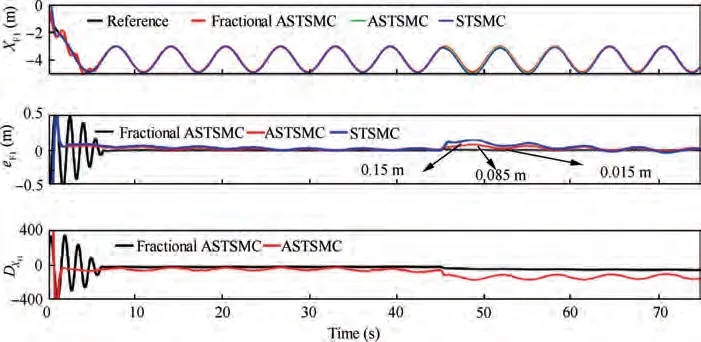
Fig. 11 XF1 tracking comparison under wind disturbance.

Fig. 12 YF1 tracking comparison under wind disturbance.

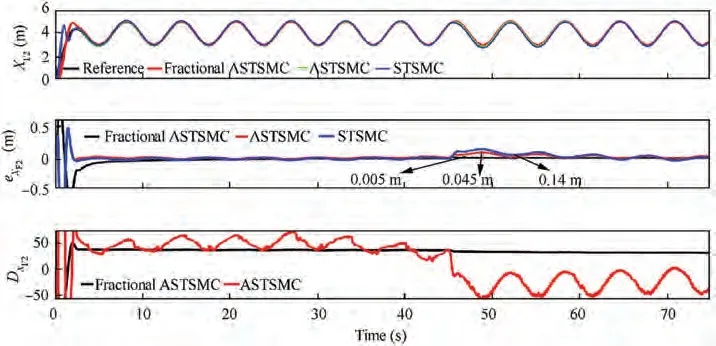
Fig. 13 XF2 tracking comparison under wind disturbance.

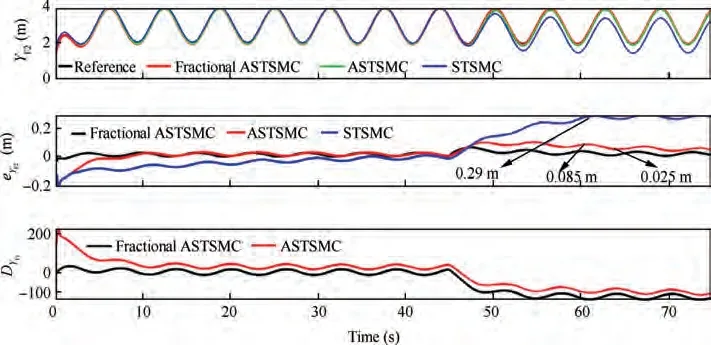
Fig. 14 YF2 tracking comparison under wind disturbance.

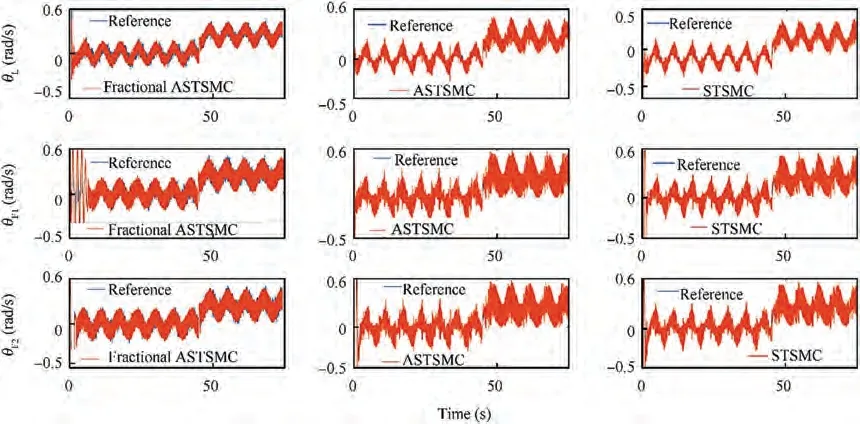
Fig. 15 θ tracking comparison under wind disturbance.

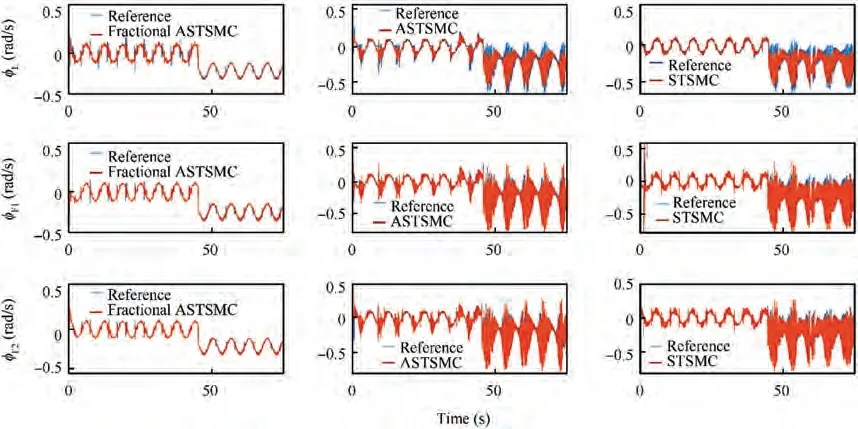
Fig. 16 φ tracking comparison under parametric uncertainties and wind disturbance.

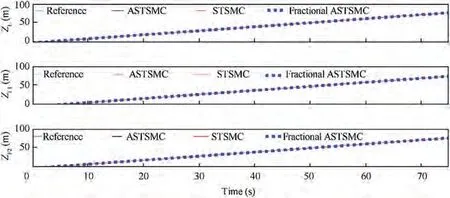
Fig. 17 Z tracking comparison under parametric uncertainties and wind disturbance.

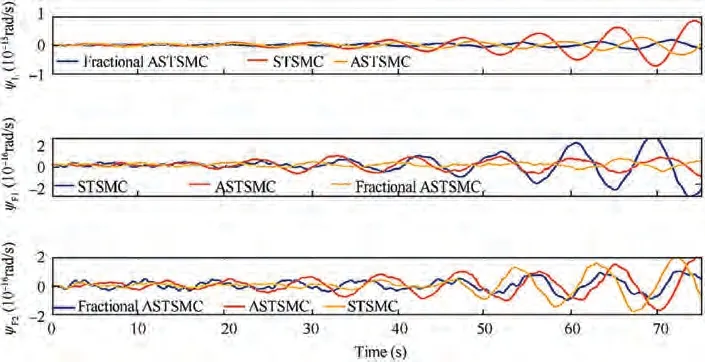
Fig. 18 ψ tracking comparison under parametric uncertainties and wind disturbance.

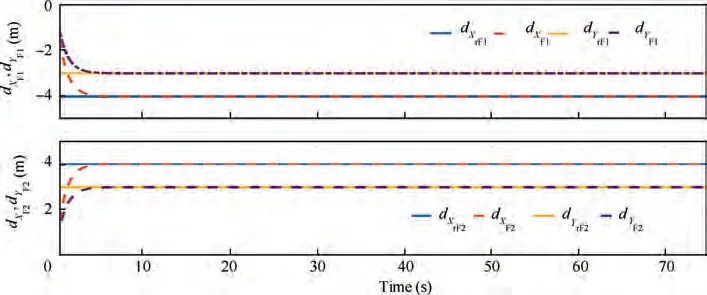
Fig. 19 Formation controller tracking.

Remark 2. The proposed fractional order controllers given in Eqs. (22)-(27), (32), (42) and (61)-(69) exploit the inherent advantages of super twisting algorithm and fractional order calculus. The proposed schemes consist of fractional order terms Dein equivalent control parts and thus with extra degree of freedom i.e. (fractional operator), it offers more flexibility to adjust system control performance. Similarly, the robust parts of the proposed control schemes also include fractional derivative terms Dthat also add extra degree of freedom to adjust fractional derivative and integration of the discontinuous signum functions.MATLAB parameter estimation toolbox is utilized to choose the best parameters for a known set of trajectories. Nonlinear least square search method is used to get the optimal control parameters.Moreover, Oustaloup approximation method is used for numerical implementation of fractional operator.

4. Results and discussion

Fig.4 depicts the 3D simulations for the trajectory tracking of leader and follower quad-rotors in the presence of the applied disturbances.The results show that fractional and integer order ASTSMC controllers provide robust behavior in the presence of disturbances, however with fixed gain STSMC algorithm, significant steady state errors in the longitudinal and lateral dynamics of the leader and follower UAVs are observed.

The X-Y trajectory tracking comparisons for the leader and follower quad-rotors are illustrated in Figs.5-8.The presented results show that all UAVs with fractional ASTSMC algorithm have the smallest deviations in trajectory tracking,while ASTSMC has the largest errors when compared to the proposed fractional order schemes. Furthermore, there is a considerable drift from the desired trajectories in the X-Y plane of all the UAVs when using fixed gain STSMC. Fig. 8 depicts the combined trajectories of leader-follower UAVs with fractional order ASTSMC,ASTMSC and fixed gain STSMC techniques. The proposed fractional order ASTSMC controllers offer robust formation control between the leader and follower UAVs, whereas in fixed gain STSMC technique, all the quad-rotors show drift in their trajectories. While with ASTSMC controllers, the trajectory deviations are larger as compared to the proposed fractional order ASTSMC controllers.

The X and Y trajectories are separately plotted against time for the comparison of the trajectory tracking performance of the leader-follower UAVs quantitatively, and the results are displayed in Figs. 9 and 10 for the leader UAV. From Fig. 9, and at time t=45 s， etrajectory tracking error is 0.105 m with fixed gain STSMC technique while with fractional order ASTSMC and ASTSMC schemes, the measured error eis 0.045 and 0.001 m respectively. Both fractional order ASTSMC and ASTSMC based control laws ensure lowest errors because of the adaptive disturbance compensation term Dand from the results presented in Fig.9,it is obvious that at time t=45 s, the adaptive term Dadds appropriate compensation term to cancel the disturbance and it switches from 0 to-50 in case of fractional order ASTSMC while with ASTSMC it changes from 50 to -50. Similarly, from Fig. 10,eis calculated as 0.27 m,0.057 m and 0.01 m with fixed gain STSMC, ASTSMC and fractional order ASTSMC schemes respectively. Both fractional order ASTSMC and ASTSMC offer lowest error due to the adaptive estimator term D.From the presented results of Fig.10,it is clear that the adaptive term Dadds appropriate compensation control to cancel the disturbance at time t=45 s,and it switches from 0 to-120 in case of fractional order ASTSMC while with ASTSMC it switches from 0 to -150. Moreover, the adaptive compensation terms with ASTSMC based control law suffer from over and under estimation problem, while the proposed fractional order ASTSMC scheme adds appropriate compensation without over and under estimation problems. Similarly, for follower UAVs, the X and Y tracking responses are plotted against simulation time and the results are shown in Figs. 11-14. From the results displayed and at time t=45 s,the measured error with fixed gain STSMC control method is as follows: e=0.15 m，e=0.269 m，e=0.14 m，e=0.29 m， while with ASTSMC based law, the errors are measured as follows: e=0.085 m，e=0.069 m，e=0.045 m, e=0.085 m. While with the proposed fractional order ASTSMC scheme,lowest errors magnitude are recorded:e=0.015 m，e=0.01 m，e=0.05 m, e=0.025 m.From the presented results of Fig. 11- 14， it is obvious that at time t=45 s, the adaptiveterms D，D，DDadd appropriate compensation control to cancel the effects of disturbances.The results presented in Figs.15 and 16 show θ and φ tracking responses for leader and follower UAVs with the discussed three variants of the control schemes. From the presented results and at time t=45 s, it is evident that the proposed fractional order ASTSMC schemes generate smooth reference commands for both θ and φ loops of leader and follower UAVs, while with ASTSMC and STSMC schemes, θ and φ tracking suffers from oscillations.

The results presented in Figs. 17-19 show Z, ψ and formation tracking responses for leader-follower quad-rotors under the action of discussed control schemes. From the presented results of Z and ψ loops, it is obvious that the tracking response is similar for all the controllers. The reason is very obvious because the parametric uncertainty is well compensated by all three variants of controllers.Fig.19 shows the formation tracking response between the leader and follower UAVs, and from the results presented, it is obvious that a robust formation control is ensured by the proposed controller.

5. Conclusions

This paper presents a fractional order ASTSMC technique for the trajectory and formation control of swarm of quad-rotors in a leader-follower formation. Wind disturbances and parametric uncertainties are applied to the longitudinal and lateral dynamics of the leader and follower quad-rotors. Swarm formation control of quad-rotors is simulated with the proposed fractional order ASTSMC, ASTSMC and fixed gain STSMC schemes. From the presented results, it is concluded that in comparison to the fixed gain STSMC, the proposed fractional order ASTSMC and ASTSMC schemes adaptively compensate the disturbances and the formation of leader-follower UAVs follows the reference formation with minimum errors in the trajectories of all UAVs. Moreover, it is further concluded that the adaptive loops with ASTSMC controllers suffer from under estimation and over estimation problems,while with the proposed control scheme the mentioned problem is rectified using fractional calculus and thus the errors in system trajectories are minimum.

6. Future recommendations

From Section 5,it is concluded that under the effect of external disturbances and system uncertainties,the proposed fractional order trajectory and formation controllers exhibited enhanced robust performance in comparison to integer order ASTSMC and fixed gain STSMC methods. In practice, fractional order controllers utilize more computational resources as compared to integer order controllers of the same family.To reduce the implementation complexity of the proposed fractional order control methods, the idea presented in Ref.can be exploited further in the future research studies for multiple UAVs swarm formation problem.

This research was supported by Prince of Songkla University and the Ministry of Higher Education, Science, Research and Innovation, under the Reinventing University Project(No. REV64022).

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Authors acknowledge the funding support of Prince of Songkla University and the Ministry of Higher Education,Science, Research and Innovation, Thailand, under the Reinventing University Project (No. REV64022).

Riemann Liouville (RL), Caputo and Gru¨nwald-Letnikov definitions are usually utilized to approximate fractional operator. RL fractional integral is defined as follows