高温翅片管的长时蠕变屈曲分析及评定方法研究
张 瀛,邝临源,姜 露,杜 娟,刘贞谷
(中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610213)
相较于第三代压水堆,第四代反应堆为提高经济性,其设计运行温度往往更高。换热管是反应堆换热器的重要换热元件,翅片管是在传热管的表面通过设置翅片、增大表面积,从而达到提高换热效率目的的一种换热管。由于其承受外压载荷,需考虑其发生屈曲失效的风险,而在高温的环境下,屈曲失效需同时考虑瞬时屈曲(与时间无关的屈曲)和蠕变屈曲(与时间有关的屈曲)。
瞬时屈曲可能在寿期内的任意时间瞬间发生,只取决于几何结构和在时间上的短时材料响应,与时间无关。在ASME规范[1]、RCC-M规范[2]、RCC-MRx规范[3]、API[4]以及中国国家标准[5]中都有各自的分析和评定方法。
蠕变屈曲从某种意义上说,是弹塑性失稳问题的一种扩展,但也不再是经典意义上的稳定性问题。蠕变屈曲是因为初始缺陷随时间而放大,从而导致几何失稳,这种失效与时间有关,因此在蠕变屈曲研究和设计中,需评定的是发生最终失稳的临界时间是否大于结构的设计寿命。由于蠕变应变随时间进行累积,发生蠕变屈曲时的载荷小于发生瞬时屈曲的载荷。ASME NH中仅给出了各工况下的蠕变屈曲载荷系数,但因对蠕变屈曲这一复杂现象研究尚不充分,一些研究成果不便应用,故ASME尚未推荐出一种专门的分析方法应用于工程,即未能规定如何计算屈曲失稳的临界时间。RCC-MRx规范附录A7提供了一种蠕变屈曲简化设计方法,可用于薄壳结构的蠕变屈曲设计,但该方法仅适用于高温持续时间不超过10 000 h、温度低于700 ℃的不锈钢材料。
国外蠕变屈曲的研究始于20世纪40年代。结构蠕变屈曲的研究首先从简单的杆件或柱状结构开始,继而发展到板、壳的蠕变屈曲。Shanley等[6]假设结构是无初始缺陷的,将经典稳定性理论中的准则引至蠕变屈曲,从而确定出蠕变屈曲临界时间。Obrecht[7]研究了圆柱壳体结构在轴压载荷作用下的蠕变屈曲分析方法。Combescure[8]研究了壳体结构在外压载荷作用下的蠕变屈曲临界时间预测方法,并通过试验给予了验证。Hoff等[9]假定圆柱壳截面具有初始及发展的两波形偏差,并假设材料服从Norton稳态蠕变定律,求得无限长圆柱壳外压蠕变的屈曲解。严爱民等[10]在Hoff等[9]的理论模型基础上,通过构造M波力学模型进行解析,获得了有限长圆柱壳的外压蠕变屈曲解,进行了蠕变屈曲实验[11],并对比了理论解和实验结果[12]。Minahen等[13]和Szyszkowski等[14]分别采用不同方法研究了黏弹性结构蠕变失稳准则。
本文对翅片管在高温环境下的蠕变屈曲分析及评定方法进行研究。首先,采用规范中的蠕变屈曲分析方法对结构进行分析及评定。随后,采用有限元法,在恒温恒压的载荷工况下,引入初始几何缺陷、塑性本构和蠕变本构,计算结构的临界屈曲时间,并与规范的方法进行对比,验证有限元法处理蠕变屈曲问题的可行性,为复杂结构和复杂载荷工况的蠕变屈曲分析提供方法上的准备。最后,通过数值拟合,获得压力-时间的失效评定图以及压力-时间-缺陷尺寸的失效评定图,并研究在有压力波动的情况下结构的临界屈曲时间与载荷历程的关系。
1 蠕变屈曲特征
蠕变屈曲不仅涉及几何非线性和材料非线性问题,还对初始缺陷具有敏感性。蠕变屈曲对初始缺陷的敏感程度可通过变形和时间的关系来表示,如图1所示。轴向压缩的圆杆和外压圆柱壳的变形与时间曲线具有代表性。一般来说,任何结构都会有微小的缺陷,在不会导致瞬时屈曲的载荷作用下,由于蠕变影响,初始缺陷会随时间得到放大,这些变形一直增加直到几何结构变得不稳定,如图1中的A点,随后便发生屈曲。
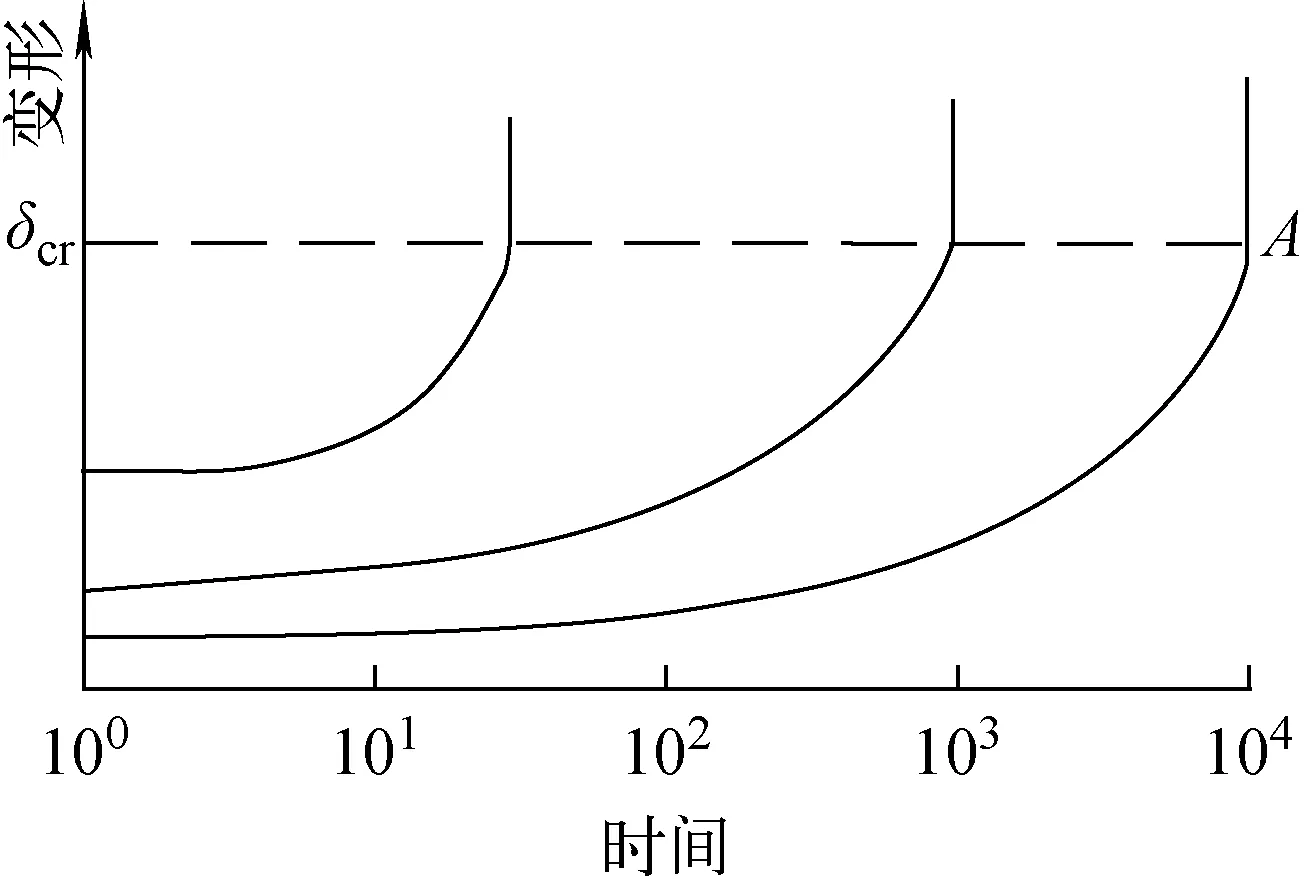
图1 蠕变屈曲变形-时间特征Fig.1 Creep buckling deformation-time characteristic
2 分析对象
本文分析对象为换热器中的翅片管。翅片管的结构形式如图2所示,长度L=1 435 mm,外径D0=22.5 mm,壁厚h=1 mm,直径的最大公差为0.25 mm。材料为316不锈钢,运行外压为1 MPa,运行温度为600 ℃,该温度下弹性模量E=150 GPa,屈服强度Sy=113 MPa。
根据工程经验,图2中的翅片形式对结构的加强作用并不明显,可保守地将翅片管结构简化成相同结构尺寸的圆管结构。
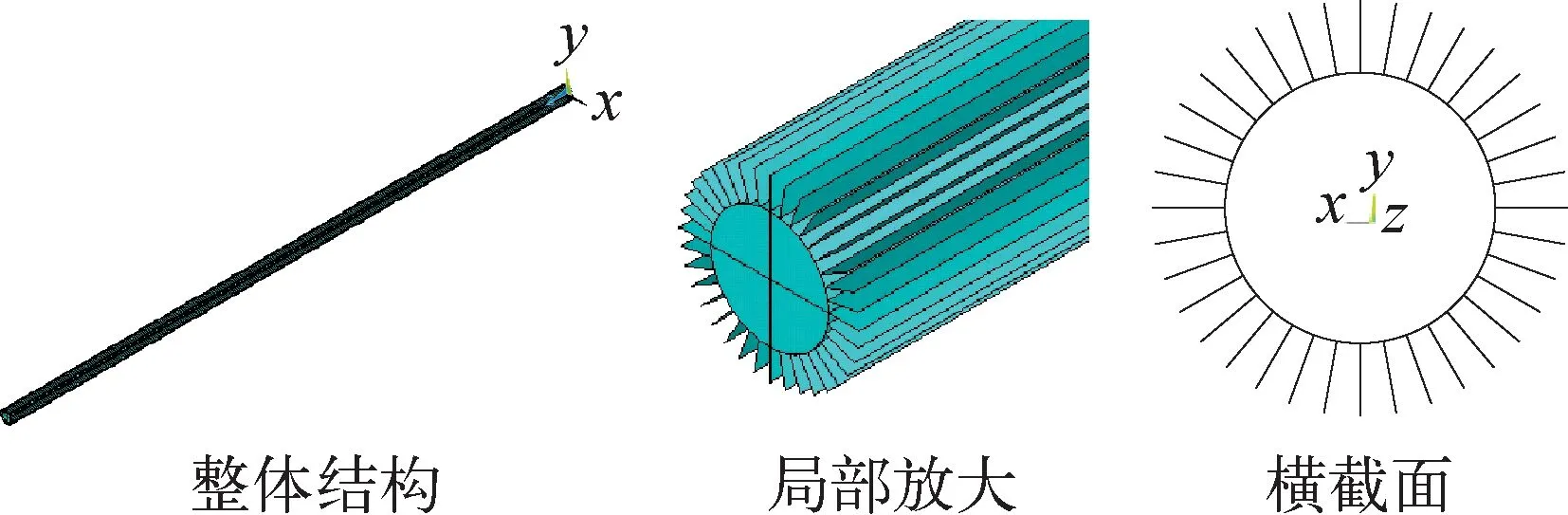
图2 翅片管结构Fig.2 Structure of finned tube
3 蠕变屈曲的规范解法
RCC-MRx附录A7提供了一种蠕变屈曲简化设计方法,可用于薄壳结构的蠕变屈曲设计。该方法根据外压圆环的弹性屈曲理论,假设圆环含正弦型几何缺陷,结合材料的蠕变本构,通过理论推导得出蠕变屈曲控制方程,再将方程绘制成蠕变屈曲设计曲线。但本方法仅适用于高温持续时间不超过10 000 h、温度低于700 ℃的不锈钢材料。分析流程如图3所示,蠕变边界线示于图4,缺陷的几何定义如图5所示,设计曲线示于图6。
根据图3所示分析流程,每步分析结果如下:1) 根据图4的蠕变边界线和本文的输入参数,翅片管需考虑蠕变影响;2) 不考虑几何缺陷,600 ℃工作温度下的弹性屈曲载荷PE=3.07 MPa;3) 采用有限元商业软件ANSYS[15]的结构壳单元对结构进行有限元建模,约束模型底部的所有自由度,在模型的外表面施加1 MPa外压,有限元模型示于图7,计算得到模型中面的应力为10.2 MPa,PL=Sy/10.2×1=113/10.2=11.08 MPa;4)PE/PL=0.277,选择的设计曲线如图6所示;5)x=P/PE=1×1.5/3.07=0.489;6) 缺陷值d=0.25/4=0.062 5 mm,其定义如图5所示,缺陷系数δ=d/h=0.062 5;7) 根据设计曲线,结构在600 ℃温度、0.062 5缺陷系数下,规范解法所得时间(t)为100、1 000、10 000 h时的临界屈曲压力分别为2.27、2.09、1.94 MPa。
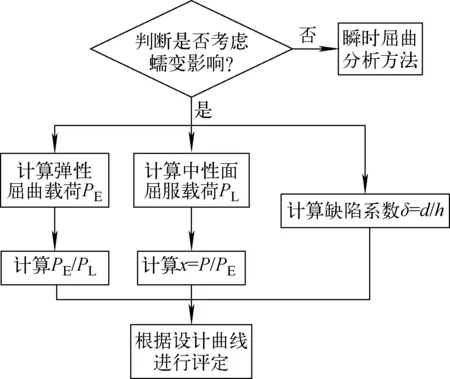
图3 RCC-MRx附录A7的蠕变屈曲分析流程Fig.3 Creep buckling analysis process of RCC-MRx appendix A7
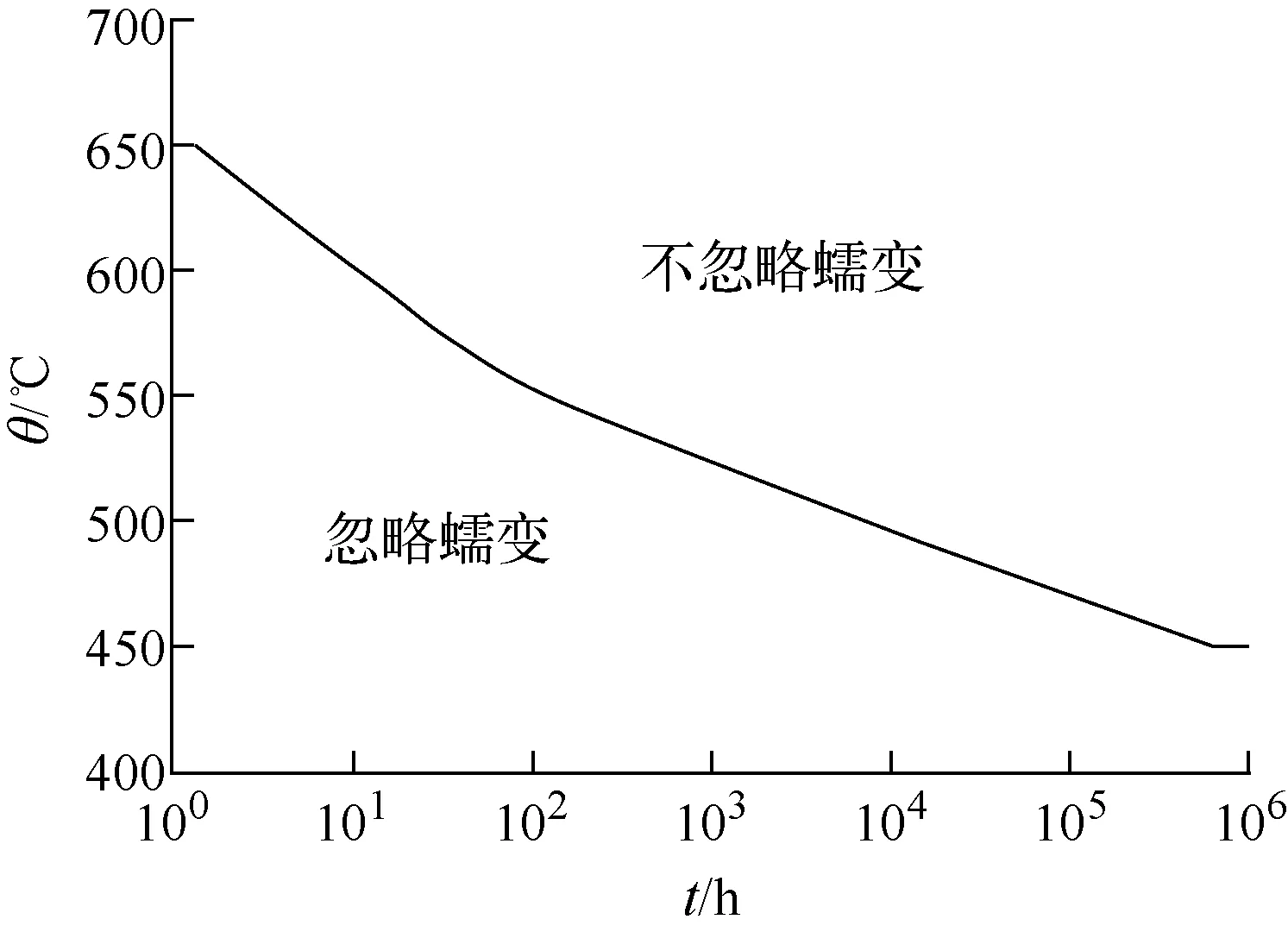
图4 RCC-MRx的蠕变边界线Fig.4 Negligible creep curve of RCC-MRx

图5 修正几何结构的定义Fig.5 Modified geometric definition

图6 RCC-MRx附录A7的蠕变屈曲设计曲线(600 ℃)Fig.6 Buckling diagram at creep at 600 ℃ of RCC-MRx appendix A7

图7 有限元模型Fig.7 Finite element model
4 蠕变屈曲的有限元解法
由于规范解法仅针对简单的结构和载荷,本文采用ANSYS对恒压恒温外压圆柱壳的蠕变屈曲临界时间进行求解,并结合规范解法的分析结果进行对比分析。本文所用蠕变屈曲有限元解法的分析流程如图8所示。
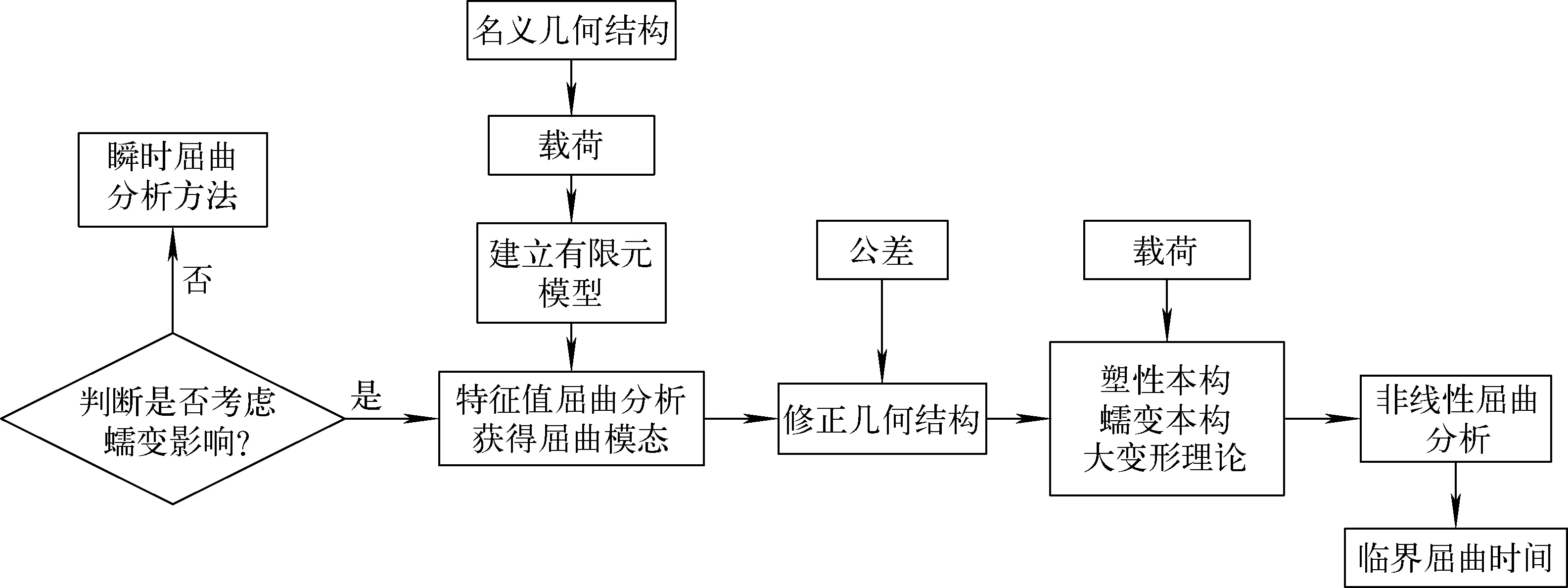
图8 蠕变屈曲有限元解法分析流程Fig.8 Creep buckling analysis process of finite element method
4.1 特征值屈曲分析
通过图4所示蠕变边界线判断结构是否需考虑蠕变影响后,首先根据第2章中的参数,采用名义几何结构进行有限元建模(图7)以及特征值屈曲分析。
特征值屈曲分析预测了理想弹性结构的理论屈曲强度。对于基本结构配置,结构特征值根据约束和载荷条件计算。然后推导屈曲载荷,每一载荷都与一个屈曲模态形状相关,该屈曲模态形状表示结构在屈曲下所假定的形状。在实际结构中,缺陷和非线性行为使结构无法达到这种理论屈曲强度,所以特征值临界屈曲载荷是一上限值。对于工程问题,通常将第1阶屈曲模态所对应的载荷结合1个较大的安全系数作为临界屈曲载荷。
本文对翅片管简化后的圆管进行特征值屈曲分析,结果示于图9。对结构施加外压,通过屈曲模态分析,得到第1阶屈曲模态的屈曲载荷对应的最大变形量为7.243 mm。
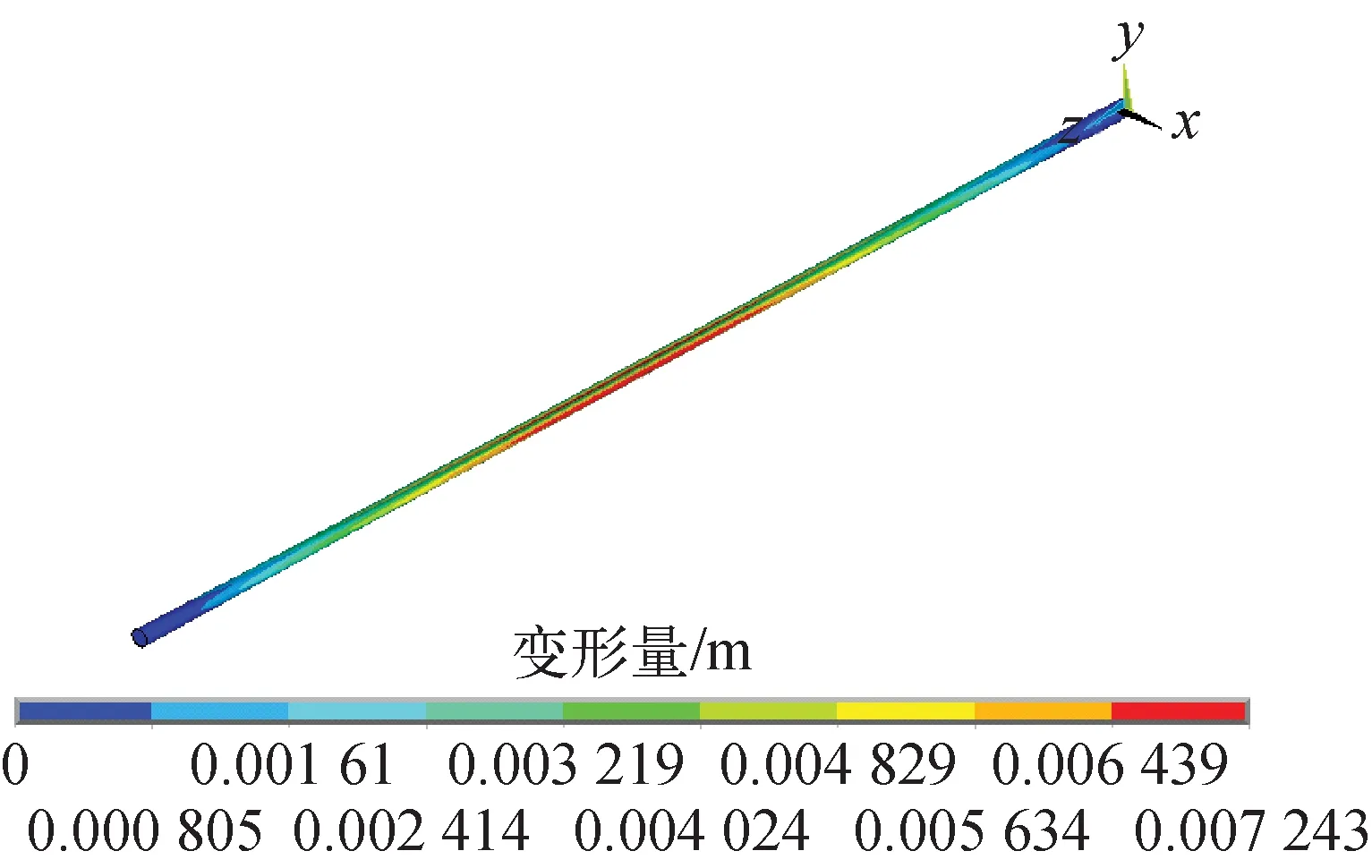
图9 特征值屈曲分析结果Fig.9 Eigenvalue buckling analysis result
4.2 非线性屈曲分析
通过特征值屈曲分析得到结构的初始缺陷后,将该初始缺陷乘以比例系数进行修正,使其与最大公差相匹配,然后将其引入到结构中,并同时考虑材料的塑性本构和蠕变本构,进行非线性屈曲分析。
对于不考虑蠕变影响的非线性屈曲分析是一种考虑材料和几何非线性、载荷扰动、几何缺陷和间隙的静力学方法。逐渐增大施加的载荷,直到载荷水平的微小变化引起位移的大变化,通过有限元的迭代算法,得到解开始变得不稳定前载荷的最大值,即临界屈曲载荷。
在ANSYS中采用多线性的塑性本构,材料的塑性本构模型来源于文献[10],本构关系如下:
其中:σ为应力;C0=1.198、n0=0.112 5为材料的塑性常数;εp为塑性应变。
本文采用的屈服准则为Von Mises屈服准则,其表达式如下:
f(σ,Sy)=σe-Sy=0
其中,σe为等效应力。
对于考虑蠕变影响的非线性屈曲分析,则是对结构施加恒定的载荷(由于基本计算参数及理论本身的误差等,工作载荷需乘以规范中规定的载荷系数,本文采用ASME NH中规定的载荷系数,运行工况下载荷系数为1.5),直到载荷水平的微小变化引起位移的大变化,通过有限元的迭代算法,得到解开始变得不稳定前时间的最大值,即临界屈曲时间。而评定结构是否满足设计要求的依据则取决于临界屈曲时间是否小于设计寿命。
材料的蠕变本构模型来源于文献[3],本构关系如下:
εcr=Kσstq
其中:εcr为蠕变应变;t为时间;K、s、q为材料的蠕变常数,600 ℃下K=8.747 6×10-13、q=0.559 1、s=4.778 5。
由于蠕变的本构方程是非线性的,同时蠕变过程中应力会进行重新分配,蠕变变形量与瞬时应力有关,而瞬时应力又是时间的函数,所以蠕变问题极其复杂。用有限元解法求解蠕变问题的基本思想是:把蠕变经历的时间分成有限间隔,如Δt0,Δt1,…,Δti,求得每一时间间隔的蠕变变形量,将所有时间间隔的蠕变变形量进行求和,即得整个时间历程的蠕变变形量。
ANSYS程序中使用隐式和显式两种方法进行蠕变分析。隐式蠕变应用欧拉向后积分法求解蠕变应变。该方法在数值上无条件稳定,即它不必像显式蠕变方法使用小的时间步,所以整体上更快。由于隐式蠕变较显式蠕变更稳定、精确和高效,因此本文采用该方法进行计算。
在计算第i个时间间隔内的蠕变量时,隐式欧拉法计算首先在1/2≤α<1范围内选定某一数值。在微量时间Δt内,隐式欧拉法的表达式为:
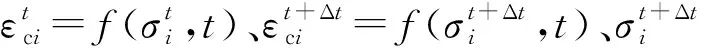
ANSYS提供了一系列蠕变计算公式来模拟材料的蠕变效应,根据材料的蠕变本构的特点选择合适的蠕变模型,在ANSYS提供的隐式蠕变计算公式中选择使用第6个公式,即改进的时间硬化蠕变模型,其具体表达式如下:
根据文献[3]的蠕变本构参数,拟合得到C1=1.07×10-43、C2=4.778 5、C3=-0.440 9。
根据以上参数,计算得到结构在温度600 ℃、缺陷系数0.062 5以及运行压力1 MPa(需乘以载荷系数1.5)下的临界屈曲时间为868 947 h。
为与规范解法的计算结果进行对比,本文计算了多个压力下的临界屈曲时间,并对结果进行拟合,拟合所得结构在温度600 ℃、缺陷系数0.062 5下的失效评定图如图10所示。图10中n2为ASME NH中运行工况下的蠕变屈曲载荷系数,对于常用的奥氏体不锈钢,载荷系数取1.5大致相当于将设计寿命取10的系数;同时,结构还须满足瞬时屈曲的稳定性条件,运行工况下的载荷系数为n1=3;Pins为瞬时屈曲的临界压力,Pcr为蠕变屈曲的临界压力。结合瞬时屈曲与蠕变屈曲的分析结果即可得到失效评定图。
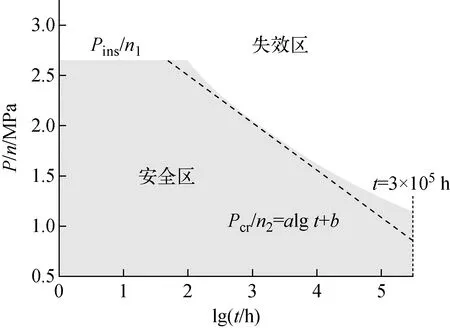
图10 初始缺陷确定的失效评定图Fig.10 Failure assessment diagram with certain initial defect
根据图10可得到有限元法在不同时间下的临界屈曲压力,有限元法与规范法所得结果对比列于表1。
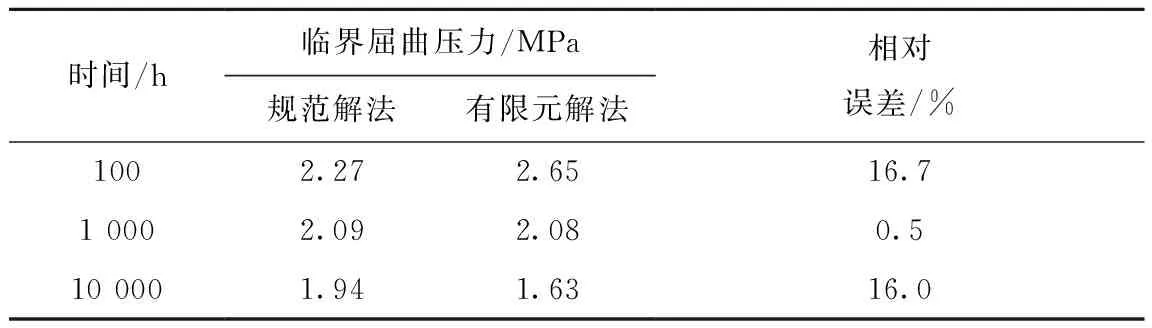
表1 不同时间下的临界屈曲压力Table1 Critical buckling pressures for different durations
由于外压蠕变屈曲是一非常复杂的非线性问题,影响因素众多,因此表1中有限元解法结果与规范解法结果的最大相对误差不超过20%,可认为一致性较好。
在工程中,为更快速地获得临界屈曲载荷或临界屈曲时间,对图10中的结果进行保守拟合,可得到600 ℃、0.062 5下的评定准则:
其中:a=-0.47,b=3.44;Pop为运行压力。
将缺陷系数作为一个不确定的参数时,计算所得压力-时间-缺陷系数的三维失效评定图如图11所示。结构在满足图11所示失效边界的同时,还需满足图12所示瞬时屈曲的失效边界。在工程中,为避免繁琐的迭代计算,应尽可能确定结构、材料等输入参数,然后作蠕变屈曲寿命校核。
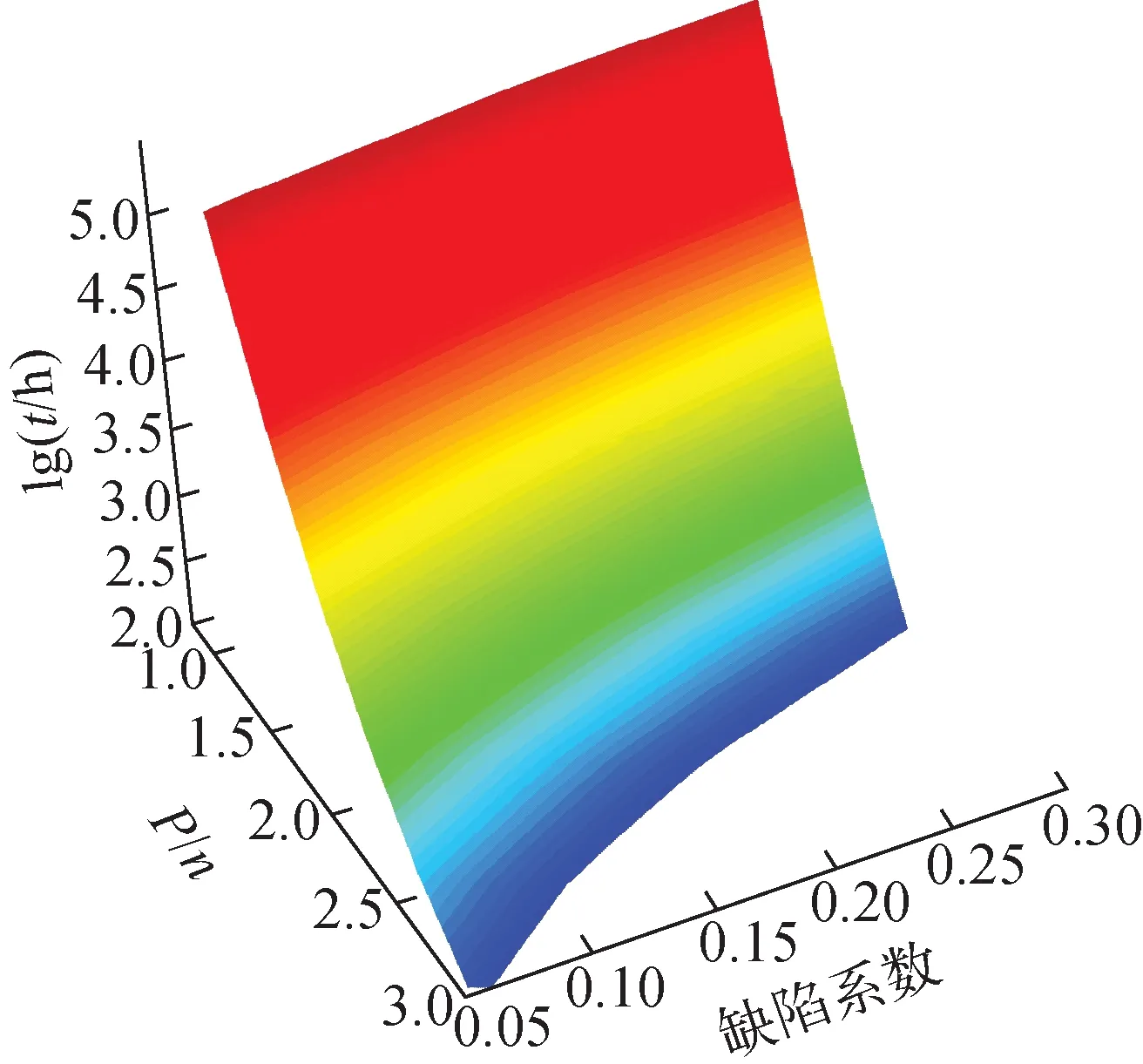
图11 初始缺陷不确定的蠕变屈曲的失效评定图Fig.11 Creep buckling failure assessment diagram with uncertain initial defect
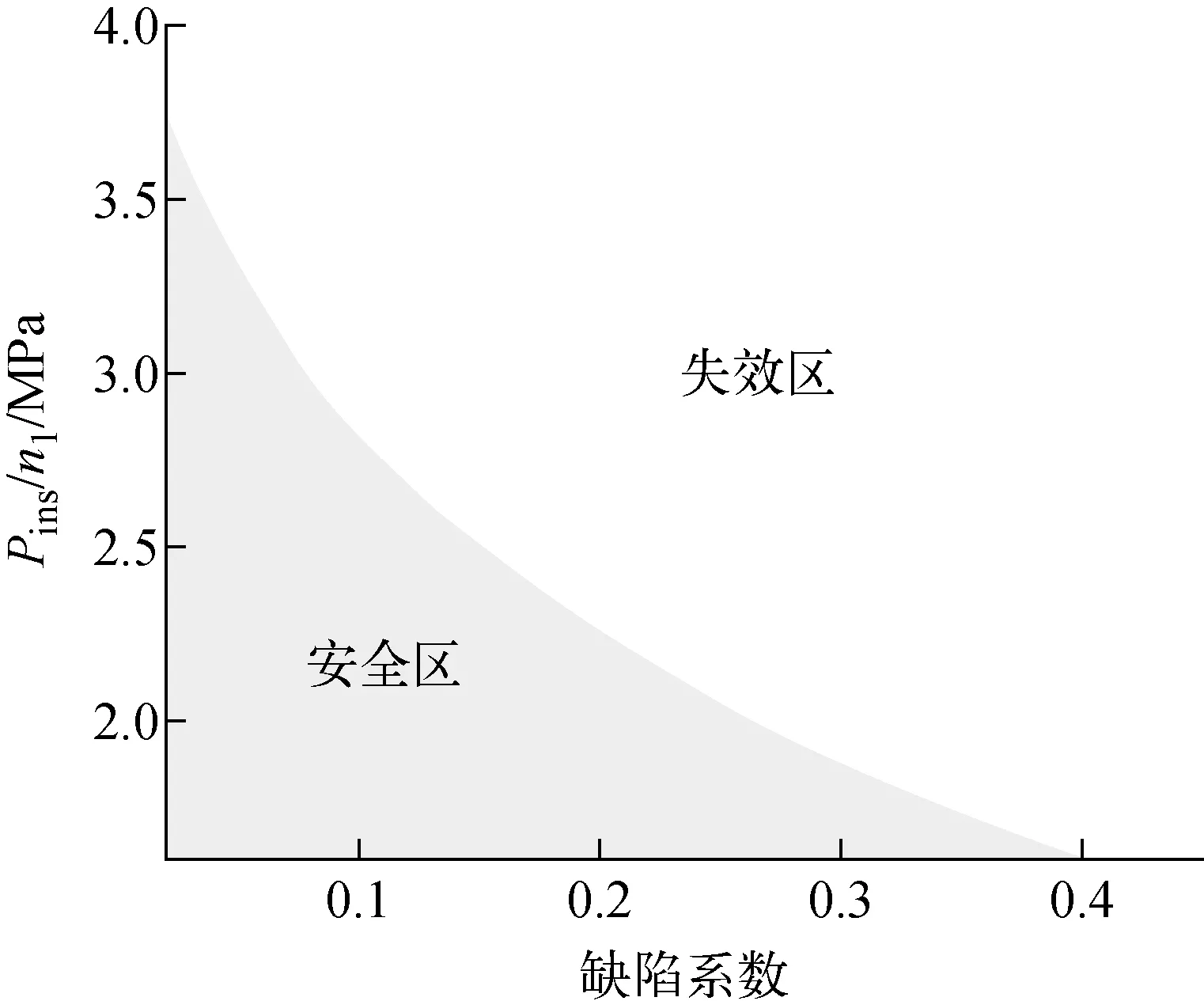
图12 初始缺陷不确定的瞬时屈曲的失效评定图Fig.12 Instantaneous buckling failure assessment diagram with uncertain initial defect
5 压力瞬态下的蠕变屈曲
由于翅片管所受到的外压载荷一般不会一直恒定,会随时间发生变化。在工程中,通常采用恒定的最大压力进行蠕变屈曲分析,但这种处理方式保守性较大,在其不满足评定准则的情况下,为去保守性,应施加实际的压力瞬态,计算临界屈曲时间。
本文计算了3种不同压力瞬态下的临界屈曲时间,如图13所示。图13a、b、c中2 MPa压力的持续时间相同,均为50 000 h,但发生的时间阶段不同,图13a发生在0~50 000 h,图13b发生在10 000~60 000 h,图13c发生在50 000~100 000 h。经计算,3种压力瞬态下的临界屈曲时间分别为145 250、303 722、461 111 h,2 MPa恒压下为67 534 h。可见,不同压力瞬态下的临界屈曲时间不同,但都长于保守地按最大压力计算的临界屈曲时间。
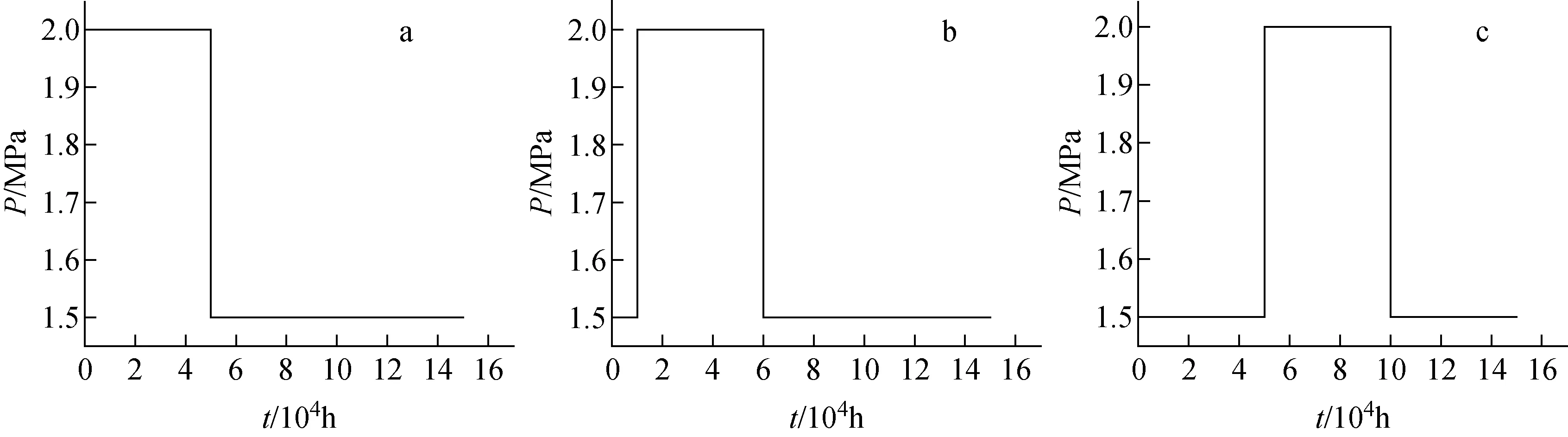
图13 压力瞬态Fig.13 Pressure transient
6 结论
本文根据翅片管的结构特点,将其简化成圆柱壳,采用数值分析的手段得到一套长时蠕变屈曲的分析及评定方法,具体如下:1) 通过与规范解法结果对比,验证了采用有限元解法确定结构蠕变屈曲临界时间的合理性与有效性;2) 得到了部分参数确定情况下的蠕变屈曲失效评定图,并通过数值拟合,获得了保守的评定准则关系式;3) 研究了压力瞬态对蠕变屈曲临界时间的影响。
综上所述,本文提出了一套基于有限元解法的高温翅片管的蠕变屈曲分析及评定方法,解决了不在规范解法适用范围内的蠕变屈曲分析及评定的问题,为复杂结构和复杂载荷工况的蠕变屈曲分析提供了方法上的准备。