核热推进系统氢气物性及流动换热模型分析

韩梓超，章 静,*，王明军，田文喜，苏光辉，秋穗正

(1.西安交通大学 能源与动力工程学院 动力工程多相流国家重点实验室，陕西 西安 710049；2.西安交通大学 核科学与技术学院 陕西省先进核能技术重点实验室，陕西 西安 710049)

核热推进(NTP)是一种空间推进技术，其相关研究工作自20世纪40年代已经开始。核热推进系统利用核反应堆释放的能量直接加热推进工质，高温推进剂进入喷管中膨胀做功进而产生推力。在NASA的载人火星探测技术文件DRA5.0[1]中，核热推进被列为首选的推进方案。核热推进具有比冲高、推力大、寿命长等优点[2]，是人类未来大规模空间活动的必然选择[3]。研究表明，基于现有技术，在不大规模改动发动机尺寸的前提下，仅提高推进剂容量即可将往返火星的单程时间缩短一半[4]，可有效减少宇航员在宇宙中停留的时间，保障其安全。核热推进是未来空间推进最有前景的动力形式，我国对于核热火箭发动机的研制工作需要进一步开展[5]。

氢气是空间核热推进系统典型的推进剂，其流动换热计算是核热推进反应堆热工水力计算的基础。传统的反应堆热工水力计算多使用系统分析程序，如RELAP5、TRACE等。Wang等[6]使用RELAP5程序对CPR1000反应堆在全厂断电事故下非能动余热排出系统进行了分析计算，还对一个固有安全小型轻水堆在小破口事故下安全壳内各非能动系统的热工水力特性进行了分析[7]，系统分析程序具有运算快、结果偏保守等优点，在核反应堆研究领域得到了广泛的应用。典型的适用于核热推进系统的程序有ELM[8]和SAFSIM[9]等，ELM程序主要应用于核热推进反应堆燃料元件稳态热工水力计算，Walton[8]使用该程序对NRX反应堆开展了相关计算，结果显示流体温度、壁面温度、压降等计算结果与实验值符合良好，Walton在报告中还汇总了氢气的流动换热经验关系式，具有较高的参考价值。国内有关核热推进系统分析程序开发的工作较少，为切实保障核热推进反应堆的研究设计工作，相关程序的开发应当尽早开展。

本研究基于现有的适用于压水堆的系统分析程序进行二次开发，添加氢气的物性模型及流动换热和摩擦阻力关系式，使其适用于核热推进系统内氢气的流动换热计算，采用公开文献中的实验数据及计算结果对相关模型进行验证。此外，使用该二次开发的系统程序对一种典型的折流式核热推进反应堆堆芯建模，并开展相应的计算及分析。

1 数值模型

1.1 氢气物性模型

核热推进系统中温度、压力变化范围大，对氢气物性模型的精度要求较高。本研究参考房玉良等[10]关于高温氢介质物性的研究内容，针对核热推进反应堆堆芯，所采用的氢气物性模型适用范围为温度300～3 000 K、压力0.1～15 MPa。比容、比热容、热导率和黏度的物性模型如下。

对于比容的求解采用Aungier-Redlich-Kwong(ARK)真实气体模型[11]：

(1)

式中：a(T)、b、c均为系数，各系数的详细表达式参见文献[11]；p为压力，Pa；R为氢气气体常数，R=4 124.5 J·kg-1·K-1；T为温度，K；V为比容，m3·kg-1。

(2)

式中，ui、vi均为系数，各系数的值参见文献[12]。实际气体比定压热容与理想气体比定压热容之间的关系式可参考文献[10]。

对热导率λ(ρ，T)的求解采用Assael模型[13]：

λ(ρ,T)=λo(T)+Δλ(ρ,T)+Δλc(ρ,T)

(3)

式中：λo(T)为稀薄气体热导率；Δλ(ρ，T)为附加热导率；Δλc(ρ，T)为临界增量；ρ为密度，kg·m-3。

对黏度η(T，ρ)的求解采用Muzny模型[14]：

(4)

式中：η0(T)为零密度极限条件下的黏度；η1(T)为相对于零密度条件由密度大于零引入的黏度增量；c1～c6为系数；Tr为对比温度；ρr为对比密度。

1.2 氢气流动换热关系式

房玉良等[15]采用ANSYS FLUENT对高温、高流速氢气在圆管内的流动换热特性做了研究，对比了程序计算值与经验关系式求得的换热系数，结果表明，修正的Miller-Taylor关系式符合较好，其表达式如下：

(5)

式中：Nu为努塞尔数；Re为雷诺数；Pr为普朗特数；L为通道长度；D为水力直径；下标W、b表示壁面和主流。该关系式的适用范围为：Re，3×104～4×105；TW/Tb，1.1～8。

1.3 氢气摩擦阻力关系式

Walton在文献[8]中整理了ELM程序采用的流动换热关系式及摩擦阻力关系式，具有较高的参考价值。本研究模拟了氢气在某燃料元件内的流动，对比了采用文献[8]中不同摩擦阻力关系式进行计算的结果，具体内容见2.2节，在保证燃料元件压降计算结果与参考值符合较好的前提下，推荐使用形式简洁的Koo关系式：

(6)

式中，f为摩擦系数。

2 数值模型验证

选用Taylor[16]的实验数据验证氢气的物性模型，选用ELM程序对NRX反应堆燃料元件的模拟结果验证流动换热关系式和摩擦阻力关系式。

2.1 氢气物性模型验证

20世纪五六十年代，为研究核动力火箭发动机，美国开展ROVER项目，设计、建造并测试了多种氢气冷却反应堆及核动力火箭系统，期间开展了大量有关氢气流动换热的实验。Taylor[16]发表了关于氢气和氦气在圆管内流动换热实验的研究成果，该实验采用的试验段由金属钨制成，试验段长为0.227 m，内径为2.946 mm，管壁厚为1.587 mm。该实验测量了流量、进出口流体温度和压力以及管道外壁面温度等参数，并整理得到摩擦系数和对流换热系数的经验关系式。

该报告中共有18组关于氢气流动换热的实验数据，为充分验证氢气物性模型的正确性，本研究分别使用系统程序和ANSYS FLUENT对试验段建模并计算，管道入口采用流量边界，出口采用压力边界，给定入口流体的温度和加热功率。系统程序建模节点图如图1所示，入口处时间相关控制体给定入口流体温度，时间相关接管给定入口流量，出口处时间相关控制体给定出口压力，加热功率由热构件输入。

图1 圆管内氢气流动换热计算系统程序建模节点图Fig.1 Nodalization of system code modeling of hydrogen flow and heat transfer calculation in circular tube

需要注意的是，文献[16]中给出的温度是总温，而程序计算得到的温度是静温，总温与静温之间的关系为：

(7)

式中：Ttotal为总温，K；Ts为静温，K；γ为比热容比；Ma为马赫数。

氢气圆管内流动换热计算结果与实验值的对比如图2所示，系统程序与CFD程序计算结果的相对误差均在10%以内，而CFD程序的计算结果与实验值符合更好。结果表明，采用1.1节所述的氢气物性模型能较好地模拟氢气在圆管内流动换热的问题，出口总温计算相对误差小于10%，能满足系统程序的计算要求，而对于简单的氢气流动换热问题，CFD程序的模拟精度更高。

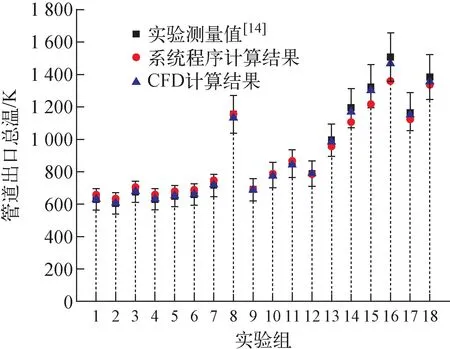
图2 氢气圆管内流动换热计算结果与实验值的对比Fig.2 Comparison of calculated result and experimental data of hydrogen flow in circular tube

2.2 流动换热及摩擦阻力关系式验证

Walton[8]使用ELM程序对NRX反应堆的六边形燃料元件进行了计算，本研究选用NRX-A3反应堆燃料元件的实验参数(表1)，燃料元件的几何及简化模型示意图如图3所示。

图3 燃料元件几何及简化模型示意图Fig.3 Scheme of geometry and simplified model of fuel element

表1 NRX-A3反应堆燃料元件实验参数[8]Table 1 Experiment parameter of fuel element of NRX-A3 reactor[8]

使用系统程序对该燃料元件建模并计算，燃料元件简化为单通道模型，模型、边界条件与2.1节氢气物性模型验证部分相一致，节点图如图1所示，功率分布参考文献[8]。采用不同摩擦阻力关系式进行计算，燃料元件通道内压力的计算结果如图4所示。取ELM程序计算结果的1%为相对误差，结果显示，采用Koo关系式、Taylor Ⅱ关系式和GRAPH-I-TITE G关系式计算得到的压力结果均在误差范围内，而采用Taylor Ⅰ关系式和基本摩擦系数关系式计算得到的压力在靠近燃料元件出口处超出了误差范围。综合考虑结果的准确性和公式的简洁性，推荐使用Koo关系式。

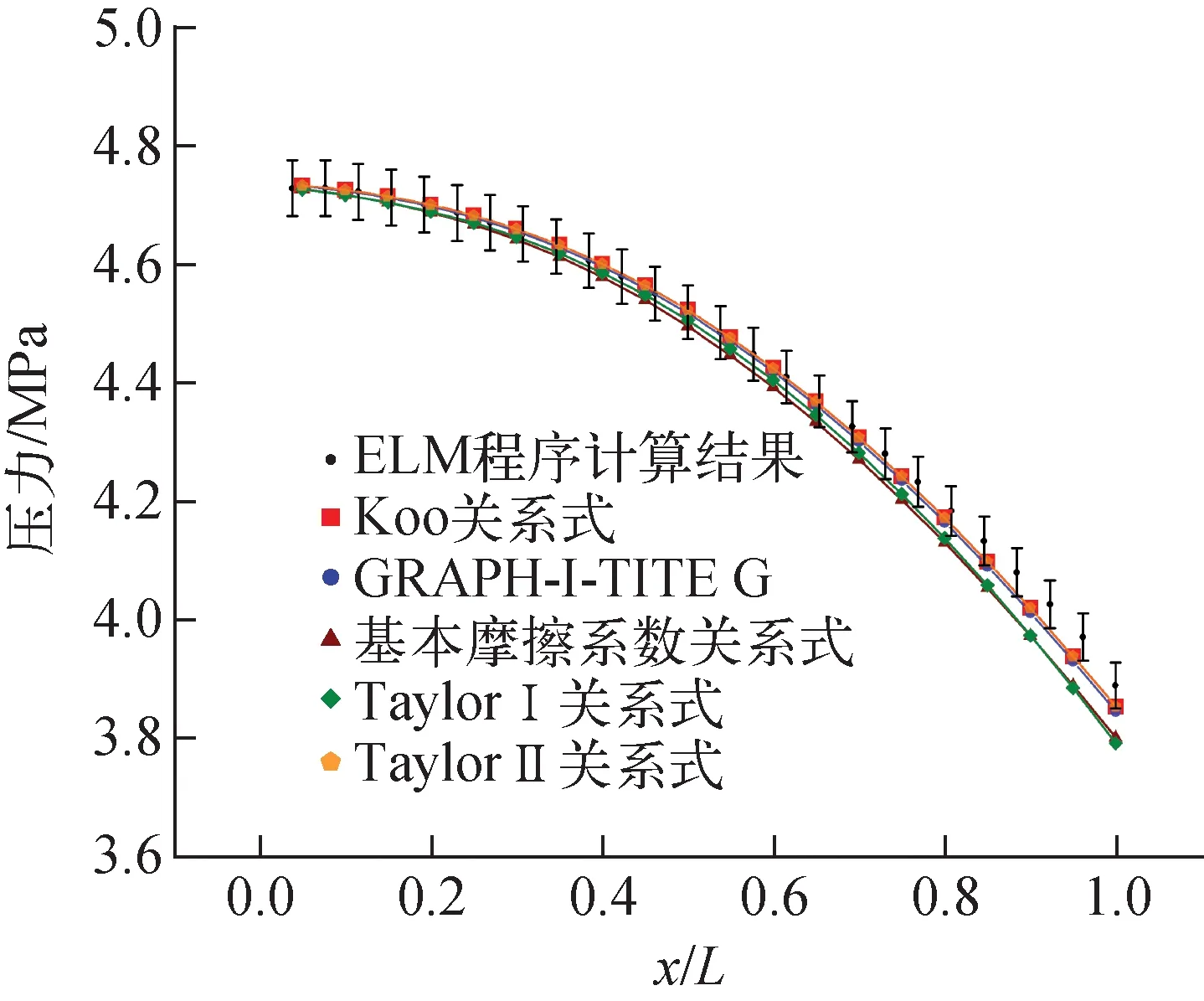
图4 燃料元件压力计算结果对比Fig.4 Comparison of pressure calculated result of fuel element

摩擦阻力关系式采用Koo关系式，流动换热关系式采用修正的Miller-Taylor关系式，流体温度及壁面温度的计算结果与文献值的对比如图5所示。由图5可看出，二次开发系统程序的计算结果与ELM程序的计算结果符合较好。除压降、流体温度和壁面温度外，燃料元件内雷诺数与马赫数的计算结果均符合良好，流动换热及摩擦阻力关系式的选择是合理的。

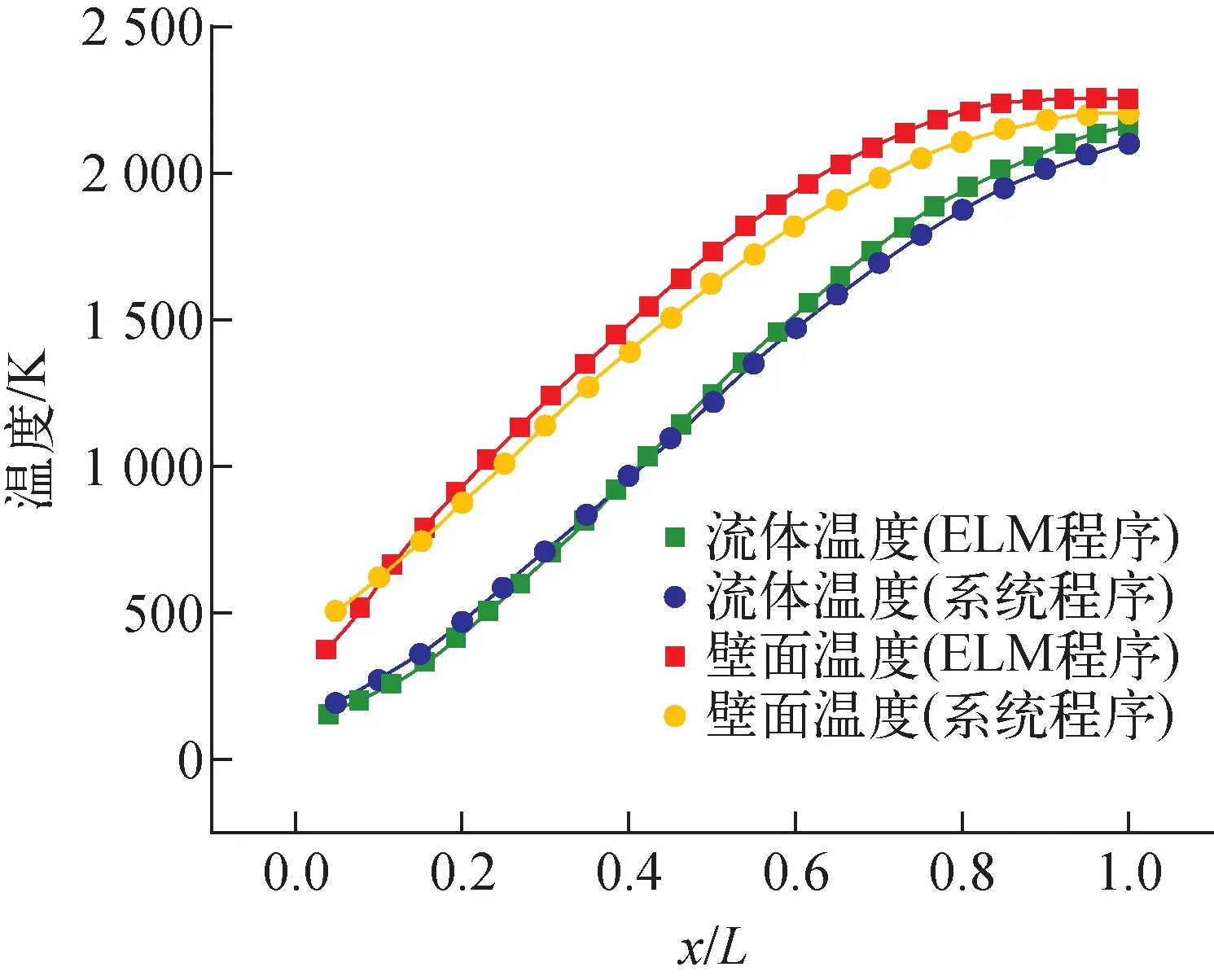
图5 燃料元件温度计算结果对比Fig.5 Comparison of temperature calculated result of fuel element

3 折流式核热推进反应堆堆芯计算

3.1 折流式核热推进系统简介

折流即冷却剂主流在堆芯不同区域内存在方向相反的流动，典型的折流式核热推进系统如图6所示，主要包括液氢储箱、涡轮泵、再生冷却通道、径向反射层、外侧环形堆芯、轴向反射层、内侧柱形堆芯和喷管等部分，为方便表述，外侧环形堆芯简称为外堆芯，内侧柱形堆芯简称为内堆芯。低温液氢在泵的作用下进入系统，随后在喷管喉部再生冷却通道中吸收热量实现预热，在此过程中，氢工质会跨越拟临界点，物性变化比较剧烈[17]。超临界氢气随后进入径向反射层，吸收反射层释放的热量，之后推动涡轮，涡轮带动泵转动提供压头，此过程会伴随较大的压降。从涡轮流出的氢气进入外堆芯，吸收外堆芯区域燃料元件释放的热量后，流经与外堆芯相邻的轴向反射层，进入上腔室。在上腔室中，氢气的流动方向发生改变，同时与来自不同燃料元件的氢气充分交混，可有效降低氢气温度的不均匀程度[18]。交混后的氢气流经与内堆芯相邻的轴向反射层后，进入内堆芯进一步加热至出口温度达2 500 K以上。最后高温氢气在缩放喷管中膨胀做功，将内能转化成动能，为飞行器提供推力。

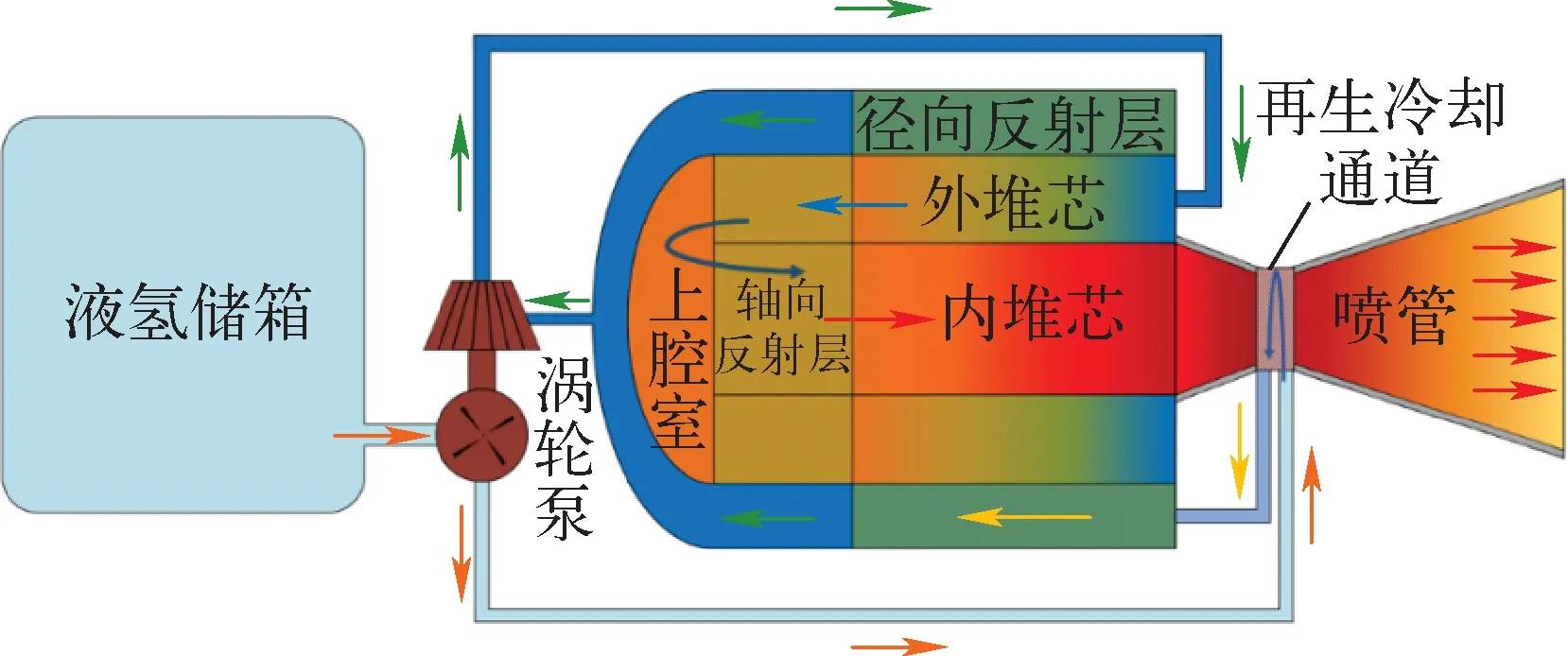
图6 折流式核热推进系统示意图Fig.6 Scheme of two-pass NTP system

3.2 反应堆堆芯几何及建模

本研究针对的核热推进反应堆采用CERMET燃料，将UO2或UN燃料颗粒弥散在钨金属基体中，最高运行温度可达2 900～3 270 K，具有更安全、更经济的优势[19]。若全堆采用金属钨作基体材料，由于密度较高，会导致堆芯质量过重，降低推重比。采用折流式反应堆设计，其堆芯结构如图7所示，将核热推进反应堆划分为外堆芯和内堆芯两个区域，温度较低的外堆芯区域选用金属钼作基体材料，这样可有效降低堆芯总质量。基体材料金属钨及金属钼的热导率列于表2，密度及比定压热容列于表3。

表2 基体材料的热导率[20]Table 2 Thermal conductivity of substrate material[20]

表3 基体材料的其他热物理性质[20]Table 3 Other thermophysical property of substrate material[20]

图7 折流式核热推进反应堆堆芯示意图Fig.7 Scheme of two-pass NTP reactor core

本文主要内容为氢气相关模型的验证及应用，运行参数、尺寸数据等仅根据经验选取，初步设计堆芯高度为80 cm，总功率为495 MW，单个燃料元件的流通面积约为2.6×10-4m2。使用系统程序对该反应堆堆芯建模，为节省计算资源，取堆芯的1/6作为研究对象。程序采用单通道模型，将每个六边形圈上的燃料元件等效为1根管，水力直径取燃料元件上单个孔道的直径，流通面积取所有孔道的流通面积之和，堆芯截面图如图8所示，其中不同颜色代表不同的单通道。

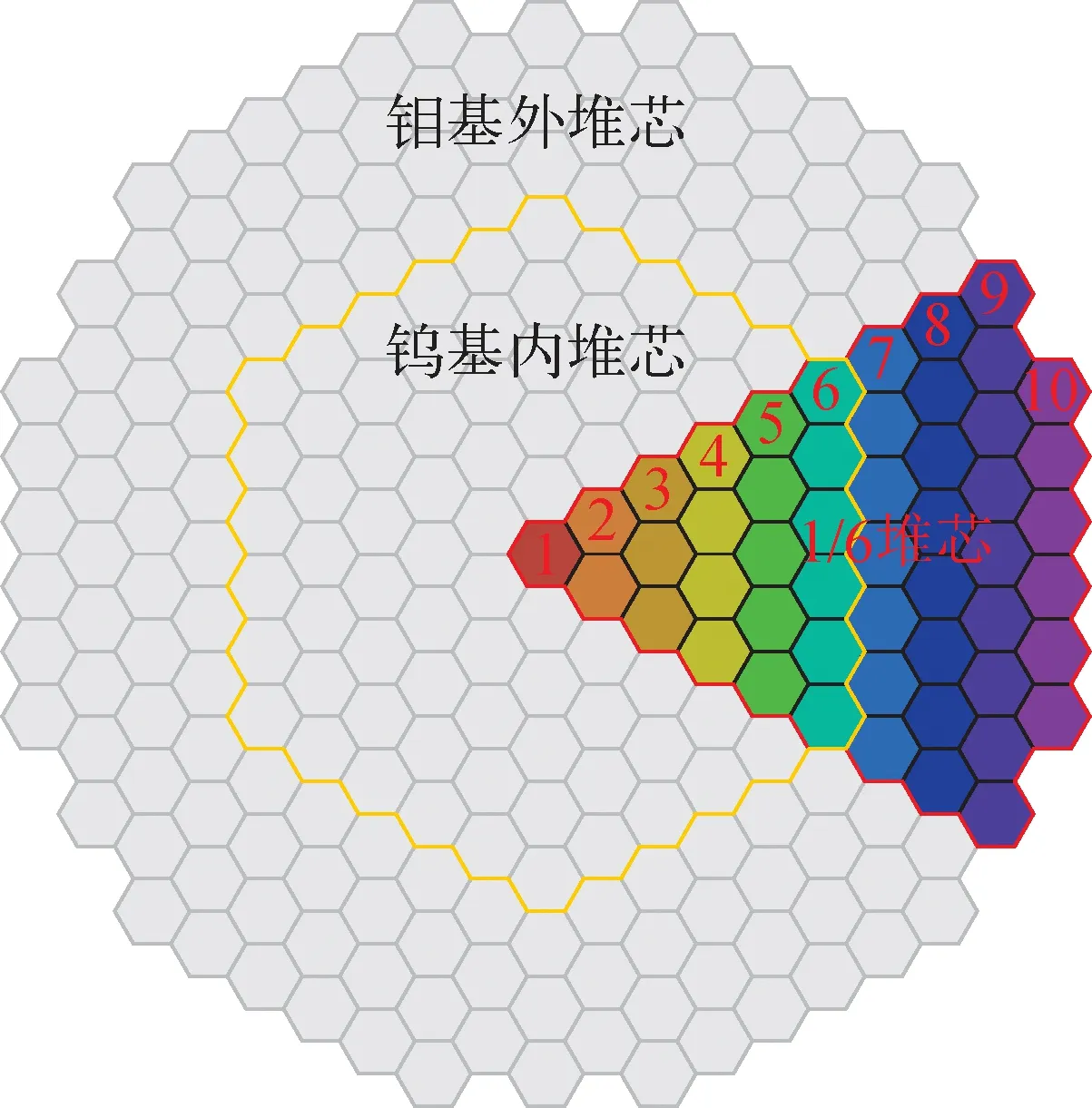
图8 反应堆堆芯径向截面示意图Fig.8 Radial cross section scheme of nuclear reactor core

系统的入口采用流量边界条件，同时给定入口流体的温度；出口采用压力边界条件；堆芯燃料元件与轴向反射层相连，共等效为10根管型部件；上腔室等效为单一控制体；不同管型部件之间使用热构件相连，模拟堆芯径向不同位置的燃料元件之间的热传导，堆芯的释热功率通过热构件输入。系统建模的节点图如图9所示。

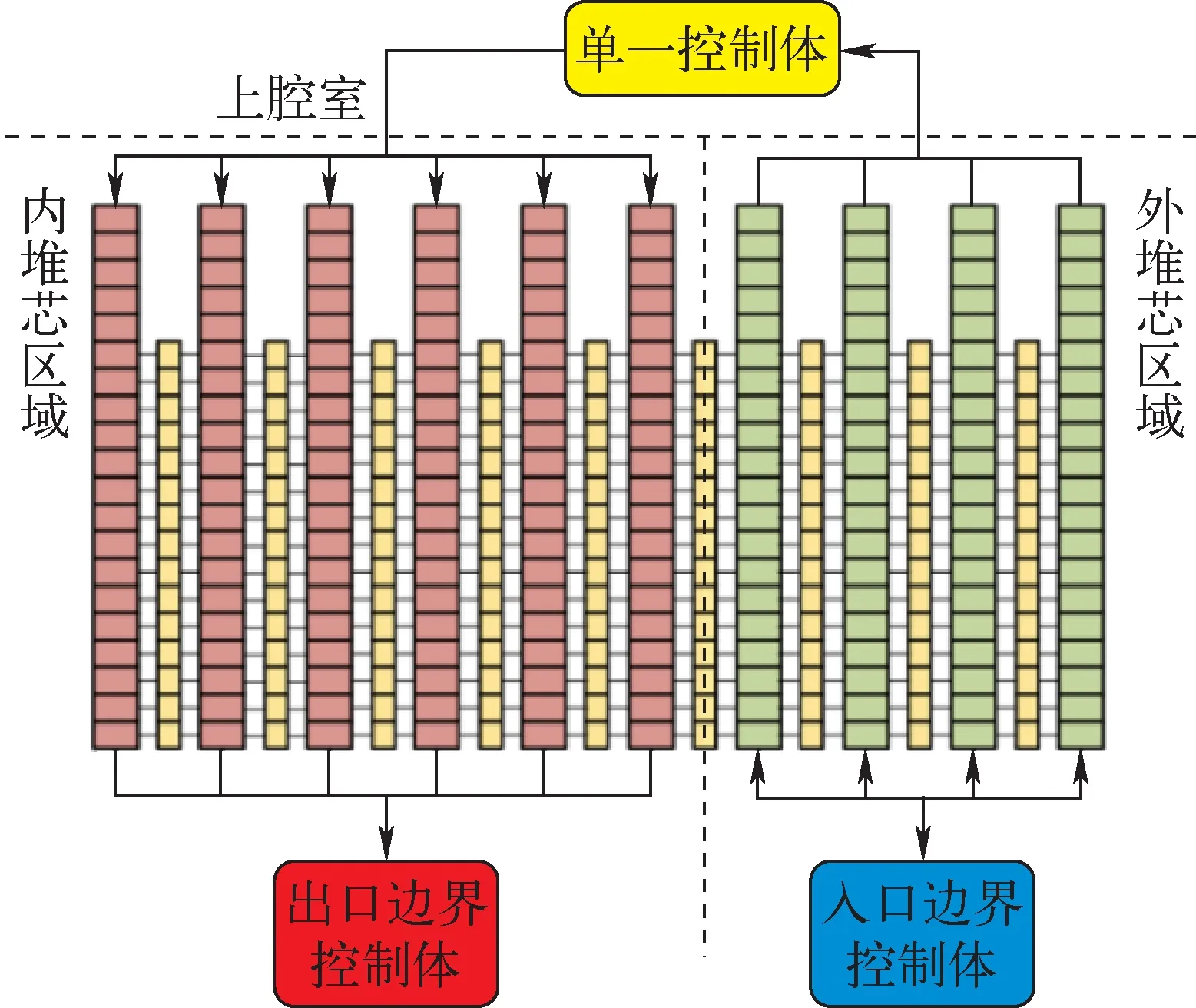
图9 1/6堆芯建模节点图Fig.9 Modeling nodalization of 1/6 reactor core

3.3 稳态热工水力计算

在前期的核热推进反应堆堆芯设计工作中，通过合理设计不同燃料元件的富集度，可以展平径向功率，不同通道的归一化功率分布如图10中柱状图所示，对于内堆芯区域的通道1～6，功率分布较为均匀，且沿径向由内向外功率逐渐减小，对于外堆芯区域的通道7～10，通道7、8和9功率相近，通道10由于距离径向反射层比较近，中子通量水平相对较高，功率较高。输入某组设计工况的边界条件进行计算，可得到相应的稳态热工水力结果，1/6堆芯的归一化流量分布如图10中散点图所示。可以看出，由于内堆芯功率分布较为均匀，且氢气在上腔室中混合后再流入内堆芯，内堆芯区域不同通道间的流量分布较为均匀。而外堆芯的流量分布不均匀程度较高，通道8和9由于功率水平较低，其流量高于外堆芯通道的平均值；特殊的是，对于与内堆芯区域相邻的通道7，虽然其燃料元件功率低于外堆芯平均值，但其流量也低于平均值，且相差超过15%。

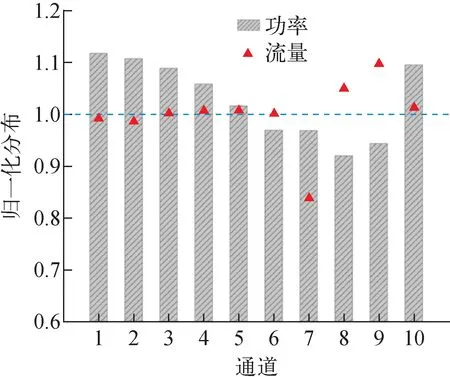
图10 1/6堆芯归一化功率及流量分布Fig.10 Normalized distribution of power and mass flow rate of 1/6 reactor core

该核热推进反应堆采用的CERMET燃料为多孔棱柱形燃料，堆芯内的流动属于典型的并联通道间流动，并联通道间的释热不均易引发流量分配的不均匀。由外堆芯区域功率及流量分布情况可看出，对于折流式核热推进反应堆，功率无法真实反映释热的水平，需对比不同通道内流体的焓升来衡量堆芯释热的均匀程度。1/6堆芯归一化焓升如图11所示。通道6的焓升低于内堆芯的平均水平，而通道7的焓升高于外堆芯的平均水平，这是由于内外堆芯温度差别较大，在交界处存在较强的热传导，部分内堆芯燃料元件释放的热量传递到外堆芯，因此在外堆芯区域，通道7的功率虽然较低，但其释热量远高于平均值，在此影响下其流量远低于平均值。

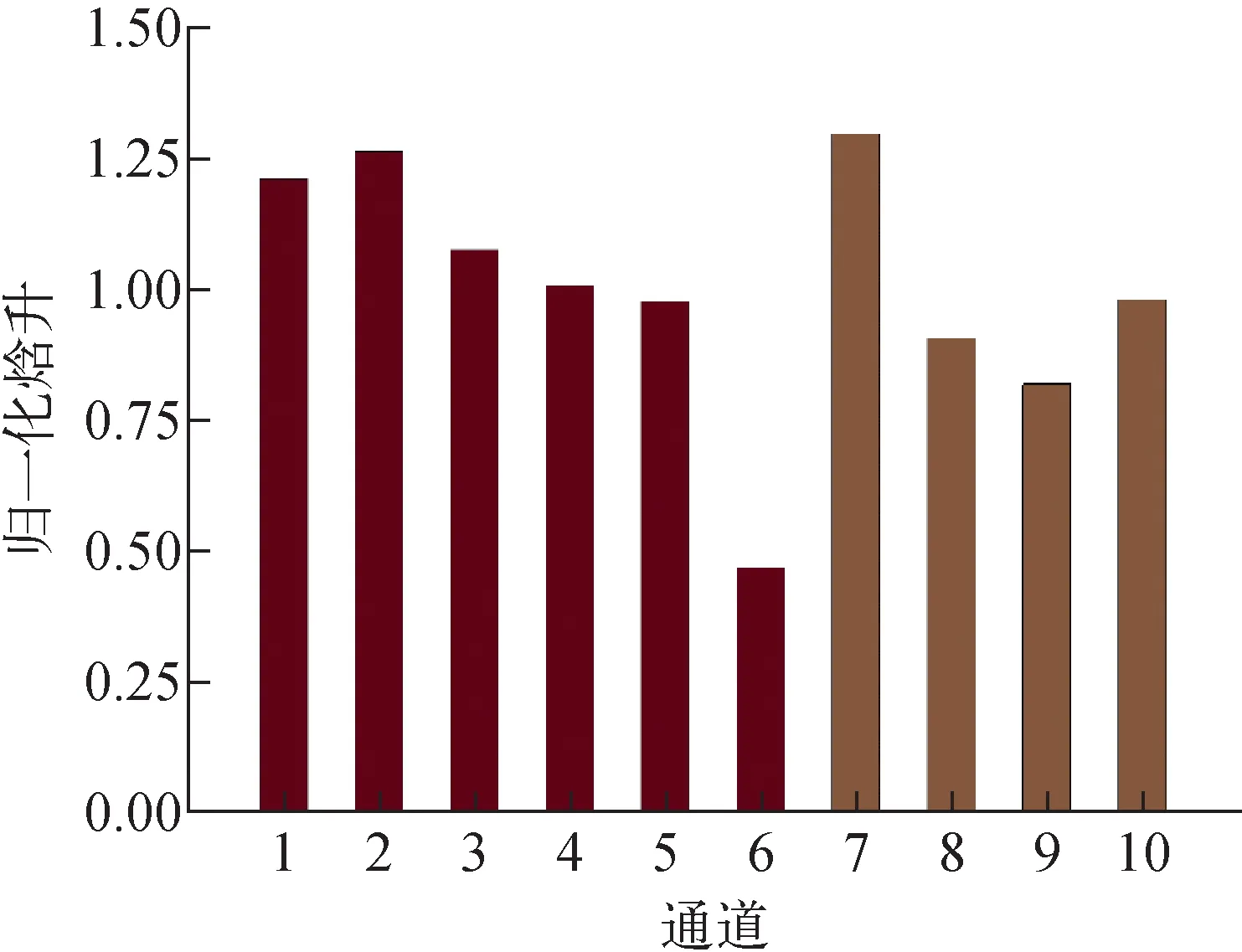
图11 1/6堆芯归一化焓升分布Fig.11 Normalized distribution of enthalpy rise of 1/6 reactor core

内外堆芯之间的热传导增加了堆芯释热的不均匀程度，造成个别燃料元件内的参数与平均值相差较大，危害系统的稳定性。另外，对于外堆芯区域最内侧的燃料元件(通道7)，其流量较低，释热量较高，易造成基体材料温度超过限值，危害反应堆的安全。综上所述，在折流式核热推进反应堆堆芯的反应堆物理设计中，尤其对于外堆芯区域具有不同富集度的燃料元件的布置，由于内外堆芯之间存在较强的热传导，不能盲目地追求功率展平，应当结合堆芯的稳态热工水力计算，合理设计堆芯方案，使得冷却剂流体温度、流量等参数沿径向分布尽量均匀，提高反应堆的安全性。

4 结论

本研究将氢气的物性模型、流动换热及摩擦阻力关系式植入一系统分析程序中，分别采用实验数据及程序计算结果进行了验证，使用该程序对折流式核热推进反应堆堆芯建模并计算，所得结论如下。

1) 采用本文所述氢气物性模型，对某圆管内氢气流动换热实验的计算相对误差小于10%；采用推荐的流动换热及摩擦阻力经验关系式，对某燃料元件内氢气流动换热的模拟结果与参考值符合较好。

2) 本研究采用的系统分析程序经二次开发，能应用于核热推进系统的建模与计算，而程序的适用性、计算结果的准确性需要更多的验证及分析。

3) 对于折流式核热推进反应堆，内外堆芯之间的热传导增加了堆芯释热的不均匀程度，对堆芯稳态特性影响较大，堆芯方案的设计应结合相应的热工水力计算，确保温度、流量等重要参数沿径向分布均匀，提高安全性。