基于集成MZI滤波器的宽带微波频率与到达角测量方法

齐 跃,董 代

（1.92941部队,葫芦岛 125001;2.北京航天控制仪器研究所,北京 100039)

0 引言

微波频率和微波到达角测量技术是电子战侦察系统中的关键技术。随着微波技术的不断发展,各种微波武器和新的作战形式不断涌现,更高频率、更大带宽的微波信号的使用不断增多,微波测量技术也需要适应高频宽带信号的测量。然而,传统的基于电子器件的微波测量系统受限于瞬时带宽小、高频损耗大等固有瓶颈的限制,对高频微波信号的测量需要引入更复杂的测量设备,使得系统庞大、抗电磁干扰能力差。微波光子学的发展为解决上述问题开辟了新的道路。由于光波的频率远高于微波,基于光子的微波信号测量系统天然地具有超大的带宽,而光学系统又同时具备损耗小、质量小、抗电磁干扰能力强的优势,使其在未来雷达、通信、电子战系统中发挥重要作用［1］。

微波光子学对宽带微波频率的测量方法解决了频率-功率映射、频率-空间映射、频率-时间映射和光子压缩感知等几类关键技术［2-5］。基于上述技术的微波光子频率测量方法已经能够实现对接近40GHz带宽的微波信号进行频率测量,频率测量精度达到100MHz［6］。

微波到达角测量方面,其测量方法是:将两个具有相位差的微波信号调制到光载波上,并通过调制本振信号或调制器偏置点实现微波相位差到输出光信号功率的映射,从而实现相位差的测量,进而计算微波信号到达角［7-9］。例如,Cao等［9］提出了基于双驱动调制器的微波相位差测量方案,将待测微波调制到双驱动调制器两臂上,通过控制直流偏置消除光载波,调制器输出的光信号是两臂中光边带的干涉叠加,其光功率是两微波相位差的函数,从而可以通过光功率来测量微波相位差。近年来,研究者们基于双平行调制器、双偏振调制器等离散器件实现了宽带微波信号到达角的高精度测量［10-11］。Lin等［11］提出了基于双平行二进制相移键控的二维到达角测量,通过测量排列成L形的三个天线接收到信号的相位差,实现了三维的目标测向。然而,基于光纤分立器件的微波光子测量系统有着可靠性差的缺点,光纤本身和光纤间的连接都容易受到环境温度、振动等因素的影响,使得光纤中传输的光载微波信号的相位、偏振态发生随机的抖动涨落,从而导致系统的不稳定,极大地削弱了系统的性能。将调制器、探测器以及光子处理器件（滤波器、延时器等）集成到单个光子芯片上可以避免振动对不同器件的影响,并可以通过温控装置对芯片上所有光子器件进行统一的调控,极大地提高了系统可靠性。目前,基于集成光子技术的微波光子测量方案已有诸多报道［12-15］,例如,Zhang等［16］基于单个芯片上的微环辅助马赫-曾德尔干涉（Mach-Zehnder Interferometer,MZI）滤波器,实现了5GHz～39GHz的微波频率测量范围和37MHz的测量精度。然而,在上述的微波到达角测量方案中多是对已知频率微波的测量,在实际应用场景中往往需要对未知频率信号的到达角进行测量,这就需要测量系统能同时对微波频率和相位差进行测量。因而,将测频、测相等多种功能一体化集成将是微波光子测量系统的发展趋势。

本文提出了一种基于载波抑制双边带调制和MZI结构的集成光子辅助微波频率和到达角测量方案,通过单个测量链路同时实现微波频率和微波到达角的测量。两路微波信号来自同一个辐射源,在接收端通过两个天线进行接收（两微波信号的频率相同,但存在一定的相位差）,两微波信号通过载波抑制双边带调制,得到两路光载微波信号。两路光载微波信号通过MZI滤波器滤波,并通过控制MZI滤波器上的移相器调谐MZI滤波器的滤波频率,使其变化超过一个自由光谱范围（Free Spectral Range,FSR）,此时光边带的功率也会随之发生变化。这时通过测量光功率变化的振幅,就可以得到微波信号的频率。两路光载微波信号通过MZI干涉仪将相位差映射成光功率,通过光电探测器可以对两路信号的相位差进行测量,根据频率和相位差可以计算得到微波信号的到达角。此方案的测频方法对系统初始相位、激光器频率稳定性要求较低,对光学处理器件频率稳定性的要求也不高,避免了复杂的调制和光学处理器件频率控制环节,具有广阔的工程应用前景。

1 基于集成MZI滤波器的微波光子频率测量原理

集成微波光子频率和到达角测量链路由激光器、推挽式调制器、可调谐MZI滤波器、光电探测器和信号处理器构成,如图1所示。其中,马赫-曾德尔调制器、可调谐MZI滤波器、光电探测器可以集成在单个集成光子芯片上以减小器件的尺寸和质量,提高系统可靠性。该链路由三条子链路构成,分别为两条微波频率测量链路和一条微波信号相位差测量链路。图2为微波频率测量链路的示意图。

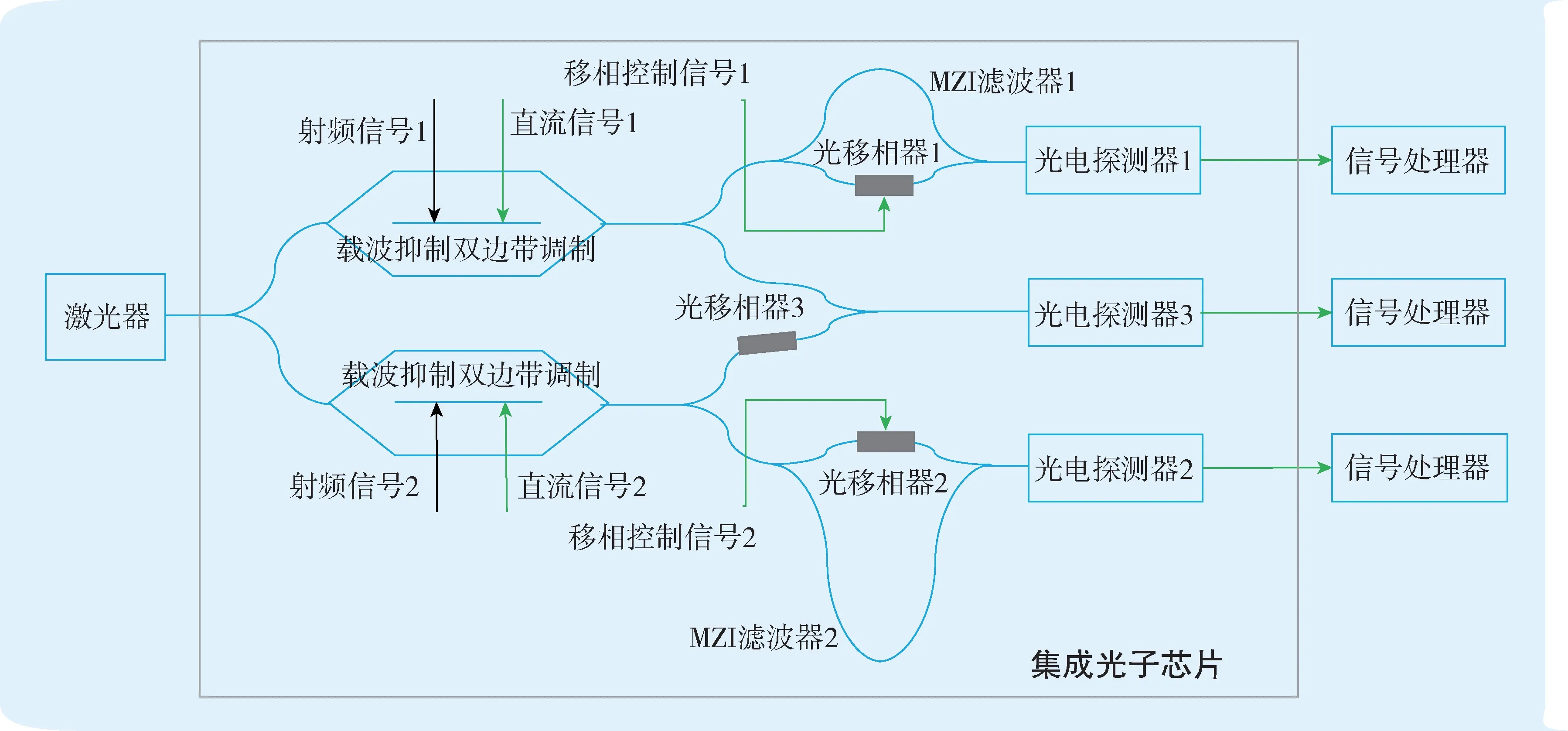
图1 集成微波光子频率测量与到达角测量方案示意图Fig.1 Schematic diagram of integrated microwave photonic frequency measurement and angle-of-arrival measuring scheme

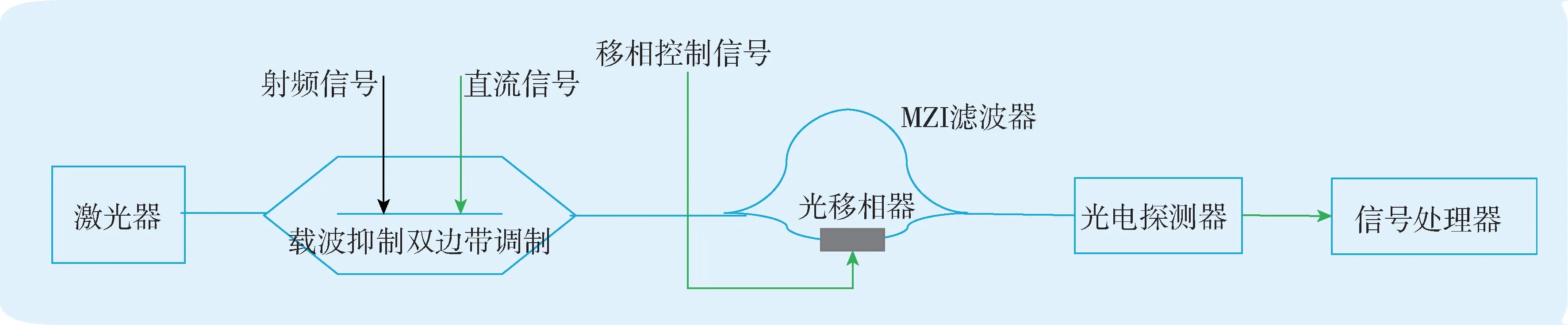
图2 集成光子微波频率测量链路示意图Fig.2 Schematic diagram of integrated microwave photonic frequency measurement link

激光器产生的光载波信号电场可以表示为

式（1）中,Ec为光载波电场强度幅值,ωc为光载波角频率。光载波经推挽式调制器被微波信号调制,通过调控直流偏置使调制器偏置在最小偏置点,从而抑制光载波和偶数阶光边带,实现载波抑制的双边带调制。在小信号调制情况下,高阶光边带的功率很小,因此可以认为此时链路中只存在±1阶光边带,其表达式为

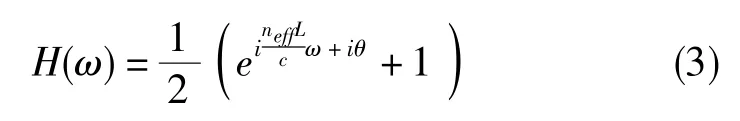
式（3）中,neff为集成光波导有效折射率,L为MZI滤波器两臂的长度差,c为真空光速,θ为移相器引入的相移。那么,滤波后的±1阶边带电场强度为

滤波后的光信号经过光电探测器对两光边带的强度进行测量,对应的直流光电流强度（正比于光边带功率）为

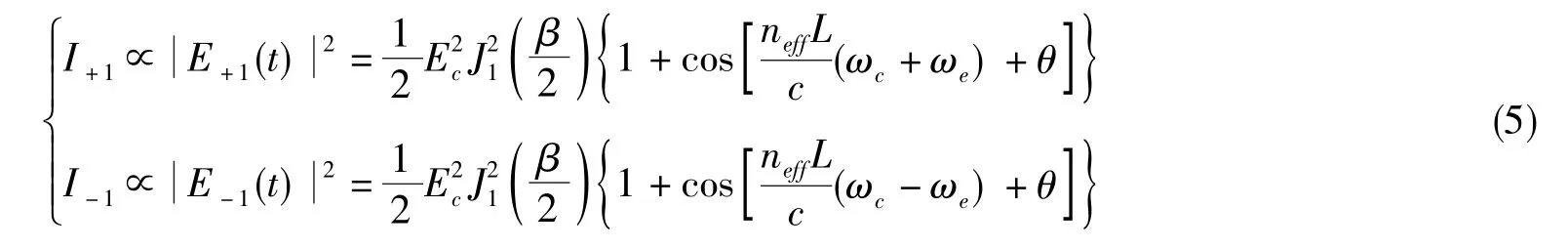
总直流光电流为

如式（6）所示,总直流光电流是移相器相移量θ的余弦函数,且该余弦函数的振幅（即最大值与最小值之差的一半）是微波信号频率的余弦函数。如图3（a）所示,当微波频率接近于0时,不同移相量θ1、θ2的光功率随频率变化曲线如图3（a）的左侧;随着相移量的变化,光电流最小值接近于0,光电流曲线的归一化振幅趋近于1,如图3（a）的右侧。当微波率接近FSR/4时,两光边带的频率差为FSR/2,当相移量变化时,两光边带的功率此消彼长,而总功率保持几乎不变,归一化振幅趋近于0,如图3（b）所示。

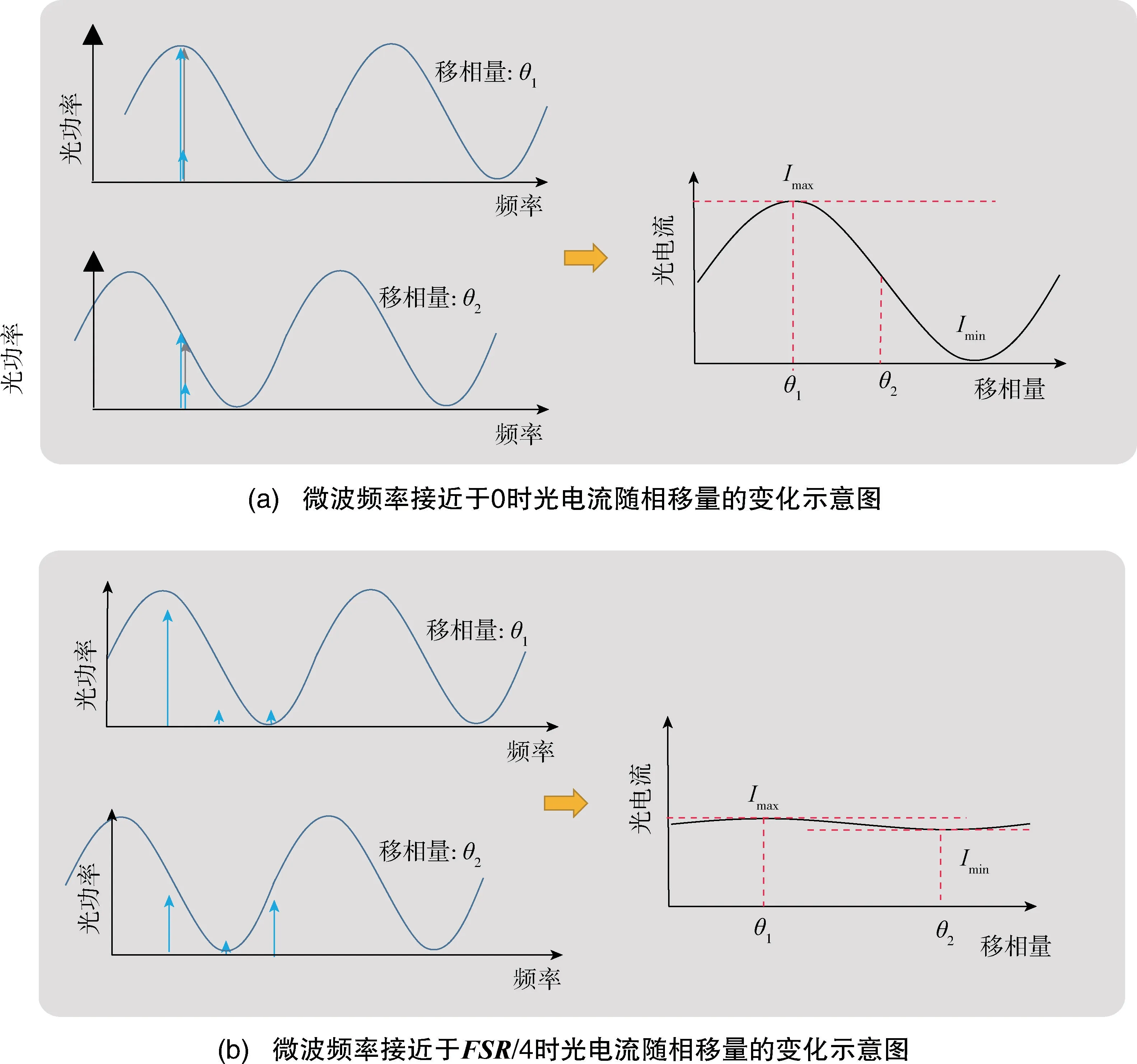
图3 不同微波频率光电流随相移量的变化示意图Fig.3 Schematic diagram of photocurrent variation with phase shift at different microwave frequencies

通过改变θ可以测得直流光电流的最大值Imax和最小值Imin,从而计算出曲线的归一化振幅A和微波信号频率ωe

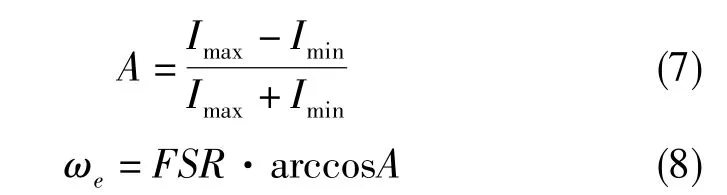
式（8）中,FSR为MZI滤波器的自由光谱范围。通过设计臂长差L,可以实现对MZI滤波器自由光谱范围的设计。根据式（8）,为了保证测量出的微波频率的唯一性,此方案的测量范围（即测量系统的工作频率范围）为0～FSR/4。若设计MZI滤波器的FSR=80GHz,则该测试链路的频率测量范围为0GHz～20GHz。

2 基于集成MZI滤波器的微波光子相位差与到达角测量原理

干涉仪测向是最常用的高精度辐射源到达角测量技术,其原理示意图如图4所示。

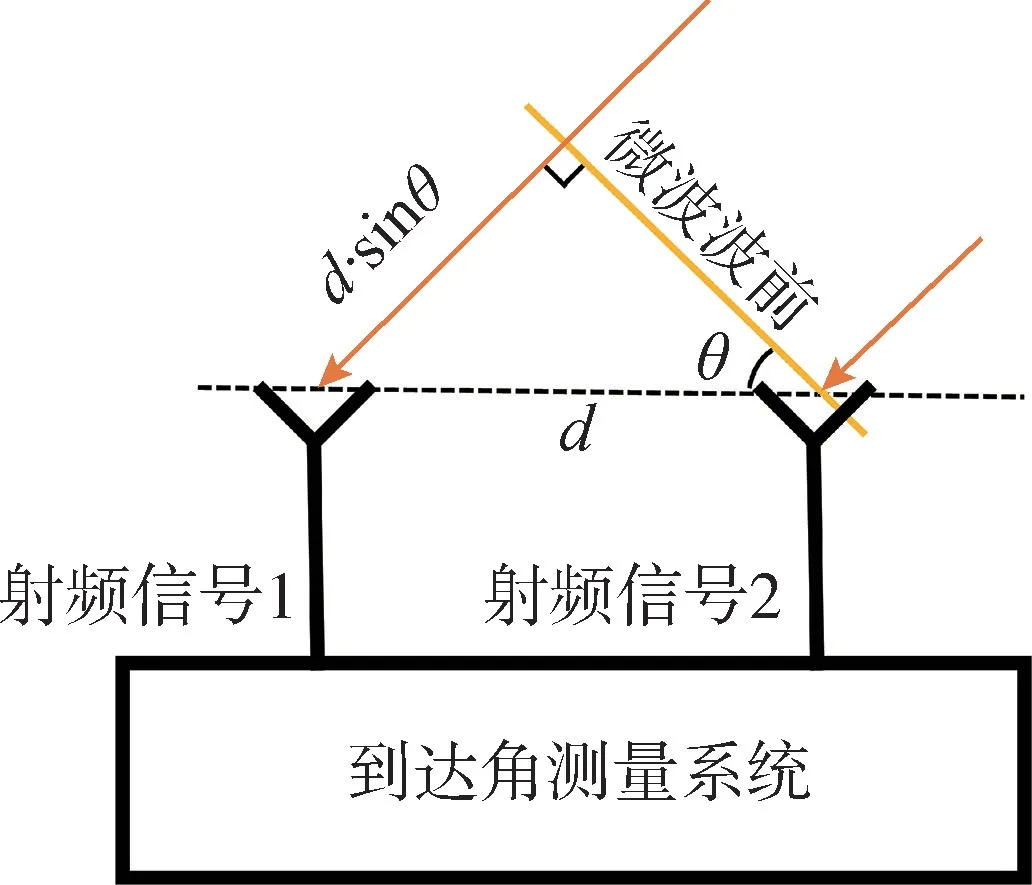
图4 基于干涉仪的到达角测量原理示意图Fig.4 Schematic diagram of angle-of-arrival measurement based on interferometer

若通过两个间距为d的天线对来波方向为θ0的微波进行测向,两天线接收到的微波信号相位差为

通过测量相位差φ,可以计算得到微波信号的到达角度θ0

通过如图5所示的微波信号相位差测量链路,可以对两路微波信号（射频信号1、射频信号2）的相位差进行测量,移相器用于校正两路光信号相位,使它们在初始状态下的相位差为0。

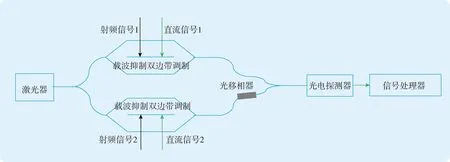
图5 微波信号相位差测量链路示意图Fig.5 Schematic diagram of microwave signal phase difference measurement link

光载波通过光学分束器均分成强度相等的两路信号,并通过载波抑制的双边带调制将射频信号1和射频信号2分别调制到两路光载波上,调制后的信号表达式为

调制后的光载微波信号通过光学合束器,两路上下边带相干,得到合束后的信号表达式为

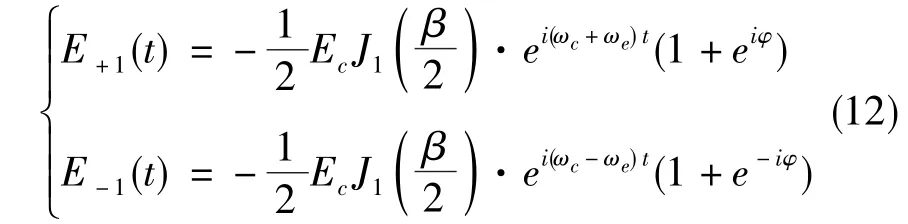
经光电探测器后,输出的直流光电流为上下边带光电流之和

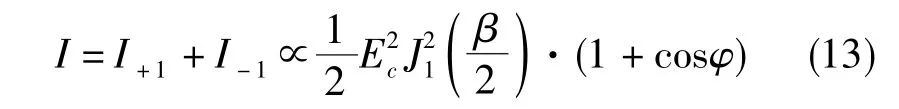
根据式（13）,可以通过测量光电探测器输出的直流光电流来测量两路微波信号的相位差,并基于式（10）计算得到微波信号的到达角。

3 基于集成MZI滤波器的微波光子相位差与到达角的建模仿真实验

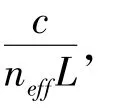
基于式（6）,仿真得到不同微波频率下光电探测器测量得到的光边带的归一化总功率随移相器相移量的变化曲线,如图6（a）所示。基于式（7）和式（8）,光功率曲线的振幅随着微波频率的增大而减小,其变化趋势如图6（b）所示。

在实际测量时,通过对移相器施加驱动信号,控制其相移量,以改变光信号的功率。值得注意的是,相移量与驱动信号之间通常不是线性关系,即光功率曲线通常不是驱动信号强度的余弦函数。然而,只要控制驱动信号使相移量超过2π,就可以测得光功率曲线的最大值与最小值,再根据式（7）和式（8）计算出微波信号频率。此方案由于光信号功率是由移相器相对相移量决定的,不要求激光器波长和滤波器的滤波频率对齐,从而大大降低了链路控制的难度。

基于上述分析,通过测量光功率曲线振幅,可以得到微波信号的频率。然而,当微波频率较低时（图6（b）中频率靠近0GHz时）,光功率曲线振幅随频率的变化幅度较小,可能存在无法分辨两个不同的微波频率;当微波频率较高时（图6（b）中频率靠近20GHz时）,光功率曲线振幅接近0,可能受限于后续信号处理模块的采样精度使得测量不准确。因此,单个链路对工作频率范围内的低频和高频微波的频率测量精度不高。为解决上述问题,对图1中的两路频率测量链路设计具有不同FSR的可调MZI滤波器。若图1中的MZI滤波器1和MZI滤波器2的FSR分别为80GHz和8GHz（两个MZI滤波器的臂长差分别为911.1μm和9.111mm）,那么通过两路光电探测器测得的归一化光功率曲线振幅随调制微波频率的变化如图7所示。

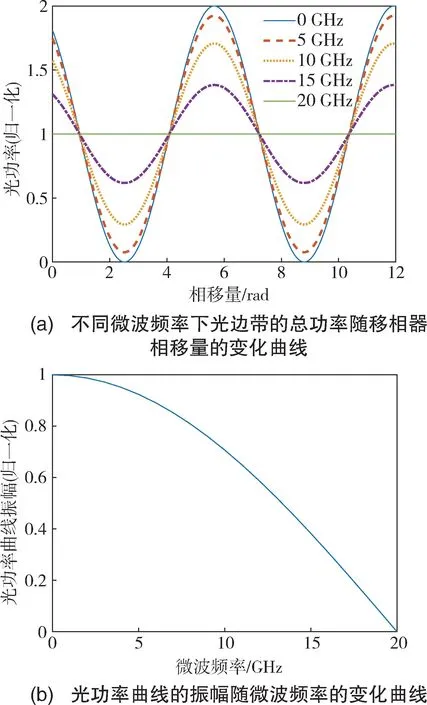
图6 光电探测器光边带总功率随移相器相移量的变化曲线及其光功率振幅随微波频率变化趋势图Fig.6 Variation curves of photodetector total optical sideband power with phase shift of phase shifter and variation trend of optical power amplitude with microwave frequency

由图7可知,若待测微波频率在0GHz～20GHz范围内,通过两路光电探测器测得归一化光功率曲线振幅,MZI滤波器1随调制微波频率的变化是一条从1降到0的平滑曲线,而MZI滤波器2随调制微波频率的变化是一条规律波荡曲线,微波频率在4GHz内出现一个波谷,且波形完全相同。工作频率范围内的低频和高频微波的频率对测量精度有很大影响,频率越高,其精度越低。

图7 FSR分别为80GHz和8GHz时两路频率测量链路测得的光功率曲线振幅随调制微波频率的变化Fig.7 Variation of optical power curve amplitude measured by two frequency measurement links with modulated microwave frequency when FSR is 80GHz and8GHz respectively

图8为到达角的振幅统计图。从建模仿真实验数据得出,若待测微波频率在0GHz～20GHz范围内,则通过MZI滤波器1测得的到达角曲线振幅落在1上下,而对于MZI滤波器2测得的到达角曲线振幅落在0～1之间,从而大幅提高了频率测量的精度。通过增大MZI的两臂长度差,可以进一步减小MZI滤波器2的FSR,随着其FSR的减小,测得的到达角曲线振幅区间就越小,对应测得的频率就越准确,从而进一步提高了测量精度。

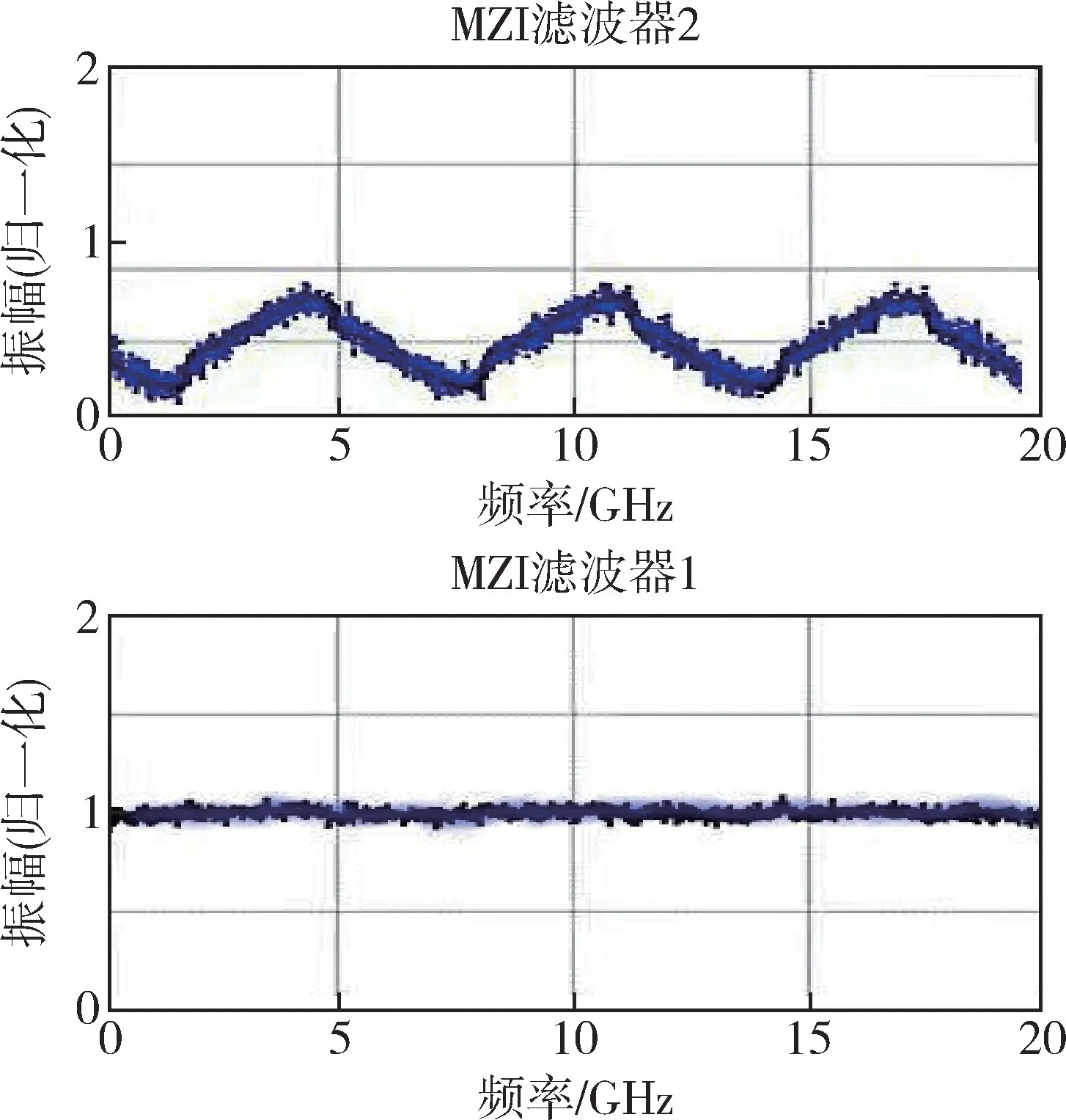
图8 到达角的振幅统计Fig.8 Amplitude statistics of angle-of-arrival

4 结论

本文提出了一种基于载波抑制双边带调制和MZI结构的集成光子辅助微波频率和到达角测量方案,实现了同时对微波频率和微波到达角的测量。通过控制MZI滤波器将微波频率信息映射到光功率变化的振幅,测量微波信号的频率;通过MZI干涉仪结构将相位差映射到光功率,通过光电探测器可以对两路信号的相位差进行测量,根据频率和相位差可以计算得到微波信号的到达角。此方案避免了传统微波测量仪器电路复杂、测量频率带宽不足的缺点,设计的MZI结构集成光子测频方法对各光学处理器件要求也不高,避免了复杂的测量构件。该方法易于实现,具有广阔的应用前景。