典型精密零件坐标测量不确定度的优化评定与验证

郭小冬,王明海,郭 猛,张 荣,翁汉旺

（北京航天控制仪器研究所,北京 100039）

0 引言

测量不确定度表征测量结果的可信性。对于高精度零件的测量,由于测量仪器的精度裕量小,环境因素的影响大,测量结果的可信性问题更为突出。由于坐标测量机（Coordinate Measuring Machine,CMM）误差的复杂性和功能的多样性,使得其面向任务的测量不确定度的评价比较困难［1］。

近年来,随着技术研究的深入,评价CMM测量不确定度的理论和方法不断被提出。陈晓怀、程银宝等［1-3］系统研究了CMM面向任务的测量不确定度的评定方法。Štrbac等［4］分析了CMM平面度测量不确定度评价时测量不确定度表示指南（Guide to the Expression of Uncertainty in Measurement,GUM）法与ISO/TC15530-3方法之间的差异。Vrba等［5］研究了复杂曲面CMM测量不确定度评定的不同方法。张学仪等［6］研究了采用蒙特卡洛法（Monte Carlo Method,MCM）进行叶片型面参数测量不确定度分析的方法。Rost等［7］研究了齿轮测量仪面向任务的测量不确定度MCM评定方法。Miura等［8］研究了采用MCM评定孔板测量不确定度的方法。但对于在实际不确定度评定中时常出现的因过量估计导致不确定度评定结果偏离实际情况乃至失准的问题,业内研究成果较少。

为此,本文以动压马达半球零件球径测量不确定度的评定为例,针对造成过量估计的两个主要原因——CMM示值误差的过量估计以及常规GUM法对被测量分布类型的正态分布保守假设进行分析,研究了采用标准工件进行测量标定获得CMM实际示值误差的不确定度优化评定方法以及采用MCM对GUM法的评定结果进行验证,发现并纠正GUM法假设偏差的不确定度验证方法,以期提高不确定度评定结果的可靠性。

1 不确定度的常规评定

关于面向任务的CMM测量不确定度评定,目前已有行业内认可的研究成果［1-3］,即利用测量系统分析（Measurement System Analysis,MSA）量值统计分析的方法,将CMM测量时主要不确定度来源提炼、归纳为示值误差、重复性误差、复现性误差以及温度补偿误差4项,进而建立不确定度评定模型并给出各不确定度分量的量化方法,最终按GUM法［9］完成测量不确定度的评定。本文的CMM尺寸测量不确定度的常规评定参照文献［1］提出的方法进行,具体如下:

1.1 不确定度评定模型

CMM尺寸测量误差分析模型为

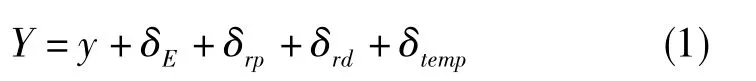
式（1）中,Y为被测量,y为被测量的估计值,δE为示值误差,δrp为重复性误差,δrd为复现性误差,δtemp为温度补偿误差。

假设δE、δrp、δrd和δtemp相互独立,基于方差合成定理,得到的不确定度评定模型为

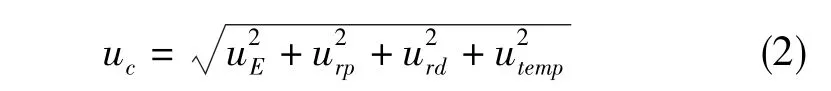
式（2）中,uc为合成标准不确定度,uE为示值误差引入的不确定度分量,urp为重复性引入的不确定度分量,urd为复现性引入的不确定度分量,utemp为温度补偿引入的不确定度分量。其中,utemp又可细分为uT、uCTE1、uCTE2三个分量,uT为温度变化引入的不确定度分量,uCTE1为工件线膨胀系数变化引入的不确定度分量,uCTE2为CMM光栅尺线膨胀系数变化引入的不确定度分量。utemp可表示为

1.2 不确定度分量的量化

各不确定度分量按表1所列公式进行量化。

表1中,MPEE=A+B·L为CMM最大允许示值误差（A为常数项,B为线性系数,L为被测长度）,n为测量次数,m为测量组数,yi为n次重复测量中某一次的测得值,y-j为m组测量中某一组的平均值,y-为组内平均值,y=为组间平均值,L为被测尺寸,T为环境温度,αW为工件线膨胀系数,αM为CMM光栅尺线膨胀系数。

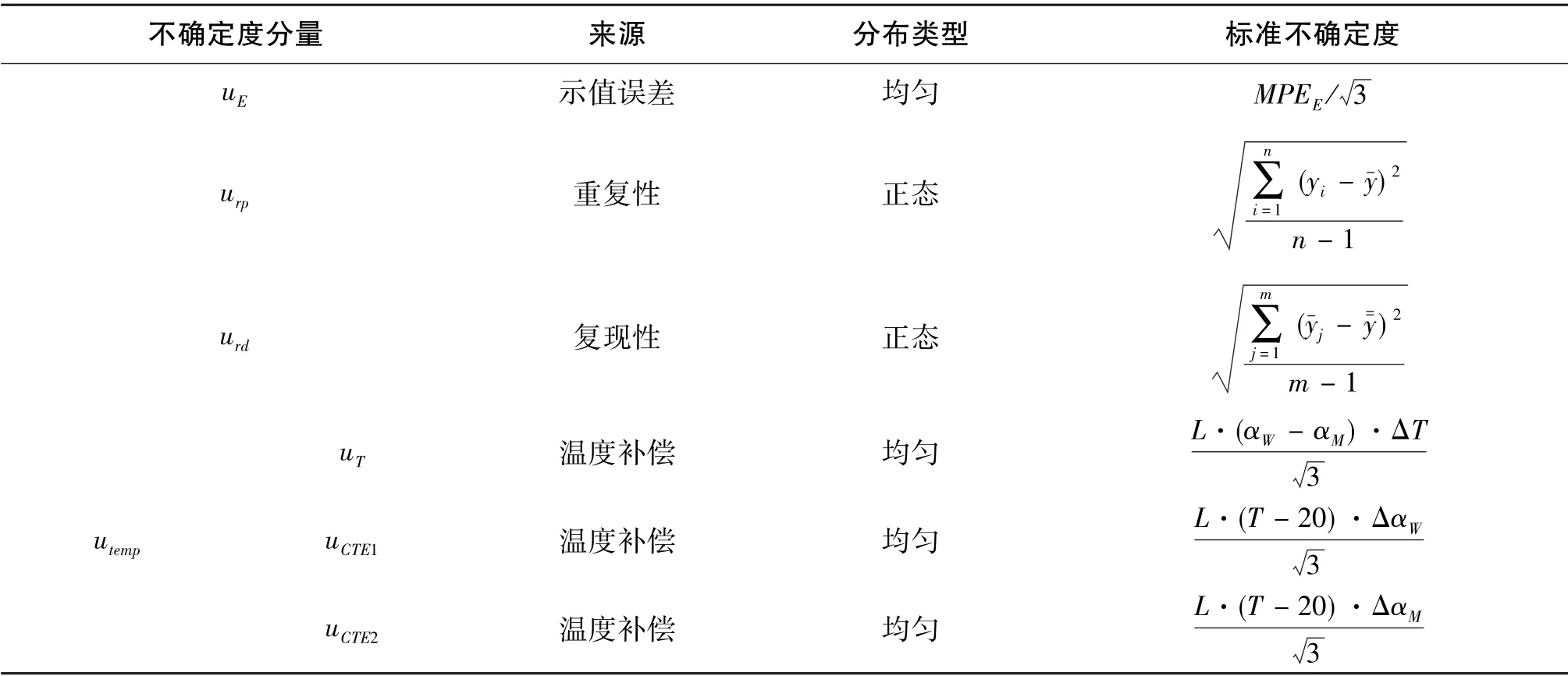
表1 测量不确定度分量汇总Table1 Summary of uncertainty components

1.3 合成标准不确定度uc的计算

按照式（2）进行计算,可得合成标准不确定度uc的值。

1.4 扩展不确定度U的计算

式（4）中,k为包含因子。依据GUM,包含概率p=95%时,k=1.96。

1.5 评定实例

在温度条件为20℃±1℃的测量间内,使用Leitz PMM866p坐标测量机对动压马达半球零件的球径进行测量。零件的标称直径SΦ为15mm,公差为2μm;CMM的最大允许误差指标为MPEE=（0.8+L/600）μm;工件的线膨胀系数为αW=（12.01±0.57）×10-6/℃,CMM光栅尺的线膨胀系数为αM=（10.5±1.0）×10-6/℃。半球零件图及测量实景如图1所示。

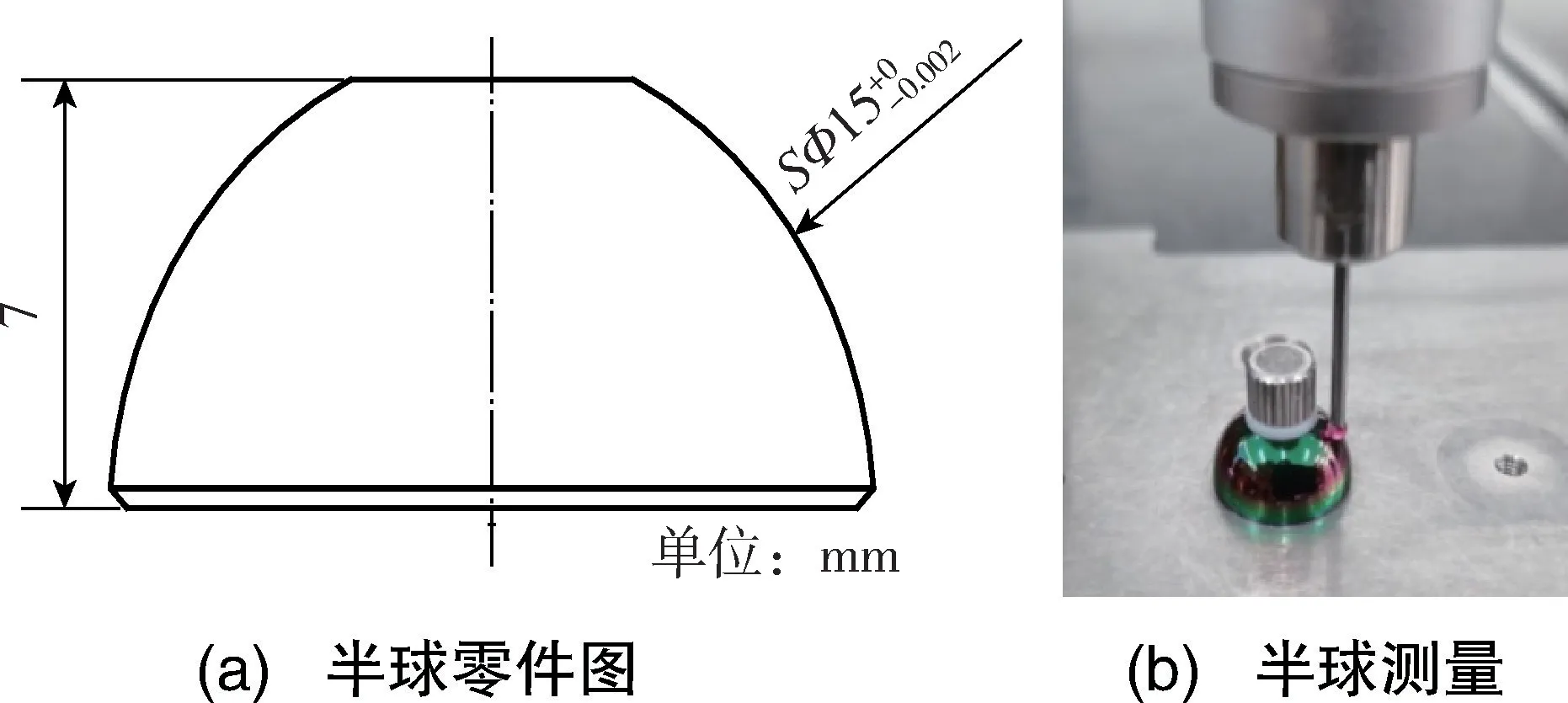
图1 半球零件图及测量实景Fig.1 Hemispherical part drawing and measurement real scene

为减小复现性误差,将测量策略（探针规格、采点方式、拟合方法、装夹方式等）作了统一规定。由不同操作者在不同时间段对同一半球零件的直径进行了20组重复测量,每组测量10次,测量数据如表2所示。

1.5.1 计算各不确定度分量

1）示值误差引入的不确定度分量uE

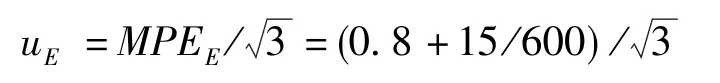
=0.825/3=0.476μm

2）重复性引入的不确定度分量urp

任选表2中20组数据里的一组考察重复性（本次分析选第3组数据）。按表1中对应公式计算urp,可得urp=0.066μm。

3）复现性引入的不确定度分量urd

根据表2所列20组数据,按表1中对应公式计算urd,可得urd=0.183μm。

表2 半球直径测量数据Table2 Measurement data of hemispherical diameter

4）计算温度补偿误差引入的不确定度分量

将温度、温度变化、工件线膨胀系数及CMM光栅尺线膨胀系数代入表1中对应公式进行计算,可得uT=0.013μm、uCTE1=0.005μm、uCTE2=0.009μm,再按式（3）计算得到utemp=0.017μm。

1.5.2 计算合成标准不确定度uc

将以上各不确定度分量值于表3中汇总列出。

将表3中各分量的标准不确定度值代入式（2）,可得uc=0.514μm。

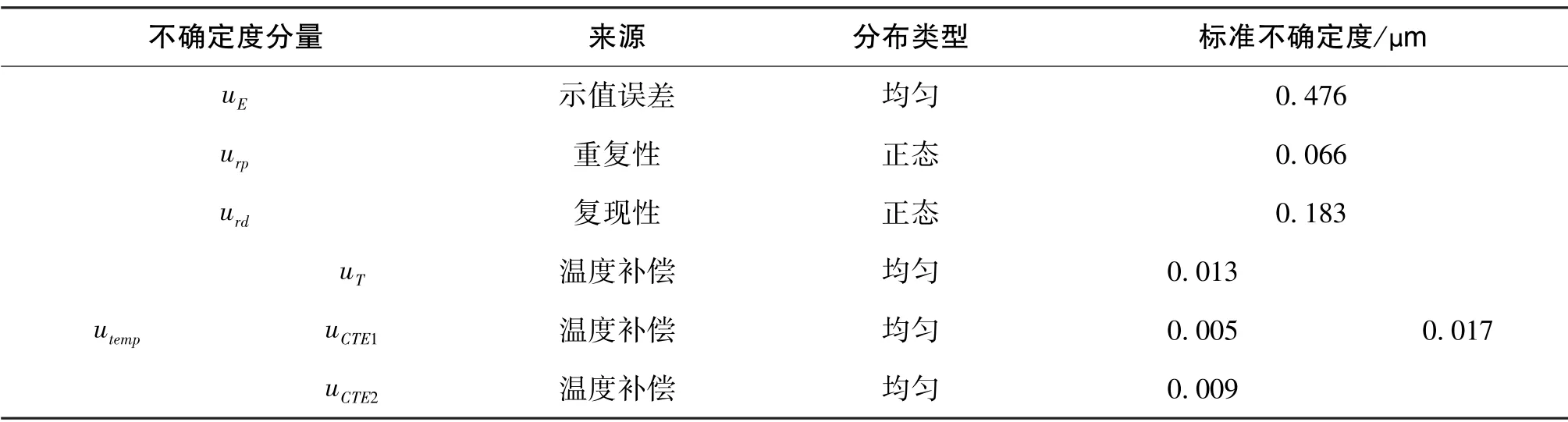
表3 常规评定不确定度分量量值汇总Table3 Summary of conventional evaluation uncertainty components

1.5.3 求扩展不确定度U

按照式（4）进行计算,可得U=kuc=1.96×0.514=1.01μm。

2 不确定度的二次优化评定

1.5小节中按常规评定的球径测量不确定度为U=1.01μm,已超过2μm公差值的1/3,即U＞UT=0.67μm（UT为目标不确定度［10］,UT=T/3,T为公差）。按精度分配原则［11］,测量能力不满足工艺要求。同时,用本文将要介绍的MCM进行不确定度验证也未能通过。为此,对评定过程进行重新审视。由表3可知,各不确定度分量中,示值误差分量uE的占比最大,对评定结果有显著影响。常规评定时,uE是按CMM的最大允许误差指标MPEE进行量化的,很可能存在过量估计。于是,采用使用标准工件的方法对PMM866p CMM进行针对性的示值误差标定,即使用经上一级计量标准——0.3μm精度等级的超精密CMM校准的同规格半球进行示值误差标定,得到实际的示值误差,进而对不确定度进行二次优化评定。

标准半球的直径校准值为ycal=14.99930mm,校准不确定度Ucal95=0.20μm（k=1.65）,则其标准不确定度ucal=0.20/1.65=0.12μm。

在PMM866p CMM上对标准半球的直径进行测量,测得值为y=14.99938mm,实际示值误差为E=y-ycal=0.08μm,优化后的示值误差不确定度分量为uEO=E/3=0.08/3=0.046μm。

优化后的不确定度分量如表4所示（urp、urd、utemp的值不变）。

表4 优化评定不确定度分量量值汇总Table4 Summary of optimized evaluation uncertainty components

对不确定度首次评定中发现的最大（占优势）的不确定度分量重新定制量化方案,得到其更准确的上界估计值［10］,进而进行二次评定,通常可显著降低过量估计的影响。

判据为

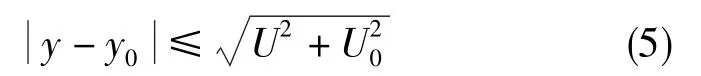
式（5）中,y为本级计量标准的测量结果,y0为上一级计量标准的测量结果,U为本级计量标准测量结果的扩展不确定度,U0为上一级计量标准测量结果的扩展不确定度。

如式（5）成立,则验证通过［12］。

对上文所述球径测量不确定度的评定结果进行传递比较法验证,上一级计量标准为0.3μm精度等级的超精密CMM,验证数据如表5所示。

表5 传递比较法不确定度验证数据Table5 Uncertainty verification data of transfer comparison method

3 不确定度验证

3.1 传递比较法

依据JJF1033,应优先采用传递比较法,通过与上一级计量标准的测量结果比较,验证测量不确定度评定的合理性［12］。

验证结果:使用传递比较法,两种评定方法评定的测量不确定度均验证通过（包括过量估计的常规评定结果）。

传递比较法的局限性:验证是单向的,即只能验证给出的不确定度是否偏小,不能验证是否偏大。对于过量估计的检验,该方法并不适用。

3.2 蒙特卡洛法

3.2.1 简介

蒙特卡洛法（MCM）通过计算机对各影响量进行大量的随机抽样,并通过对大量的抽样值进行数值计算来评定测量不确定度。GUM法对不确定度分量合成后输出量的分布类型假设为正态分布,但实际的情况并非总是如此。MCM的“海量”随机数模拟的结果能够反映输出量分布的实际情况,直接得到扩展不确定度。因此,可以以MCM的结果作为标准,去验证GUM法得出的扩展不确定度是否正确。

3.2.2 模拟方法

对于误差分析模型Y=y+δ1+δ2+…+δn,首先对每个误差分量（δ1、δ2、…、δn）按给定的分布类型和分布区间进行M次随机模拟抽样,各自产生M个随机数,然后对各误差分量的M个随机数进行代数和相加,得到M个测量误差Δy的合成样本值,再按式（6）及式（7）计算平均值和标准不确定度uc,并按给定的包含概率p%计算包含区间,所得包含区间的半宽即为扩展标准不确定度U。

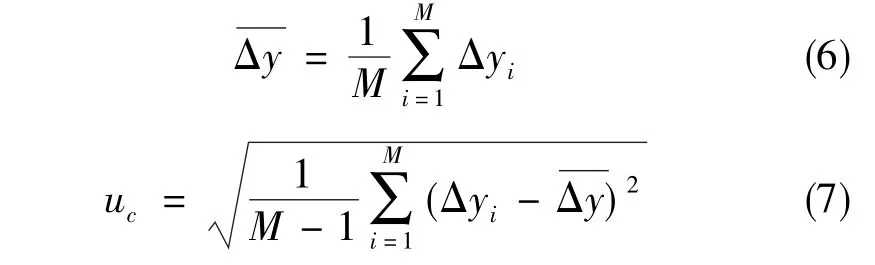
试验次数的选择:试验次数越多,不确定度评定失真就越小,但试验次数越多,需要的计算时间也越长。可以采用自适应算法自动选择足够的试验次数,以保证模拟的可靠性。在自适应MCM程序的执行过程中,试验次数不断增加,直到所需要的、uc、具有指定包含概率的包含区间端点Δylow和Δyhigh等4个结果达到统计意义上的稳定（2倍标准差小于标准不确定度要求的数值容差δ［13］）。在采用自适应MCM对GUM法进行验证时,以δ/5作为稳定性判断阈值［13］。

数值容差δ［13］:将标准不确定度的数值表示为c×10l的形式,c为ndig个有效十进制整数,l是整数,则数值容差为

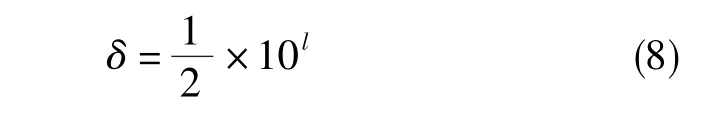
3.2.3 验证方法

GUM法获得的包含区间为［Δy-U,Δy+U］,MCM获得的包含区间为［Δylow,Δyhigh］。对这两个包含区间进行比较,确定两个包含区间的各自端点的绝对偏差dlow和dhigh

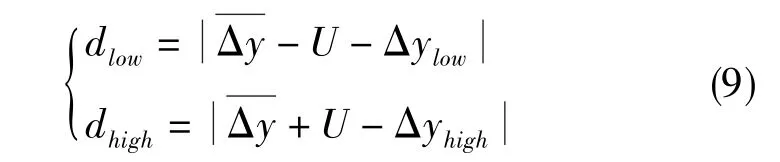
如果dlow和dhigh均不大于数值容差δ,则GUM法不确定度评定结果通过验证［13］。3.2.4 MCM应用实例

对1.5节所述球径不确定度常规评定的结果用自适应MCM进行不确定度验证。

1）算法

用Matlab软件编制自适应MCM程序。根据式（1）,分别对δE、δrp、δrd、δT、δCTE1、δCTE2按给定的分布类型和分布区间（δE～U（-0.825,0.825）,δrp～N（0,0.0662）,δrd～N（0,0.1832）,δT～U（-0.023,0.023）,δCTE1～U（-0.009,0.009）,δCTE2～U（-0.015,0.015））进行随机模拟抽样,生成6维大样本随机数,再将该6维随机数的各样本值代数和相加,得到球径测量误差Δy样本值、uc以及95%概率包含区间。（Δy=δE+δrp+δrd+δT+δCTE1+δCTE2）,进而计算

因标准不确定度保留2位有效数字,按式（8）计算数值容差δ=×10-2=0.005μm,自适应确定试验次数时,按e=δ/5=0.001μm确定稳定性判断阈值。

自适应计算控制:设定基本试验次数M=1×104［13］,在输入量的概率分布中,首先进行1×104次抽样并计算结果;随后进行第2次1×104次抽样并计算结果,样本量与前一次相迭加;结合前两次的计算结果,计算相关的标准差,若这些标准差均不大于e=0.001μm,则认为所有计算已达稳定,否则重复进行抽样计算,直至计算结果稳定。

算法程序流程图如图2所示。

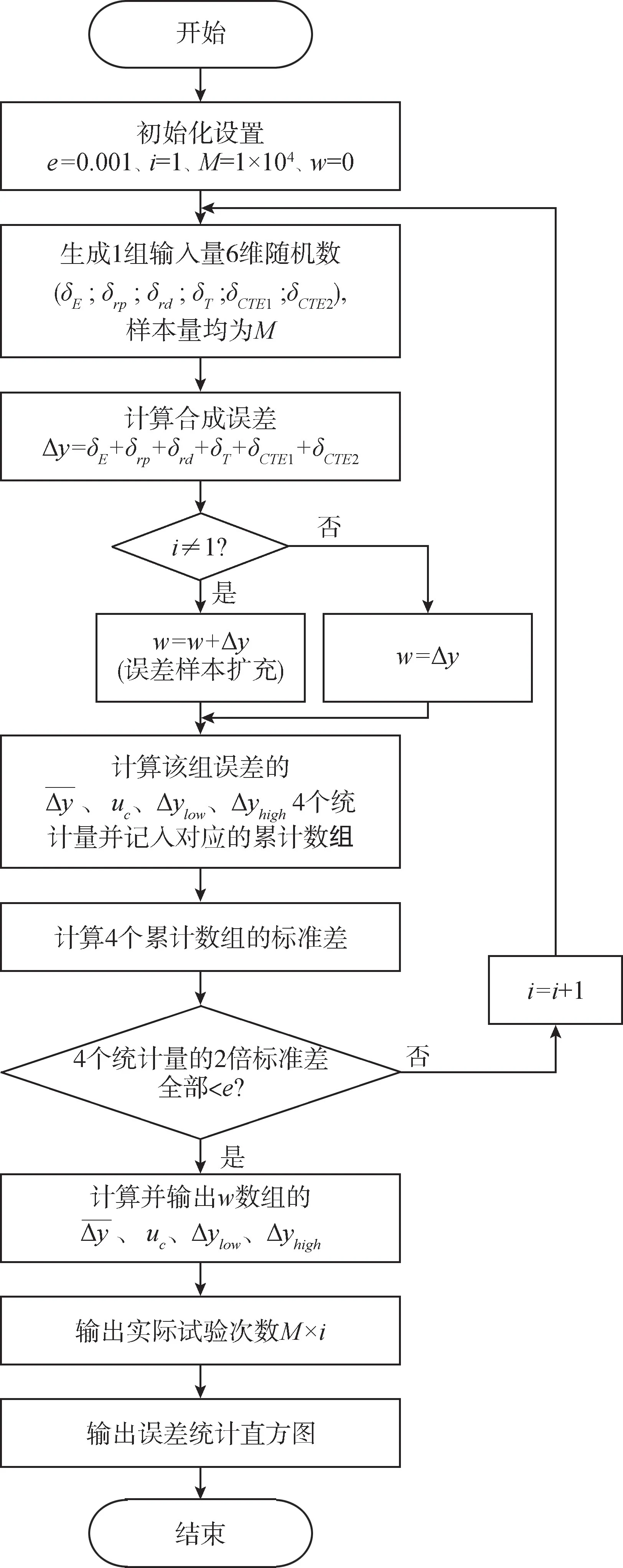
图2 自适应MCM算法流程图Fig.2 Flowchart of adaptive MCM algorithm

2）计算结果

MCM实际试验次数为2.70×106,=-0.0001μm,uc=0.5147μm,95%概率包含区间［Δylow,Δyhigh］=［-0.9147,0.9141］。

根据包含区间,可得扩展不确定度为U=0.9144μm≈0.914μm,包含因子为k=U/uc=0.9144/0.5147=1.78,输出的误差统计直方图如图3所示。

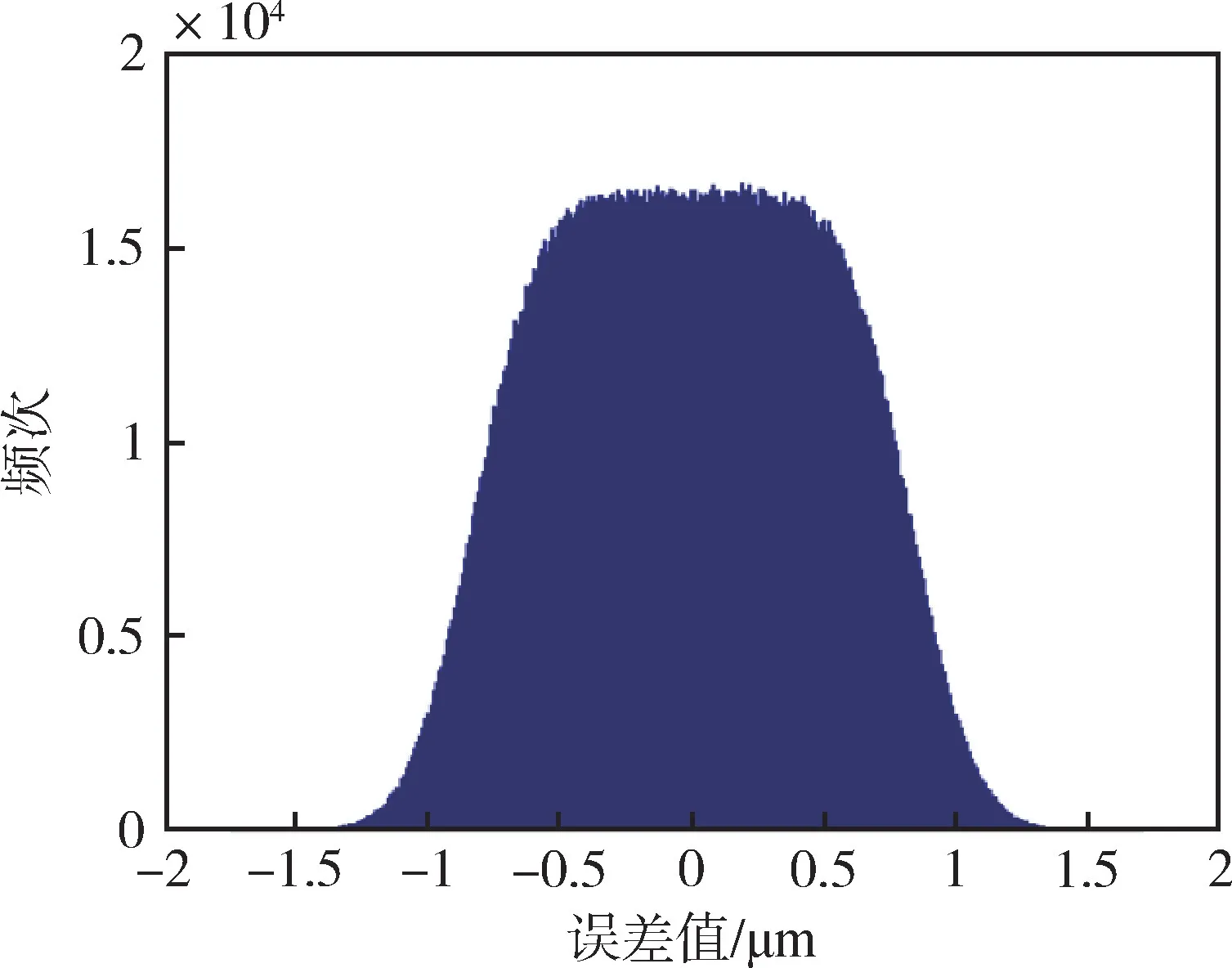
图3 常规评定误差统计直方图Fig.3 Error statistical histogram of conventional evaluation

根据表6所列数据进行验证:dlow=|-1.007-（-0.915）|=0.092＞δ=0.005,dhigh=|1.007-0.914|=0.093＞δ=0.005,故验证未通过。

表6 GUM与MCM常规评定结果对比Table6 Comparison of conventional evaluation results between GUM and MCM

原因分析:从统计直方图（图3）上看,分布图形已不是正态分布,而是近似的梯形分布,已明显偏离GUM法正态分布的假设。回看表3,占比最大的不确定度分量uE是均匀分布,但uE还没有大到成为占优势的分量［14］,第二大分量urd为正态分布,两者共同作用的结果造成合成后的分布似均匀非均匀、似正态非正态。

扩展不确定度应以MCM计算的结果为准,即U=0.91μm（k=1.78）。而GUM法的评定结果为U=1.01μm（k=1.96）,比实际情况扩大了10.2%。

同理,对第2章所述优化评定结果进行MCM验证,得到的数据如表7所示,验证能够通过的原因就是不再有大占比的非正态分布分量（表4）。根据中心极限定理［14］,合成后的分布近似正态分布。对此,图4所示的统计直方图也有直观的显示。

表7 GUM与MCM优化评定结果对比Table7 Comparison of optimized evaluation results between GUM and MCM

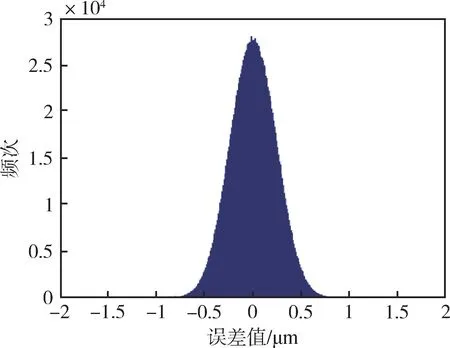
图4 优化评定误差统计直方图Fig.4 Error statistical histogram of optimized evaluation

可以得到dlow=dhigh=0.001＜δ=0.005,故验证通过。

示值误差的分布类型为均匀分布,示值误差的过量估计往往使其成为不确定度分量中的优势分量或近优势分量,从而使合成分布偏离正态分布,此时的MCM验证不能通过,故MCM验证可以作为是否存在示值误差过量估计的检验手段。

4 结论

针对示值误差过量估计导致不确定度评定结果偏大乃至失准的问题,本文研究了采用标准工件进行测量标定获得CMM的实际示值误差的优化评定方法,科学、合理地减小了不确定度。典型精密零件——动压马达半球球径测量不确定度评定结果表明,采用优化评定法后,不确定度由常规评定的1.01μm减小为0.46μm,降幅达54.5%。评定结果U=0.46μm＜UT=0.67μm（目标不确定度）,证明测量能力能够满足工艺要求。本文研究了采用自适应MCM对GUM法评定结果进行验证的方法,MCM可以发现并纠正被测量偏离正态分布时GUM法的正态分布假设造成的过量估计,减小了不确定度。半球球径测量MCM仿真验证的结果表明,GUM法常规评定的不确定度比实际情况扩大了10.2%,传统的不确定度验证方法——传递比较法并不能解决过量估计导致的不确定度偏大的验证问题。然而,示值误差的过量估计会使被测量偏离正态分布,对此MCM验证是敏感的,故MCM验证可以作为示值误差过量估计的检验手段。本文的研究成果对于提高精密零件坐标测量不确定度评定结果的可靠性具有实际意义。