解实正定线性方程组的交替方向迭代法新格式
征道生
(华东师范大学 数学科学学院, 上海 200241)
0 引 言
设M=(mi,j)∈Rm×n为实矩阵, 当m=n且M是正定 (半正定) 时, 称M为p.d. (p.s.d.). 令t=j-i, 元素集lt={mi,j|j-i=t}称为M的第t根对角线. 当lt中的元素都异于0 时, 也称该对角线是M的链. 如果M恰有q条非零对角线, 则称其为q-对角线的.
设p≥0 ,q≥0,p+q ∈N+, 若l−p和lq均为非0 对角线, 且当j-i<-p或j-i>q时, 均有mi,j=0, 则称M是具有左半带宽p和右半带宽q的带状矩阵(若p=q则称M具有半带宽p), 此时称集合Sb={mi,j|q≥j-i≥-p}为M的带区.
如果M为块对角矩阵, 且每个对角块都是q-对角的, 则称M为广义q-对角阵.
当M恰有h条非零对角线lt1,lt2,··· ,lth, 且gcd (t1,t2,··· ,th)=s, 则称s=span(M) 为M的跨度. 称线性方程组

是rspde, 是指M为实正定矩阵.
设式(1)是rspde, 如果在Matlab 中, 有
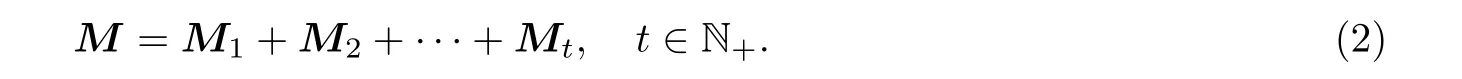
式(1)中: 每个Mi都是半正定, 且其中有一个为正定的, 就称M分裂成t个方向矩阵之和, 且称式(2)是M的一个方向矩阵个数为t的交替方向迭代分裂(简记为adist). 进一步, 如果诸方向矩阵满足条件

则称式(2)为一个可交换分裂(简记为cadist), 否则称为ncadist.
对于t=2 , 利用式(1)和式(2)以及迭代参数rk>0 , Peaceman 等[1]所建立的交替方向迭代(ADI)的PR 格式为

对于t=3 , Douglas 等[2]建立的DR 格式为
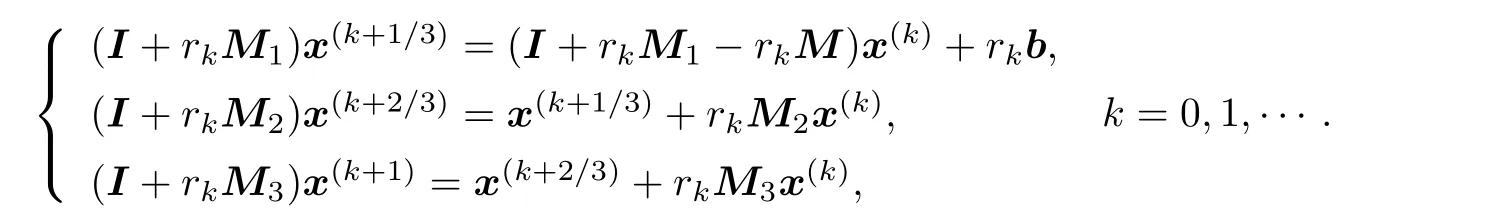
记迭代格式中的误差向量为
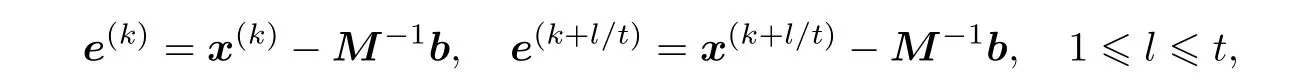
则用迭代格式可推出相应的误差向量的传播方程为

另一方面, 尽管ncadist的算例广泛存在, 但至今似乎仍缺少建立收敛的ADI 格式的相应信息. 出现这一令人遗憾的局面之原因在于, 人们只顾笼统地控制误差e(k), 却忽略了对e(k+l/t)的仔细分析.事实上, 因为对于ncadist来说, 此处Tk是非对称的, 所以其谱半径ρ(Tk) 较难估计.
为了分析迭代子步的误差传播, 需要先确定某种迭代格式. 以t=3 为例, 从式(1)和式(2)出发, 令

则Nl也是半正定的. 考虑一种修改的ADI 格式(RADI):

其误差传播方程为

这里

虽然Tk,l一般也不对称, 但它是两个Hermite 矩阵之积, 因而其谱半径满足不等式

适当选择r, 可保证

定理1 是本文的第一个重要结论, 它避开了方向矩阵的可交换条件(式(3)), 使迭代格式(式(5))有了广泛的可用范围, 从而使不少原来不便于使用ADI 的实际问题成了ADI 应用的新对象 (见第3 章).
事情的另一面是, 一个收敛的RADI 未必是受欢迎的. 这就必须考虑收敛格式的效率, 也就是与格式相关算法的效率. 与ADI 格式效率有关的因素包括:
(i) 加速参数r的选择;
(ii) 迭代第k步及其迭代子步的计算复杂性;
(iii) 算法的耗时值, 在Matlab 中表示为elapsed-time;
(iv) 算法的并行性等.
其中, 因素(ii)与迭代子步的各个系数矩阵I+Ml的稀疏性有极大关联. 传统的ADI 格式的一大优点是往往能保证这些系数矩阵是三对角的, 从而能在用消元法解迭代矩阵方程时由极少次数的运算完成.
对于效率欠佳的RADI 格式, 有时经过改进也可成为高效格式. 比如,Ml不是三对角的, 但它有分解式Ml=W1+W2+···+Wlh, 而其等式右边有三对角矩阵. 这就是所谓的再分裂技巧(见本文第3 章).
1 预备知识
引理 1[4-5]下列关于n阶方阵的各命题是等价的.
(1)M是正定(半正定)的;
(2) 对每个非零x ∈Cn,xTMx>0(≥0) ;
(3)M酉相似于正(非负)对角矩阵;
(4)M是Hermite 的, 且其特征值均为正(非负);
(5) Hermite 矩阵M的n个顺序主子式皆为正(非负);
(6)M−1是正定的.
引理 2 设M ∈Cn×n是正定矩阵,W,N ∈Cn×n是半正定矩阵,c>0 . 则:
(i)cM是正定的;
(ii)M+W是正定的;
(iii)∀l ∈N,Ml是正定的;
(iv)W+N是半正定的.

引理6 也被称为可逆方阵逆矩阵的秩t修正定理.
这里对方程组

的解法做一些说明. 当Ml半正定, 且r≥0 时, 式(6)的系数矩阵是正定的. 右端项需由矩阵乘法及加法算得. 假定Ml+Nl=M ∈Rn×n为 2t+1 对角的, 1 获得解x=M−1b. 这需用大约 5n次四则运算. 从具体算例易见, 在G为 2t+1 对角阵, 且t>1 时, 如果M的半带宽为 1 当G为三对角阵时, 并行算法对式(6)也颇具吸引力, 但并行算法针对不同情况需做不同的附加准备. 以两个n维向量u,v作内积为例, 第一个并行操作可算出 (6) 记gl(r)=gm,l(r)gn,l(r) , 有 0 (7) 在每个迭代子步中, 且 意味着对任给的 , 有关系式 证 明 略去(1)—(4)的证明. 说 明 (1) 在定理1 中未曾用到条件(3)(式(3)). (2) 定理1 证明了在每个迭代子步中, 误差向量e(k+(l−1)/t)的2-范数被压缩了gl(r) 倍, 这是一个粗略的估计. 更恰切的压缩因子应当是 (3) 从定理1 的证明中, 可看到式(4)中的每个迭代子步都在压缩迭代误差向量. 于是有定理2. 定理 2 如果将定理1 中所用的式(4)改为 则有 这就是回归单方向迭代技巧, 其优点之一是可以简化计算格式. 事实上, 当Ml0为三对角阵, 其他Ml有更复杂结构时, 式(10)显然更可取. 实际数值算例也证明了这一点. 在定理1 中, 考虑优化加速收敛参数r时, 用到一个事实:‖Nl(r)‖2≤‖Nl(r)‖∞. 这使得在实际估算ru,l时较为方便. 参见方程(15)和(16). 在交替方向迭代中可以发现, 并行计算能发挥独特的作用. 下面先就实正定三对角方程组 于是 其中 这表明, 引理6 导致了升阶式(13). 也就是当两个低阶方程 Rspde 的一个重要来源是各种数学物理边界值问题的相应离散逼近线性方程组, 本章将介绍其中几个, 先给出以下两个定理. 证明从略. 下面对5 个实际问题建立相应的离散逼近方程[7]. 例 1 二维调和方程边值问题 式(15)中:∂D为区域D的边界, 第2 个等式被称为边界条件. 例 2 三维调和方程边值问题 例 3 三维非长方体域上调和方程边值问题 例 5 三维变系数椭圆型方程边值问题 由此可知 当fxx,fyy连续时, 可考虑式(15)的O(h4) 离散逼近方程[7] 和一个adis3 式中:W3的分块形式为 易知Wl是三对角的, 1 ≤l≤4 . 这时再用式(5)和(25)来解方程(23), 便保持了ADI 的良好传统. 这就是再分裂技巧的好处. 当然, 对于方程(23), 如果用回归单向迭代技巧, 也可避免再分裂技巧的使用. 不过, 下文会遇到必须使用再分裂技巧的情况. 如果将式(25)中的Wl仍称为方向矩阵的话, 它与物理或几何上所说的方向似乎有差别了, 所以只能认为它是广义的方向. 对于截断误差为O(h4) 的式(23), 其数值结果自然应具有O(h4) 的数值精度, 因而对相同的步长h往往会有远高于由式(21)所得的相应结果. 具有截断误差O(h2) . 式(26)中:M的一个adis3 为 上式中:M1是一个有m2个对角块的块对角阵, 且每个对角块均为A, RADI 格式和DR 格式自然都可求解式(26), 回归单向技巧也可应用. 仿照例1, 可建立截断误差为O(h4)的式(16)的离散逼近方程, 并可应用再分裂技巧和回归单方向迭代技巧. 此处暂且略去有关细节. 记x=(x(1),x(2),··· ,x(s),··· ,x(n))T, 且 此时M有一个ncadis3 而Ml(1 ≤l≤3) 可由以下的Matlab 程序确定: 其中,Ml均为广义三对角正定矩阵. 式(27)是一个7 点格式, 且不满足式(3). 因而DR 不适用, 但可用RADI, 也可用回归单向迭代技巧. 在例4 中, 式(18)有一个截断误差为O(h2) 的离散逼近: M可分裂为一个adis3[7] 上式中:M1,M2,M3均为5 对角矩阵, 且M1,M2不是对角占优, 仅M3为对角占优. 由定理3,M3可再分裂为两个三对角阵之和: 这与式(24)的情况完全类似, 因为此处的M3是式(24)中的N3的2 倍. 于是可写成 由回归单向迭代法, RADI 也可用于式(28). 由于M1,M2不是对角占优, 因而不太可能将M再分裂,使每个方向矩阵都变成三对角阵. 利用引理2 可证,M1,M2,M3均正定. 实际上, 利用Matlab指令v=eig(M) 可算出M的n个特征值, 从而可验证M1,M2,M3的正定性. 在例5 中, 方程(19)有一个截断误差为O(h2) 的离散逼近 和一个ncadis3[6] Douglas Rachford Scheme (DRS)自然不适合于式(29), 但RADI 可用. 这里略去对Ml的详细描述. 本文的结果表明, 再分裂及回归单一方向迭代确实可以极大地扩大ADI 的可用范围, 而且有时可提高对具体应用对象的计算效率和精度. 3 点期望是: (i) 对RADI 的并行计算能够实现; (ii) 发现有别于RADI 且不受条件(3)(式(3))限制的高效API 格式; (iii) 寻找RADI 更多的高效应用对象. 致谢 作者对陈果良教授和王善平编审在本文的写作过程中给予的关心与帮助表示衷心的感谢.

2 收敛定理与回归单方向迭代格式

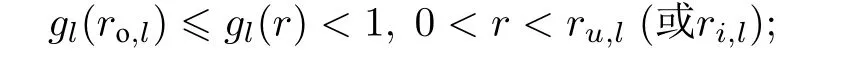



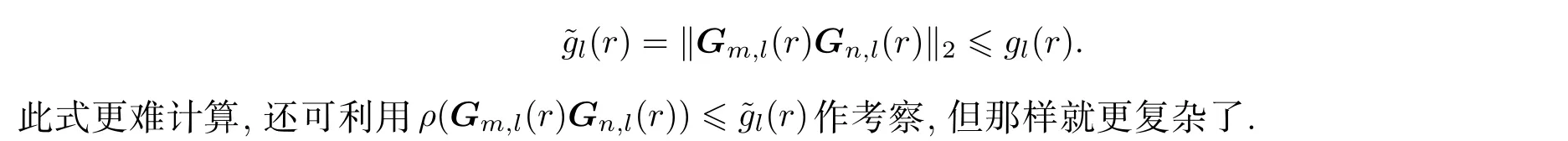




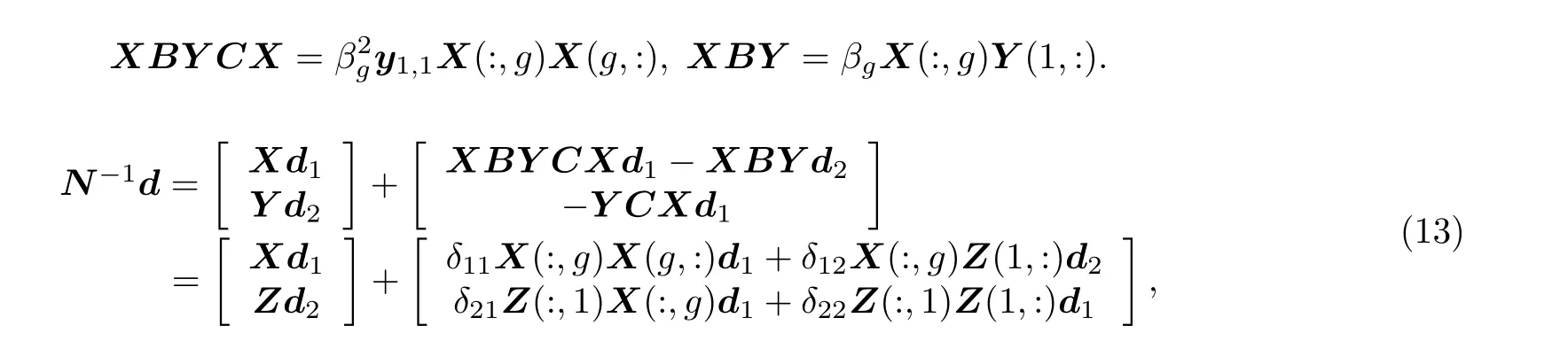


3 应 用


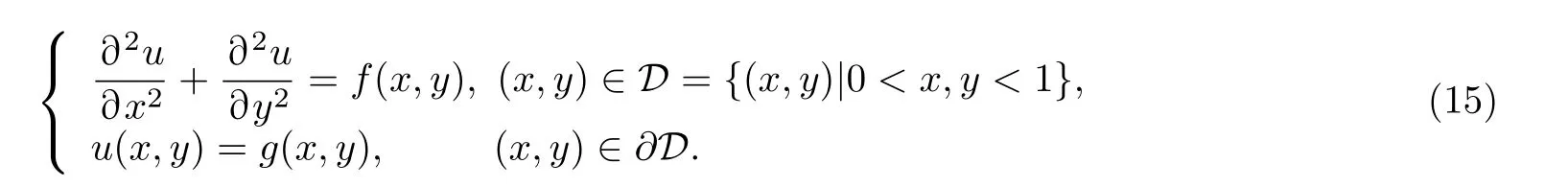
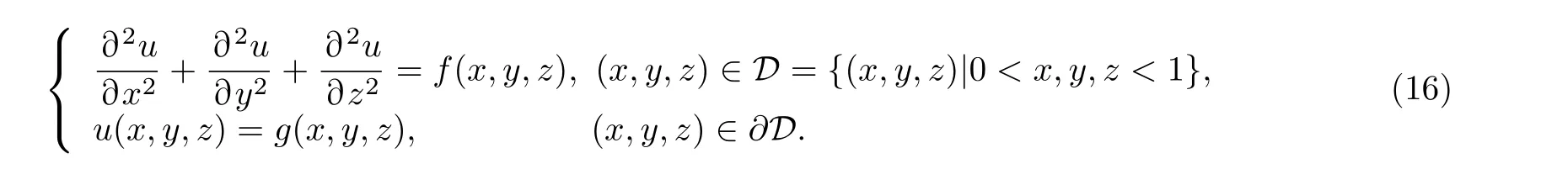
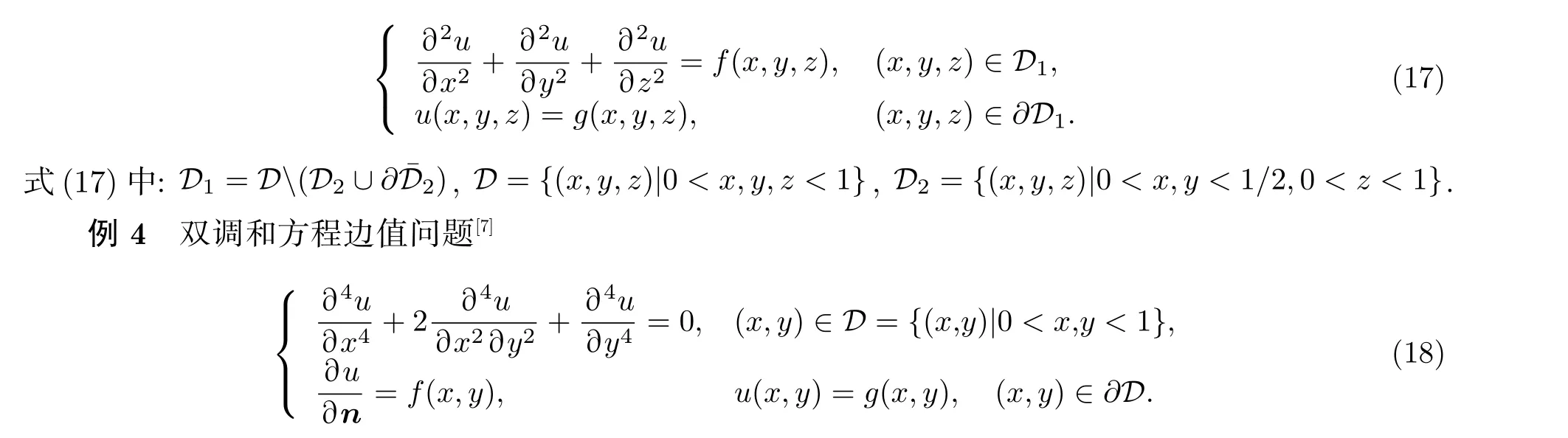

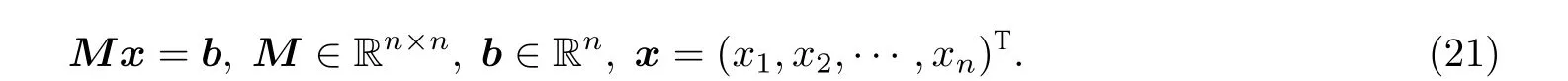






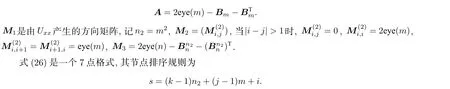

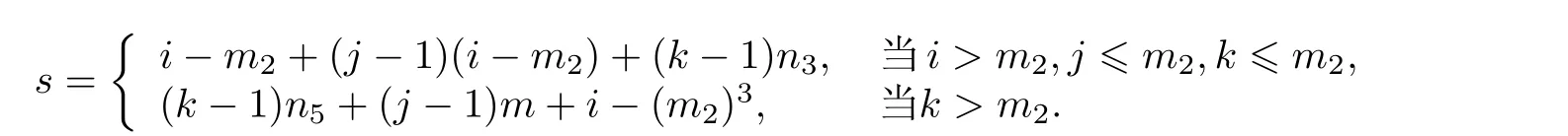




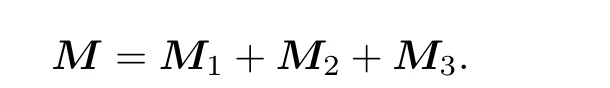
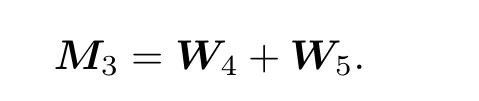

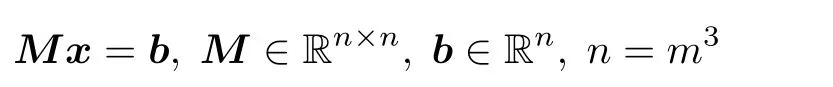

4 总 结

