(2 + 1)维Dirac 振子的Foldy-Wouthuysen 变换

孙 伟, 张可烨

（华东师范大学 物理与电子科学学院, 上海 200241）

0 引 言

为了使量子力学能够应用到高能物理和宇宙学等领域, 1928 年Dirac 提出了满足Lorentz 协变性的自由电子波函数演化方程—Dirac 方程, 并逐步建立了单粒子的相对论性量子力学. Dirac 振子是在此基础上, 结合量子力学中最常用的简谐振子模型而发展出来的相对论性量子力学中的一个常用模型, 经常被用于研究量子效应和原理的相对论性拓展, 如Dirac 猫态[1]、(1 + 1)维相对论性测不准原理的研究[2], 以及相对论性量子热机模型等[3].

Dirac 方程描述了1 个相对论性的自由粒子, 其哈密顿量和对应的本征能态中充满着自旋与动量自由度的耦合, 这给基于它的计算和测量造成了困难. 只有在弱相对论极限下, 其正反自旋才会被封闭于完全分离的正负能态中, 不再展示与动量的耦合, 十分便于计算. 随之而来的问题是, 能否找到1 个自旋与动量自由度在任何情况下都可以被完全分离的表象. Foldy 和Wouthuysen 在1950 年证明了对于自由Dirac 方程这个表象的存在[4]. 本文将关注点放到(2 + 1)维Dirac 振子的Foldy-Wouthuysen(F-W)变换[5]上. 从(2 + 1)维时空开始, Dirac 振子模型展示出了自旋与轨道角动量的耦合, 该模型是原子谱线、高能物理, 以及宇宙学研究中经常使用的模型. 本文不但推导出了可以简化其哈密顿量和本征态形式的F-W 变换, 还发现了自旋和轨道角动量算符在该变换表象中变成了极为复杂的耦合形式, 并证明了总角动量作为一个守恒量在F-W 表象变换前后其表达形式是不变的. 这些结果将加深人们对Dirac 振子的自旋-轨道耦合性质的认识, 而且本文发展的寻找F-W 变换矩阵的理论方法还可以应用到更复杂的相对论性量子系统上.

1 (2 + 1)维Dirac 振子模型

跃迁, 或者是

对于给定的量子数, 定义直积态

写成矩阵形式为

解得本征值为

相应的两个本征态为

其中, 归一化系数为

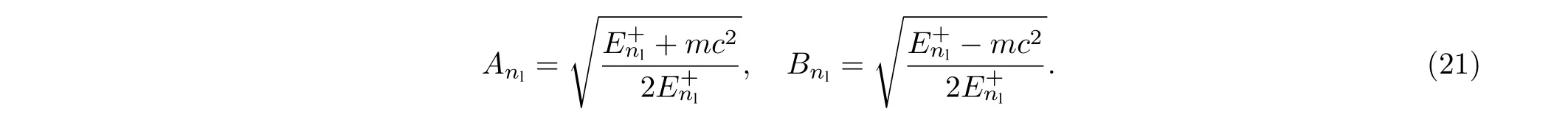
公式(20)中: |nl〉是左旋轨道角动量的Fock 态; |↑,↓〉是Pauli 自旋态.

2 (2 + 1)维Dirac 振子的Foldy-Wouthuysen 变换

Foldy-Wouthuysen (F-W)变换是一类能将Dirac 方程退耦合成2 个简单方程的幺正变换[10]: 一个方程描述正能态解; 另一个则描述负能态解. 从Dirac 振子的哈密顿量上考虑, F-W 变换的实质是将矩阵形式的哈密顿量对角化. 在标准表象下Dirac 振子的哈密顿量是1 个 2×2 的Hermitian 矩阵, 其缀饰态解 |〉是自旋态矢 |↑,↓〉和左旋轨道角动量态矢 |nl〉的纠缠态, 展示出自旋-轨道耦合效应. 本文通过F-W 变换, 可以干净利落地将自旋-轨道耦合效应分离, 使自旋态矢 |↑,↓〉和左旋轨道角动量态矢|nl〉分处于2 个独立的自由度空间, 其本征态也将变为位形态矢和左旋轨道角动量态矢直积的形式|nl〉⊗|↑〉或 |nl〉⊗|↓〉, 并将其称为F-W 表象下Dirac 振子的本征态.

图1 Dirac 振子的能谱(a)和归一化系数(b)Fig. 1 Energy spectrum of the Dirac oscillator(a) and normalization coefficient(b)

后续推导将用到玻色产生和湮灭算符的2 个重要对易关系[11]

3 Foldy-Wouthuysen(F-W)表象下的角动量算符

因此, 自旋算符在F-W 表象下的形式为

轨道角动量算符在F-W 表象下的形式为

总角动量算符在F-W 表象下的形式为

从上述结果可以看到, 尽管标准表象下的哈密顿量和本征态中的自旋-轨道耦合在F-W 表象下被解开, 但这并不意味着自旋-轨道耦合效应消失了. 这是因为自旋算符和轨道角动量算符在F-W 表象下的解析形式变成了标准表象下的自旋算符和轨道角动量算符的复杂组合; 或者说, 哈密顿量中的自旋-轨道耦合效应经过F-W 变换“转移”到了算符上. 另外, 总角动量算符在F-W 表象中的形式与标准表象中的形式相同, 这体现了其守恒量的性质.

尽管算符的自旋-轨道耦合形式十分复杂, 但如果考虑弱相对论和强相对论两种极限情况, 就可以获得相对简洁的形式. 在弱相对论极限下, 相对论参量满足ϵ →0 , 归一化系数近似为 |Anl|=1 和|Bnl|=0. 由此, 自旋算符表示为

轨道角动量算符表示为

其中, h.c.表示厄米共轭; 轨道角动量算符表示为

表1 展示了自旋算符和角动量算符在2 个表象(标准表象和F-W 表象)中的解析通式以及极限情况(弱相对论极限、强相对论极限)下的数学形式. 尽管强相对论极限中的自旋算符在形式上偏离但总角动量仍是这体现出了相对论性粒子的自旋内禀性.

表1 自旋算符和角动量算符在2 个表象的数学形式Tab. 1 Spin and angular momentum operator in the two representations

4 总结与展望

本文研究了以(2 + 1)维Dirac 振子为基本模型的F-W 变换: 首先通过缀饰态的方法求解了Dirac 振子在标准表象下的本征能量和本征态; 其次利用F-W 表象和标准表象基矢之间的变换关系得到了F-W 变换矩阵的具体形式, 然后通过F-W 变换将Dirac 振子的自旋-轨道耦合完全分离, 使其正能态和负能态分别与自旋向上和向下唯一相关; 最后讨论了自旋算符和角动量算符在F-W 表象中的具体形式, 以及弱相对论和强相对论极限情况下的近似情况, 并证明了总角动量作为一个守恒量在F-W 表象变换前后其表达形式都是不变的. 这些结果将使人们对Dirac 振子的相对论性本质有更深刻的认识; 而且本文发展的寻找F-W 幺正变换矩阵的理论方法, 还可以应用到其他更复杂的Dirac 量子系统上. 本文中的(2 + 1)维Dirac 振子模型, 不但可应用在与相对论效应有关的重力仪、时钟、加速器和量子传感器等新量子技术上, 还可以用来研究相对论性量子测量原理[14]、相对论性不确定性原理[15-16]等基础量子和相对论物理问题.