一种基于深层特征增强的多视图隐空间融合表征方法

郑婷一，吴嘉琪，张彬彬，王 莉

(1.太原理工大学 a.信息与计算机学院，b.大数据学院，太原 030024；2.山西能源学院 电气与控制工程系，山西 晋中 030600；3.新南威尔士大学，澳大利亚 悉尼 1466)

各行各业每天都在产生海量数据，从不同来源、结构或角度描述同一对象的数据称为多视图数据。以社交网络数据为例，某用户在不同网络平台上有推文、关注者、粉丝、评论等多视图数据，若对该用户的兴趣进行建模，需挖掘数据中隐含的丰富信息，学习用户多视图数据特征的统一表示，基于此再进行后续预测任务。多视图数据真正的价值不仅在于单视图具有独特性，而且视图间存在相关性、一致性和互补性[1]。

面对行业多视图数据的爆炸式增长，多视图学习变成一个非常必要且具有挑战的研究课题，该研究不仅在医疗诊断、多媒体计算、多传感器数据融合和人机交互等领域具有广泛应用价值，而且是当前机器学习的热点问题之一。一些传统的多视图学习方法为以学习视图间最大相关性为目标寻找潜在公共子空间，如：基于典型相关性分析(canonical correlation analysis，CCA)[2]的系列方法(多通道CCA[3]、聚积CCA[4]、标记多重CCA[5]等)。为提升数据融合性能，深度学习也加入到多视图相关性学习模型中，如：深度CCA(deep canonical correlation analysis，DCCA)[6]和深度广义CCA(deep generalized canonical correlation analysis，DGCCA)[7].这样做的优点是保留高维数据包含丰富信息，通过对原始数据投影变换，在尽可能多地保留原始数据结构和重要特征的前提下，学习原始数据的低维空间表示，解决数据维度灾难问题。为了进一步挖掘视图间一致性，一系列方法相继提出，如：Tri-training算法[8]、Co-forest算法[9]、Co-EM算法[10]、Co-regularization算法[11]和低秩稀疏分解方法[12]等。此外，SINDHWANI et al[13]使用再生核希尔伯特空间(RKHS)理论约束不同视图间一致性等。另一些方法通过挖掘视图间互补性信息来提升学习效果，如：MKMED模型[14]、鲁棒的多视图半监督学习方法(RMSL)[15]、多样化约束实现多视图的互补学习[16]等。2021年，新提出的CCA-based模型基于双反馈机制的多视图子空间学习模型(Multi-view subspace learning with dynamic double feedback mechanism，MSL-DDF)[17]是单视图增强表征和视图关系融合学习的新的多视图学习模式，模型在DGCCA模型基础上采用了动态路由机制学习单视图高阶特征，在分类和聚类任务的学习性能中均表现优越。

随着多视图数据结构、关系越来越复杂，特征越来越丰富，多视图学习的最终目标是要实现信息间相互补充[18-19]，在该过程中，不同视图蕴含独特信息的表征程度和互补融合方式决定了最终表征效果的质量[20]。基于该问题，为最大程度地利用多视图数据的有效信息，同时学习单视图独特特征和多视图互补性特征，本文提出一种基于深层特征增强的多视图隐空间融合表征方法(enhancing feature deep learning to improve multi-view latent space fusion representation，简写为MLSFR)，MLSFR由单视图增强学习、多视图互补融合、基于聚类任务导向的自表达学习三个子模块组成。在MLSFR模型中，多视图数据的计算主要有四个阶段：1) 挖掘单视图独特性特征，增强单视图的表达能力；2) 实现多视图的互补融合，学习多视图特征的共享隐表示矩阵，满足分类任务需求；3) 以聚类任务为导向，进一步学习融合表征的自表达矩阵。本文主要贡献为：1) 提出了一种同时探索单视图独特特征和多视图互补性特征的学习模型；2) 通过多目标设计，学习到满足于分类任务的隐空间表征和满足于聚类任务的自表达矩阵。

1 方法描述

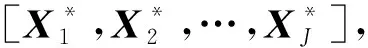
本文MLSFR模型如图1所示，主要过程为：第一步，单视图增强学习，包括：基于卷积操作提取视图的基础特征、利用多组卷积核构造特征图来丰富特征、特征向量化表示及动态路由学习；第二步，在单视图丰富表征后，进而进行多视图间的自监督表达，实现互补融合学习，得到视图的共享隐空间，并利用该隐空间进行分类任务；第三步，为使融合表征适用于聚类任务，在模型的末端加入以聚类任务为导向的自表达学习过程，利用包含单视图独特性和视图间互补性的隐空间作为该子模块的输入，基于自表达的子空间聚类算法，将隐空间H作为字典进行再学习，得到自表达矩阵Z，最后计算相似度矩阵S，进行聚类。

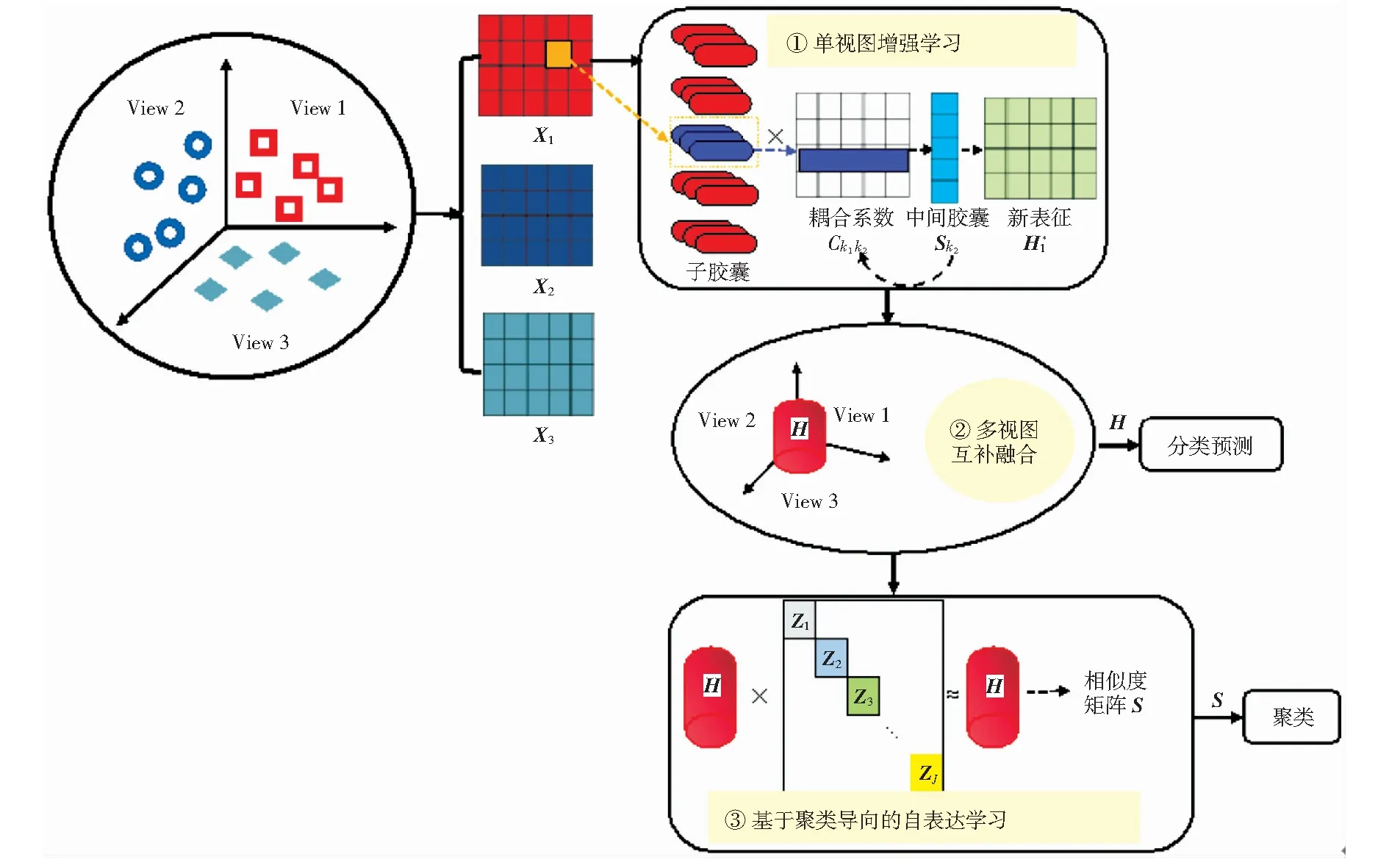
图1 MLSFR模型Fig.1 MLSFR Model

1.1 MLSFR算法描述

ZHANG et al[21]提出了一种多视图隐空间聚类学习模型(latent multi-view subspace clustering，LMSC)，该模型先学习多视图隐空间，再利用传统子空间聚类方法学习隐空间的自表达矩阵。受该模型启发，为提升LMSC中隐空间表示的分类预测性能和LMSC子空间聚类中自表达矩阵的聚类学习性能，本文加入了单视图特征增强学习。

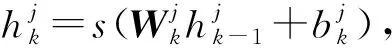
图2 单视图基础特征学习Fig.2 Basic representation learning of single view

本文算法包含三步。

1.1.1单视图特征增强学习

与深度网络不同，胶囊网络引入了“胶囊”概念，胶囊是由一组神经元组成的向量[22]，该向量模长表示实体对象中某部分特征存在概率，向量方向表示实体对象的各类属性，如：角度、位置、大小、颜色等。简言之，深度网络用标量形式的神经元只能表示实体存在的概率，胶囊网络采用向量形式的基本单元，不仅能表示实体存在的概率，还能表示该实体不同特征的相关属性。另外卷积神经网络采用最大池化操作提取高级别特征会丢失部分位置信息，胶囊网络采用动态路由算法，并使用转换矩阵实现部分和整体之间的内在空间关系的编码，更好地保留了实体与实体的空间位置信息。由于胶囊网络具有更强的表征学习能力，更符合人类神经系统的认知过程，更具解释性，成为了研究热点并应用广泛。因此，本文采用胶囊网络学习视图的深层特征并增强单视图特征的表达能力。

胶囊网络结构如图3所示。图中Step1与传统卷积神经网络的卷积运算一样，通过256个9×9的卷积核，得到20×20×256的特征矩阵。Step2和Step3为主胶囊层运算过程，该步骤操作与CNN有明显区别，采用8组卷积核生成8组特征图，丰富了特征，并将8组特征图展开成一维向量表示，得到1 152个胶囊向量，其作为动态路由算法的输入，实现了标量到向量的转化，而CNN在整个运算过程中一直是标量。Step4和Step 5为动态路由算法过程，图中激活向量的模长大小表示预测结果。

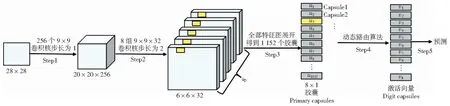
图3 胶囊网络结构Fig.3 Structure of capsule network

以第一个视图为例，假定视图特征O1按照上述操作分解成若干个胶囊，表示为：u1,…,uk1.动态路由算法过程描述如下：

(1)

(2)

式中：ck1k2是耦合系数，在动态路由算法过程，该系数通过softmax函数进行更新，表示上一层胶囊对于生成下一层各胶囊的贡献度。

上式中，耦合系数ck1k2的计算表达式为：

(3)

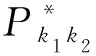
激活函数采用如下非线性函数：

(4)

(5)

1.1.2多视图互补融合

minP,HLh(X*,PH) .

(6)

其中，Lh(·,·)为损失函数。

隐空间学习过程如图4所示。该过程得到的隐空间H为多视图的融合表示，可直接用于完成分类任务。

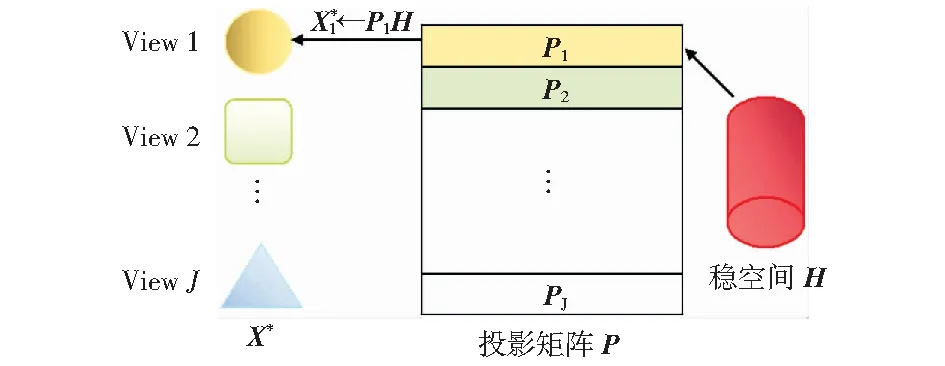
图4 隐空间学习Fig.4 Latent space learning

1.1.3基于聚类导向的自表达学习

上一步得到的融合表征H未基于聚类任务进行训练，因此，本文引入多视图子空间聚类模型，学习得到适用于聚类任务的融合表征矩阵。为清楚介绍该子模块，先简要介绍一下单视图子空间聚类方法：

假设样本数据集X=[x1,x2,…,xn]∈Rd×n包含n个样本向量，共j视图，xn的维度为d，单视图子空间聚类是将样本向量xa用该子空间中的其他样本向量线性组合表示为：

xa=xbZab.

(7)

当xa与xb不属于一类，即不在同一子空间，则特征向量xa的自表达矩阵Zab=0.若该样本有j类，则有j个自表达矩阵。自表达矩阵学习目标函数为：

(8)

其中，E为异常噪声数据，Z∈Rn×n，L(·，·)为损失函数，Ω(·)为正则化项，α>0为均衡因子，λ为权衡参数。最后，基于自表达矩阵构造相似度矩阵S进行聚类。

基于单视图子空间聚类算法，本文利用隐空间H学习适用于聚类任务的多视图自表达子空间，目标函数设计为：

(9)

其中，Z(j)为第j个视图的重构系数矩阵，L(·，·)为损失函数，Ω(·)为正则化项，其可以挖掘不同视图子空间的关系，λ>0为均衡因子。

构建模型总目标函数：

(10)

考虑到模型的鲁棒性，采用低秩表示的子空间学习方法，目标函数表示为：

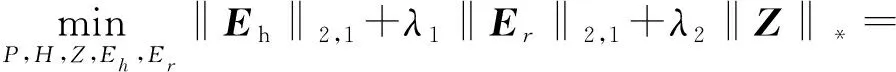
(11)

式中：Eh为隐空间重构误差矩阵，Er为隐空间H中的噪声数据矩阵，λ1、λ2为权衡参数，‖·‖2,1为矩阵的l2,1范数，满足矩阵的自反性非负性、对称性和三角不等式关系。

1.2 算法优化

考虑目标函数并非全部变量的凸函数，采用基于交替方向最小化的增广拉格朗日乘子法(augmented lagrange multiplier，ALM)求解矩阵秩最小化问题。首先，构造目标函数对应的增广拉格朗日函数：

L(P,H,Z,Eh,Er,M)=‖Eh‖2,1+λ1‖Er‖2,1+
λ2‖Z‖*+Φ(Q1,X-PH-Eh)+Φ(Q2,H-
HZ-Er)+Φ(Q3,M-Z)=‖E‖2,1+λ‖M‖*+
Φ(Q1,X-PH-Eh)+Φ(Q2,H-HZ-Er)+
Φ(Q2,M-Z) s.t.PPT=I,M=Z.

(12)

然后使用拉格朗日乘子法交替迭代矩P，H，Z，E，M，直到满足终止条件为止。将目标函数分解成单变量更新的子问题进行优化，分别更新P，H，Z，E，M及Q1，Q2，Q3的几个子目标，直到收敛。分别如下：

1) 更新投影矩阵P.固定除变量P以外的其他变量，得到关于变量P的优化函数为：

(13)

(14)

2) 更新隐空间矩阵H.固定除变量H以外的其他变量，得到关于变量H的优化函数为：

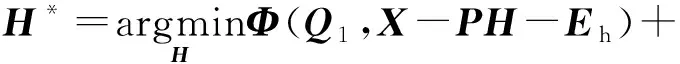
(15)

对H求导并使其0，求得：

A=μPTP.

(16)

B=μ(ZTZ-Z-ZT+I) .

(17)

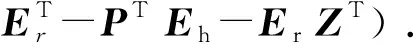
(18)

由此得到Sylvester方程求H的唯一解，其中，A为正定矩阵，B为半正定矩阵，且A和B间不存在共同的特征值。

3) 更新自表达矩阵Z.固定除变量Z以外的其他变量，优化函数表示为：

(19)

对变量Z求导令其为0，求得解为：

Z*=(HTH+I)-1[(M+HTH-HTEr)+
(Q3+HTQ2)/μ] .

(20)

4) 更新误差矩阵E.固定除变量E以外的其他变量，优化函数如下：

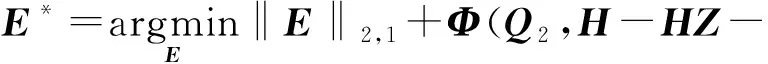
(21)

通过相关文献中的定理，变量Er和Eh的解分别为：

(22)

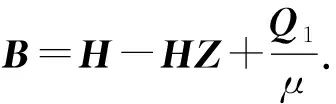
(23)

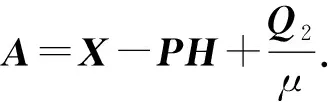
将A和B共同构成矩阵G，优化函数简化为：

(24)

5) 更新M.优化函数如下：

(25)

这里采用奇异值阈值方法求解M，对矩阵Z-Q3/μ进行奇异值分解，得到变量M解：

(26)

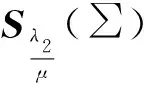
6) 更新拉格朗日乘子Q1，Q2，Q3.根据ALM算法，拉格朗日乘子的更新函数如下：

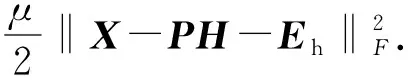
(27)

(28)

(29)

令其为0，求得解为：

Q1=Q1+μ(X-PH-Eh) .

(30)

Q2=Q2+μ(X-PH-Er) .

(31)

Q3=Q3+μ(M-Z) .

(32)

通过交替迭代上述每个变量，直到收敛。最后将包含视图差异性特征和一致性特征的隐空间矩阵H作为分类的输入，利用Z构建的相似矩阵P作为聚类的输入。

2 实验结果与分析

2.1 数据集

在以下多视图数据集进行实验。1) ORL.40个不同人的图像，包括三个特征：intensity，LBP，Gabor，三个特征看作3个视图。2) Football.为Twitter上20个俱乐部248名英超足球运动员信息，共9视图：followed by、follows、list-merged 500、lists500、mentioned by、mentions、re-tweeted by、re-tweets、and tweets500.其中，第1、2、5、6-8视图为关系网络，第9视图为文本，第3和4视图为IDs.3) Handwritten.为0-9数字的2 000张图片样本，共6视图，共包括6个特征，作为6个视图，分别为：Fourier coefficients of the character shapes，profile correlations，Karhunen-love coefficients，pixel averages in 2×3 window，Zernike moment，morphological.4) Wikipedia.维基百科文章，由2 866个图像/文本对组成，2 866个图像/文本对组成，每篇文章共图像、文本两个视图。

2.2 评测标准及基准算法

在分类任务中，采用精度(precision)、召回率(recall)、F1值和准确率(accuracy)，在聚类任务中，采用精度(precision)、召回率(recall)、F1值和准确率(accuracy)、轮廓系数(Silhouette_score)。与9种基准算法进行对比，具体如下：

1) LMSC.本文模型是基于该模型改进的[21]。该方法为多视图的子空间聚类，先计算隐空间，再利用学习到的自表达矩阵进行聚类，本文重点研究提升隐空间的能力，将LMSC模型学习的隐空间作为分类任务的输入矩阵得到分类预测结果与本文模型进行对比。

2) Co-Reg SPC.该算法采用协同正则化思想，实现多视图的一致性表达[23]。

3) LRRBestSV.该算法是最好的单视图子空间低秩聚类表征学习方法[24]。

4) Min-Disagreement。基于“最小化分歧”思想，创建二部图。解决两视图谱聚类的问题[25]。

5) RMSC.该算法将每个视图构造成一个转移概率矩阵，然后利用这些矩阵恢复出共享的低秩转移概率矩阵，作为聚类算法的输入，该方法具有低秩稀疏分解的特点。另外，为解决模型的优化问题，算法提出了基于增广拉格朗日乘子格式的优化方法[26]。

6) CCA.该算法计算两视图的最大相关系数，即两视图的相关性最大[2]。

7) DCCA.该算法是CCA基于深度网络的扩展，能够学习两视图的非线性映射，再计算最大相关系数，但有视图数量的局限性[6]。

8) DGCCA.该算法解决了DCCA和GCCA不足[7]。

9) MSL-DDF.该算法为CCA-based改进算法，优于最新DGCCA方法[17]。

具体地，实验结果分析中，根据算法适用任务不同，聚类任务中基准算法为：LMSC、Co-Reg SPC、LRRBestSV、Min-Disagreement、RMSC、CCA、DCCA、DGCCA、MSL-DDF；分类任务中基准算法为：LMSC、CCA、DCCA、DGCCA、MSL-DDF.

2.3 聚类任务结果与分析

本文方法是在LMSC基础上加入动态路由机制，因此，首先验证采用动态路由机制对提升LMSC隐空间学习效果的可行性，如图5所示，在3个数据集上聚类结果均提升，表明提高视图的表征能力可直接提升隐空间的学习能力，从中分析原因为：动态路由机制中采用向量形式表示单视图能够更好地表示实体不同特征的属性，并使用转换矩阵实现内在空间关系、实体与实体的空间位置信息学习，实现了更丰富、更具体的信息表达。实验中另加入轮廓系数指标，该指标值越接近1，说明聚类越合理，MLSFR在两数据集上轮廓系数均高于LMSC，表明加入动态路由机制可增强聚类性能。

图5 本文模型与LMSC模型的聚类性能对比Fig.5 Clustering performance comparison of our model and LMSC model

其次，利用单视图学习的隐空间的表征能力进行探索，结果如图6所示，从中发现：利用单视图分别学习隐空间，本文模型MLSFR性能总体不如LMSC模型，虽利用多视图学习后， MLSFR模型比LMSC模型学习效果更优，但MLSFR模型利用单视图学习能力较差。

图6 单视图融合表征的聚类性能对比Fig.6 Clustering performance comparison based on fusion representation of single view

然后，结合LMSC工作结果，与多视图聚类基准算法进行聚类性能分析，如图7所示，为Co-Reg SPC、LRRBestSV、RMSC、LMSC和本文模型较基准算法Min-Disagreement的F1提升率，可看出，本文模型较LRRBestSV的F1和Accuracy提升率分别为4.73%和19.25%，而LMSC模型较LRRBe-stSV的F1和Accuracy提升率为14.37%和11.56%，表明MLSFR的聚类准确性更高。

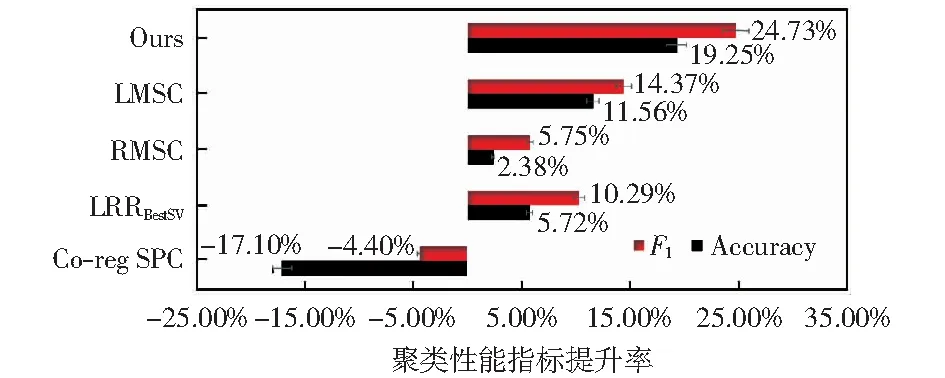
图7 MLSFR与多视图聚类算法性能对比Fig.7 Performance comparison of MLSFR and multi-view clustering algorithms

最后，探索了本文MLSFR算法与其他CCA-based方法的聚类性能差异性，结果如图8所示，从中看出：在Football数据集上，虽LMSC的F1性能最优，但MLSFR均高于CCA-based方法。在Handwritten数据集上，MLSFR的F1值高于LMSC，在Wikipedia数据集上，MLSFR低于CCA-based算法。结果证明：在视图数量越多的数据集上，本文聚类性能优势越明显。

图8 MLSFR与CCA-based方法的聚类性能对比Fig.8 Clustering performance comparison of MLSFR and CCA-based methods

综上分析，虽本文算法与基于子空间学习CCA-based方法相比，聚类性能提升并不突出，但本文算法较LMSC性能有明显提升，且较其他聚类方法的F1和准确率提升率明显，可见采用胶囊网络的动态路由机制挖掘视图深层增强特征可提升融合表征聚类性能，该研究有待继续深入。

2.4 分类任务结果与分析

采用90%的数据集作为训练集，10%的数据集作为测试集。隐空间H的维度设置为100，权衡参数λ选择从{0.001，0.01,0.1,10,100,1000}.

分类实验中采用Softmax分类器，隐空间矩阵维度为100.与聚类实验一样，首先，验证加入动态路由机制在分类任务中的提升效果，结果如表1，在ORL数据集上，MLSFR较LMSC的F1指标提高了1.2倍，在Football数据集上，MLSFR较LMSC的F1指标提高了8%，在Handwritten数据集上，MLSFR较LMSC的F1指标提高了21.3%，在Wikipedia数据集上，MLSFR较LMSC的F1指标提高了5%，结果表明MLSFR提升了多视图隐表征的分类性能。

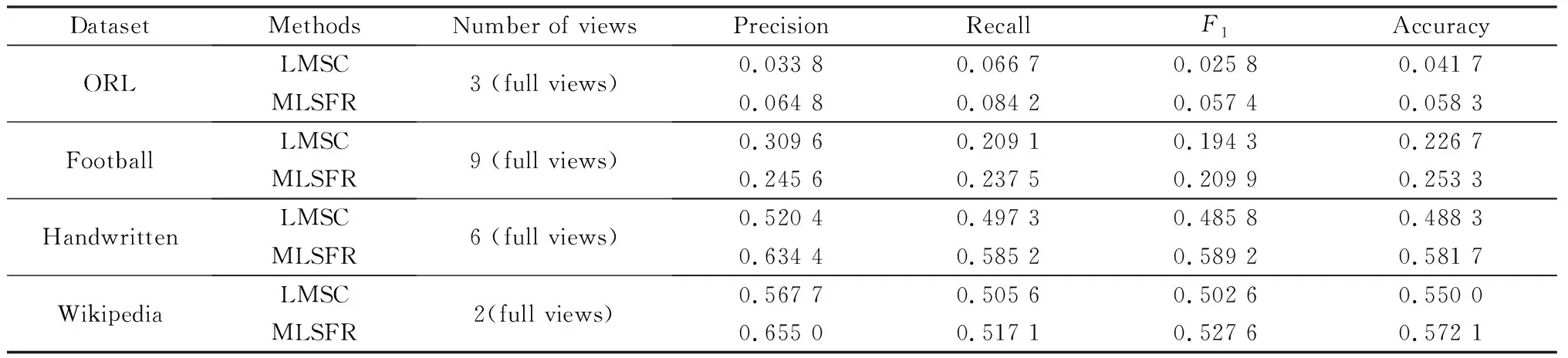
表1 MLSFR与LMSC的分类性能对比Table 1 Classification performance comparison of MLSFR and LMSC

然后，进一步对比单视图的隐空间学习性能，如图9所示，从中看出：MLSFR基本高于LMSC，证明模型提高隐空间表征的能力稳定。综上结果分析：本文模型在单视图分类性能差异较大时，融合表征后的分类能力下降。视图越多提高了融合表征计算复杂度高，影响融合表征聚类合理性。

图9 单视图融合表征的分类性能对比Fig.9 Classification performance comparison based on fusion representation of single view

另外，为验证本文模型在分类任务中的稳定性能，与其他CCA-based方法进行对比，结果如图10所示。从数据集分析，在视图较少数据集上，MLS-FR性能较稳定，在视图较多数据集上，性能不如CCA-based.从目标函数分析，CCA-based模型设计中以相关性最大为目标，而本文MLSFR只考虑到数据本身的全局相关性，未考虑局部关系，影响了模型的分类性能。

图10 本文模型与CCA-based模型的分类性能对比Fig.10 Classification performance comparison of our model and fusion representation models

3 结束语

本文为了丰富单视图特征的表达和实现多视图间互补学习，提出了一种基于多视图增强学习的隐空间学习方法，通过多目标设计，学习到满足于分类任务的隐空间表征和满足于聚类任务的自表达矩阵。为了增强单视图的独特性表达，对单视图提取基础特征、构造特征图丰富特征、特征向量化、动态路由学习。在单视图丰富表征后，进而进行多视图间的自监督表达，实现互补融合学习，得到视图的共享隐空间，并利用该隐空间进行分类任务。为了使得融合表征适用于聚类任务，在模型的末端加入以聚类任务为导向的自表达学习过程，利用包含单视图独特性和视图间互补性的隐空间作为该子模块的输入，基于自表达的子空间聚类算法，将隐空间H作为字典进行再学习，得到自表达矩阵Z，最后计算相似度矩阵S，并基于相似度矩阵进行聚类。最后在4个数据集上评测模型性能，表明：增强视图表征提升了模型聚类和分类性能；视图数量越多，聚类越好；模型聚类准确性高于基准算法；模型在单视图上分类差异较大时，融合表征后的整体分类下降。并发现模型在视图数量多时的聚类合理性略有下降，视图数量越多提高了计算融合表征的复杂度，影响了融合表征的聚类合理性，如何稳定地提升模型在大规模、视图数量多的数据集上的学习性能有待进一步研究。