电机静止主动发热能力分析

杨全凯，董继维，徐 斌

(浙江吉智新能源汽车科技有限公司,杭州 311228)

0 引 言

随着目前对电动汽车成本、重量、效率等指标要求越来越高，热泵技术由于其制热效率高而成为目前主要的研究方向之一。热泵通过制冷系统中制冷剂运行流向从车外空气吸热并向车内放热使得车内温度升高。但热泵系统在低温时由于空气中的热能有限导致制热性能降低[1]，此时需要发热元件(如PTC)介入提供额外的发热功率。但是增加单独的发热元件会增加整车成本及重量，另外一方面驱动电机在运行过程中产生的热量不能得到充分利用导致整车电耗增加。通过电机控制产生相应的发热功率用于整车热管理需求，不仅能够降低电动汽车成本、重量，还能够降低整车电耗，增加续航里程。因此，研究在控制电机转矩的同时调节电机效率进而控制电机发热功率具有重要意义。

目前电机控制研究方向主要为提高电机驱动效率[2-4]而对于在控制电机转矩的同时控制电机驱动效率进而控制发热功率方面的研究目前相对较少。由于电机采用效率最优控制方式时，电机产生的热量取决于电机的驱动转矩、转速及此工况点对应的效率，此时发热功率不可调节，存在发热功率无法满足整车热管理需求的情况，例如车辆冬天低温充电时需要对电池进行加热，而车辆此时静止且电机无转矩输出，因而此时电机无发热功率产生。由于整车热管理需求和驱动需求两者相互独立，驱动时需要电机提供相应的转矩，而热管理调节时需要电机提供相应的发热功率，所以需要通过电机控制实现电机转矩和电机效率的解耦控制。电机主动发热的功能为通过电机控制使得电机发热功率不依赖于电机运行工况，在控制电机转矩满足控制精度的前提下，根据发热功率需求主动调节电机运行效率进而调节电机发热功率的工作方式。特斯拉在专利(专利号：US13172786)中提到通过控制转子磁链使得异步驱动电机进入一种低效模式，使得电机产生更多的热量用于向动力电池加热，但专利中未公开具体电机控制方式。

由于按照效率最优的控制方法无法实现在车辆静止无转矩时响应热管理请求提供相应的发热功率，所以本文根据电动汽车电机主动发热功能需求，结合电机控制原理分析了在静止时实现电机主动发热功率的控制方式，按照此电机控制方式进一步分析电机允许最大电流限制的条件下电机最大发热功率能力与电机转子位置之间的关系，最后通过多组仿真及数据整理分析验证了理论分析结果。

1 电机静止时主动发热控制策略

dq坐标系下电机转矩公式[5]如下，

Te=Pn[ψfiq+(Ld-Lq)idiq]

(1)

式中，Te为电机电磁转矩，Pn为电机极对数，ψf为永磁体磁链，Ld为d轴电感，Lq为q轴电感，id为d轴电流，iq为q轴电流；

在电机静止时，控制目标为电机产生的输出转矩为零，且能够通过控制电机产生相应的发热功率。通过电机转矩公式可知，将q轴电流iq控制为零，根据目标发热功率控制d轴电流id，使得定子磁场与电机转子磁场平行，此时无转矩产生，电机三相绕组电流会产生相应的发热功率。根据标幺化之后的转矩公式绘制dq坐标系下的恒转矩曲线，可以看出iq=0横轴为零转矩曲线，静止发热时电流轨迹为d轴，根据目标发热功率电流轨迹在d轴上移动，距离原点越远电流越大，相应的发热功率越大。所以按照此控制策略可实现电机静止时对电机发热功率的控制。

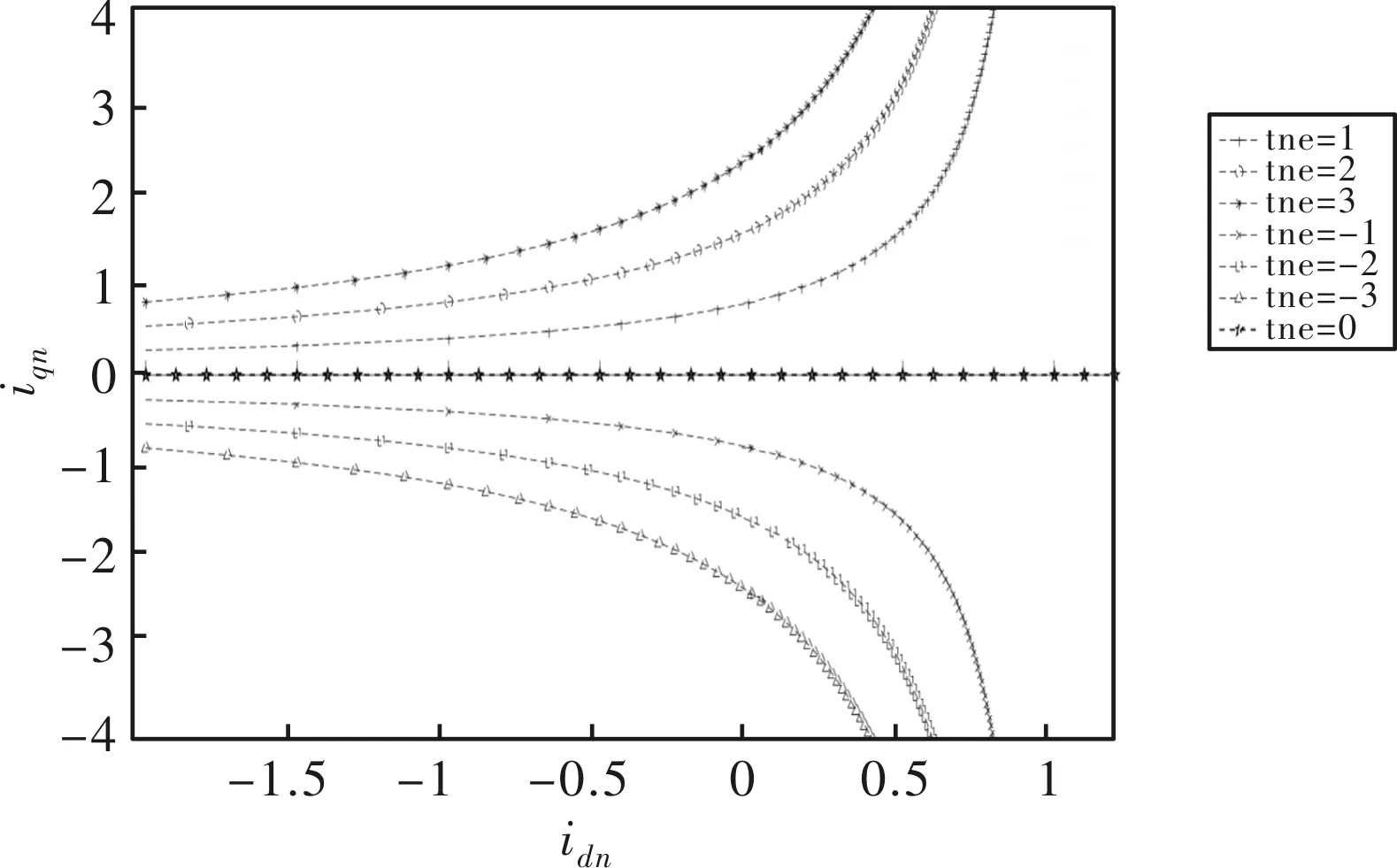
图1 标幺化后电机恒转矩曲线轨迹

电机损耗包括电机损耗和电机控制器损耗。电机损耗分为定子铜耗、定子铁耗、转子风摩损耗、转子涡流损耗、杂散损耗等。定子铜耗为定子电流在电机绕组上产生的损耗，包括直流电阻产生的损耗及趋肤效应产生的高频附加损耗。直流电阻产生的损耗与电流幅值及定子绕组直流电阻阻值有关，趋肤效应产生的高频附加损耗与电机工作频率、绕组导体、尺寸和在槽中的排列位置等多种因素有关。定子铁耗包括磁滞损耗、涡流损耗、异常涡流损耗，与铁芯材料和形状有关[6]。转子风摩损耗为转子表面与空气高速摩擦造成，与转速有关。机械杂散损耗包括机械摩擦损耗及谐波造成的损耗。电机控制器损耗包括导通损耗与开关损耗，导通损耗与导通电流及导通压降有关，开关损耗与开关频率、开关特性、电流等因素有关[7]。在静止时由于电机未处于旋转状态，电机的通入的电流为直流电流。根据电机损耗产生的基本原理，电机此时产生的损耗主要为定子铜耗，由于电机控制器损耗相对于电机损耗相对较小，所以本文中忽略不计电机控制器损耗。

2 电机静止主动发热功率能力分析

根据之前电机静止时主动发热原理分析可知，电机静止主动发热时定子三相绕组中的电流为直流，在忽略谐波损耗的情况下，电机产生的发热功率主要为定子铜耗。本文中分析静止电机发热功率能力时主要考虑电机定子铜耗，忽略谐波损耗和电机控制器损耗。由于电机绝缘等级及驱动系统输出电流能力等因素的影响，电机运行时的三相电流应不超过允许最大值。由于车辆停止时电机转子位置是随机的，而转子处于不同位置时电机最大发热功率能力及与转子位置之间的关系，目前未查到文献有相关研究。在三相电流不超过允许最大电流的情况下，电机静止发热功率的能力与电机转子位置之间的关系为本文分析的重点。

2.1 边界值分析法

受电机控制器驱动能力及电机绝缘等级等因素影响，电机运行时三相电流不允许超过其最大电流值Imax，即存在以下约束条件：

|IA|≤Imax,|IB|≤Imax,|IC|≤Imax

(2)

式中，IA为电机A相绕组电流；IB为电机B相绕组电流；IC为电机C相绕组电流；

根据基尔霍夫电流定律，电机三相电流矢量和为零，即：

IA+IB+IC=0

(3)

如前所述，在静止时电机三相定子绕组通入电流为直流电流，所以此时电机发热功率为三相定子绕组通入电流产生的铜耗，由于电机磁场静止，在忽略谐波损耗的情况下无铁耗产生。因而电机此时的发热功率为

(4)

式中，Ph为电机实际发热功率，Rs为电机定子绕组直流电阻阻值；

根据拉格朗日求取极值法，求取在式(3)条件下的式(4)的极值，构建拉格朗日函数为

求解得到在IA=IB=IC=0时取得极值，由于Ph≥0，此时Ph取得极小值。

根据式(3)可得

IC=-(IA+IB)

(5)

将式(5)代入式(2)和式(4)可得：

|IA|≤Imax,|IB|≤Imax,|IA+IB|≤Imax

(6)

(7)

所以最大发热功率为在满足式(6)的限制条件下求取式(7)的最大值。对式(8)进行一阶微分求取极值点：

(8)

综合以上二式求取极值点IA=0,IB=0;

对式(8)进行二阶微分，可得：

(9)

根据二元函数求取极值方法，在IA=0，IB=0时A=4，B=2，C=4，AC-B2>0且A>0。所以在IA=0，IB=0时Ph取得极小值，且只存在一个极值点。所以Ph的最大值应在IA、IB的边界上。

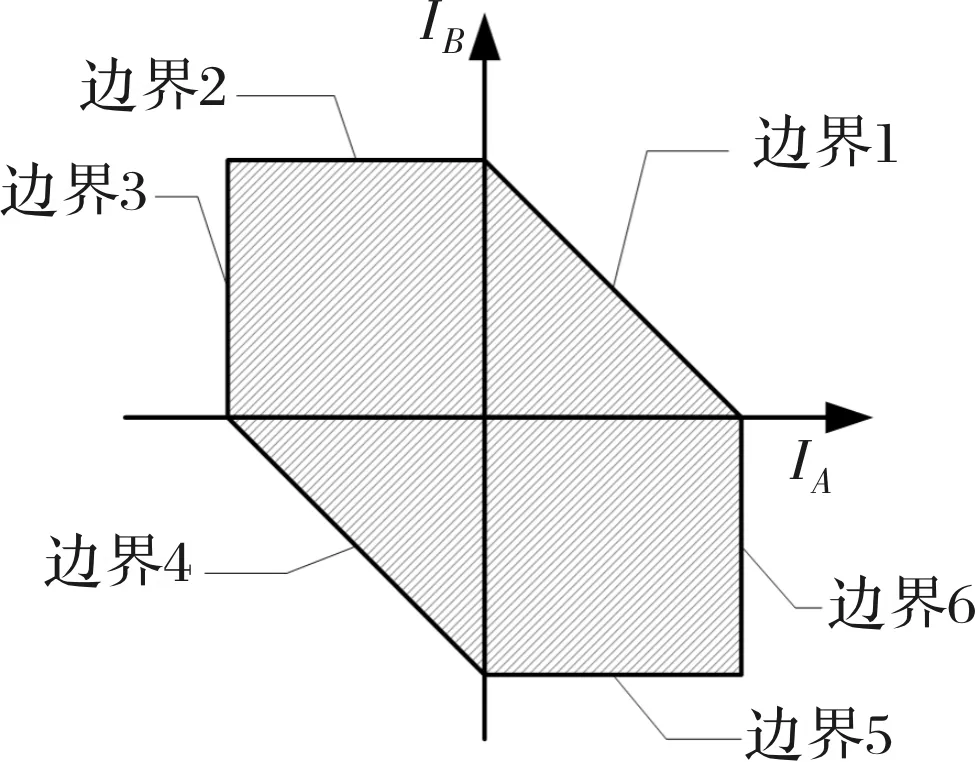
图2 IA,IB边界分布

边界1为：IB=-IA+Imax,IA∈[0,Imax];

边界2为：IB=Imax,IA∈[-Imax,0];

边界3为：IA=-Imax,IB∈[0,Imax];

边界4为：IB=-IA-Imax,IA∈[-Imax,0];

边界5为：IB=-Imax,IA∈[0,Imax];

边界6为：IA=Imax,IB∈[-Imax,0];

对以上边界值根据式(4)可以求得。

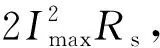
表1 边界值下发热功率最大值与最小值

边界值分析法能够分析出电机静止时主动发热能力的最大值及最小值及达到最大值或最小值的条件，但没有分析出电机静止时主动发热能力与转子位置之间的关系。下面在dq坐标系下分析电机静止时主动发热能力与转子位置之间的关系。

2.2 dq坐标系电机模型分析法

电机静止时通过控制d轴产生相应直流电流，控制q轴电流为零，将ABC坐标系向dq坐标系变换。

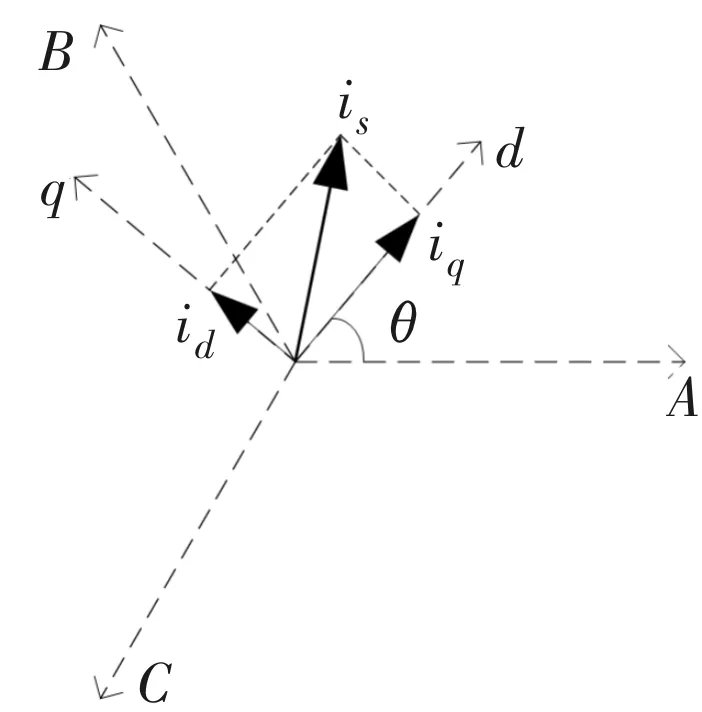
图3 ABC坐标系与dq坐标系变换

ABC坐标系与dq坐标系下的变换为

(10)

式中，θ为电机转子位置对应的电角度，Id，Iq为dq坐标系下的d轴电流与q轴电流。

根据电机在静止时的控制策略可知Iq=0，因此可将上式写为

(11)

可得

(12)

将式(12)代入式(4)可得电机发热功率Ph为

(13)

从式(13)可以看出，在Id一定的情况下，电机静止时的发热功率与电机转子位置无关。

但由于电机的三相电流不能超过允许最大值Imax，即

(14)

将式(12)代入式(14)可得

(15)

由式(15)可知，Id需要同时满足以上三项，所以可将上式转化为

(16)

设函数：

(17)

将式(17)代入式(16)可得：

(18)

电机发热能力为其能够达到的最大值，结合式(13)和式(18)可得：

(19)

(20)

根据式(12)可得：

(21)

式(21)周期为6，所以按照k=0，1，2，3，4，5情况分析，结果如下表。

从表2可以看出，主动发热能力最小时，三相电流其中一相为最大值，另外两相为最大值一半且方向与最大值向电流方向相反，与基于边界值分析时的结论一致。

表2 主动发热能力最小时k取不同值时三相电流

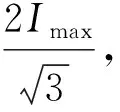
根据式(12)可得，

(22)

式(22)周期为6，所以按照k=0，1，2，3，4，5情况分析，结果如表3所示。

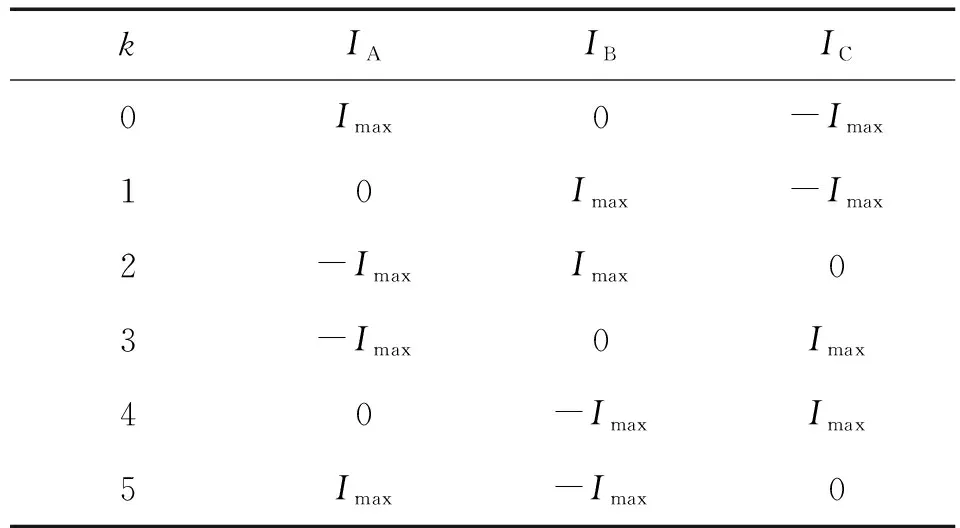
表3 主动发热能力最大时k取不同值时三相电流

从上表可以看出，主动发热能力最大时，三相电流其中两相为最大值，方向相反，另外一相电流为零，与基于边界值分析时的结论一致。

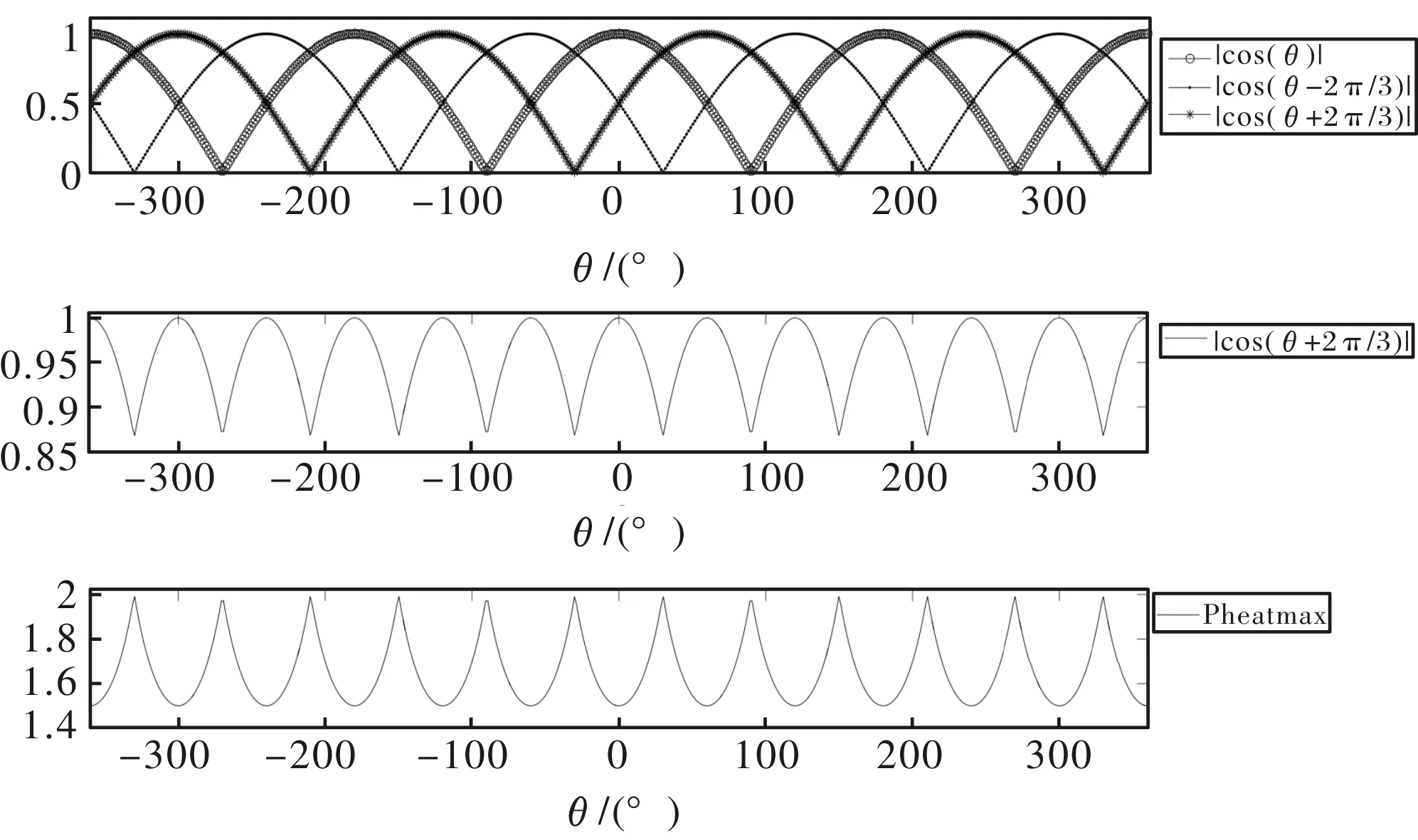
图4 电机静止主动发热能力与转子位置关系曲线

3 仿真验证

按照电机静止时主动发热控制策略，对不同位置时电机主动发热能力进行仿真验证。目标发热功率从零开始逐渐增加，并实时采集电机三相电流，取三相电流中最大值，如果三相电流中最大值达到允许电流Imax，则停止增加发热功率，此时的产生的发热功率为在此角度下允许电流时的电机发热能力。发热功率控制器通过将目标发热功率与实际发热功率进行比较调节d轴电流。如之前分析，电机静止时的发热功率主要为定子铜耗，所以本模型中实际发热功率根据三相电流幅值计算三相定子铜耗之和。

本仿真中，电机参数为定子电阻Rs：6e-3Ω，d轴电感Ld：100e-6H，q轴电感Lq：240e-6H，电机极对数Pn：4，永磁体磁链ψf：0.04 Wb，最大允许相电流Imax：400 A。

首先对电机转子位置为0°工况进行仿真。从图6及图7可以看出，随着发热功率逐渐增加，d轴电流逐渐增大，q轴电流保持为零，dq轴电流轨迹为随着发热功率增大沿着d轴逐渐左移，与之前分析一致。

从图8目标发热功率与实际发热功率曲线可以看出，实际发热功率能够跟随目标发热功率。图8中，将直流侧输入功率与电机轴端输出机械功率差值计算得到的发热功率与基于定子电阻计算的定子铜耗相比，两者曲线基本重合，说明电机静止主动发热时电机系统发热功率损耗主要为定子铜耗，与之前分析一致。从图8电机转矩曲线，电机的目标转矩与实际转矩均为零。从图8定子电流可以看出，随着发热功率目标值的增大，电机定子电流逐渐增大，其中A相电流为最大值达到400 A，B相、C相电流分别为200 A且电流方向与A相电流方向相反，与之前分析结果一致。

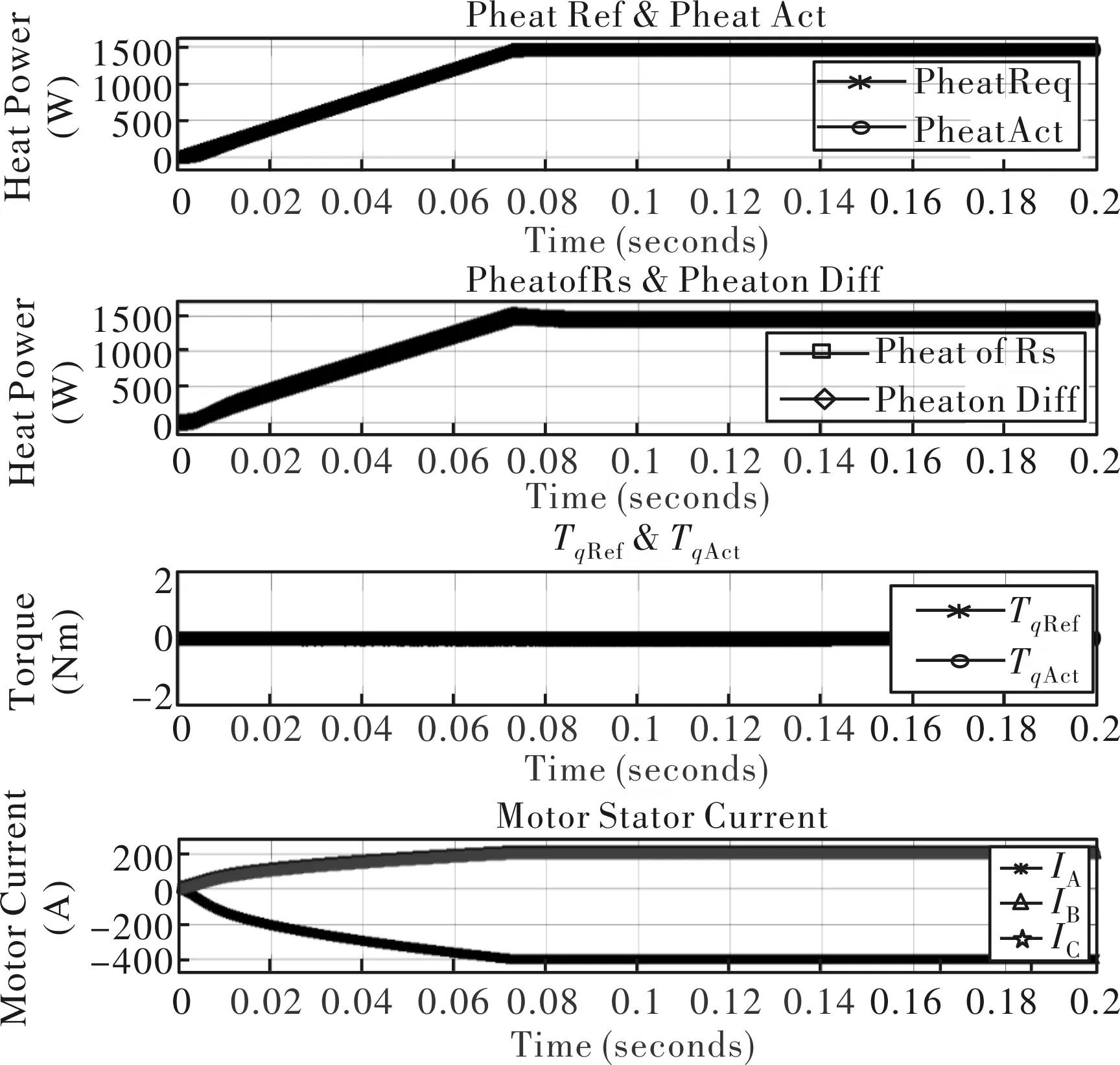
图8 静止发热时目标发热功率、基于定子铜耗的发热功率、基于输入输出功率差值的发热功率、电机转矩、电机三相电流曲线图

为了验证电机在静止时主动发热在允许电流范围内不同转子位置的发热能力，按照2°步长从0°至360°电角度进行多组仿真计算，得到不同位置下对应的电机发热能力。仿真控制流程图如图9所示。

图9 静止时在允许电流范围内电机转子不同位置主动发热能力仿真控制流程图

仿真结果如图10所示，从图中可以看出在转子位置电角度为0°时，电机主动发热能力最小为1457 W，在转子位置电角度为30°时，电机主动发热能力最大为1934 W，电机主动发热能力最大值与最小值比值为1934∶1457=3.98∶3，与之前理论分析比值为4∶3基本一致。将图10曲线与图4曲线对比，可以发现两者曲线的趋势及比例关系一致。

图10 在最大允许电流下不同转子位置下对应的电机主动发热能力曲线图

为了验证在Id电流一定的情况下，不同转子位置时的实际发热功率，按照2°步长从0°至360°电角度进行多组仿真计算。仿真控制流程图如图11所示。

图11 静止时d轴电流一定、电机转子不同位置时的电机实际发热功率仿真控制流程图

d轴电流目标值为-285.7 A，仿真结果如图12所示。从仿真结果可以看出，在d轴电流固定时，电机在不同转子位置时的实际发热功率为固定值，实际发热功率为746 W左右。仿真结果与式(13)结论一致。

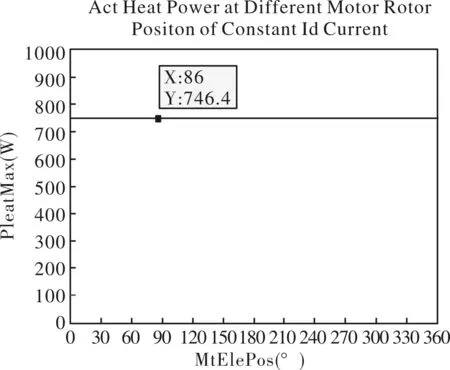
图12 d轴电流值固定时，不同转子位置下实际发热功率

4 结 语

(1)在电机静止且不允许输出转矩时，通过控制q轴电流为零，根据目标发热功率调节d轴电流能实现调节电机发热功率，进而实现电机静止时的主动发热功能。

(4)电机发热功率能力与转子位置的关系一方面可用于根据电机转子位置对应的电机发热能力调整电机目标发热功率进而获取最大的电机发热功率，另外一方面可用于明确在测试电机静止发热功率时对电机转子位置的要求。在不超过允许电流的情况下，电机发热功率只与d轴电流有关，根据此结论在不超过允许电流范围的情况下只需要计算或标定不同发热功率下的d轴电流，而不需要考虑电机的转子位置。

本文主要分析了电机在静止时的电机主动发热控制方案及发热功率能力与转子位置之间的关系，对于电机旋转之后实现电机转矩控制与发热功率控制的解耦控制还有待后续进一步研究。