考虑加工误差的表贴式永磁伺服电机齿槽转矩分析与抑制

姜 涛，曲诗健，孙佳伟

(中车大连电力牵引研发中心有限公司，辽宁 大连 116052)

0 引 言

近年来，随着稀土永磁材料的发展，永磁电机应用越来越广泛。永磁电机具有高转矩密度、高效率、高功率因数等优点[1]，满足了现代高性能伺服系统对宽调速范围、低速大转矩、稳定性好与快速动态响应的要求。但齿槽转矩是导致永磁电机转矩脉动的主要原因之一[2]，影响伺服电机控制精度，所以永磁伺服电机齿槽转矩的抑制尤为重要。

齿槽转矩是永磁体与定子齿之间相互吸引产生的[3]。现有文献提出了各种各样齿槽转矩抑制方法，但绝大多数是以理想模型为基础的理论分析与仿真计算，并未计及批量生产中可能存在的加工误差。包括定子参数优化的定子斜槽、不等槽口宽、定子齿开虚槽等方法，转子参数优化的优化极靴深度、转子斜极、优化极弧系数、磁极分段移位、磁极采用不对称角度、采用不等极弧系数等方法[4-11]，都是基于理想模型的。

计及加工误差后，齿槽转矩为两部分的叠加，第一部分为理想模型的齿槽转矩TNHC(Native Harmonic Components, NHC),另一部分为加工误差产生的额外齿槽转矩TAHC(Additional Harmonic Components, AHC)[12]，TAHC的产生导致文献[4-11]中的齿槽转矩抑制方法理论与实际区别较大。文献[13]定义了一个与槽数和极数有关的参数F，用来衡量TAHC对加工误差的敏感度。文献[14-15]研究了相同极性永磁体沿同一方向位移误差、单个定子齿误差和单个槽口宽误差对齿槽转矩的影响规律，但是没有考虑加工误差的随机性。文献[16]为了加快有限元的计算速度，将N极和S极永磁体(Permanent Magnet，PM)分别取相邻的一半作为一个单元，并对只考虑这个单元永磁体的电机进行有限元仿真，将齿槽转矩计算结果进行位移叠加得到最终的齿槽转矩，但只能针对理想模型。文献[17]从泊松方程和拉普拉斯方程出发，推导考虑加工误差的齿槽转矩解析模型，模型计算结果与有限元算法接近，但计算推导过程较为复杂。然而，以上文献均未分析齿槽转矩对各加工误差的敏感性以及加工误差对齿槽转矩概率分布的影响。

本文首先采用能量法建立解析模型，分别计算单一加工误差对齿槽转矩频谱的影响规律，以此判断对齿槽转矩影响最大的误差种类，指出了齿槽转矩实际与理论差距大的本质原因。再基于蒙特卡罗方法，结合有限元仿真软件，计算同时考虑所有加工误差后的齿槽转矩概率密度分布，以此预测量产电机齿槽转矩合格率。并且采用定子冲片循环旋转方法较好地抑制了定子侧误差产生的TAHC，同时进行了理论论证，得到了冲片依次旋转一个槽时齿槽转矩抑制效果最好的结论。最后，用实验验证了本文齿槽转矩分析抑制方法的可行性。

1 能量法模型

1.1 理想模型

根据能量法，齿槽转矩等于电枢绕组不通电时，永磁电机内部能量对定转子相对位置角的负导数。忽略定转子铁心中的能量，只考虑气隙和永磁体中的能量[18]，齿槽转矩为

(1)

(2)

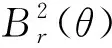
如图1所示，假定θ=0位置为指定的两个永磁体中心线，α为某一指定的定子槽中心线和θ=0位置所夹角度，即定转子相对位置角。

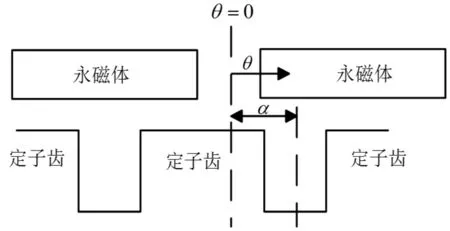
图1 永磁体与电枢相对位置

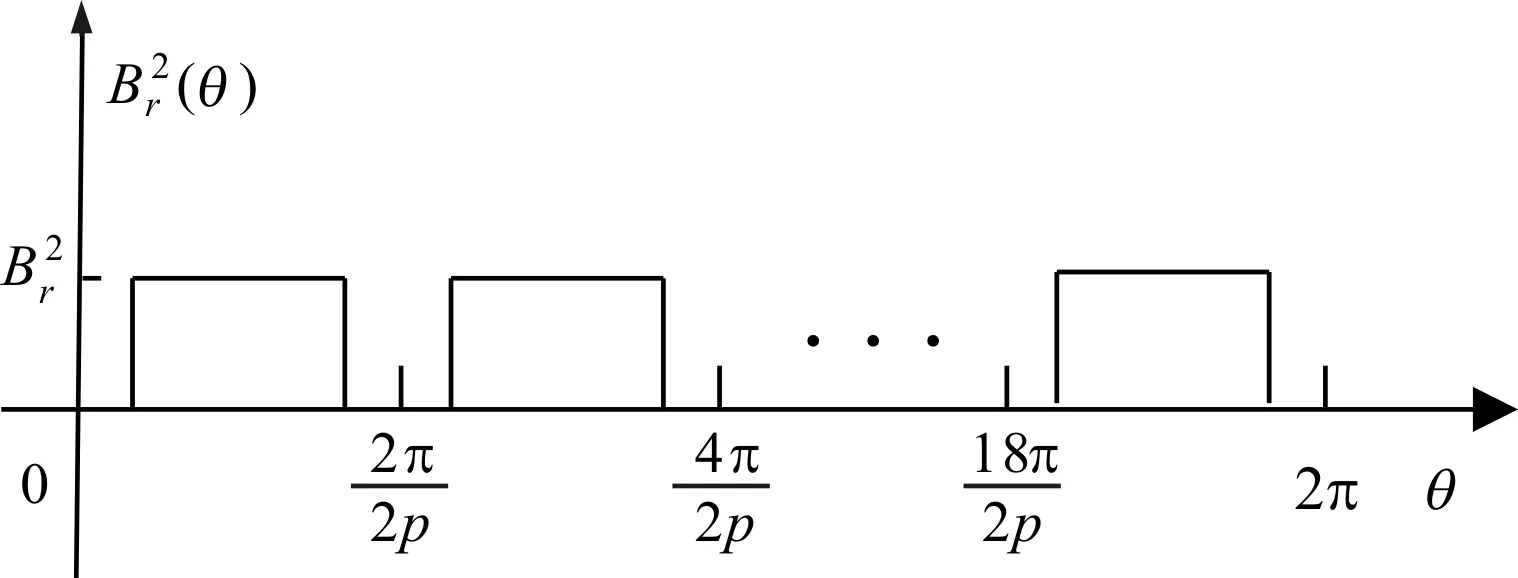
图2 的分布

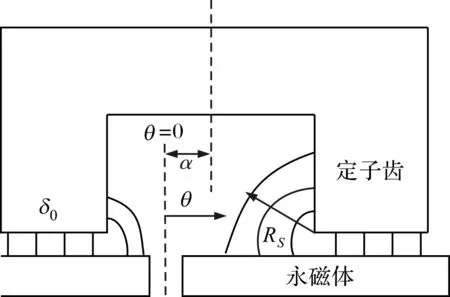
图3 定子槽中磁力线路径

永磁体对着定子槽的位置，假定槽中磁力线以四分之一圆弧路径进入定子齿，圆弧半径Rs等于磁力线进入位置到定子齿顶点的距离，气隙长度δ等于物理气隙δ0加上以Rs为半径的四分之一圆弧长度[19]。电机齿槽分布均匀，G2(θ,α)在周向上的分布如图4所示，So为槽口宽对应的机械角度。将式(4)带入式(2)，可得G2(θ,α)傅里叶展开如式:

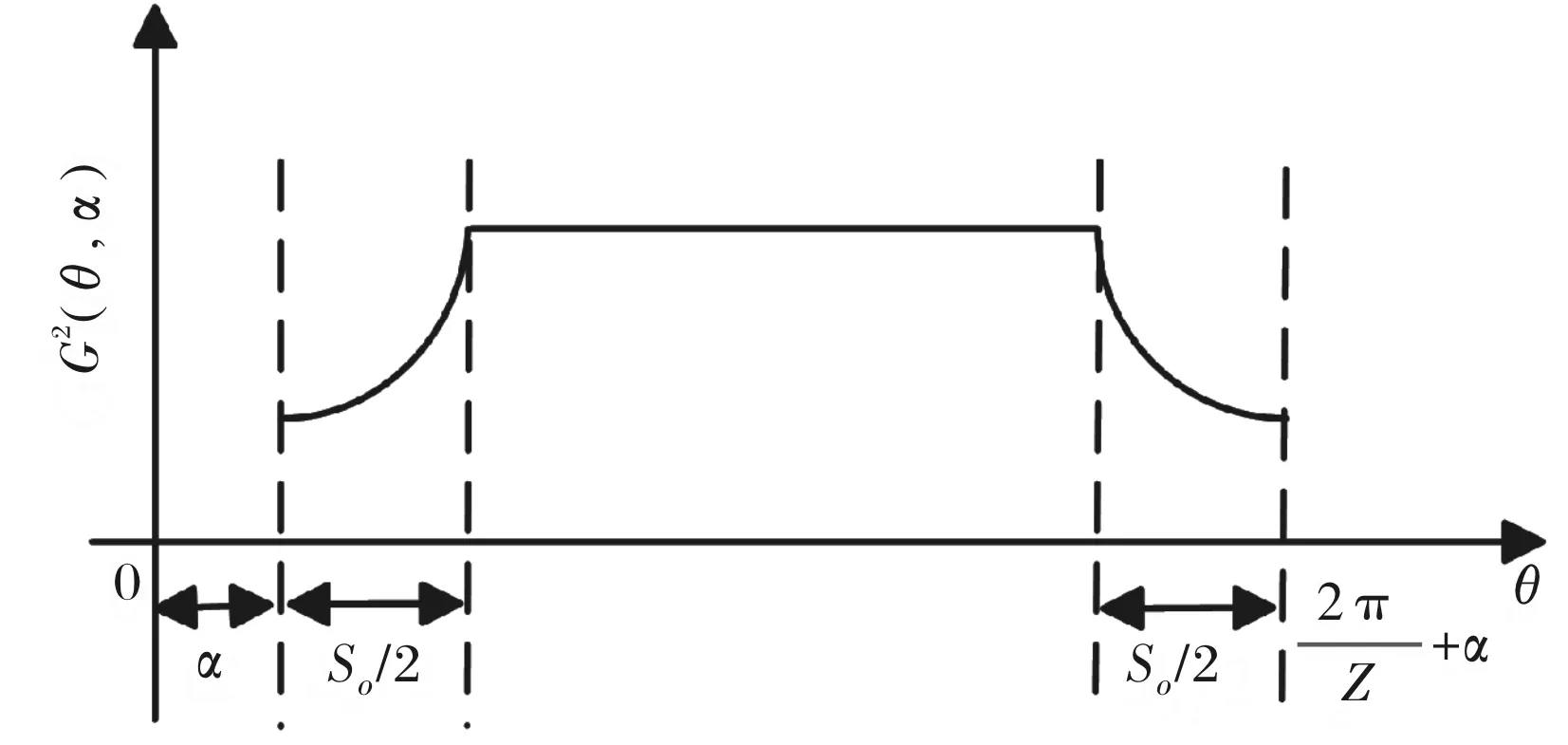
图4 G2(q,α)的分布

(3)

(4)

(5)

将式(3)、式(5)带入式(1)可得：

(6)

式中，La为电机铁心轴向长度，R1和R2分别为转子外半径和定子内半径，z为槽数，p为极对数，q为使得qz/(2p)为整数的整数

1.2 非理想模型

电机批量生产中，即使微小的误差，也可能造成齿槽转矩成倍增长。后文采用定子冲片循环旋转方法，能较好地抑制定子侧误差对TAHC的影响，故此处仅分析转子侧永磁体充磁、厚度、宽度、周向位置等误差对齿槽转矩的影响。

(7)

(8)

(9)

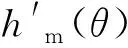
(10)

式中,m=n=q′z，q′为正整数。相比于式(6)新增了槽数倍数次齿槽转矩谐波。

1.3 加工误差敏感性分析

假定每块永磁体都各不相同，对于12槽10极电机来说，每块永磁体都将产生12次齿槽转矩谐波。基于12次谐波和相邻永磁体机械角度(36°)可以得到永磁体误差导致的额外齿槽转矩矢量图[19]，如图5所示。相邻两块永磁体产生的12次齿槽转矩谐波相位依次相差72°。根据该矢量图与表5所列加工误差的分布，可以直接得到各类误差对齿槽转矩影响最恶劣的情况并列于表1中。

图5 齿槽转矩矢量图

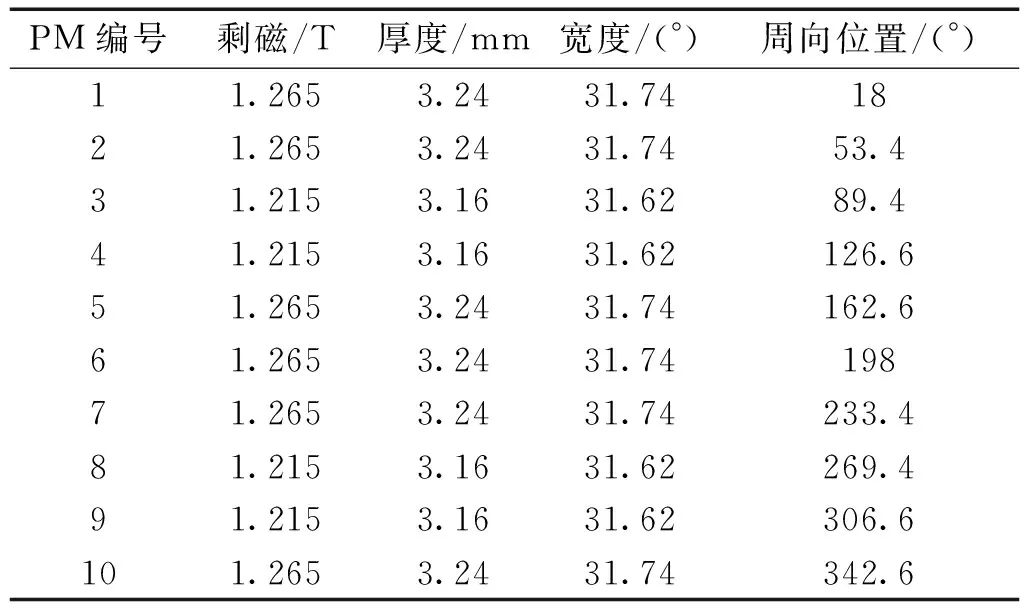
表1 计算模型永磁体参数

分别考虑永磁体4种误差，并结合表2中的电机标称参数，代入能量法模型，算得各次谐波幅值如图6所示。永磁体各种加工误差都将引入槽数倍数次的齿槽转矩谐波，并且对齿槽转矩影响最大的误差为永磁体周向位置误差。即永磁体周向位置是导致齿槽转矩理论与实际相差大的首要原因。因此，加强对永磁体周向位置加工精度，将产生较好的齿槽转矩抑制效果。

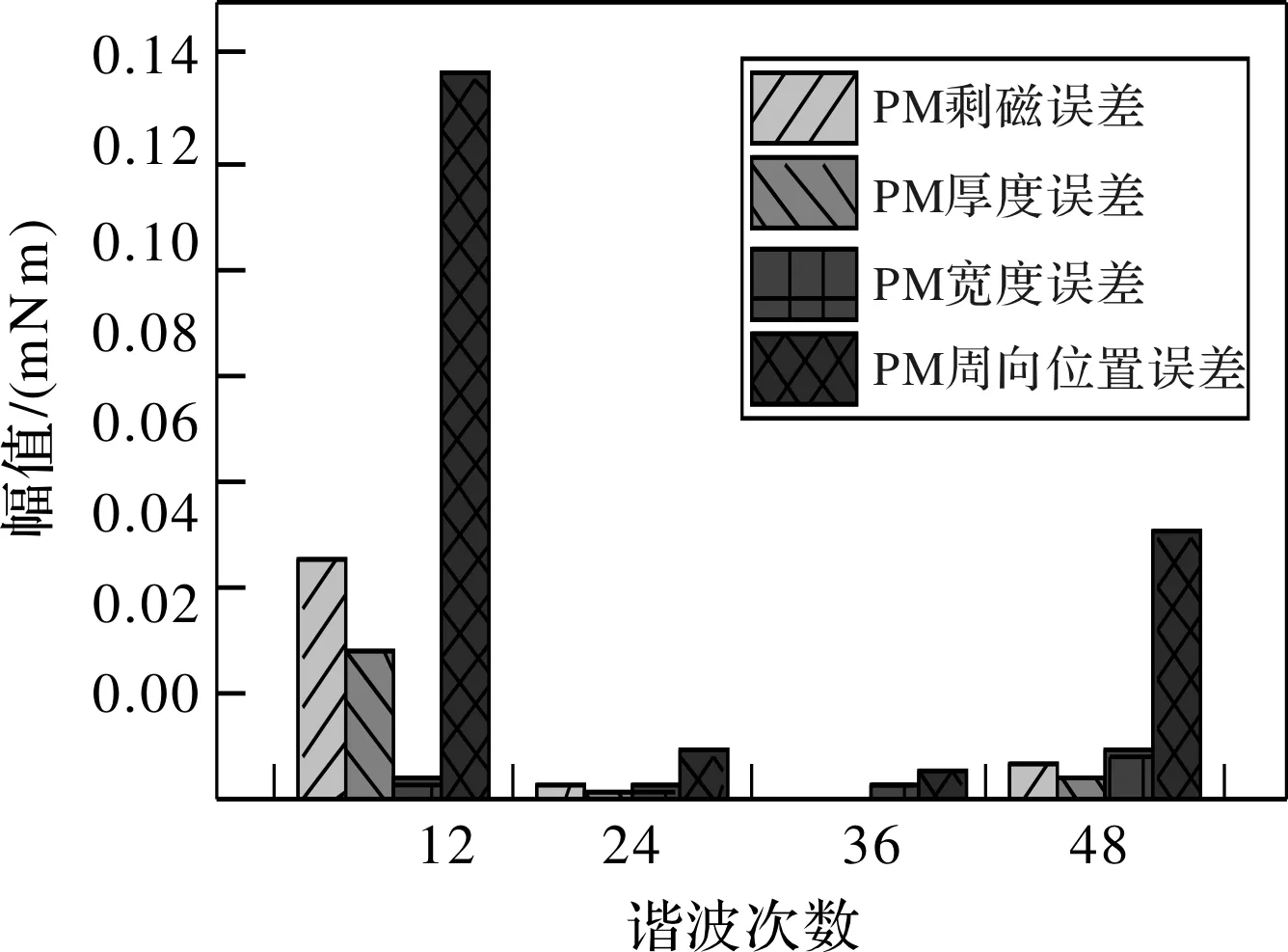
图6 各次齿槽转矩谐波幅值

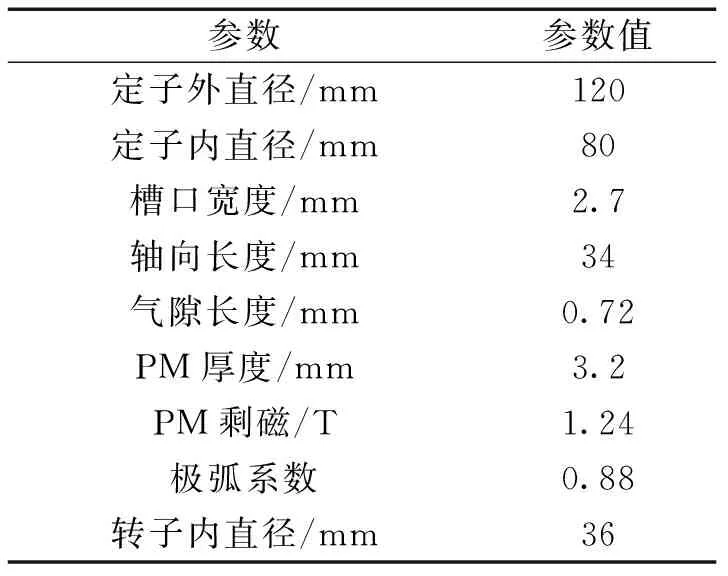
表2 电机标称参数

2 有限元模型

2.1 理想模型

本文针对一个12槽10极的表贴式永磁伺服电机进行研究分析，电机标称参数列在表2中，拓扑结构如图7所示。有限元计算的理想模型齿槽转矩波形及频谱如图8所示。在转子转动的360°机械角度内，齿槽转矩周期性变化，变化周期数为槽数与极数的最小公倍数[15]。

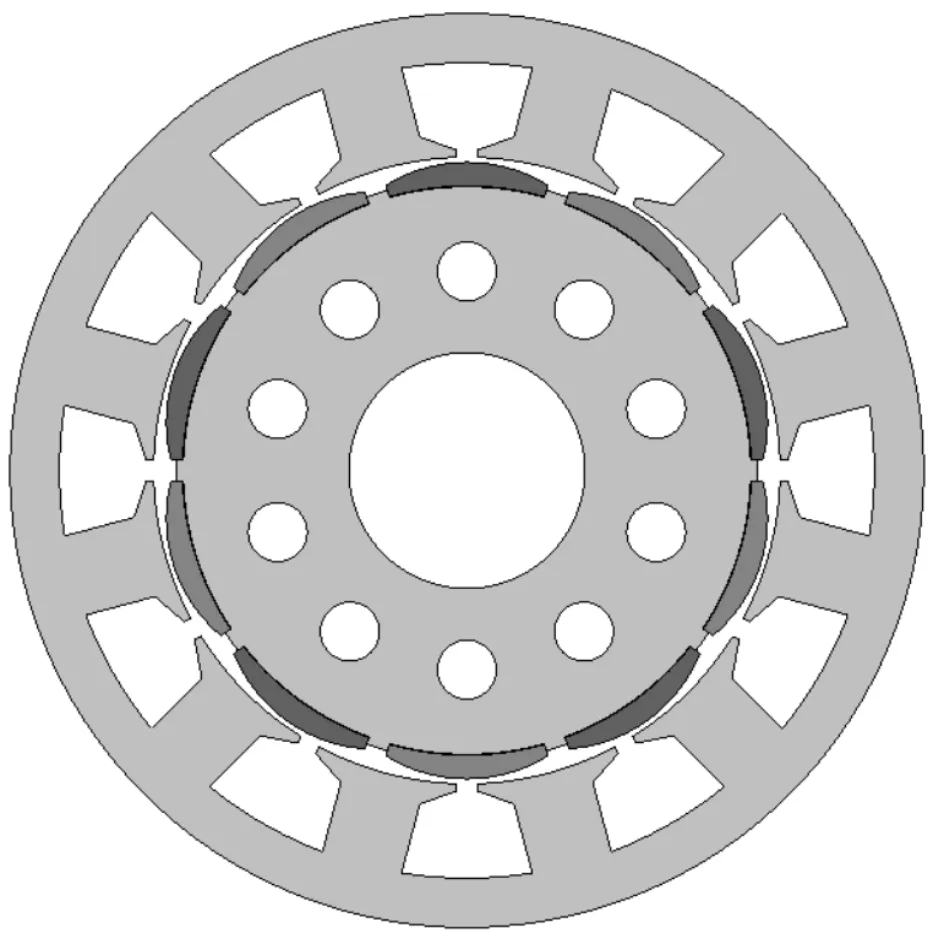
图7 电机拓扑结构

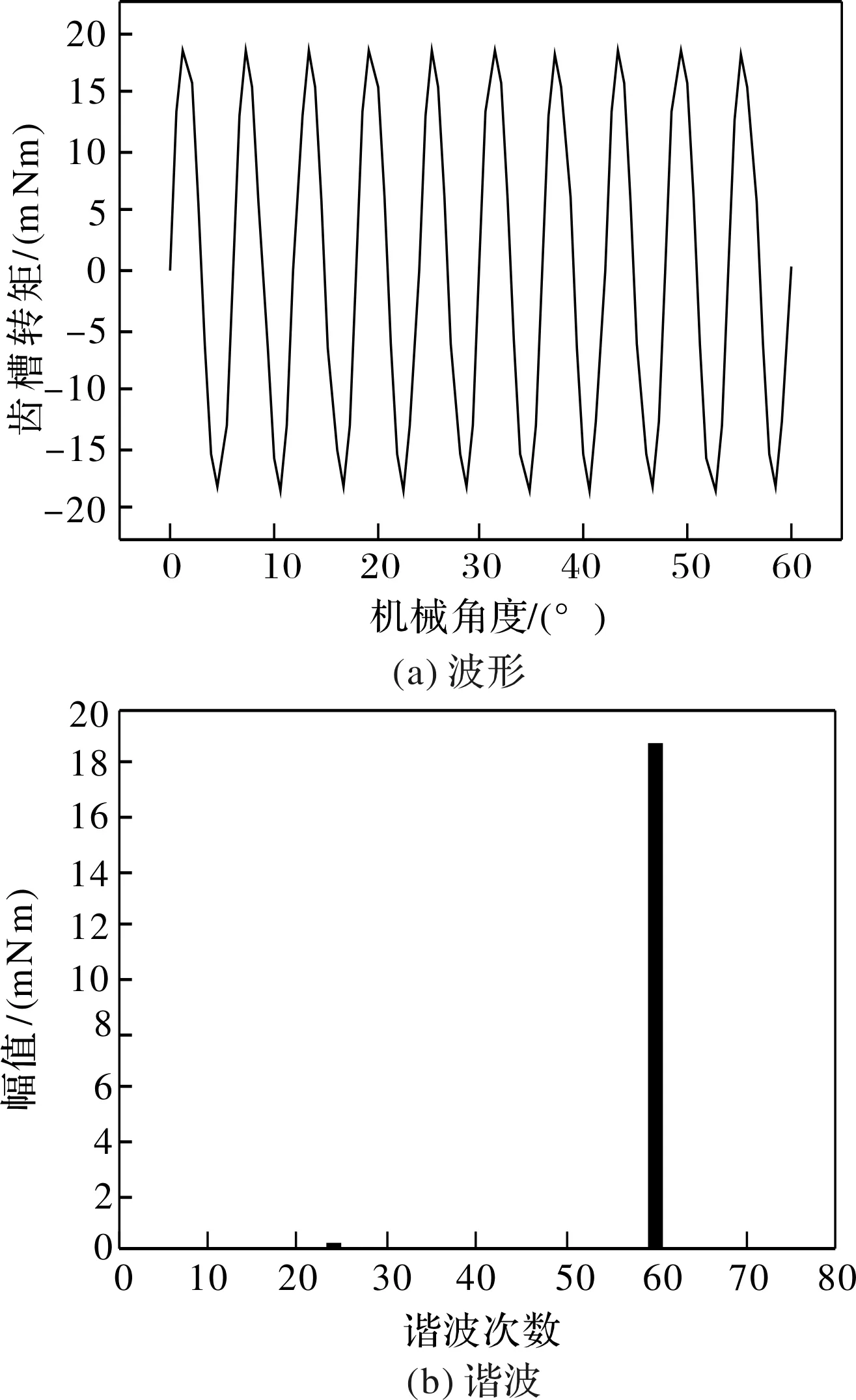
图8 理想模型齿槽转矩

2.2 齿槽转矩概率分布

如果随机变量X服从一个以μ为数学期望、σ2为方差的正态分布，即N(μ，σ2)。那么X落在区间(μ-3σ，μ+3σ)以外的概率小于千分之三，基本上可以把区间(μ-3σ，μ+3σ)看作是随机变量X实际可能的取值区间，这称为正态分布的“3σ”原则。

假定实际加工中电机各参数都服从正态分布，数学期望为对应参数标称值，方差通过对样机各参数测量得到。对一台样机的定子齿直径、PM宽度、PM厚度、PM表面磁密等参数进行测量，测量结果分别如表3、表4所示，其中，定子齿直径定义为两个相对定子齿的距离。

表3 定子齿直径误差

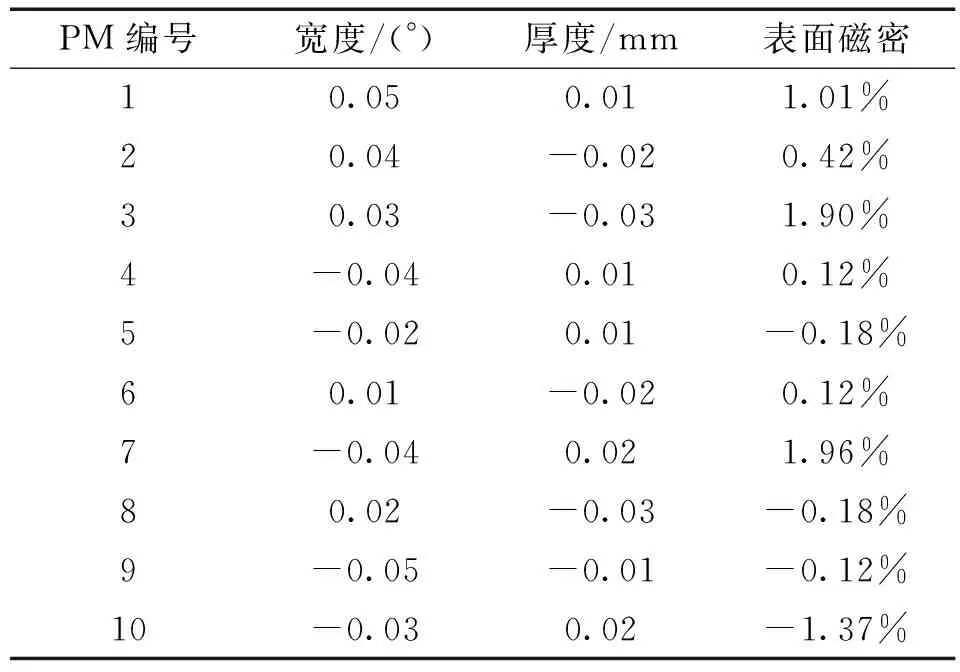
表4 永磁体误差

根据正态分布的“3σ”原则，各参数的标准差σ应等于相应最大误差的三分之一。但考虑到本次测量只是针对一个样机，样本数量有限，各参数的标准差取得稍大。定子齿直径最大误差为0.04 mm，建立有限元模型时，参数化定子齿半径，取其标准差为0.025/3 mm；PM宽度最大误差为0.05°，取标准差0.060°/3；PM厚度的最大误差为0.03 mm，取标准差0.040/3 mm；PM表面磁密最大误差为1.96%，取剩磁标准差为0.025/3T。

另外，有限元软件建模时，参数化定子槽口宽的一半，如图9所示，这样能同时考虑槽口宽度与位置误差。且PM周向位置与槽口宽误差由供应商提供，取PM周向位置标准差为0.600°/3，取半个槽口宽标准差为0.009/3 mm。具体参数列在表5中。

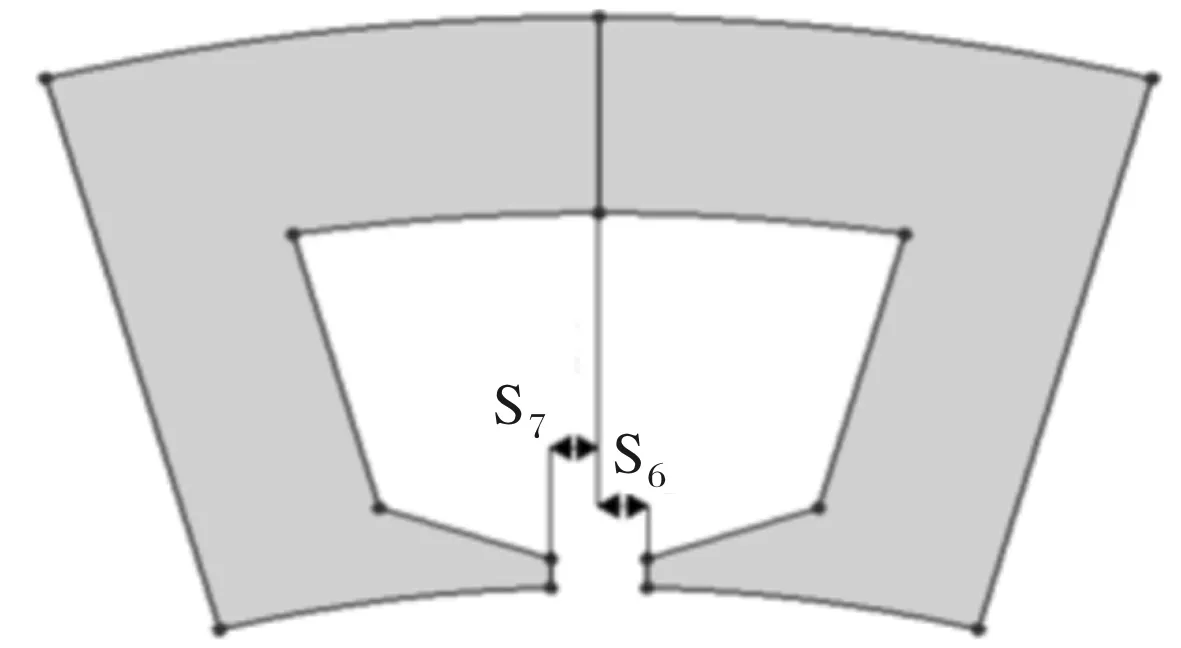
图9 槽口宽的一半

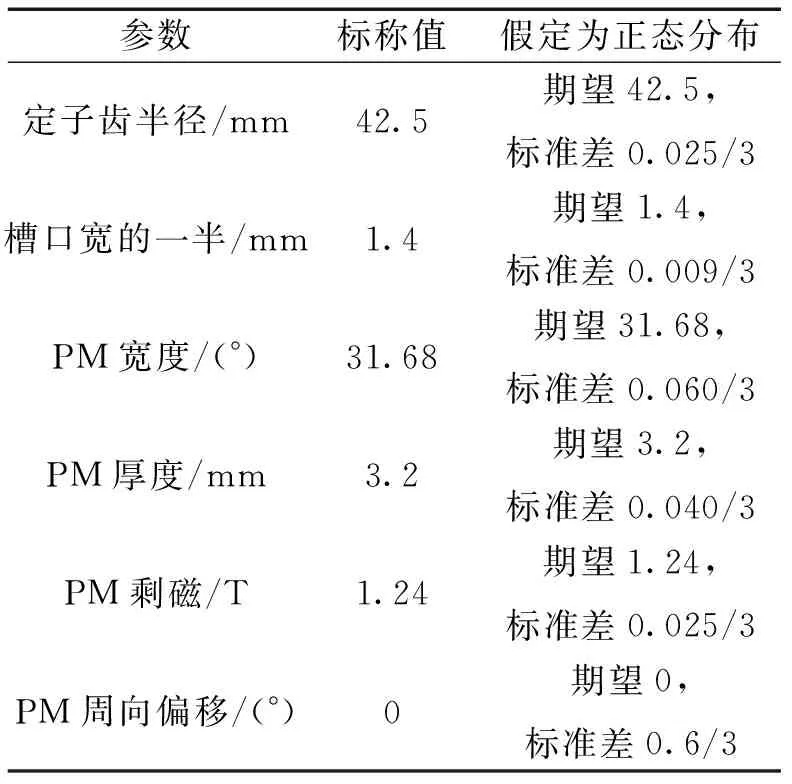
表5 加工误差分布

根据各类误差的概率分布，随机生成300组考虑加工误差的参数样本，如图10所示，并将各组误差样本进行随机组合，建立相应的不对称有限元模型，计算各模型的齿槽转矩。

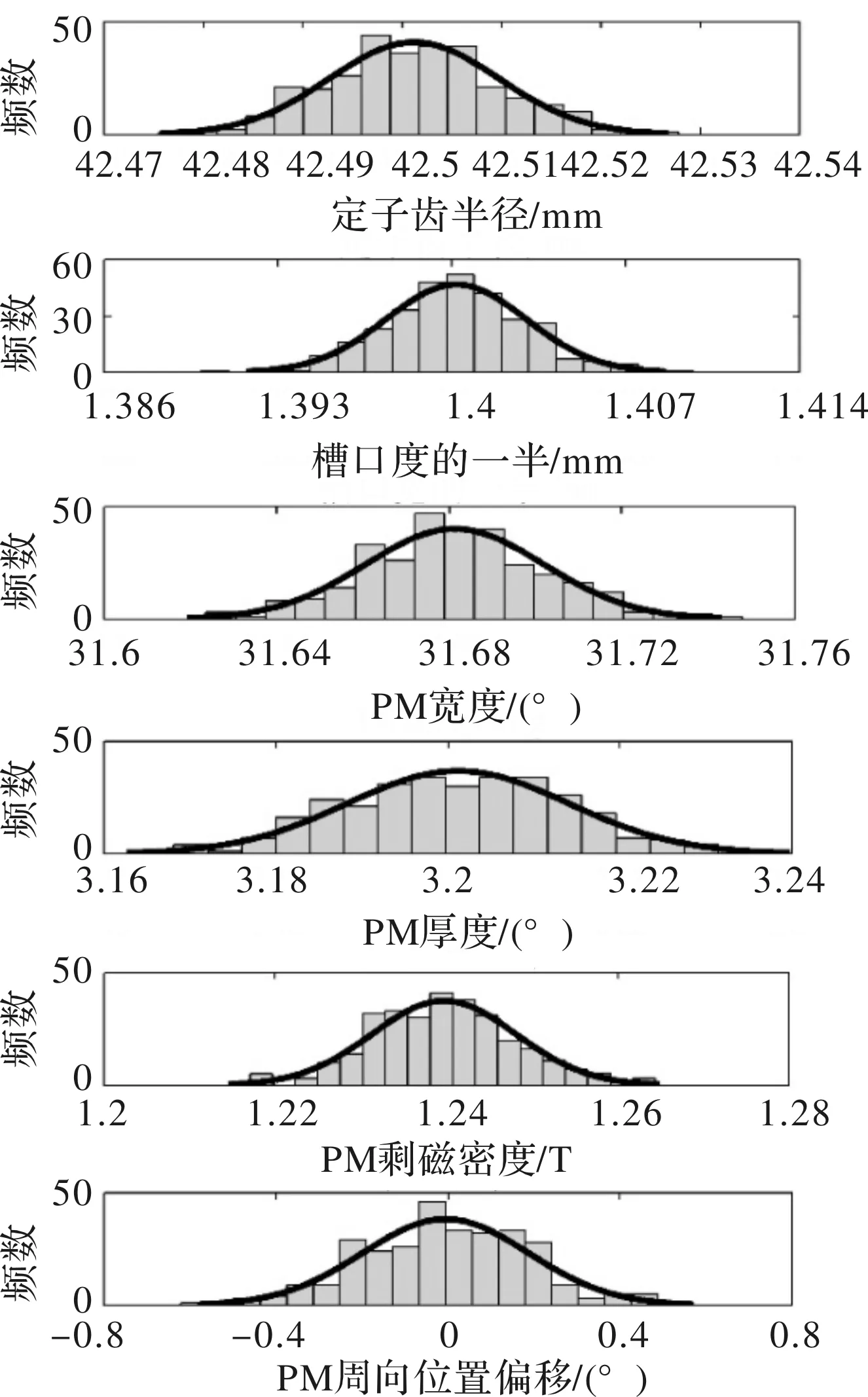
图10 误差样本

对有限元仿真结果进行统计分析，齿槽转矩幅值与谐波分布分别如图11、图12所示。考虑加工误差后，产生了TAHC，使得所有样本齿槽转矩幅值均大于理想模型的19 mNm，且齿槽转矩幅值分布范围很广，从25 mNm到58 mNm。TAHC谐波主要包括定子侧误差产生的10次谐波和转子侧误差产生的12次、24次谐波。其中12次谐波的分布范围最广，从0.8 mNm到35.5 mNm，是导致齿槽转矩幅值分布范围广的主要原因。并且根据能量法模型中的分析，齿槽转矩12次谐波分布范围广是由PM周向位置误差导致的，再次印证了提高永磁体周向位置加工精度是抑制齿槽转矩的有效措施。60次齿槽转矩谐波幅值分布在16.5 mNm到19 mNm，即加工误差对60次齿槽转矩谐波即TNHC影响很小。

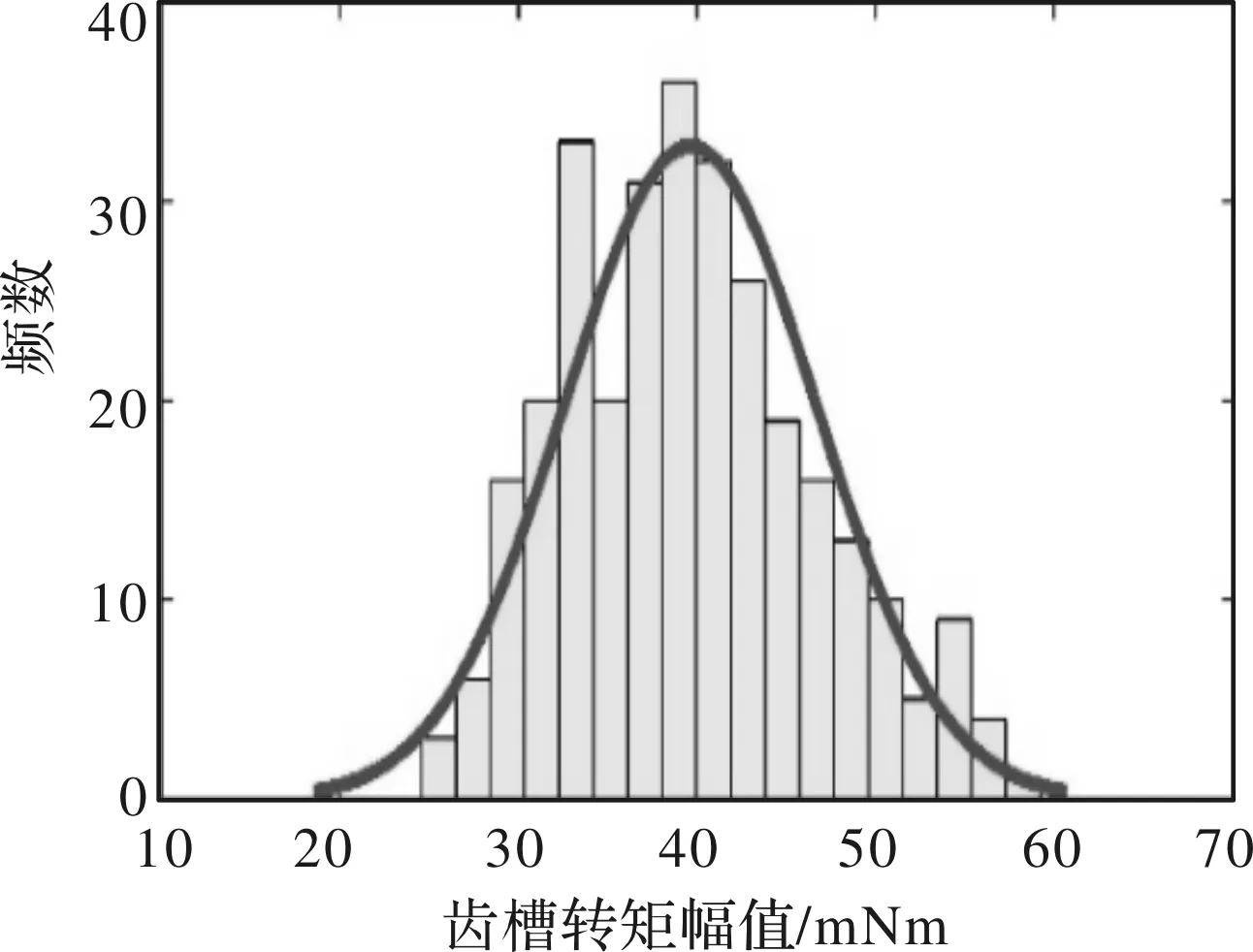
图11 齿槽转矩幅值分布

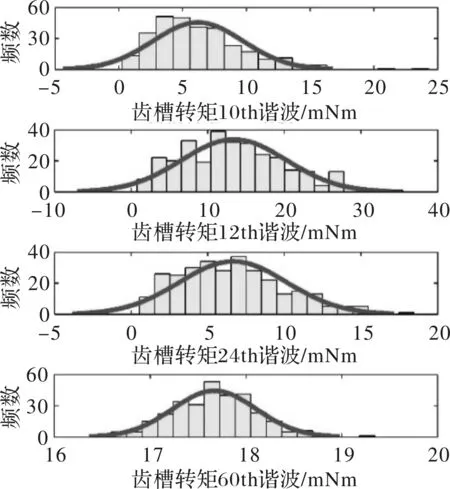
图12 齿槽转矩谐波分布

3 定子冲片循环旋转

在定子冲片叠压过程中，下一片冲片总是相对于前一片定向旋转一个固定的槽数，如图13所示。这样，每一个定子冲片与转子相互作用产生的齿槽转矩都有一个相位差，通过旋转合适的槽数，就能削弱特定极数倍数次的齿槽转矩谐波。

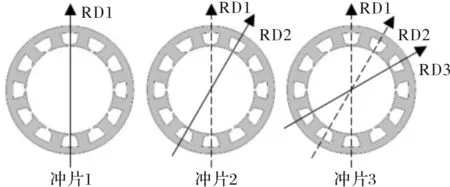
图13 定子冲片循环旋转

对于任意槽极配合的电机，设其定子槽数为Z，转子极数为P，定子侧加工误差导致的齿槽转矩谐波为P的倍数次，P次谐波对应幅值为KP。设单元电机数为Nu=GCD(P,Z)，即槽数与极数的最大公约数。记Z′=Z/Nu，P′=P/Nu，采用定子冲片循环旋转方法，设每次旋转一个槽对应的角度，记第一片冲片的齿槽转矩P次谐波为

TP次-第一片=KPsin(Pα)

(11)

根据正弦函数的性质，相邻Z′片定子冲片的齿槽转矩P次谐波之和为

(12)

若Z′不是质数，设a为Z′的一个因数，且Z′=a*b，定子冲片旋转时，设每次旋转a个槽对应的角度，当b不为1时，相邻b片定子冲片的齿槽转矩P次谐波之和为

(13)

由上可知，当单元电机槽数不是质数时，旋转的槽数将有多种选择，每片定子冲片旋转a个槽，相邻b片冲片的齿槽转矩P次谐波就能相互抵消。同理，仍设定子冲片依次旋转a个槽，c为正整数，相邻b片定子冲片齿槽转矩cP次谐波之和为

(14)

当cP′/b不为整数时，相邻b片定子冲片齿槽转矩cP次谐波才能抵消。因此，b应取最大值Z′，才能使得更多极数倍数次齿槽转矩谐波被抵消，得到最佳的齿槽转矩抑制效果，对应定子冲片依次旋转1个槽。

综上所述，任意槽极配合的电机均能采用定子冲片循环旋转方法抑制极数倍数次齿槽转矩谐波，且定子冲片依次旋转1个槽能取得最好的齿槽转矩抑制效果。实际加工时也采用这种方案。

对于本文研究的12槽10极电机，定子侧误差产生的是10的倍数次齿槽转矩谐波。单元电机槽数为6，极数为5，定子冲片依次旋转1个槽，那么c可取值1、2、3、4和5，即相邻6片定子冲片齿槽转矩10、20、30、40和50次谐波之和都等于0。

对考虑加工误差的有限元模型应用定子冲片循环旋转方法，并忽略冲片间的不一致性，得到齿槽转矩幅值分布如图14所示，齿槽转矩谐波分布如图15所示。定子冲片循环旋转之后，齿槽转矩幅值分布从21 mNm到52 mNm，数学期望为33 mNm，比普通定子电机的40 mNm减小了17.5%。齿槽转矩10次谐波基本上消除了，12次、24次和60次没有变化。

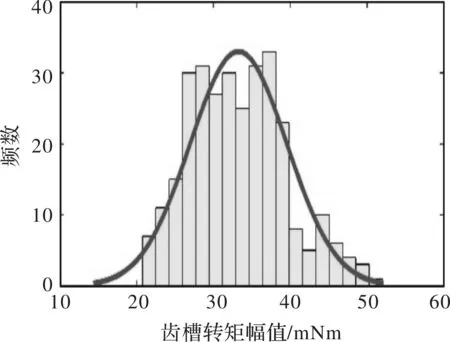
图14 齿槽转矩幅值分布(定子冲片旋转)

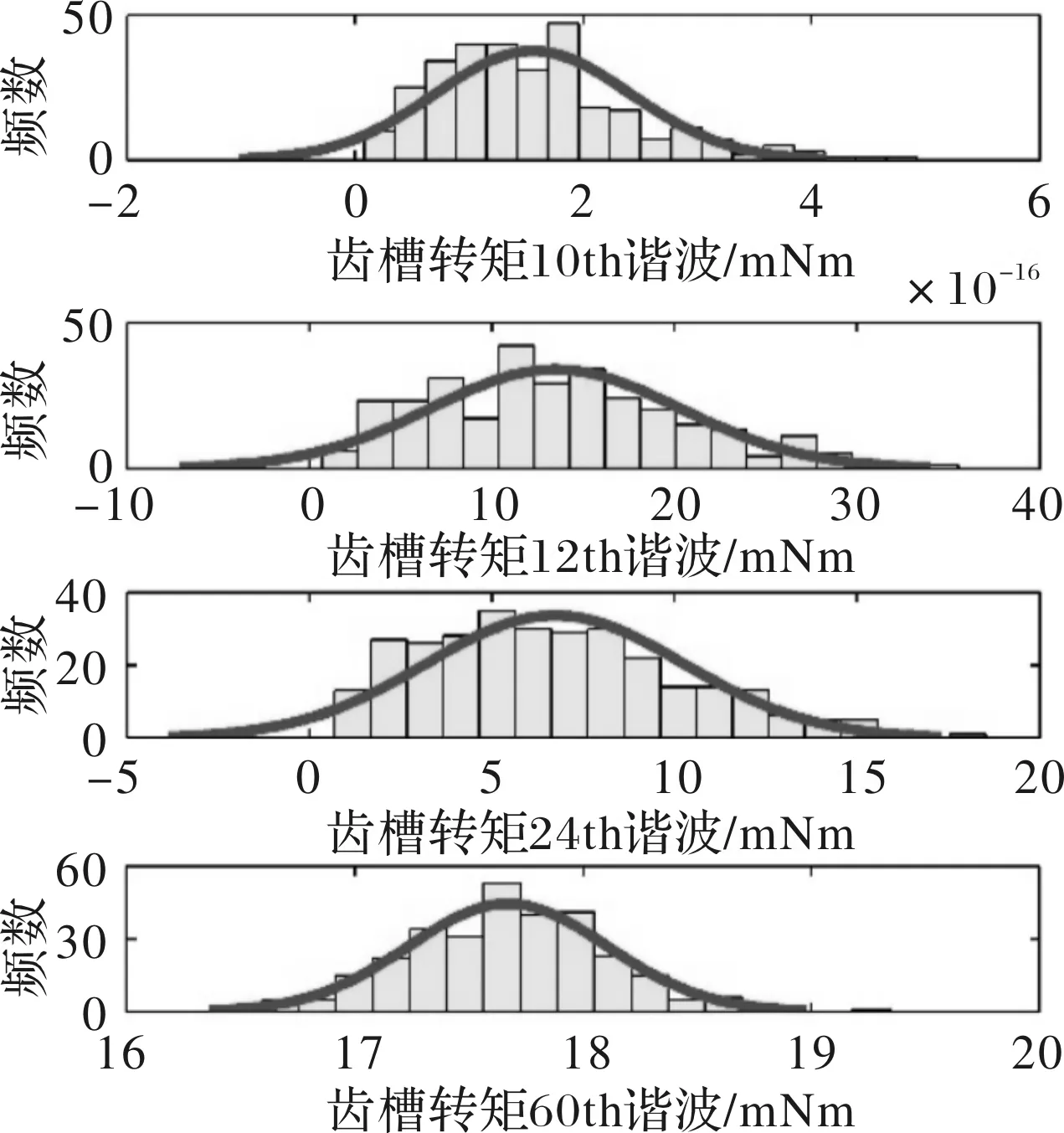
图15 齿槽转矩谐波分布(定子冲片旋转)

采用定子循环换位后和未采用循环换位的齿槽转矩概率分布对比如图16所示，可以看出通过循环换位后齿槽转矩的分布整体向较小的幅值区间偏移，其数学期望相比换位前减小了17.5%，且在齿槽转矩幅值较高的分布区间的频数均有所减小，说明采用定向旋转冲片的方法可以在不提升加工精度的情况下，较好地抑制定子侧加工误差引入的齿槽转矩谐波，进而抑制总的齿槽转矩；另外，循环旋转叠压的定子冲片内圆呈波浪纹，清晰地显示了冲片内径加工误差。普通叠压定子冲片内圆光滑，即冲片旋转之前相同定子齿下的冲片内径一致，这样才能保证旋转之后有较好的齿槽转矩抑制效果。

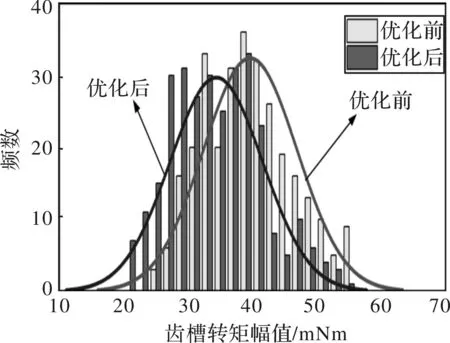
图16 优化前后齿槽转矩幅值对比

4 实 验

从生产的一批电机中随机抽取样本进行齿槽转矩测试，测试平台如图17所示。齿槽转矩测试结果如图18所示，齿槽转矩幅值约为40.4 mNm，与定子冲片循环旋转有限元模型计算的21 mNm至52 mNm相符。傅里叶分解得到的额外齿槽转矩谐波主要是12次，与能量法模型和有限元模型的分析结果一致。极数倍数次齿槽转矩谐波幅值均较小，验证了定子冲片循环旋转方法的可行性。

图17 齿槽转矩测试平台

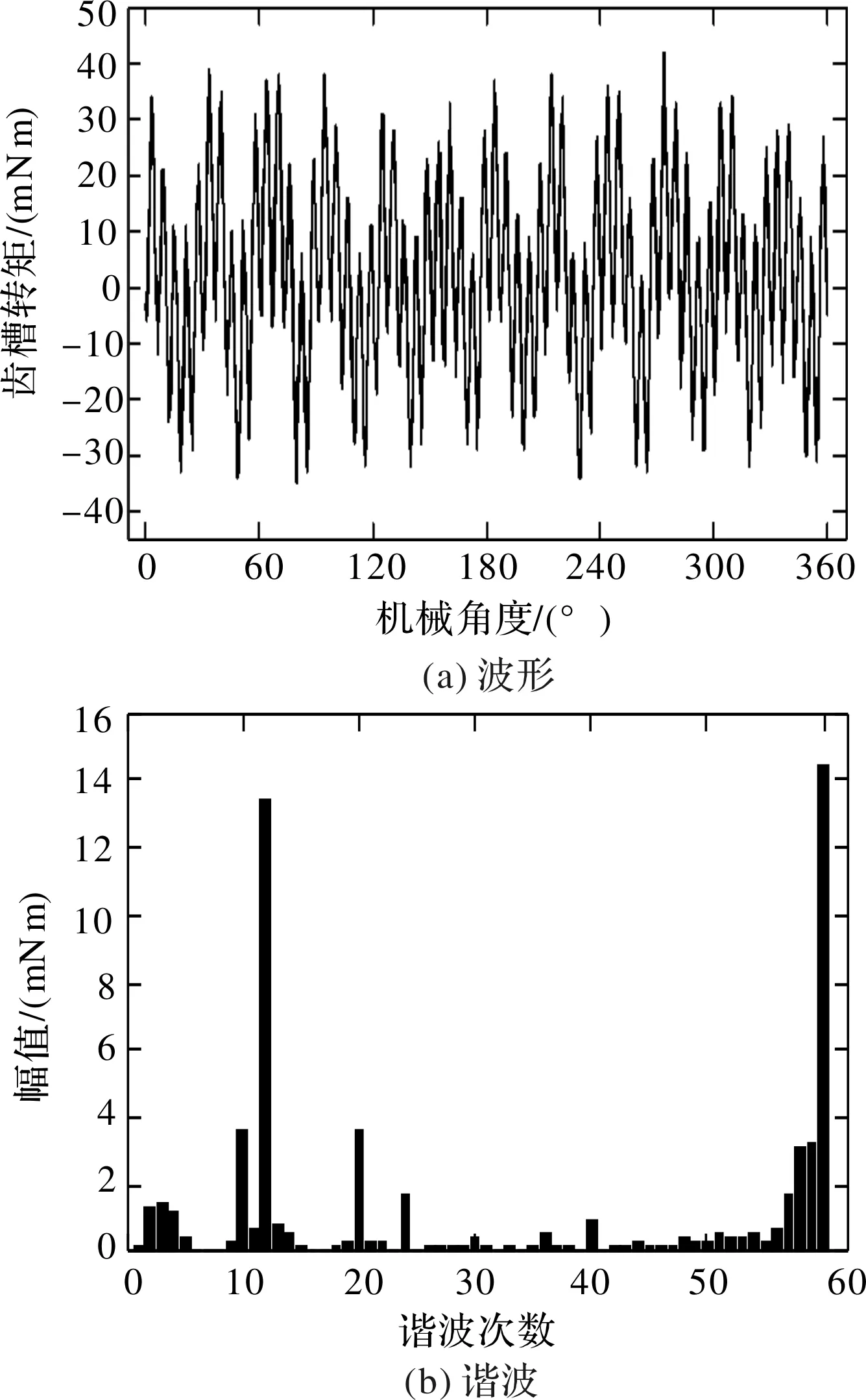
图18 实测齿槽转矩

5 结 论

本文针对有加工误差的表贴式永磁伺服电机进行研究分析，主要得到如下结论：

(1)基于能量法，建立的计及加工误差的表贴式永磁伺服电机齿槽转矩解析模型，能分别评估齿槽转矩对永磁体剩磁、厚度、宽度及周向位置等误差的敏感性大小。解析计算结果表明，永磁体周向位置误差对齿槽转矩影响最大。实际生产中，若加强对该参数的加工精度，可取得较好的齿槽转矩抑制效果。

(2)对任意槽极配合电机，均能采用定子冲片循环旋转方法削弱定子侧误差产生的额外齿槽转矩，并且相邻冲片依次旋转一个槽距能取得最好的齿槽转矩抑制效果。

(3)基于蒙特卡罗方法，利用有限元软件，建立的一套计及实际加工误差的分析体系，能较好地预测批量生产永磁伺服电机齿槽转矩及其频谱分布规律，用于指导电机生产。