一种FLL 辅助PLL 的GNSS 接收机矢量跟踪环路
刘 卫,牟明会,顾明星,胡 媛,王胜正
(1.上海海事大学 商船学院,上海 201306;2.上海海洋大学 工程学院,上海 201306)
0 引 言
全球导航卫星系统(Global Navigation Satellite System,GNSS)已广泛应用于军事和民用领域,成为最受用户欢迎的导航方法之一。GNSS 接收机设计主要包括捕获、跟踪、解算三个环节,跟踪环节逐步精细估计载波频率和码相位值,获取伪距、伪距率信息,在解算环节结合卫星位置解算出接收机位置、速度、时间信息。传统的GNSS 跟踪环路是借助载波跟踪环路(简称载波环)和码跟踪环路(简称码环)完成的,其中码环实现形式通常表现为延迟锁定环路(DLL),而载波环通常有相位锁定环路(PLL)和频率锁定环路(FLL)两种。然而,动态环境中的GNSS 环路跟踪存在载波频率和码频率波动问题,大幅度的频率波动会影响跟踪性能,从而直接影响导航定位效果。
GNSS 环路滤波器以比例积分滤波(PIF)为主,其利用载波相位差或载波频率差,结合环路滤波参数及相干积分时间确定当前时刻最佳相位或频率,从而完成环路跟踪。GNSS 环路跟踪精度主要受热噪声和动态应力误差两部分因素影响,相较于PLL,FLL 能更加鲁棒地容忍用户的动态应力,能跟踪信噪比更低的信号,然而,FLL 输出的载波相位测量值不够精确,并且数据解调过程中发生的比特错误率更高。综合考虑到PLL 与FLL 优缺点,文献[5]将FLL 与PLL 结 合 起 来,以FLL 辅助PLL 的方式估计载波频率,经过稳定状态下的功率谱分析、均值及方差比较,结果表明FLL 辅助PLL 的环路跟踪方式能在环路噪声与载体动态性之间做出平衡,从而优化环路跟踪性能。但缺点是载体运动参数需要根据接收机所处环境的信噪比、动态应力情况预先调整,这制约了该环路结构在实时场景下的应用。
为了充分利用跟踪环节中的环路状态量,更具有普遍适应性的矢量跟踪(Vector Tracking,VT)被提出。不同于传统的标量跟踪,VT 结构将GNSS 跟踪环节和解算环节紧密相连,利用载波频率差、码相位差,计算伪距差、伪距率差,通过导航滤波更新导航结果,并将导航结果送入跟踪环路,实现所有通道之间的信息共享。矢量跟踪结构自提出以来,经过不断发展,文献[7]以VT 为基础,将载波环输出的多普勒频移信息和码环输出的码相位信息送入导航滤波器进行导航解算,并利用解算环节的伪距信息实时更新码频率,辅助环路跟踪。但其载波环路实现形式仍然是单一的PIF 环路,动态环境中GNSS 载波相位或频率测量值精度低,易造成环路失锁并影响定位结果。
为改善动态环境中载波频率和码频率的波动问题,提高定位精度,本文提出一种FLL 辅助PLL 的GNSS 矢量跟踪结构。首先确定导航跟踪与导航解算的系统模型,包括FLL 辅助PLL 的载波跟踪环路结构设计、矢量码环结构设计和导航解算部分的卡尔曼滤波(KF)状态模型和量测模型。实验结果表明,相较于传统的标量跟踪方法,本文所提出的FLL 辅助PLL 的矢量跟踪方法能够在动态环境下输出较小的载波频率和码频率误差,且具有更高的定位精度。
1 标量跟踪结构
传统的标量跟踪结构如图1 所示。接收的射频信号经过降频量化后,转化为数字中频信号()。每个通道的数字中频信号首先与本地载波振荡器复制的载波信号(包括同相支路I 和反相支路Q)进行混频,然后与本地码发生器复制的超前(Early)、即时(Prompt)、滞后(Late)码信号进行相关,经积分-清除后得到相干积分结果。环路鉴别器根据6 个相干积分结果可以估算出载波相位差和码相位差,并由环路滤波后作为载波数控振荡器(NCO)和码NCO 的控制输入。标量跟踪结构的码环为DLL,载波环为PLL 或FLL。如图1 所示,每个跟踪通道之间相互独立,伪距差、伪距率差被送入导航解算部分,通过KF 实现导航信息解算。

图1 标量跟踪结构
2 矢量跟踪结构
本文提出的FLL辅助PLL的矢量跟踪结构如图2所示。

图2 FLL 辅助PLL 的矢量跟踪结构
载波环部分通过FLL 辅助PLL 的形式更新载波相位值,控制载波NCO 的输入从而保持环路锁定。其中,PLL 采用三阶环路滤波,FLL 采用二阶环路滤波。码环矢量结构以KF 为导航处理器,将导航解算部分的伪距信息反馈到码NCO,调整各跟踪通道的码频率,以此跟踪GPS 伪码信号并实现所有通道的信息共享。对于导航滤波器,除码环输出的码相位信息外,载波环滤波输出的多普勒频移信息也送入KF 中,计算接收机位置、速度、时间信息。
2.1 载波环结构设计
载波环结构设计包括三阶PLL 设计、二阶FLL 设计和FLL 辅助PLL 设计共三部分。PLL 和FLL 设计均采用PIF 形式,分别更新环路状态量,最后通过线性组合获得载波相位值从而控制载波NCO 输入。
2.1.1 三阶PLL 设计
PLL 是以锁定输入信号载波相位为目标的一种载波环实现方式。基于PIF 的三阶PLL 通过预测载波相位、载波角频率和载波角频率率(载波角频率的变化率)实现载波信号的跟踪锁定。
载波相位鉴别器鉴别时刻的载波相位差Δθ:

式中:I和Q分别表示时刻即时同相支路和正交支路的相干积分值。
三阶PLL 结合当前时刻的状态量x,计算下一时刻的状态量x:


2.1.2 二阶FLL 设计
FLL 是以锁定输入信号载波频率为目标的一种载波环实现方式。基于PIF 的二阶FLL 通过预测载波频率和载波频率率(载波频率的变化率)实现载波信号的跟踪锁定。
载波频率鉴别器鉴别-1 和两相邻时刻的角频率差Δϖ:

二阶FLL 结合当前时刻的状态量x,计算下一时刻的状态量x:
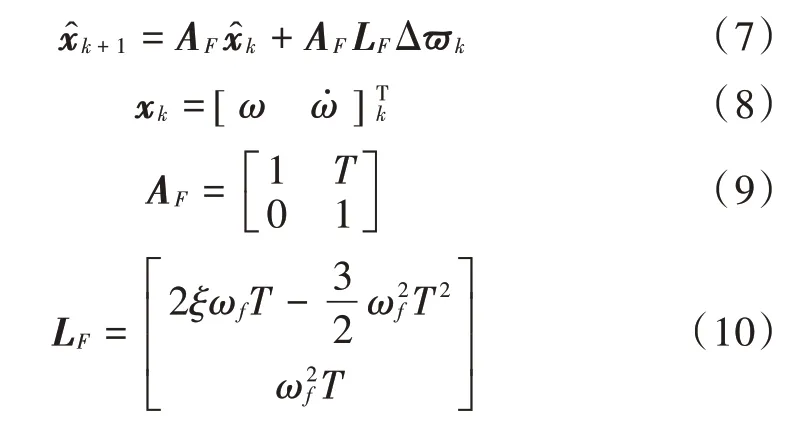
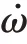
2.1.3 FLL 辅助PLL 设计
时刻三阶PLL 参与反馈到载波NCO 的值为:

时刻二阶FLL 参与反馈到载波NCO 的值为:

通过线性组合,得到最终反馈到载波NCO 的载波相位为:

通过更新的载波相位值,反馈到载波NCO 复制出本地载波信号,与输入信号混频实现载波稳定跟踪。
2.2 矢量跟踪环设计
码相位鉴别器鉴别接收码和复制码之间的码相位差Δτ:

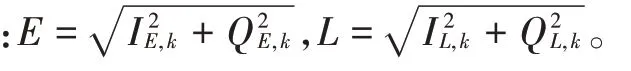
码相位差Δτ经线性转换得到伪距误差Δ:

式中:为卫星信号被发射时的码频率,其值为1.023 MHz。
利用KF 计算当前时刻接收机的位置、接收机钟差Δ,结合星历解算出的卫星位置、卫星时钟钟差Δ、电离层延时、对流层延时、伪距量测噪声量ε,计算当前时刻的伪距值:
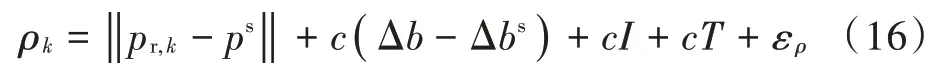
计算时刻的码频率值:

通过更新的码频率反馈到码NCO,调整各跟踪通道的码频率实现所有通道的信息共享。
2.3 导航解算
为了计算接收机的位置、速度、时间信息,并对跟踪过程与解算过程建立联系,选取KF 作为导航滤波器。KF 包括状态模型和量测模型两部分,具体理论如下。
KF 状态量为:

状态模型为:

状态转移矩阵为:
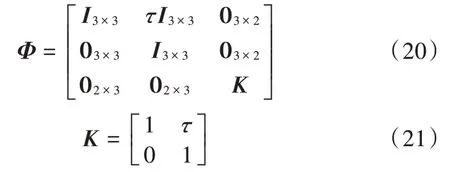
式中为KF 更新时间间隔。
量测量由跟踪环路测得的伪距误差Δ、伪距率误差Δ˙构成。

KF 的量测模型为:

其中:

式中:1,2,…,表示参与定位的卫星代号;[I,I,I]是卫星在接收机处的单位观测矢量。
3 实验和结果分析
3.1 实验数据采集
为了验证所提出的FLL 辅助PLL 的矢量跟踪结构相较于传统的标量跟踪结构有更好的跟踪性能和定位性能,本文进行了动态实验验证。在本实验中,中频信号采集器采集GPS 的L1 波段信号并转换为频率为3.996 MHz 的中频信号,采样频率为16.369 MHz。
实验装置如图3 所示,天线设备安装在电瓶车车筐顶端,电源和中频信号采集器在车筐内。实验在上海海事大学掷球场跑道进行,实验时长为150 s,实验场地如图4所示。

图3 实验装置

图4 实验场地
3.2 实验结果分析
根据所提出的FLL 辅助PLL 的矢量跟踪环路结果进行实验数据处理,分别对卫星信号的载波频率、码频率和定位结果三个参量进行对比分析。
图5 和图6 给出了环路跟踪的载波频率和码频率对比结果,灰色点代表传统的标量跟踪结果,黑色点代表本文提出的FLL 辅助PLL 的矢量跟踪结果。
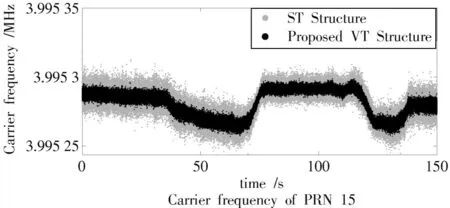
图5 载波环

图6 码环
载波频率标准差分别为10.663 1 m,9.632 3 m;码频率标准差分别为4.011 1 m,1.832 6 m。从图5、图6中可以看出,动态环境下所提出的FLL 辅助PLL 的矢量跟踪方法相较于传统标量跟踪方法具有更高的跟踪精度,GNSS 跟踪环路输出的载波频率和码频率波动性明显更小。载波环精度提高是因为FLL 辅助PLL 的载波跟踪方式可以更稳定地跟踪载波信号。码环精度提高是因为矢量跟踪结构的码频率是通过导航解算部分的伪距信息预测的,相较于传统的标量跟踪精度更高。标准差计算公式为:

图7 对比了两种方法的定位结果,星形标号代表传统的标量跟踪方法输出的定位结果,小圆圈代表本文提出的FLL 辅助PLL 的矢量跟踪方法输出的定位结果。运动过程中,前者的球概率误差(SEP)为51.637 3 m,后者的SEP 为3.372 6 m。从图7 中可以看出,使用传统的标量跟踪方法解算出的定位结果较为分散,定位结果甚至分布在掷球场中央,部分结果的高度也不正确,而采用FLL辅助PLL的矢量跟踪方法所得的定位结果轨迹效果明显更好,定位精度更高。SEP计算公式为:
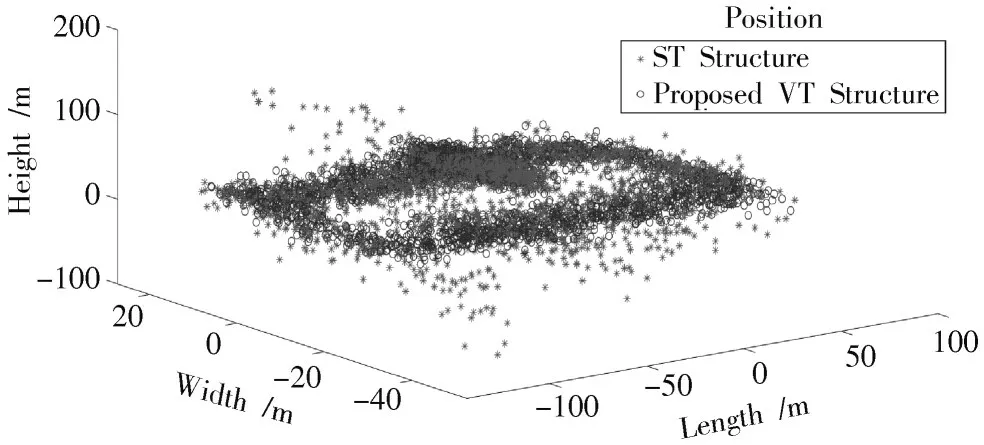
图7 定位结果
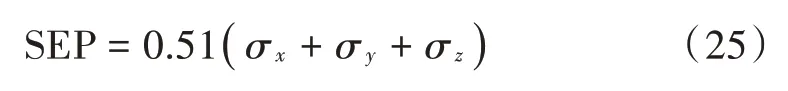
式中:σ为东向标准差;σ为北向标准差;σ为天向标准差。
4 结 论
本文提出了一种FLL 辅助PLL 的矢量跟踪方法,并通过实验验证了该方法的跟踪及定位性能。分别对所提出方法与传统方法的载波跟踪频率、码频率、定位结果三个参量进行对比分析。实验结果表明,相较于传统的标量跟踪方法,本文提出的FLL 辅助PLL 的矢量跟踪方法能够在动态环境下输出较小的载波频率和码频率误差,且具有更高的定位精度。

