降低OFDM 系统PAPR 的LDPCSS-GA 方法

林志阳

（海南大学 信息与通信工程学院，海南 海口 570228）

0 引 言

正交频分复用（OFDM）采用多载波调制技术，具有高数据传输速率和抗窄带干扰能力，与其他多载波技术相比，其带宽利用率高，可增加系统容量还能提供可靠的传输，能适应第五代（5G）宽带无线通信网络。但OFDM 系统的主要缺点之一在于高峰均功率比（PAPR），因为信号通过某些非线性设备传播时，高PAPR 可能会导致带内失真和带外辐射，从而导致系统误码率性能下降。

目前，研究降低OFDM 系统PAPR 的方法有很多，大致可分为两类：一类是信号失真技术，如削波、滤波和星座扩展等。削波技术是将信号削波到预定的阈值以下，对于OFDM 系统，很容易产生带内失真和误码率升高，星座扩展是无失真技术，但会增加发射信号的能量。第二类包括信号加扰技术，如选择性映射（SLM）是在多信号表示方法的基础上，具有与编码、星座扩展相似的特性，且需要发送边信息，会产生较高的计算复杂度和降低带宽效率。部分传输序列（PTS）是PAPR 降低研究最广泛的技术，也是无失真的一种方法。由于PTS 方法将相位因子信息作为辅助信息发送到接收机，会导致传输效率降低且增加了系统复杂性，文献[6-7]采用GA 遗传算法对旋转因子进行优化，PAPR 性能降低了，但在接收机上需要附加相关技术来恢复发送的OFDM 信号。

文献[8]采用循环移位序列（CSS）方法，CSS 方法是从PTS 方法发展而来的，它将OFDM 信号子序列循环移位并组合后替代OFDM 信号序列，通过循环移位序列而不是将旋转因子乘以OFDM 信号子序列，不管从PAPR降低还是系统性能上，CSS 方法比PTS 方法更好。

OFDM 系统另外一个主要缺点是在衰落环境中的BER 性能差，导致接收器不可能无错误地检测到所有子载波。为了减小衰落的影响，文献[9]采用LDPC 编码技术实现OFDM 系统。文献[10]将Turbo 编码技术应用到OFDM 系统中，虽然Turbo 码在编码过程中比LDPC 码简单，但在译码时比LDPC 码复杂得多，而LDPC 码具有较强的纠错能力和抗突发差错。文献[11]采用遗传算法（GA）优化LDPC 码，GA 的特点在于能解决高维优化问题，不仅能找到局部最小值，且选择恰当的参数能很快收敛并获得最优解，常用于人工智能、信道编码和LDPC译码器等领域。

综上所述，本文提出了一种对LDPC 码和CSS 联合编码的方法（称为LDPCSS 码），即将CSS 和LDPC 码作为前期编码阶段，然后导出LDPC-CSS 码的奇偶校验矩阵，通过奇偶校验矩阵，使用置信度传播算法（BP）和GA 算法进行联合译码。

1 LDPCSS 联合方法的编译码

1.1 OFDM 系 统 的PAPR 计 算 方 法

OFDM 信号由多个独立调制的子载波组成，当相互叠加时，会产生较大的PAPR，当个信号以相同相位叠加时，所产生的峰值功率是平均功率的倍，在时间间隔中传输的信号()的PAPR 定义为：

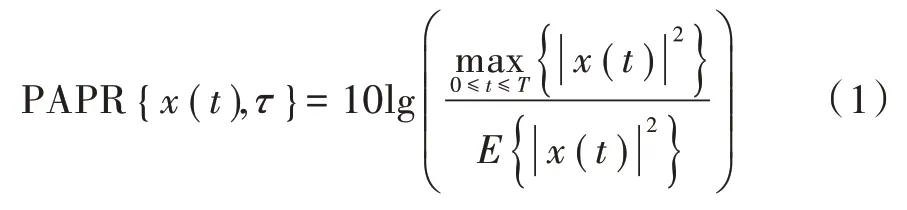
式中：max{·}表示峰值信号功率；{·}表示平均信号功率。

为了计算更精确的PAPR 值，应考虑更多符号，否则可能会省略一些峰值，从而导致PAPR 值错误，可通过对()进行过采样来解决，用互补累计分布函数（CCDF）定义峰均值超过某一门限值的概率：

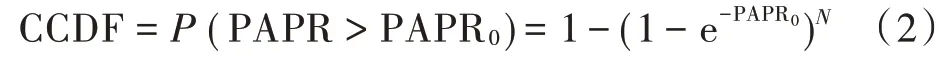
式中PAPR表示某个限幅电平的PAPR 值。

1.2 基 于LDPCSS-GA 的OFDM 系 统

图1 基于LDPCSS 码的OFDM 系统

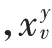
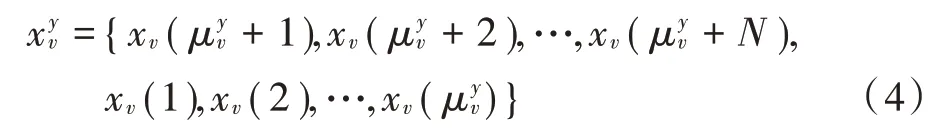
由文献[12]可知，循环移位操作不会破坏输入符号序列之间的正交性，因时域中的循环移位等效于在频域中乘以相应的线性相位矢量。因此，当获得校验矩阵后，可根据校验矩阵进行编码，从而得到相应的码字，R(=1,2,…,)表示循环移位后的行向量，经CSS处理后，原始的LDPC码字被分割为个向量，即，…，R，长度为（v=1,2,…,），并得到相对应的行向量() ，表示为()，()，…，() 。根据CSS 和以上假设，则：

式中⊕表示模2 加法运算。

本文将作为等效传输码字，将LDPCSS 码字定义为由等效传输码字和循环移位组成的码字。

定义1：先前描述的OFDM 系统的LDPCSS 码是具有以下码字的分组码，它的矢量表示为：

1.3 PAPR 减小和LDPCSS-GA 算法

本文减小系统PAPR 值采用文献[12]的交织分区以及制定的标准2 生成的偏移集，如果满足：

其中：1 ≤≠≤，1 ≤≠≤，表示子载波数，表示子块数，且满足=W，为旋转因子数。考虑LDPCSS 码的优化问题，在设计过程中，尽量降低系统PAPR、误码率和复杂度，因此应用了遗传算法。遗传算法是一种常用的函数优化方法，它具有全局搜索能力，可获得最佳或更好的近似解。

LDPCSS-GA 算法基本思想如下：

1）初始化：种群大小，编码率，码长，设置最大迭代次数。

2）for=1,2,…,do

3）更新种群：将父代向量的第一行与父代向量的第二行相结合生成下一代向量，交叉率=1。将下一代的随机位置上0 →1生成为，突变率=1。为了恢复编码率，对产生的后代向量进行突变，产生向量作用于群体，并更新种群。

4）计算适应度函数：LDPC译码是基于Tanner图的消息传递迭代译码，采用置信传播译码算法（BP）沿Tanner图的边传递概率值，对位节点的判据采用其概率值组合。

6）end for

8）结束

2 仿真分析

通过概率密度演化方法得到最大变量节点度分布，并构造和优化奇偶校验矩阵，仿真中发射机不发送循环移位序列，接收机采用BP 算法。

图2显示了不同方法降低系统PAPR的性能比较，相关的参数设置见表1。在CCDF 为10时，本文采用的LDPCSS 联合方法降低系统PAPR 约5.7 dB，相比文献[9]方法降低约0.1 dB，且明显优于其他方法。

图2 不同方法降低系统PAPR 的性能比较

表1 相关参数设置

图3显示了不同方法的BER 性能，为了与文献[9-10]的BER 性能比较，设置码率为1 2，约束长度为4，输入回退为3，=512，在AWGN 信道中采用16QAM，可以看出，本文采用的方法在传输信号的PAPR 值较大时，BER 性能下降很小，随着子载波和星座数增加，BER 性能明显优于文献[9-10]方法。

图3 不同方法的BER 性能比较

图4 显示了原始OFDM 信号和采用CSS 处理后，当子载波数=8，16，32 和64，CCDF=10时，经过CSS处理后的PAPR 分别降低了约6.2 dB，6.6 dB，7.1 dB 和7.7 dB。

图4 不同子载波对PAPR 性能的影响

图5 显示采用LDPCSS-GA 方法的PAPR 平均值分析，其中种群大小设置为20，50 和100，在10～100 之间取值，可以看出种群数在20～100 时，平均PAPR 的值相差0.2 dB，显然种群数为20 比较合理。

图5 不同G 对系统平均PAPR 的影响

3 结 语

本文提出了一种基于LDPCSS 码的奇偶校验矩阵，并使用BP 算法对LDPC 码字和循环移位因子进行联合译码，通过GA 算法不仅降低了OFDM 系统的PAPR，且经过优化后的LDPC 码，既降低了BP 译码器的译码复杂度和延迟（因为不需要传输辅助信息即循环移位因子，也不需要在译码前对其进行估计），又在误码率性能方面得到了提升。仿真结果表明，本文所采用的LDPCSSGA 方法与其他方法比较，有效降低了PAPR 和计算复杂度。由于需要进一步降低了PAPR，因此，在未来研究中，如何提高译码的收敛速度且不降低纠错能力仍是一项重要的工作。