深度残差网络模型的构建及其在糖尿病预测中的应用

左星光，范 静

（1.上海第二工业大学 工学部，上海 201209；2.上海第二工业大学 文理学部，上海 201209）

0 引 言

随着计算机科学与医学的融合发展，基于机器学习和神经网络模型的疾病预测已成为临床医学诊疗的重要辅助手段，这也包括了对糖尿病的预测研究。由于糖尿病受到很多因素的影响，包括患者的遗传、生活方式、环境等，还可能引发心脏病、脑血管疾病等并发症。因此，急需建立高准确率的糖尿病预测模型，对普通人的糖尿病发病概率进行预测，以确定高危人群范围，从而有效地控制糖尿病的发病率。

目前，已有多篇文献利用神经网络对糖尿病进行预测研究。文献[5]使用SPSS 软件分析人工神经网络的统计量，得出人工神经网络用于糖尿病预测是有实际意义的，并比较了人工神经网络、支持向量机模型和集成学习AdaBoost 在糖尿病预测中的性能，结果显示，人工神经网络的性能最佳。文献[6]构建了神经网络模型，得到83%的糖尿病预测准确率。文献[7]使用Stacking 方法集成了逻辑回归、随机森林、支持向量机、极端梯度提升4 种算法建立了糖尿病预测模型，取得了85%的预测准确率。文献[8]提出了一种新的基于迭代提升欠采样的集成分类方法，通过从多数类样本中进行欠采样，形成弱分类器，最后用加权组合方式将弱分类器组合成一个强分类器。通过该采样方法，在西医和中医两种多标签数据集上，准确率分别提升了6.30%和12.43%。文献[9]基于网格搜索和交叉验证的支持向量机算法建立了糖尿病并发症预测模型，结合网格搜索算法在指定区间搜索最佳惩罚因子和径向基核函数的方差，将糖尿病并发症的预测准确率提高到92%。文献[10]对比了卷积神经网络、全连接神经网络、决策树模型和基于XGBoost 的梯度下降树模型在糖尿病预测中的性能，使用的数据集为某医院的糖尿病患者临床检查数据及其诊断结果。结果显示，全连接神经网络的准确率最高，达到了78.10%。

然而由于疾病本身的复杂性以及不同患者的身体指标存在差异，致使疾病预测准确率仍需提高，疾病预测方法仍需完善。本文构建了深度残差网络模型，解构了残差块的结构，比较了不同的激活函数和优化算法对模型性能的影响，进而，针对UCI 糖尿病数据进行了预测，并与多个糖尿病预测模型进行了对比分析，最后，总结了深度残差网络模型的优缺点。

1 深度残差网络模型

深度残差网络模型是基于神经网络构建的。神经网络是一种模拟人脑工作原理，从而实现类人工智能的机器学习技术，支持处理图像、文本、语音以及序列多种类型的数据，可以实现分类、回归和预测等。神经网络模型发展自美国神经物理学家Frank Rosenblatt 提出的感知机模型。经过学者们不断地研究，神经网络得到了长足的发展：在架构方面，从单层网络演变为多层网络、从无法解决异或问题到能解决几乎任何复杂问题；在神经元激活方面，由最初的阈值比较发展为多种激活函数；在模型优化方面，随机梯度下降（简记为SGD）、Adam 等一系列优化算法被应用到神经网络模型中以更新模型中的参数。

20 世纪90 年代，美国电话电报公司的神经网络研究小组开发了一个用于读取支票的卷积神经网络。文献[12]使用改进的卷积神经网络在ImageNet 挑战赛上大放异彩。自此卷积神经网络的理论与应用得到飞速发展。随着对神经网络模型研究的深入，研究人员发现网络层数越深，模型的性能反而“退化”，同时还出现了参数量陡增、梯度弥散或梯度爆炸等一系列问题。为改善缺陷、提高卷积神经网络的泛化能力，文献[13]设计了深度残差网络（简记为DRN），该模型提出在各层之间引入恒等映射，通过恒等映射拟合残差函数。这一改进能加快网络的训练速度，缓解梯度弥散或梯度爆炸问题，并且可通过增加网络深度来提高准确率，而不会出现“退化”问题。残差网络的出现使训练深层次的神经网络模型成为可能。

下面将从模型的原理、残差块的构造、模型激活函数和优化算法的选择等四方面来详细介绍深度残差网络模型。

1.1 模型的原理

卷积神经网络可以看成卷积层的堆叠，几个卷积层堆叠在一起被称为卷积块。输入数据经过卷积块之后会产生新的数据，即在输入和输出之间存在映射关系。在深度残差网络中，这个映射关系称为underlying mappings，记作()，表示模型输入。图1 是一个典型的残差块结构。通过添加额外的恒等快捷连接，即()=，来自上层的输出可直接添加到当前堆叠块的输出中，并且不用增加额外的参数。

图1 残差块结构

假设多个非线性层可以渐近逼近一个复杂函数，这等价于多个非线性层可以渐近逼近一个残差函数()=()-。因此，第个残差块执行以下计算：

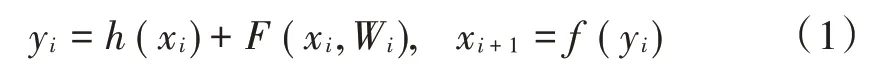
式 中：x，y是 第个 残 差 块 的 输 入、输 出 数 据；W ={W |1 ≤≤}是与第个残差块相关的权重，是残差块中的层数；是待学习的残差函数；函数()为恒等映射：()=；为激活函数，表示数据相加之后要进行的操作。

图2 是本文构建的深度残差网络。

图2 DRN 结构

当也是一个恒等映射，即x=y，利用递推逐项合并，得到第层的输入为：

假设损失函数为，根据反向传播的链式求导法则有：

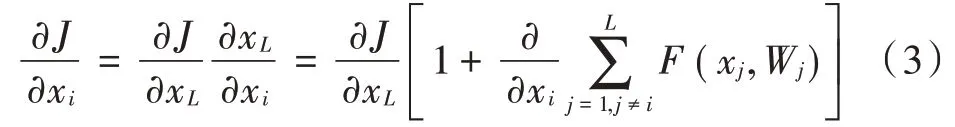
为分析模型性能，本文采用准确率、精度、召回值、值和平均准确率等5 种指标。准确率和平均准确率将被作为主要评估指标。平均准确率为次实验得到的准确率的平均值。准确率定义为预测正确的结果占总样本的百分比，计算公式为：

式中：TP 表示实际是正类的样本数；FP 表示被模型误判为正类的样本数；TN 表示实际为负类的样本数；FN 表示被模型误判为负类的样本数。精度定义为被预测为正类的样本中实际为正类的样本数，计算公式为：

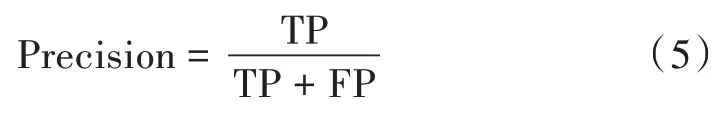
召回值定义为实际为正类的样本中被预测为正类的比例，计算公式为：

值定义为精度和召回值的调和平均数，计算公式为：

1.2 残差块的构造

由于本文利用深度残差网络对糖尿病进行预测，而糖尿病数据集不同于图像数据，数据集中各个特征代表不同的含义，无法应用卷积运算。因此用全连接层替换原来的卷积层。文献[13]证明，在残差块中执行全连接层的操作是可行的。

同时，在残差块中加入了批量标准化层（Batch Normalization）。引入批量标准化，可以降低样本间值域的差异，使得模型中大部分数据处在非饱和区域，保证梯度反向传播的有效性；还可以减少模型参数及其初始值对梯度的影响，从而加快网络的收敛速度。批量标准化也可被看作是一种正则化手段，可使模型减少对Dropout 层的使用。

在批量标准化的计算过程中，假设输入数据为，将其分为大小为的小批数据，每小批数据称为一个batch。对于batch 中的每个样例，批量标准化的计算公式为：

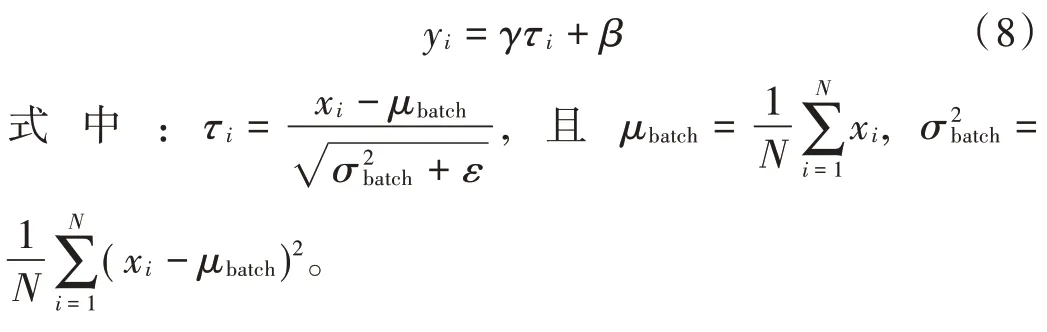
值得注意的是，残差块中各层的排列顺序对模型性能会产生一定影响，不合理的排列顺序可能会导致模型性能的下降。在模型具有相同参数量、学习率、学习轮数的基础上，比较了基于图3 和图4 两种残差块的模型性能。残差块Ⅰ中的BN 层和Dropout 层的位置被排在两个全连接层之后，残差块Ⅱ正好相反。

图3 残差块Ⅰ

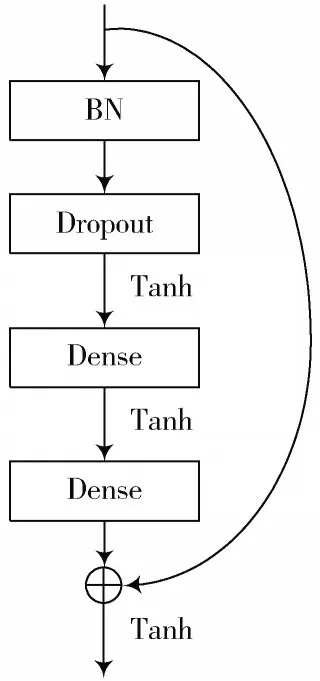
图4 残差块Ⅱ

经过5 次训练后，得出表1 中所列结果。易知，无Dropout 时，基于残差块Ⅰ构建的深度残差网络在5 次训练中准确率、召回值、值、平均准确率均高于残差块Ⅱ，分别提高了4.55%，18.03%，10.29%，3.53%。

值得注意的是，Dropout 层相当于给快捷连接添加了一个缩放。在本文设计的深度残差网络模型中，Dropout 的参数设置为0.5，即把上层传递过来的参数丢弃50%。从表1 的数据可看出，有Dropout 时，残差块Ⅰ的平均准确率仍高于残差块Ⅱ2.36%。综上，残差块Ⅰ的性能优于残差块Ⅱ的性能，残差块Ⅰ中无Dropout 的性能优于有Dropout。因此本文采用残差块Ⅰ的结构，并去除了Dropout 层。

表1 基于残差块Ⅰ和残差块Ⅱ的模型性能对比 %

1.3 激活函数的选择

激活函数是神经网络中对数据进行计算的非线性函数，通过这个非线性函数模拟神经元处理过程。本文针对3 种常用激活函数：ReLU、Sigmoid 和Tanh，在模型具有相同的参数量、训练轮数、批次数量的情况下，对比了它们对模型性能的影响，结果见表2。

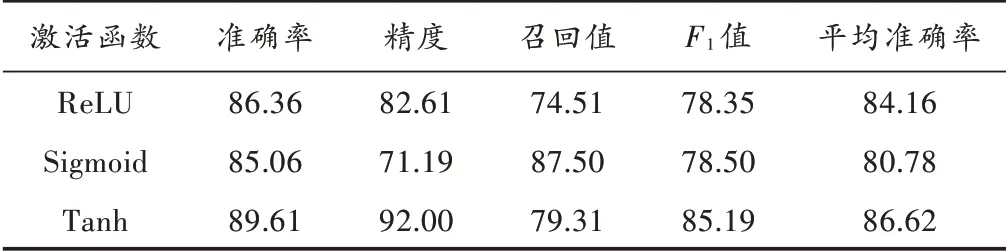
表2 三种激活函数的性能 %

根据表2 数据，容易得到Tanh 的性能最佳。原因在于Tanh 是以零为中心的函数，其表达式为：

输出值在[-1，1]之间，这使得经Tanh函数运算后不会出现zigzag 现象。Tanh 还具有放大特征之间差异性的特点，能够提高模型预测性能。Sigmoid函数的表达式为：

其函数值全为正数，输出值在[0，1]之间，数据流经激活层后进行反向传播时会出现参数同号的问题，容易造成优化路径出现zigzag 现象，减缓了模型的收敛速度。ReLU 函数的表达式为()=max(0,)，其优点是解决了在＞0 方向的梯度消失问题，运算时只需判断参数是否大于0，加快了模型收敛速度。但ReLU 也不是以零为中心的，并且在参数小于0 时输出为0，从而可能会导致网络中某些神经元永远不会被激活。因此，根据对比结果，本文选用Tanh 作为模型的激活函数。

1.4 优化算法的选择

本文对比了常用的4 种神经网络模型优化算法：随机梯度下降（SGD）、自适应矩估计（Adam）、Adagrad 和Adadelta。

SGD 的求解思路是根据每一个样本x和标签y，得到更新参数：

由于SGD 会对每个样本计算梯度，导致算法会受到噪声数据的影响，即并不是每次迭代都朝着整体最优化方向，但算法优化方向是朝着全局最优解的，且最终结果也往往在全局最优解附近。Adagrad 的优化策略是让学习率适应参数，即对于少数的特征赋予其较大的学习率；对于多数的特征赋予其较小的学习率。其缺点是由于不断地累加梯度的平方，导致学习率可能会变得无限小。Adadelta 算法是Adagrad 算法的扩展，通过添加一个特定大小的历史梯度计算窗口，来处理Adagrad 学习率持续变小的问题。Adam 对参数计算自适应学习率，同时还保存了一个历史梯度的指数衰减均值m，Adam 可自动更新m来抵消由于不恰当的初始化带来的偏差。使用不同优化算法的模型性能见表3。

表3 使用不同优化算法时的模型性能 %

表3 的性能分析表明：优化算法Adam 的预测准确率高于其余优化算法0.65%～9.09%。因此，本文构建的深度残差网络选用Adam 作为优化算法。

2 在糖尿病预测中的应用

2.1 两类数据集的整理

本文采用UCI 机器学习库的公开糖尿病数据集，原数据集中共有768 条样本数据和9 个属性字段。其中，确诊为糖尿病的样本数为500 个，未确诊为糖尿病的样本数为268 个。样本类别呈现不对称状态。表4 统计了数据集中属性列的均值、方差、最小值、四分位数及最大值。根据表4 中的数据发现，葡萄糖、血压、皮肤厚度、胰岛素、BMI 属性中的最小值均为0，显然这是错误数据，需要对其进行处理，这是因为数据集中的噪声数据会导致模型性能降低，严重时可使模型无法收敛。将上述5 个特征按是否确诊糖尿病进行分类，对未确诊糖尿病且存在异常值的样本使用该类别所有样本的中位数填充，对确诊糖尿病且存在异常值的样本也进行同样处理，于是，得到一个原始数据集。

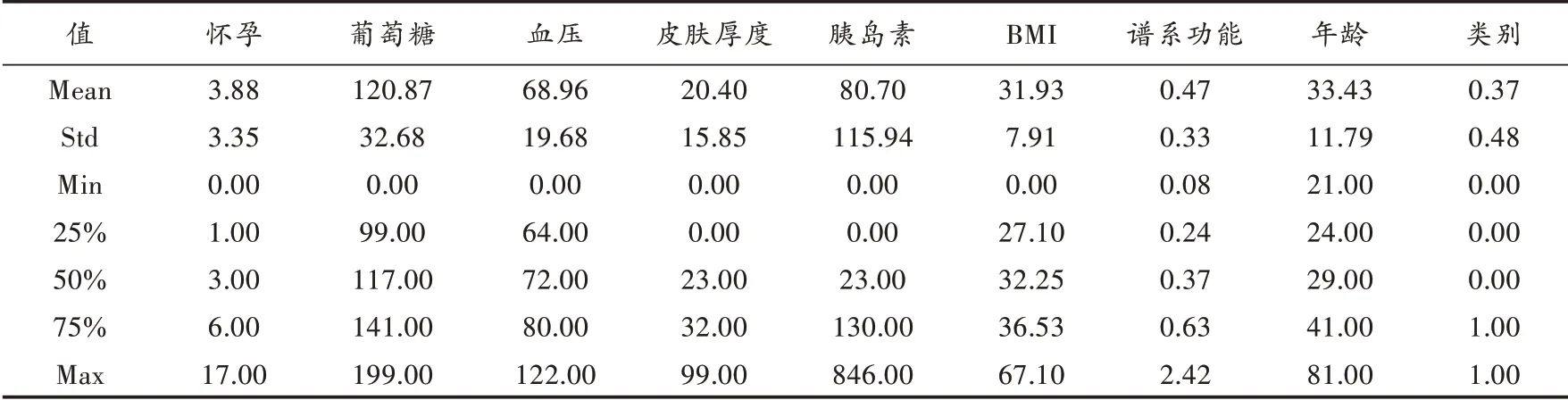
表4 数据集各属性统计值

同时，由于原数据集中确诊糖尿病样本数是未确诊的两倍，从确诊样本随机选取268 个样本，这样，便得到一个样本均衡数据集，其中的确诊糖尿病的样本数和未确诊糖尿病的样本数均为268 个。

2.2 特征选择

为选取最优特征，提高模型预测准确率，本文使用梯度提升树算法对原数据集中的特征计算其重要性得分。梯度提升树的基本思想是生成多个决策树，每个决策树用来拟合之前累加模型损失函数的负梯度，使累加模型的损失在负梯度方向减少，直到生成一个强学习器。梯度提升树模型表示为

式中：为决策树的数量；θ是第个决策树的参数；h(;θ)表示第个决策树。使用前向分布算法，第步提升树模型更新为：

更新过程中，θ要使得第步提升树f()累加到的损失函数最小化，即：

通过这个思想计算每个特征在分类时所占的比重，以此得出每个特征的重要性程度。表5 只截取了得分最高的前4 个特征，其余特征的重要性得分均在0.1以下。

表5 特征重要性得分

3 预测结果对比分析

3.1 有无使用深度残差网络的对比

为检验深度残差网络用于糖尿病预测的可靠性，比较了具有相同数量的参数、深度、宽度和计算成本的普通神经网络与深度残差网络。在分别进行了5 次训练后，图5 中数据显示，深度残差网络的性能明显高于无残差结构的神经网络。具体地，深度残差网络比无残差结构的准确率提高了2.6%，精度提高了6.55%，值提高了2.73%，平均准确率提高了2.59%。实验结果证明了深度残差网络可用于糖尿病预测且具有良好性能。

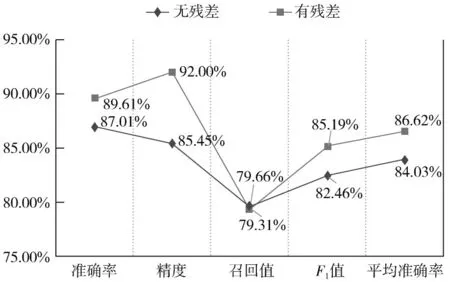
图5 有/无残差的模型性能比较

3.2 基于原始数据集的模型预测性能

对于原始非均衡数据集，对深度残差网络与随机森林模型、朴素贝叶斯模型、决策树模型、支持向量机模型、逻辑回归模型在准确率、精度、召回值、值和平均准确率上进行对比分析。其中，深度残差网络模型的最优参数为：优化算法Adam、损失函数Binary_corssentropy、验证集比例为训练数据的30%、激活函数Tanh、Epochs 为100。支持向量机模型的最优参数有：惩罚参数为10、核函数为RBF；而决策树算法中的3 个主要参数的最优参数选值为：max_depth=9，min_impurity_split=0.27，min_samples_leaf=9。

采用上述参数后，利用此6 种预测模型对原始数据集均进行了10 次实验，实验结果见表6。数据显示，深度残差网络模型获得最高准确率为89.61%，值最高为85.19%，模型预测性能较朴素贝叶斯算法提高了近12%。相比于随机森林算法，准确率提升了1.95%，精度提升了9.65%。综合来看，深度残差网络的平均预测准确率高于其他5 种机器学习算法的平均准确率。另外，在10 次训练任务中，深度残差网络模型的预测准确率没有出现大幅波动，说明在使用原数据集进行糖尿病预测时，深度残差网络优于5 种经优化的机器学习算法。

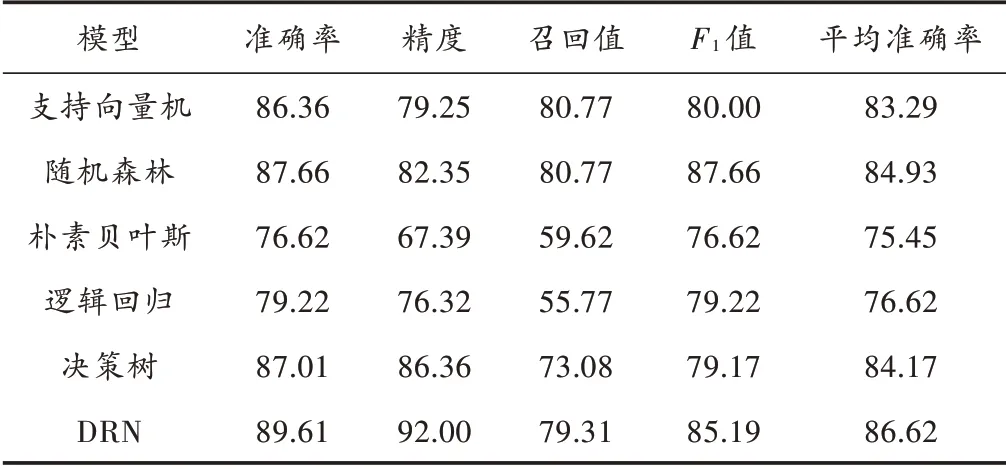
表6 原始数据集6 种预测模型的性能 %

3.3 基于样本均衡数据集的模型预测性能

采用3.2 节中各算法的最优参数，对样本均衡数据集进行了10 次实验，各模型性能数据如表7 所示。

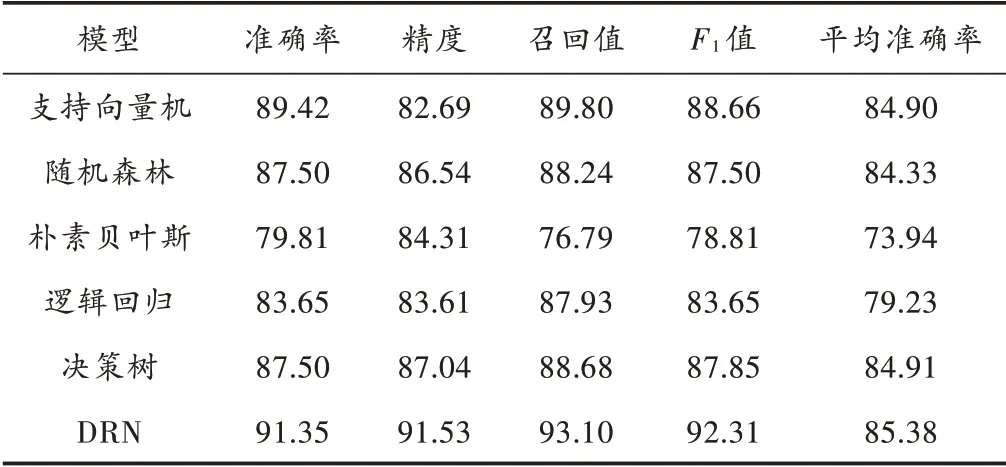
表7 样本均衡数据集6 种预测模型的性能 %

表7 的结果显示：深度残差网络模型获得最高准确率为91.35%，值最高为92.31%，预测性能较原始数据集的结果分别提高了1.74%，7.12%。同时，其余5 种模型性能评估指标较原始数据集的结果均稳中有升。但总的来看，深度残差网络的平均预测准确率还是高于其他5 种机器学习算法的平均准确率。

值得一提的是，使用样本均衡数据集时，深度残差网络模型的预测性能出现略微下降，平均准确率下降了1.24%。这是由于样本数量较少，模型无法学习到整体的数据特征，模型参数无法得到有效更新，致使模型预测性能出现下降。

4 结 论

本文构建了深度残差网络模型，并基于UCI 糖尿病数据集，将深度残差网络与支持向量机算法、决策树算法、随机森林、朴素贝叶斯、逻辑回归等模型进行了预测性能对比分析。结果表明，深度残差网络模型对原始数据集及构造的样本均衡数据集的预测性能都是最优的。但在减少样本量后，深度残差网络模型的性能出现下降，同时网络训练过程中损失值出现波动。实验结果表明，尽管使用深度残差网络可以解决神经网络退化问题，加快网络收敛速度，但是模型仍需要大量的样本输入，以获得更高的精确率。