基于时间序列神经网络的温度场预测分析

姚兆明，彭上海

(安徽理工大学 土木建筑学院,安徽 淮南 232001)

人工冻结法在隧道掘进、矿井与地铁建设等领域有着广泛的应用，施工过程中的冻胀融沉现象会影响工程施工安全和周围环境，冻胀融沉病害与土体水分迁移和温度场的变化有关。对温度场进行监测和预测，根据温度变化可以及时有效地提出防范措施，因此研究冻结过程中温度场的分布变化对人工冻结法施工有指导意义。影响人工冻土温度场的变化有诸多因素，目前温度场预测方法在建立模型时还不能较为全面地考虑影响人工冻土的温度场参数，进而不能较为精确地进行预测。

在室内冻胀试验温度场温度实测样本的基础上，利用人工神经网络对样本进行处理，通过建立基于时间序列的BP神经网络模型,使用计算机软件进行学习和训练并运用该网络结构来预测未知的温度场。姚兆明等[1]提出一种基于支持向量机的人工冻土温度场的预测模型，为温度场的预测提供一个新方法。魏胜田[2]对信湖煤矿井冻结壁的温度场进行时间序列预测分析，较精确地找出温度变化的内在规律。姚兆明等[3]提出一种神经网络结合遗传算法的动态网络结构，对冻结法施工井筒温度场进行预测，并与实测数据进行比较，表明该方法能够较好地预测未知温度场。

目前在岩土工程领域的智能预测方法主要有神经网络、支持向量机、遗传算法等。本文主要采用BP神经网络对冻结过程中温度场进行预测。BP神经网络是由Rumelhart和Mccelland为首的科学家小组提出的一种神经网络模型，该网络模型算法成熟，应用广泛。吴财芳等[4]基于时间序列BP神经网络对未来7 d的煤层气井产能进行预测，实现对煤层气井产能的人工控制。李哲等[5]构建了基于6种因素影响下煤炭价格预测的BP神经网络模型，可以较好地对未来一段时间的煤炭价格进行预测，并给出了相关的政策建议。赵琥等[6]通过建立深水钻井作业井下温度场的预测模型，与现场实测温度进行对比验证了模型的正确性。Shi Yin Zhang等[7]通过建立人工冻土温度的支持向量机计算模型，利用不同核函数的支持向量机对人工冻土冻结温度计算进行分析，确定适合人工冻土冻结温度计算的核函数，结果表明该方法是一种有效的方法。

在冻结温度场分析过程中，实测温度本身构成了时间序列，本文基于神经网络，用时间因素建立了温度场的变化模型，期望根据时间序列可以较为准确地找出冻胀过程中温度场变化的内在规律。

1 试验方案

1.1 土样的物理特性

本试验所用的泥炭土取自西南某地区，土样呈黑褐色,具体物性参数见表1。

表1 细粒土的物性参数

1.2 试验装置

根据试验研究内容及《土工试验规程》的相关要求，采用高低温试验机开展试验。该试验装置主要包括恒温试验箱体，水分监测系统，温度监测系统，位移监测系统，底板制冷及低温恒温液循环系统。试验中水分场监测系统采用DS18B20温度传感器，温度场监测系统采用DS18B20温度传感器以及配套的STA-DDS18B20数据采集模块，并利用采集软件实时读取和记录试样不同位置的数据。整体结构示意图如图1所示。

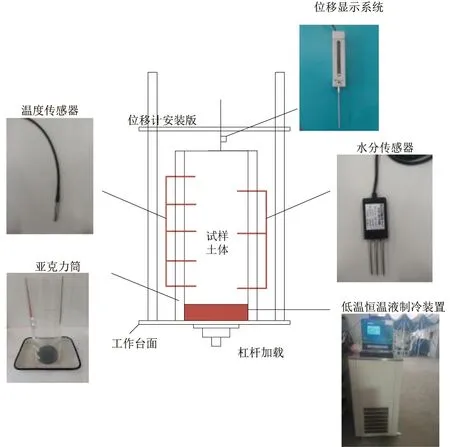
图1 冻胀试验装置结构示意图

1.3 试验方法

严格按照《土样和试样制备》土工试验规程的要求配制试样。试样底端冻结温度分别设置为-10 ℃、-20 ℃、-25 ℃ 3个等级，外部设置为恒温5 ℃。在封闭不补水系统下进行冻结试验并监测泥炭土的位移场、水分场、温度场的分布。为保证温度、水分等数据采集的正常进行[10]，对试验步骤和方法作出要求。

步骤1：将现场取回的试验土样烘干碾碎后过2 mm筛，按照试验要求配制含水率为60%的土样，用保鲜膜密封包装24 h静置养护，确保土体中的水分均匀分布。

步骤2：试样尺寸为高150 mm，直径60 mm的圆柱体；填筑前在筒壁内侧均匀涂抹凡士林以减少土样和筒壁内侧间的摩擦力，在试样顶部覆盖一层塑料膜进行密封处理；采用压样法将配制好的土样分为3层填筑到亚克力材料制作的试样筒内，分层击实。

步骤3：启动低温恒温液循环系统，为保证试验过程中外部处于恒温状态，在试样筒外包裹一层3 cm厚的保温材料；将温度传感器、水分传感器按照试验要求插入试样，在土体上方安装位移计，并将位移计测量端头与土体上方板相接触，试验过程中对温度数据、水分数据、位移数据进行实时监测和记录；以土体上端界面为零界面，试验中温度传感器分别置于-25 mm、-50 mm、-75 mm、-100 mm、-125 mm处，水分传感器分别置于-40 mm、-80 mm、-120 mm处。

步骤4：持续冻结50 h后，位移场、水分场、温度场趋于稳定，分别保存温度、位移等数据，停止试验。

2 试验结果分析

2.1 温度场分析

图2为各试样在不同测点温度随时间变化关系图。

(a)试样-冷端温度-10 ℃ (b)试样-冷端温度-20 ℃ (c)试样-冷端温度-25 ℃

由图2可知：试样初期阶段降温较快，随后进入缓慢降温的状态，经过一段时间之后温度场趋于稳定；可以将试样的整体温度变化曲线分为3个阶段：快速降温阶段(0～10 h)、缓慢降温阶段(10 ～30 h)、温度稳定阶段(30～50 h)；冷端温度是冻结的根源，距离冷端越近，土体温度下降速率越快[7]；冷端温度越低，冻结过程中温度场越低，即土的平均温度越低。冷端温度分别为-10 ℃、-20 ℃、-25 ℃时，3个试样试验结束后各测点稳定温度见表2。

表2 不同冷端温度试样各测点稳定温度值

2.2 水分场分析

试验过程中对土体水分进行实时监测，3个不同冷端温度下含水率沿试样高度方向分布情况如图3所示。由图3可知：在-120 mm处3组试验的规律相似，都是在开始阶段快速下降，且趋于稳定时含水率较低；距离冷端越近，在温度梯度的作用下，土体中水分快速冻结，所测含水率越低；在-40～-80 mm范围内，由于土体中气态水、液态水不断向冻结锋面迁移，从而导致冻结锋面以上未冻结区的含水率低于初始含水率；冷端温度越低，测得趋于稳定状态的含水率越低。

(a)试样-冷端温度-10 ℃ (b)试样-冷端温度-20 ℃ (c)试样-冷端温度-25 ℃

3 水热耦合下冻结温度智能方法预测

3.1 时间序列神经网络

时间序列是将某种统计指标的数值按一定的时间顺序排列成形的数列。该预测基于统计学方法，分析和编制出符合数据变化规律的函数，再根据所反映的发展过程和趋势，进行延伸以预测未来某一段时间的数值，从而解决实际问题。在冻结温度场分析中，实时温度本身构成了时间序列[7]。本文基于神经网络，考虑时间因素建立温度场变化模型。

3.2 时间序列神经网络预测模型的建立

在冻结试验过程中，采用5个温度传感器分别插入距离顶端零界面25 mm、50 mm、75 mm、100 mm、125 mm的5处。温度监测系统性能稳定，选取2021年3月16日至18日共40 h的监测数据为时间序列分析对象。选前30 h共30组监测数据作为训练样本。

时间序列神经网络的预测本质上是对已知样本数据进行训练，即利用神经网络具有自适应联想记忆的能力去逼近一个函数[11]。设一组时间序列为X(t)，t=1，2，……，N。使用前t个点的数据来预测第t+1个点的数据，则该预测模型的输入向量是前t个点，输出向量则是t+1个点的数据。对于时间序列X(t)，t=1,2，……N，则可生成N-t个样本[6]。样本集构造如表3所示。

表3 时间序列神经网络样本构造方法

3.3 神经网络结构参数的设置

通过数据可直接确定建立基于时间序列的动态神经网络模型的输入层节点数量和输出层节点数量。为提高精度，首先将数据进行归一化处理，在预测时，隐含层的数量会影响模型预测的精度。为防止节点过多导致过度拟合或节点过少导致拟合不足，根据相关经验公式，使用试凑法确定隐含层的节点数。比较不同隐含层节点的预测结果误差，确定隐含层个数以保证模型的准确性。其计算公式为：

(1)

其中：y为隐含层节点合数；m和n分别为输入层、输出层节点个数；p为1到10之间的常数。

通过试凑法可得，当隐含层节点数为5时，预测模型的效果最好。隐含层神经元的转换函数采用S型正切函数tansing，输出层神经元的转换函数purelin，取误差指标10-8。训练函数选取trainlm的BP网络，最大训练循环次数为1 000。

3.4 模型评价指标的选取

为评价该神经网络模型的预测性能，采用平均绝对误差(EMA)和均方根误差(ERMS)来评价时间序列神经网络预测模型的预测结果。两种指标分别定义为：

(2)

(3)

4 结果分析

对冻结试验过程中底端温度为-10 ℃时的温度场进行预测。以0～30 h的温度场实测数据为训练数据，采用时间序列BP神经网络模型预测31～40 h的温度场，并将预测值与实际值进行对比，并对相对误差进行分析，结果如图4所示。

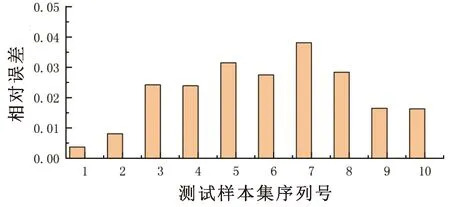
图4 温度场预测值与期望值相对误差示意图

由图4可知：时间序列神经网络预测模型的预测值与实际值的相对误差较小，平均值为0.045 8。为了更为全面地检验模型的精确度，将31～40 h的温度场实际值与预测值进行对比见表4，从表4分析可得二者较为接近，将表4的实际值与预测值代入性能指标公式中，可分析计算得出BP模型的ERMS的值为3.47%，EMA的值为6.68%，表明时间序列神经网络预测模型的准确性和可靠性。

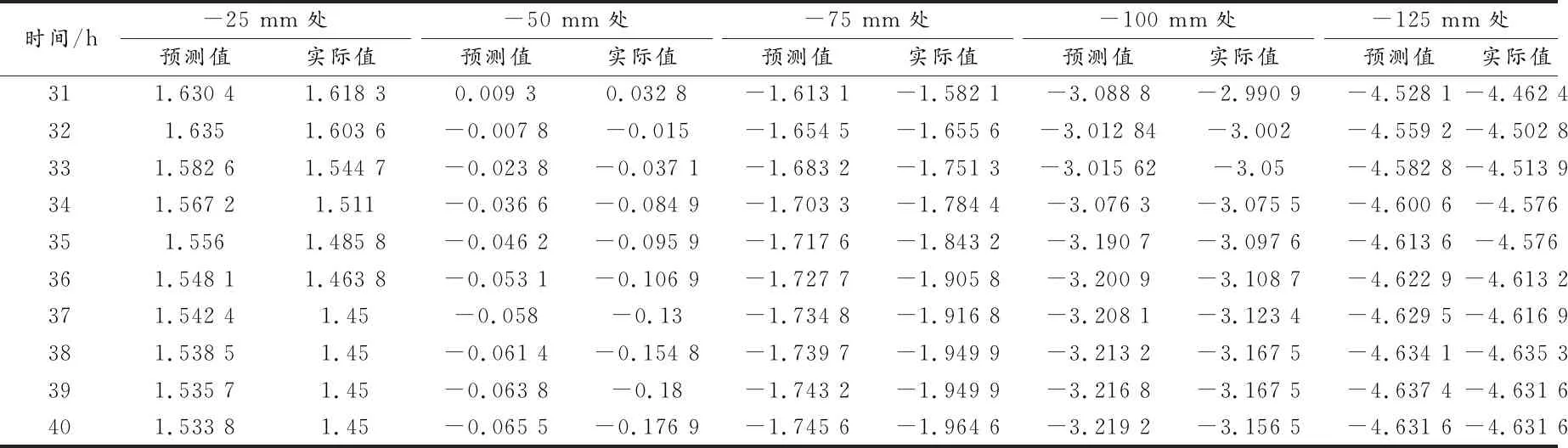
表4 预测温度与实际温度对比 ℃

5 结论

(1)冻结温度场整体温度变化分为快速降温阶段、缓慢降温阶段、稳定阶段；且距离冷端越近，温度下降越快，冷端温度越低，稳定阶段的含水率就越低；冻胀量发展越迅速，冻胀量累计增长越明显。

(2)采用时间序列神经网络预测模型预测的温度场接近实际值，其评价指标均方根误差和平均绝对误差均很小，预测精度符合预期，模型合理；可以有效地短期预测人工冻结温度场随时间的变化趋势，神经网络预测方法对冻结法的工程应用具有实际参考意义。