基于准北东地系地面静态对准算法

王献忠 张 肖

1.上海航天技术研究院，上海 201109；2.上海航天控制技术研究所，上海 201109；3.空间智能控制技术重点实验室，上海 201109

0 引言

地面运载和武器系统发射前需要进行初始对准，一般基于捷联惯组测量的本体系下地球自转角速率和重力加速度确定飞行器初始姿态。

国内外学者对捷联惯导初始对准进行了广泛的研究，文献[1]通过将无迹卡尔曼滤波算法(UKF)和鲁棒环节引入到粒子滤波(PF)的重要性密度函数中，得到了RUPF 算法，提高了算法的鲁棒性。文献[2]采用改进的UKF算法进行捷联惯导初始对准研究，减少了UT变换中Sigma点的计算数量，提高了运算效率。文献[3]基于四元数自适应卡尔曼滤波进行捷联惯导初始对准研究，直接以初始对准时刻的四元数作为估计状态，建立卡尔曼滤波模型，同时通过对观测模型中的观测矩阵进行改造，有效加快了算法的收敛速度。文献[4]利用以惯性系为参考基准的解析对准法和卡尔曼滤波精对准方法，对高精度全自主对准技术和其在运载火箭上的应用展开了详细论述。综上述文献，对于静态对准算法的研究，目前的研究重点在于提高对准的精度、算法的鲁棒性及收敛速度。文献[5]针对微惯组测量噪声大，不能辨别地球自转角速度，造成捷联惯性导航系统不能实现自对准的问题，采用GPS辅助微惯组进行初始对准。针对大失准角初始对准问题，文献[6]在游动方位角坐标系下建立了方位大失准角条件下的SINS初始对准误差模型；文献[7]基于二阶非线性量测方程的二阶泰勒级数展开的滤波算法进行捷联惯导大失准角初始对准研究。受启发于上述文献，本文针对利用本身测量精度并不是很高的陀螺如何实现高精度初始对准，及适应任意姿态和无初值条件下的初始对准和参数估计问题进行研究。

本文基于粗对准姿态建立准北东地系，通过准北东地系的建立使角度误差小且三轴近似解耦；估算准北东地系重力加速度和地球自转角速率，通过不断迭代修正，提高了角速度的测量精度；基于高精度的角速度测量信息，提出了一种易于工程实现的解析式精对准算法，在保证稳定收敛的前提下精度优于0.05°。

1 地面粗对准

1.1 计算重力加速度

基于对准点纬度和高度计算重力加速度：

(1)

其中：

g0=9.7803267714m/s2为地面标准重力加速度；k1=0.00193185138639和k2=0.00669437999013为重力加速度修正系数；B为地理纬度；Re为地球半径；h为对准点地面高度。

1.2 计算本体系重力加速度和地球自转角速率

基于加速度计输出的比力fs计算本体系比力fb：

(2)

其中：Αsb,a为加速度计在本体系安装矩阵。

基于陀螺输出的角速率ωs计算本体系地球自转角速率ωb：

(3)

其中：Αsb,g为陀螺在本体系安装矩阵。

1.3 计算本体相对北东地系粗对准姿态

北东地系如图1所示，在静态对准点基于重力加速度方向建立北东地(NED)坐标系，NED系加速度计比力如下：

(4)

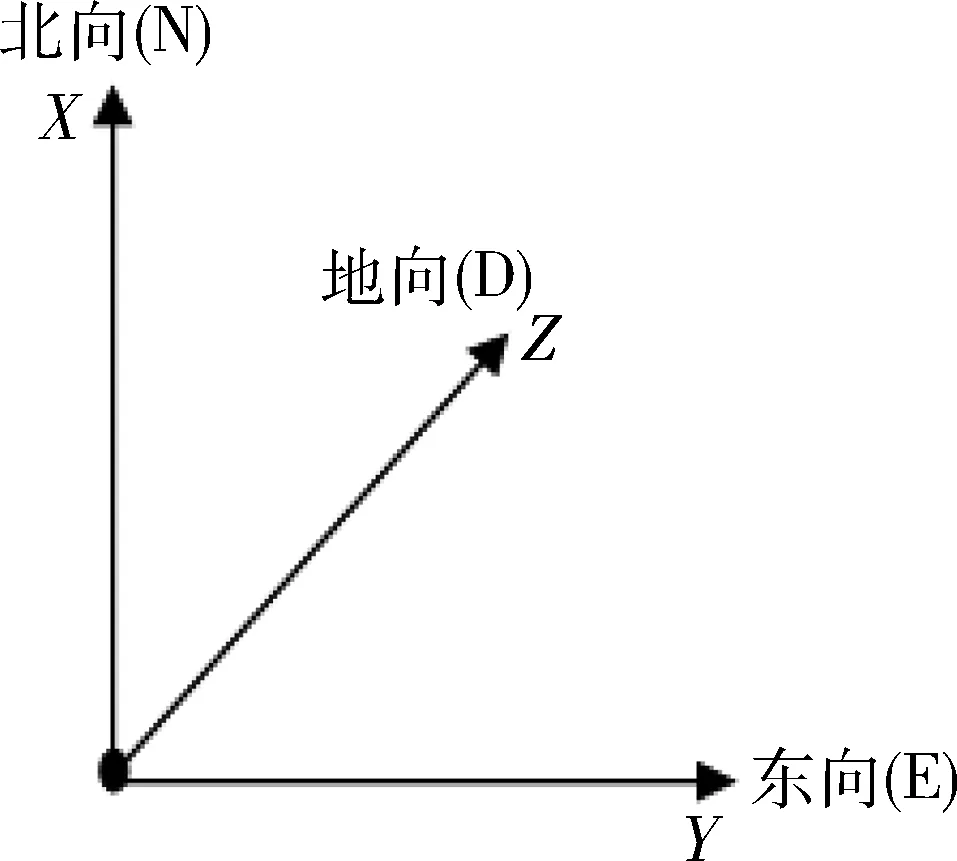
图1 北东地坐标系(NED)示意图

本体相对NED系3-2-1转序姿态转换阵Abn[7]：

(5)

其中：ψ为偏航姿态；θ为俯仰姿态；γ为滚动姿态。

(6)

求得：

(7)

(8)

(9)

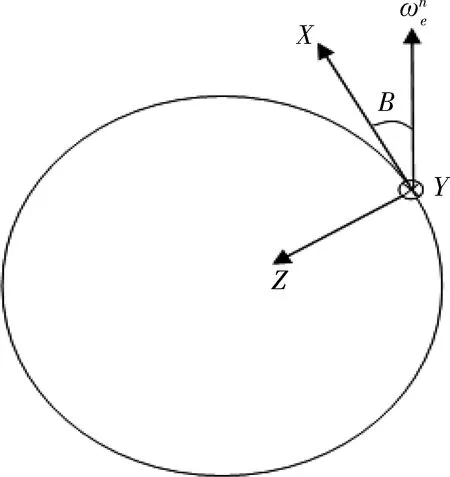
图2 北东地系地球自转角速度

(10)

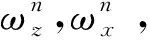
(11)

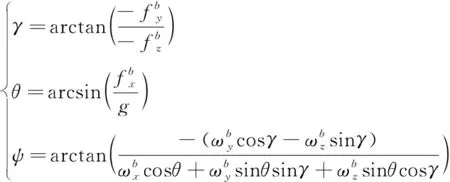
(12)

否则：

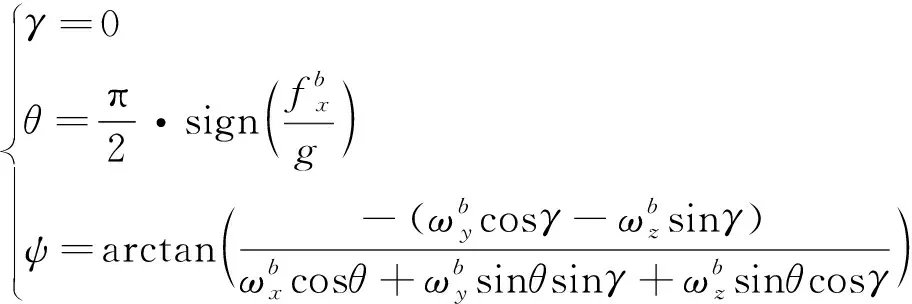
(13)

2 估算准北东地系重力加速度和地球自转角速率

2.1 本体系重力加速度和地球自转角速率转换到准北东地系

基于粗对准姿态建立准北东地系，将本体系比力fb转换到准北东地系：

(14)

其中：Αbn′为准北东地系到本体系转换矩阵。

将本体系地球自转角速率ωb转换到准北东地系：

(15)

其中：Αbn′为准北东地系到本体系转换矩阵。

2.2 准北东地系比力fn′和地球自转角速率ωn′滤波

准北东地系比力fn′和地球自转角速率ωn′滤波：

(16)

(17)

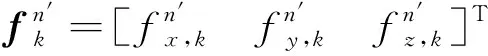
3 基于准北东地系精对准

3.1 估计水平失准角

基于准北东地系比力北向和东向分量估计水平失准角：

(18)

(19)

对水平失准角进行限幅处理，水平失准角大时比例作用强一些，加快收敛；水平失准角小时比例作用弱一些，避免振荡。

比例系数ka进行分段处理：

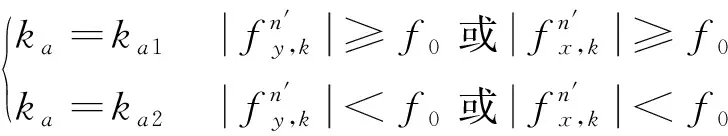
(20)

其中：ka1为水平失准角未收敛时比例系数，ka2为水平失准角收敛时比例系数，f0为比力水平方向分量判别阈值。

3.2 估计方位失准角

基于准北东地坐标系地球自转角速率东向分量估计方位失准角：

(21)

对方位失准角进行限幅处理，方位失准角大时比例作用强一些，加快收敛；方位失准角小时比例作用弱一些，避免振荡。

比例系数kω进行分段处理：

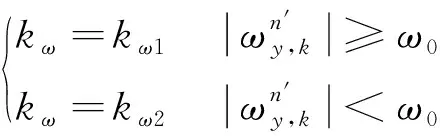
(22)

其中：kω1为方位失准角未收敛时比例系数，kω2为方位失准角收敛时比例系数，ω0为地球自转角速率东向分量判别阈值。

3.3 估计精对准姿态四元数

基于水平和方位姿态失准角估计精对准姿态误差四元数：

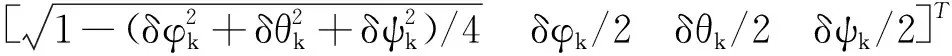
(23)

求得精对准姿态四元数：

qbn,k=δqk⊗qbn,k-1

(24)

qbn,0=qbn′

(25)

其中：qbn,k为第k步推算的本体系相对NED系姿态四元数，qbn,k-1为第k-1步推算的本体系相对NED系姿态四元数，qbn′为基于粗对准姿态确定的本体系相对NED系姿态四元数。

3.4 计算精对准姿态

令：

(26)

基于精对准姿态四元数qbn，求得Abnq[8]：

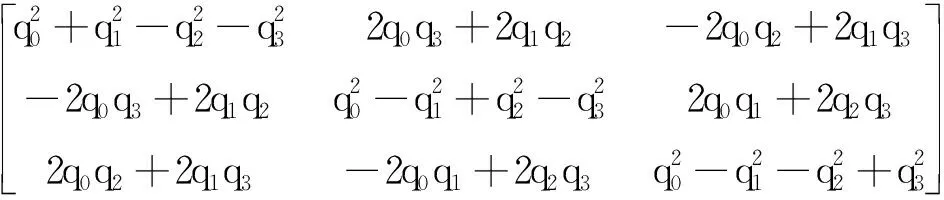
(27)

结合姿态按3-2-1转序求得Abn，按3-2-1转序求精对准姿态：

如果|a13|≤0.99999：

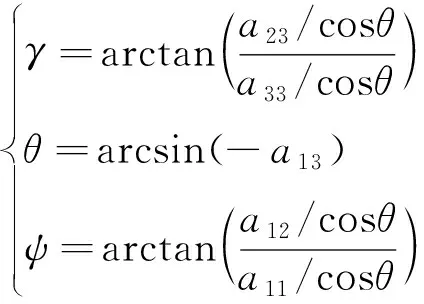
(28)

否则：

(29)

4 算法精度及收敛性仿真验证

4.1 算法精度仿真验证

地球表面静态对准点地固系经度121.2538°，纬度31.101985°，高度0m；3-2-1转序标称姿态ψ=41.5°，θ=-87.99°、φ=41.0°。

陀螺角速率常值漂移0.01(°)/h，随机漂移0.001(°)/h；加速度计比力常值漂移1×10-5g，加速度计加速度随机漂移1×10-6g。在粗对准基础上进行精对准，高精度惯组三轴姿态对准误差如图3所示，对准精度约0.04°。

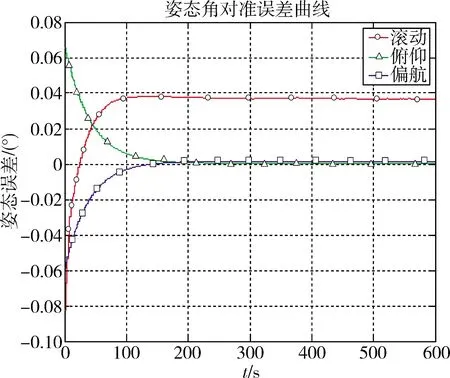
图3 高精度惯组三轴姿态对准误差曲线

陀螺角速率常值漂移0.1(°)/h，随机漂移0.01(°)/h；加速度计比力常值漂移1×10-4g，加速度计加速度随机漂移1×10-5g。在粗对准基础上进行精对准，一般惯组三轴姿态对准误差如图4所示，对准精度约0.4°。

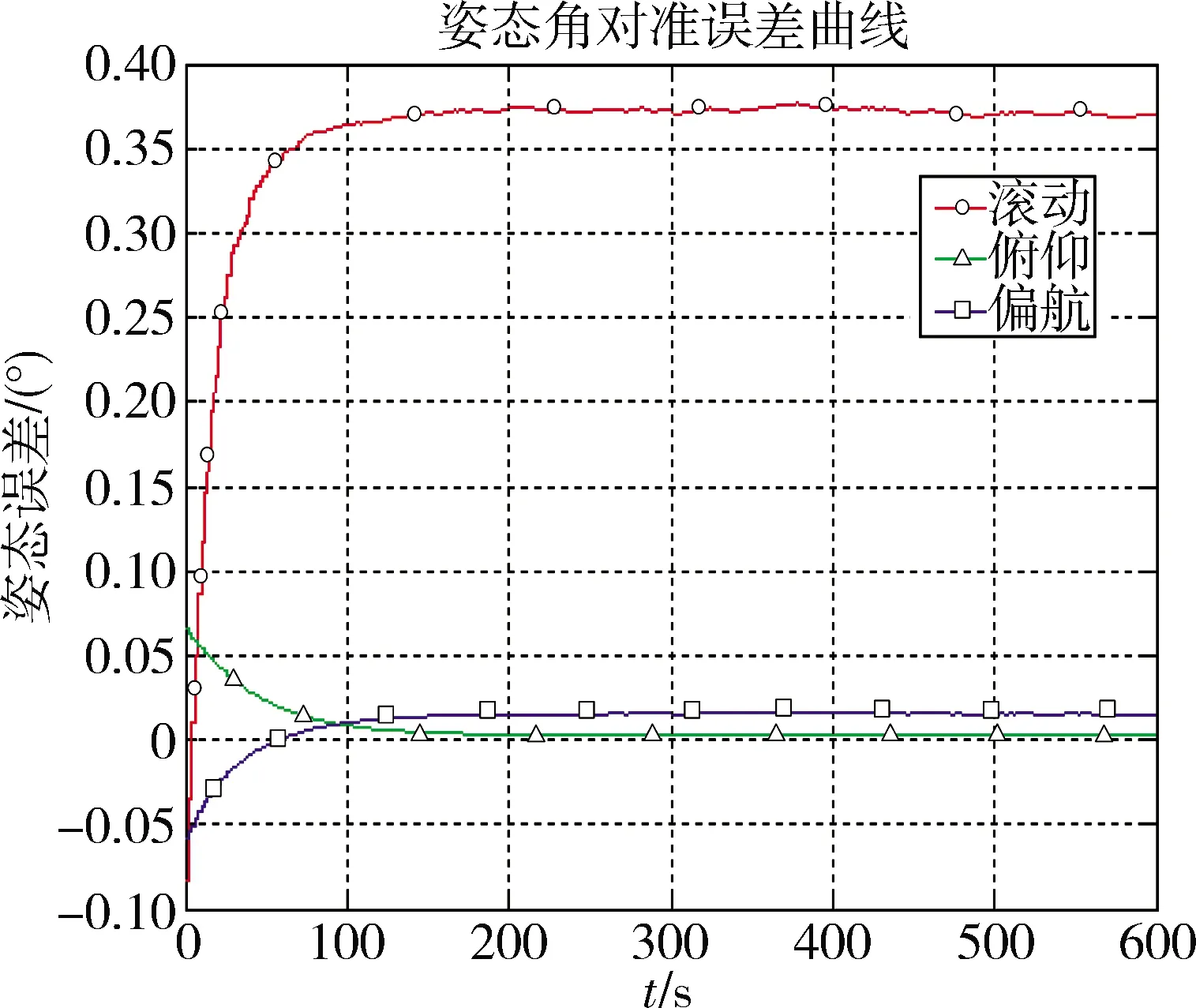
图4 一般惯组三轴姿态对准误差曲线

4.2 算法收敛性仿真验证

高精度惯组陀螺角速率常值漂移0.01(°)/h，随机漂移0.001(°)/h；加速度计比力常值漂移1×10-5g，加速度计加速度随机漂移1×10-6g。不估计粗对准姿态，设初始姿态ψ=0.0°；θ=0.0°；φ=0.0°，直接进行精对准，高精度惯组三轴姿态对准误差收敛后如图5所示，对准精度约0.04°。

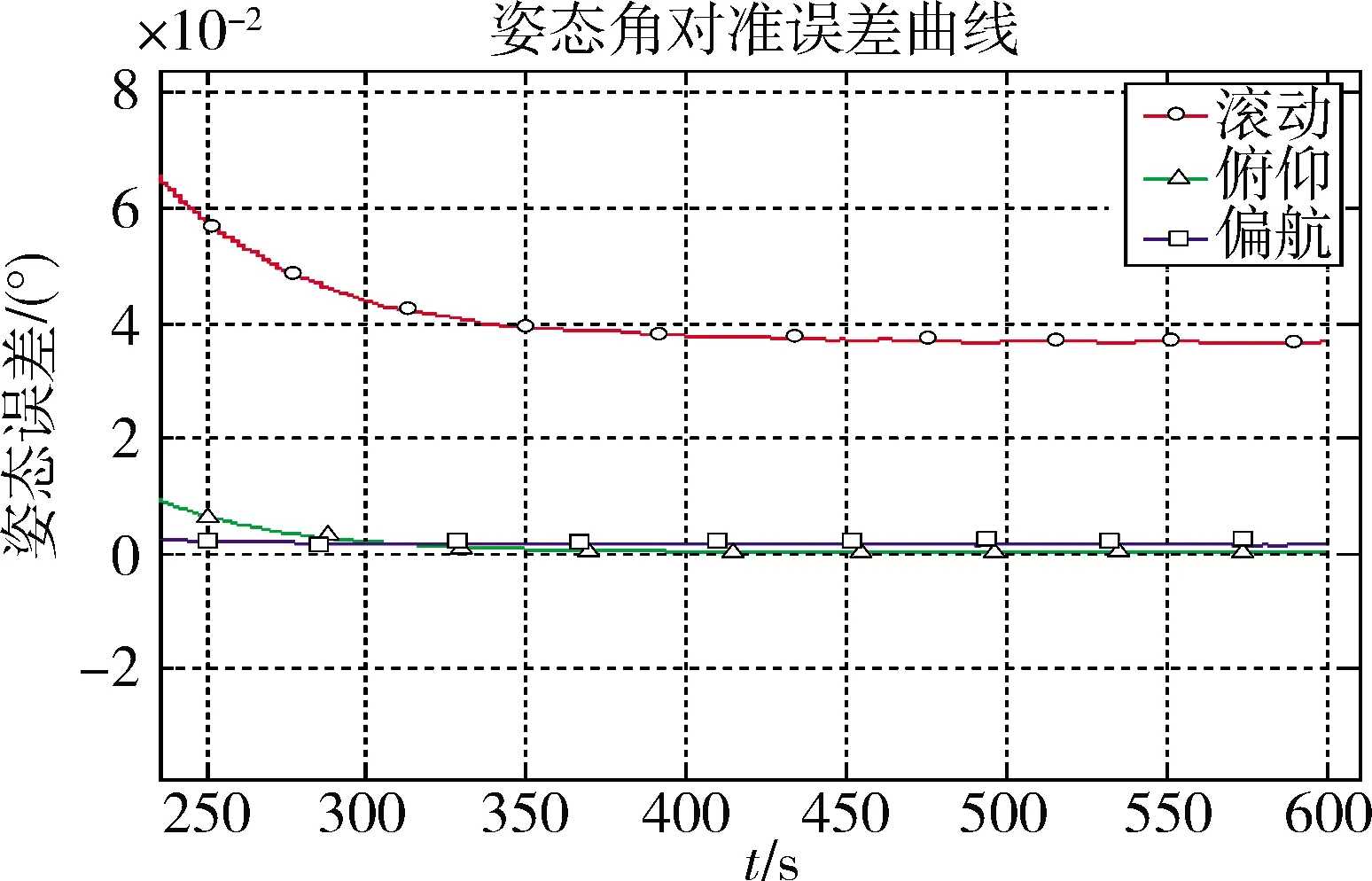
图5 高精度惯组直接精对准三轴姿态对准误差曲线

5 结束语

基于捷联惯组确定飞行器在地面相对北东地系姿态，通过准北东地系的建立使角度误差小且三轴近似解耦；通过不断迭代修正，提高了角速度的测量精度；进而基于高精度的角速度测量信息，提出了一种易于工程实现的解析式精对准算法。仿真验证了静态对准算法的有效性和收敛性。本文基于捷联惯组确定飞行器在地面初始姿态算法简单，易于工程实现。