一种基于速度-高度剖面的再入制导算法*

尤志鹏 邵 干 李 洋 杨 勇

中国运载火箭技术研究院，北京 100076

0 引言

空天飞行器再入过程具有约束多、大气及气动不确定性高等特点，设计精度高、自主性好、自适应性强的再入制导算法仍然充满挑战。航天飞机再入制导律是最早得到应用的升力式再入制导律，经过了多次飞行考验，从未发生致命性故障，被后续可重复使用飞行器(RLV)所继承并得到进一步发展[1-2]。此后，更加先进的再入制导算法得到广泛研究，自主性、快速性、适应性进一步增强[3-5]。

现有再入制导算法主要分为2类：标准轨迹制导和预测校正制导。目前，标准轨迹制导应用最广泛，Mease等[6-7]提出衍化加速度再入制导律(EAGLE)，比传统航天飞机再入制导律具有更强的自适应能力，可以应用于大横程再入。王鹏等[8]进一步考虑了基于阻力加速度-能量剖面再入制导算法的速度倾角控制问题，提升了制导精度和适应性。赵頔等[9]通过数值迭代确定满足终端约束的速度-高度剖面，制导精度较高。但是，标准轨迹跟踪制导算法需要离线设计标准剖面，自主性较差，不利于飞行器性能发挥。

预测校正制导通过比较预测终端条件与期望终端条件偏差形成制导指令，不需要事先规划飞行剖面。早期预测校正制导迭代参数较多，Fuhry等[10]通过解算倾斜角指令和倾斜角变号时机消除预测落点与期望落点偏差，但该算法计算复杂，计算资源消耗多。为降低迭代复杂度，Lu等[11]将攻角剖面固定，每制导周期仅迭代获取满足航程要求的倾侧角剖面，并通过倾侧角反号控制横程，得到一种通用预测校正制导算法[12-13]。刘刚等[14]进一步考虑了预测校正制导律设计过程中的攻角调节问题，增强了算法适应性。但是，上述制导算法在每个制导周期均需要在纵向运动平面内执行多次弹道积分，算法效率仍存在较大提升空间。

为降低预测校正制导计算复杂度，本文提出一种基于速度-高度剖面的预测校正再入制导算法。在每个制导周期通过卡尔曼滤波估计速度中点对应的无量纲高度，预测满足航程要求的速度-高度剖面，避免传统数值预测校正的多次数值迭代。同时，针对算法在再入飞行末端拟合系数奇异问题，通过切换为标准轨迹制导予以避免。

1 运动方程及约束

1.1 运动方程

假设地球是均质圆球，三维质点再入运动无量纲方程为：

(1)

L=ρ(VcV)2SrefCL/(2mg0)

(2)

D=ρ(VcV)2SrefCD/(2mg0)

(3)

式中:ρ表示大气密度；Sref,m分别表示参考面积和飞行器质量；CL,CD分别表示升力系数和阻力系数，与攻角α有关，而攻角通常按速度进行装订。

1.2 再入约束

再入过程约束主要包括动压约束、热流约束、过载约束、平衡滑翔约束，分别通过下式计算：

(4)

(5)

n=|Lcosα+Dsinα|≤nmax

(6)

(7)

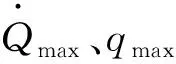
(8)

(9)

(10)

通过牛顿迭代求解式(7)，得到该约束下r和V的对应关系，至此，给定攻角剖面后，即可以得到再入走廊。

末端约束主要包含末端高度、末端速度、末端经纬度约束，对于基于速度-高度设计的飞行剖面，速度是自变量，因此高度约束和经纬度约束是末端主要约束。表达如下

r(Vf)=rf

(11)

θ(Vf)=θf

(12)

φ(Vf)=φf

(13)

式中：rf、θf和φf分别表示末端飞行器质心至地心距离、末端经度和末端纬度。

2 制导算法设计

飞行器再入段包括初始再入段和拟平衡滑翔再入阶。初始再入段气动力作用较弱，通常在满足航程、热流等约束作用下，以固定倾角飞行。当飞行器再入轨迹进入再入走廊并满足拟平衡滑翔条件时，飞行器进入拟平衡滑翔阶段，该阶段飞行时间长、飞行距离远、状态变化大，是再入制导律主要起作用阶段，本文从该段开始设计再入制导律。由于进入该阶段后，飞行速度随飞行时间逐渐降低，具有良好的单调性，因此可将速度作为运动方程的自变量，实现运动方程降阶，提高预测校正制导计算效率。

2.1 速度-高度飞行剖面拟合

再入飞行过程中，飞行器除需要满足再入走廊约束外，纵向轨迹还需要满足航程、终端速度和终端高度约束，除此之外，为保证飞行轨迹平滑，可进一步引入终端高度对终端速度的导数约束。飞行器当前纵向轨迹状态包含当前速度、当前高度、当前航迹倾角。由于

(14)

式中：h表示无量纲飞行高度，因此

(15)

即航迹倾角约束可转化为飞行高度对飞行速度的导数约束。因此可利用三次分段多项式形式的速度-高度飞行剖面拟合纵向飞行剖面，即

(16)

式中：aj,bj,j=0,…,3是拟合系数，Vm表示当前速度至交班点速度的速度中点，即Vm=(Vi+Vf)/2，在第i个制导周期，已知状态主要包括当前点的速度Vi、高度hi、航迹倾角γi，再入段交班点的速度Vf、高度hf。初始及终端状态构成四组约束，即(Vi,hi)、(Vi,(dh/dV)i)、(Vf,hf)、(Vf,(dh/dV)f)。此外为满足连续性要求，需要两个分段在Vm处飞行高度相等且高度相对于速度的导数及二阶导数相等，形成三组约束。同时，航程要求可通过调整Vm处飞行高度hm实现，至此形成了8组约束，可对拟合系数进行求解。在速度-高度剖面内航程随速度变化表达为：

(17)

将式(15)代入，可得飞行航程与期望待飞航程之差可以表示为

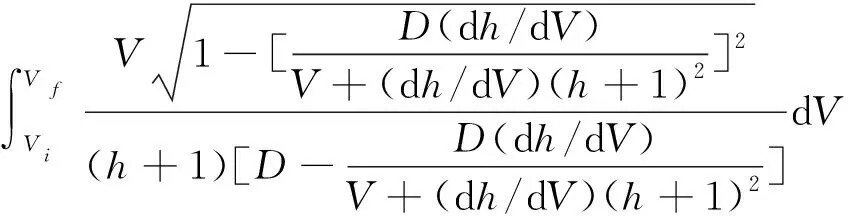
(18)

式中：Rexp表示期望待飞航程。

选择合适的hm，使得S(hm)=0，从而满足航程约束。

2.2 纵向制导指令

为得到期望的纵向航程，需要在每个制导周期获得合适的hm，从而确定飞行剖面并得到倾侧角幅值。

通过卡尔曼滤波对每个制导周期内满足式(18)的hm进行辨识，利用辨识结果求解拟合剖面的拟合系数，进而产生该制导周期所需要的制导指令，避免了传统数值预测算法需要多次积分纵向运动方程的不足，增强了算法实时性。

建模过程如下：

状态方程：

hm_i+1=hm_i+εi

(19)

观测方程：

Zi=S(hm_i)+νi

(20)

式中：i表示第i个制导周期，hm_i+1,hm_i表示第i+1和第i个制导周期速度中点对应的无量纲飞行高度；εi及νi为互不相关零均值高斯白噪声，其协方差分别记为Qi,Wi。

为获得使再入剖面满足航程约束的hm_i，可将观测值设置为Zi+1≡0。hm_i必须满足再入走廊约束并且具有一定的裕度，将速度中点对应飞行高度距离再入走廊边界的无量纲距离取为不小于κ=5×10-4，修正后的辨识结果见式(21)。

(21)

观测方程是非线性的，滤波过程中需要通过式(22)所示的差分计算观测矩阵Hi+1。

(22)

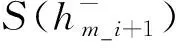
在每个制导周期，当hm_i确定后，可通过式(23)求解该制导周期对应的速度-高度剖面拟合系数。

(23)

为获得倾侧角指令，将飞行高度对速度求二阶导数，得

(24)

其中

(25)

(26)

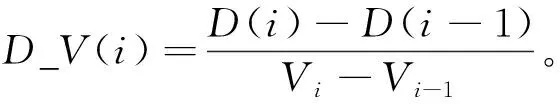
(27)

当前飞行状态接近终端状态时，式(23)求逆过程会出现奇异。为解决该问题，当前飞行速度与终端速度之差小于100m/s时，停止预测校正制导，不再更新飞行剖面，改为跟踪最后一次产生的飞行剖面，即式(28)。

cosσ=

(28)

式中：ξ,ω分别是阻尼比和自然频率，可取为固定值；href为参考轨迹对应的高度。为进一步增强跟踪能力，考虑引入倾侧角反馈，即

Lcosσ′=Lcosσ-K(γ-γref)

(29)

式中：K是反馈系数；γref为参考剖面对应的航迹倾角。

2.3 横向制导

横向制导采用基于航迹偏角偏差走廊的倾侧角反转实现，表达如下

(30)

式中：Δψup和Δψdown表示航迹偏角走廊上边界和下边界；Δψ表示航迹偏角偏差，计算如下

Δψ=ψ-ψLOS

(31)

ψLOS即当前位置至目标点的理想视线角，计算如下

(32)

至此完成算法设计，流程见图1。

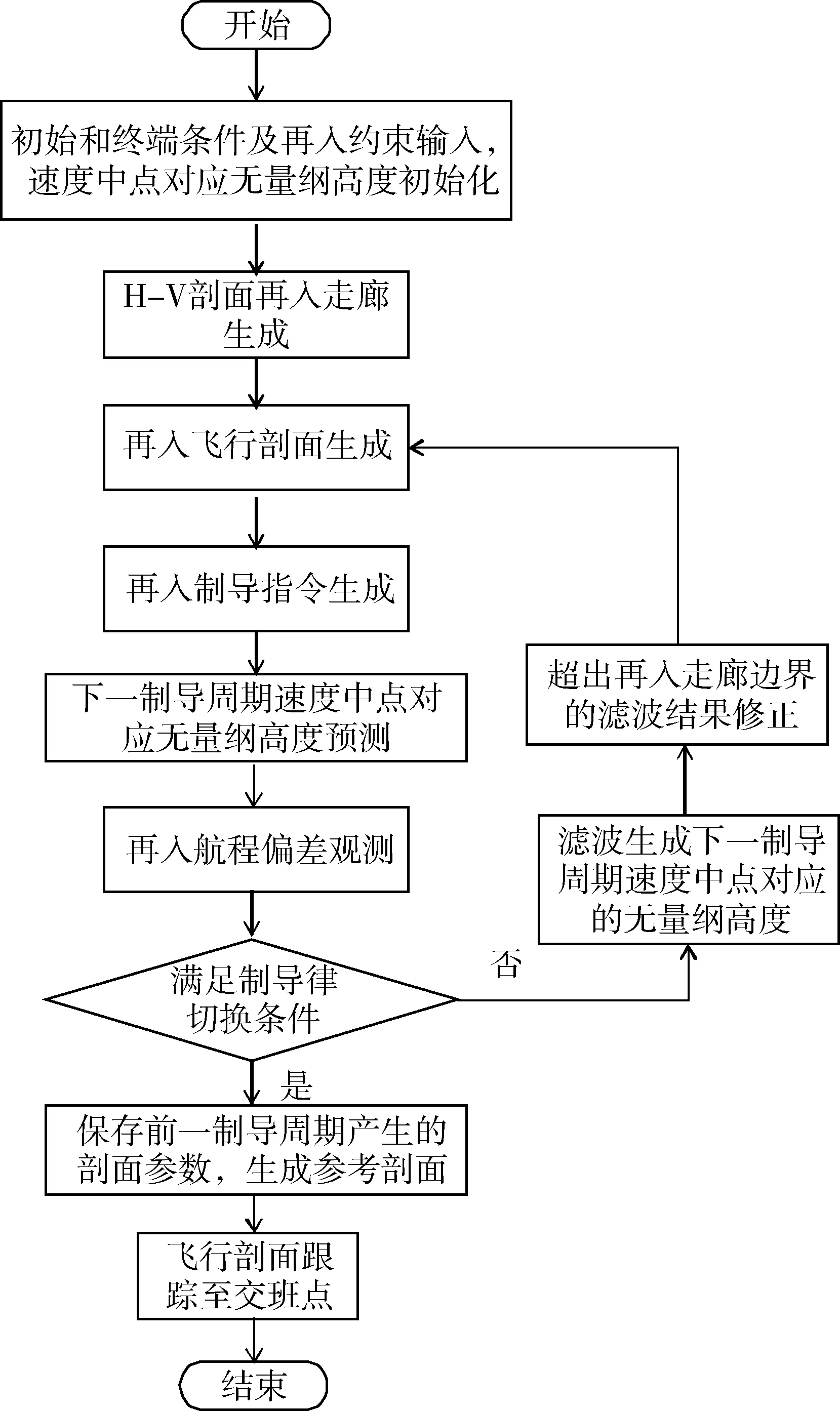
图1 算法流程

3 仿真校验

仿真模型参考文献[12]，攻角剖面取为

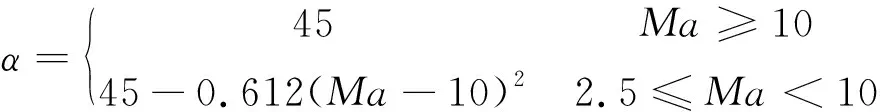
(33)

3.1 标称状态仿真

对4种不同航程下的算例进行仿真验证。它们初始再入位置不同，交班点高度为25km，初始状态如表1所示。

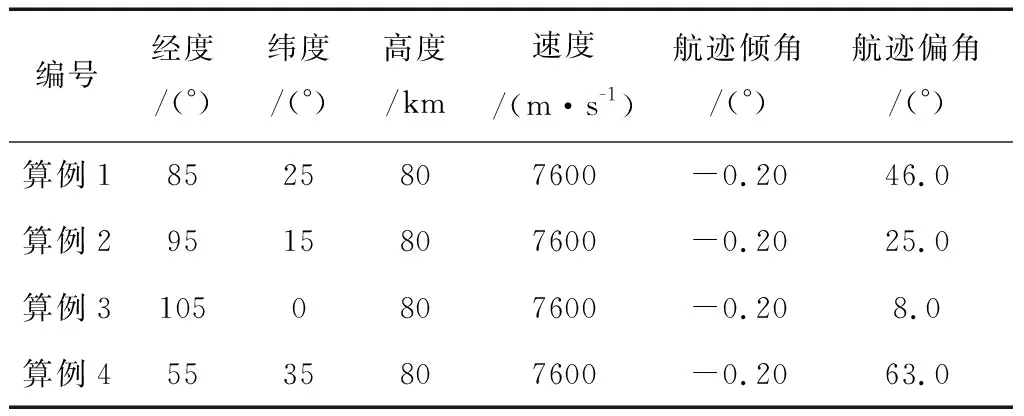
表1 初始条件

仿真结果如图2～3所示。可见在标称状态下，基于卡尔曼滤波的速度-高度剖面预测校正制导律能够满足飞行约束条件，轨迹变化平缓，精度较高。

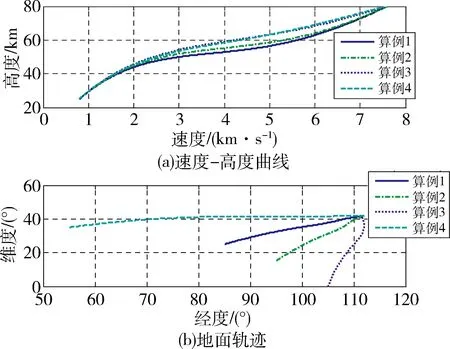
图2 不同算例下标称再入轨迹

相比于文献[12]所展示的数值预测校正制导算法(NPC)，本文制导指令生成速度更快。NPC制导复现时，制导周期选择为1s，预测步长选择为5s，积分方式采用欧拉积分，本文算法制导指令生成速度与之对比如下。

表2 全飞行段生成一个制导指令所需时长

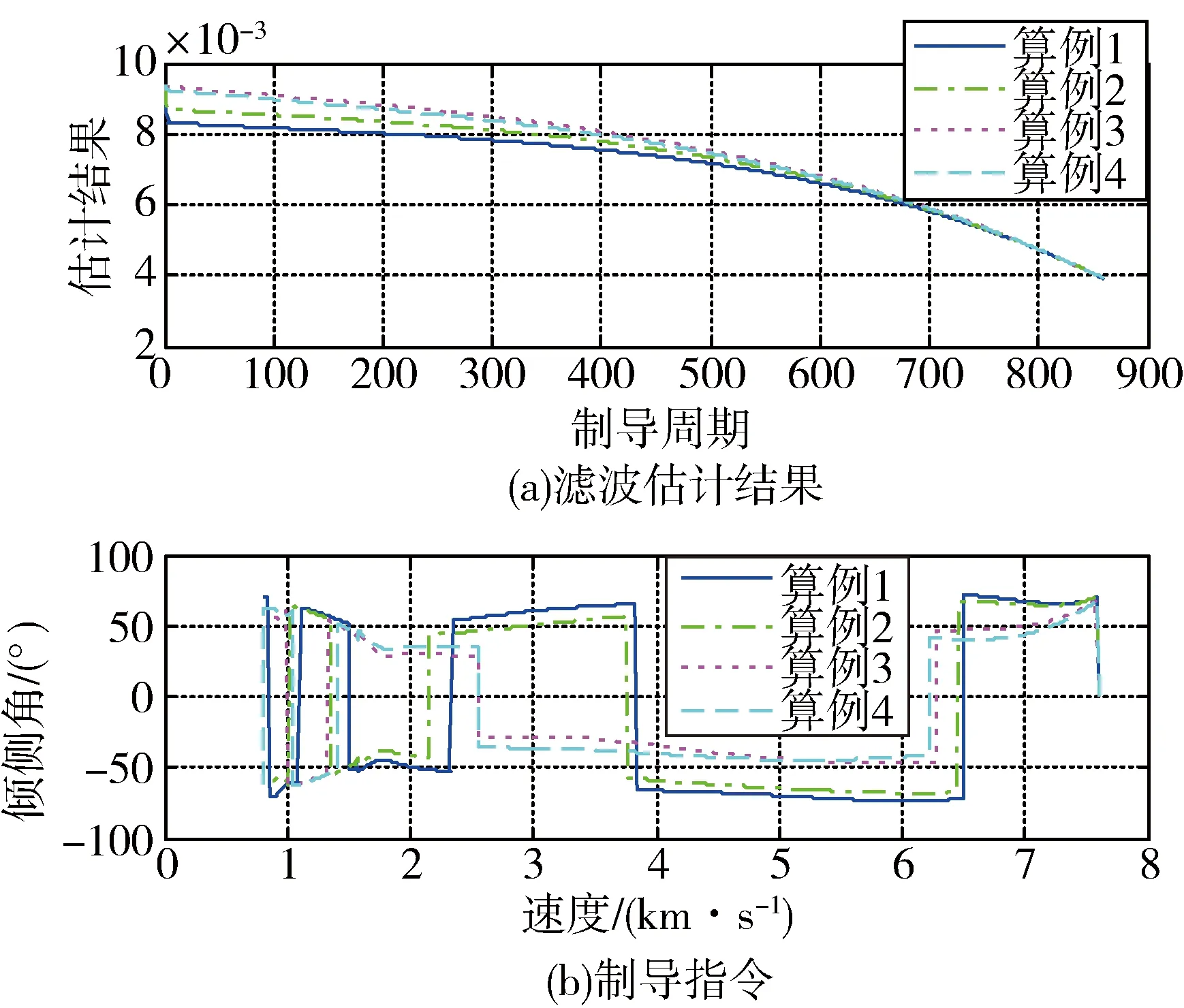
图3 无量纲高度滤波结果及制导指令

3.2 参数扰动状态仿真

考虑参数初始状态偏差及不确定性参数辨识初值偏差，针对算例4，利用蒙特卡洛仿真校验算法鲁棒性，仿真次数设定为300次。初值偏差均取为随机偏差(表3)，升力系数、阻力系数、大气密度、攻角偏差取为随机偏差和固定偏差的组合(表4)。

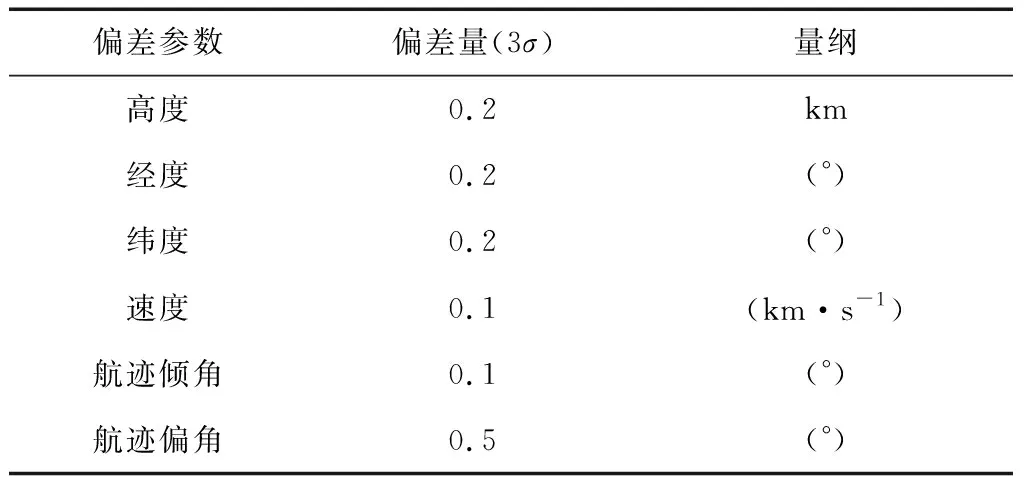
表3 初值参数偏差

表4 过程参数偏差

仿真结果如图4～6所示，图4是偏差条件下飞行轨迹，可见制导律能够适应偏差工况。图5是对应的辨识结果和制导指令，算法制导指令变化较为平滑，无发散现象。图6是再入交班点分布，可见大部分工况下交班点在理论交班点3km以内，制导精度较高。

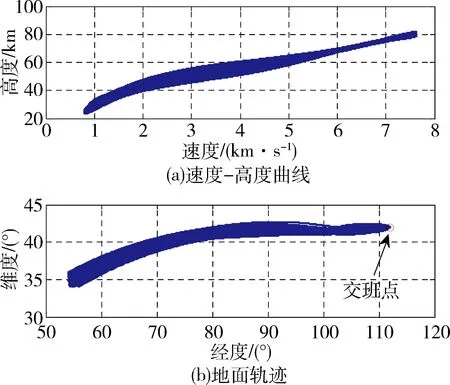
图4 蒙特卡洛仿真再入轨迹

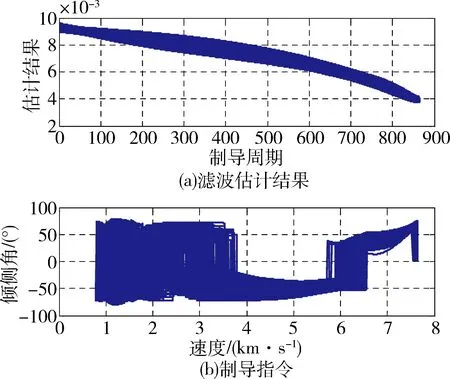
图5 蒙特卡洛仿真辨识结果及制导指令

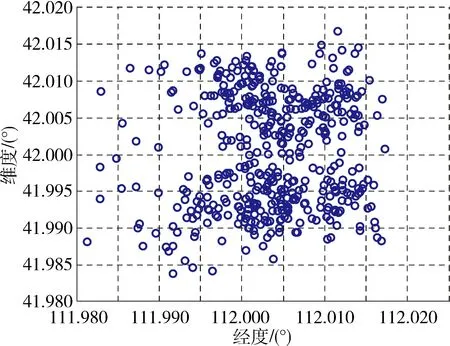
图6 蒙特卡洛仿真交班点分布

4 结论

基于卡尔曼滤波的速度-高度剖面预测校正再入制导算法，每次制导指令的生成仅需要2次单变量数值积分，相比于传统数值预测校正制导，避免了多次积分纵向运动方程，提高了实时性。针对算法末端拟合精度下降的问题，设置了更新终止条件并跟踪最后一次规划产生的标准飞行剖面，同时引入航迹倾角反馈，提升了算法在飞行末端的收敛性。

仿真表明，算法制导精度高，计算速度快，具有良好的适应性和鲁棒性。