北斗三号MEO卫星姿态预报方法研究*

邵瑞强 林 夏 龚文斌 林宝军 赵 帅

1.上海微小卫星工程中心 导航卫星研究所，上海 201210

2.中国科学院 微小卫星创新研究院，上海 201210

3.中国科学院 空天信息创新研究院，北京 100094

4.中国科学院大学 计算机科学与技术学院，北京 100094

5.上海科技大学 信息科学与技术学院，上海 201210

0 引 言

为了满足导航载荷与测控天线对地指向的需求，同时保证帆板的对日指向以获取能源，北斗三号导航系统MEO卫星常规运行过程中姿态采用动态偏航模式，在太阳高度角较小时采用连续动偏控制模式[1-3]。卫星上姿控系统将当时姿态的滚动角、俯仰角、偏航角及3个角速度传输给星内其他单机。特别的，星间链路指向控制时，需要用到当前时刻的卫星姿态信息。如图1所示，姿控系统将姿态角通过总线按秒传输给星间链路控制上位机，用于星间链路的指向计算[4]。在卫星处于自主导航时，自主运行系统也要实时计算由偏航角变化引起的相位中心变化[5-6]。除此以外，姿态的预报和计算在地面进行光压处理时也非常重要，其精度直接影响导航卫星的定位精度[7-8]。

图1 姿控信息在星内传播路径示意图

北斗三号导航系统中，星间链路起到了连接组网的作用[9]。受地面分布测站地理限制，处于境外的卫星需要由境内星中转上行控制信息和下行遥测信息。除了通信功能外，星地/星间的测距下行到地面后，采用联合定轨的方法能有效提高定轨精度[10]，显著降低设备时延对轨道和钟差解算精度的影响[11]。同时星间链路测距值也被用于北斗三号卫星的自主导航[5]。在星间链路建链时，需要上位机能够按照时隙约定计算出正确的星间链路指向角。姿控信息在星内传播时，如总线发生错误或者总线控制单机出现错误，将会影响星间链路上位机收到正确的姿态信息，从而导致建链失败，影响星间测距通信。尤其卫星处于境外时，若发生该类故障，将导致测控站无法监测卫星状态，卫星也无法获取境内更新电文，严重降低系统可靠性。在轨运行中，星间链路需要对姿态获取失败的故障情况有相应预案。

本文研究了将预报姿态应用于星间链路指向计算的方案。现有的预报姿态方法，如文献[2-3,7-8]描述的北斗三号卫星偏航姿态计算方法，在卫星处于地影时(轨道太阳角<3°)会失效，新一代北斗三号卫星(如C27)采用了与之不同的连续动偏控制。且上述文献并未对地影期连续动偏期间的细节进行分析。本文以北斗三号卫星C27为对象进行深入分析，详细描述了不同阶段姿态预报方法。利用在轨实测数据进行校验，表明预报姿态的精度满足星间链路指向计算的需求。同步计算预报姿态也可用于剔除姿态野值，提高了星间链路系统的独立性，同时提高星间建链组网的可靠性。

1 姿态预报方法

本文将姿态预报方法分为了常规时段和地影时段。地影时段中姿态出现正负变换，需特殊处理。

1.1 常规时段预报姿态计算

如图2所示，计算姿态角涉及2个坐标系:卫星质心坐标系和轨道坐标系。由于卫星质心坐标系中，天线部署在+Z轴方向，故而为了指地需求，卫星质心坐标系的+Z轴与轨道坐标系+Z轴重合，指向地球中心。卫星运动时，为了能源需求，使太阳矢量一直保持在质心坐标系X-O-Z面内。设置初始状态卫星本体系+X与轨道坐标系+X轴重合，卫星绕Z轴旋转的角度即为偏航角ψ，滚动角和俯仰角都为0。轨道太阳高度角β为太阳矢量与轨道坐标系X-O-Z平面的夹角。北斗卫星的历书精度在10m～100km范围以内[12]，利用北斗卫星历书，可快速计算出卫星任意时刻位置和其轨道太阳高度角。由于滚动角和俯仰角都为0，本文中不做分析，只考虑偏航角计算与误差。

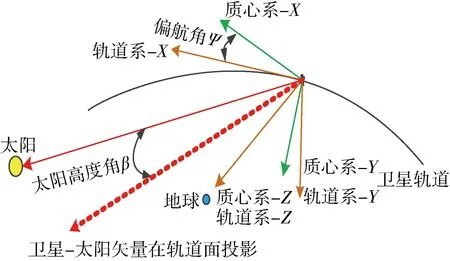
图2 卫星偏航角示意图

若卫星-太阳矢量在轨道坐标系中单位矢量为(Sox,Soy,Soz)，则轨道太阳高度角

β=arcsin(Soy)

(1)

在β较大(|β|>3°)时，计算偏航角为式(2)所示。

ψ= atan2(Soy,Sox)

(2)

其中atan2函数结果取值[-π,+π]，定义如下：

(3)

1.2 地影时段预报姿态计算

当β处于[-3°,+3°]时，卫星处于深地影区。如图3和图4所示，在1年内，北斗三号MEO卫星(C27)轨道太阳角经历2次符号变换，即2段地影期。偏航角也经历2次符号变换，按式(2)直接计算会产生偏航角符号变化。实际姿控伺服系统为减少正负变换的负荷压力，采用连续动态偏航，以使当前状态偏航角与上一状态偏航角尽量保持平稳变化。该阶段分为2部分，其一为姿态角缓慢变化到±5°，其二为±5°以内执行的阶跃变化。

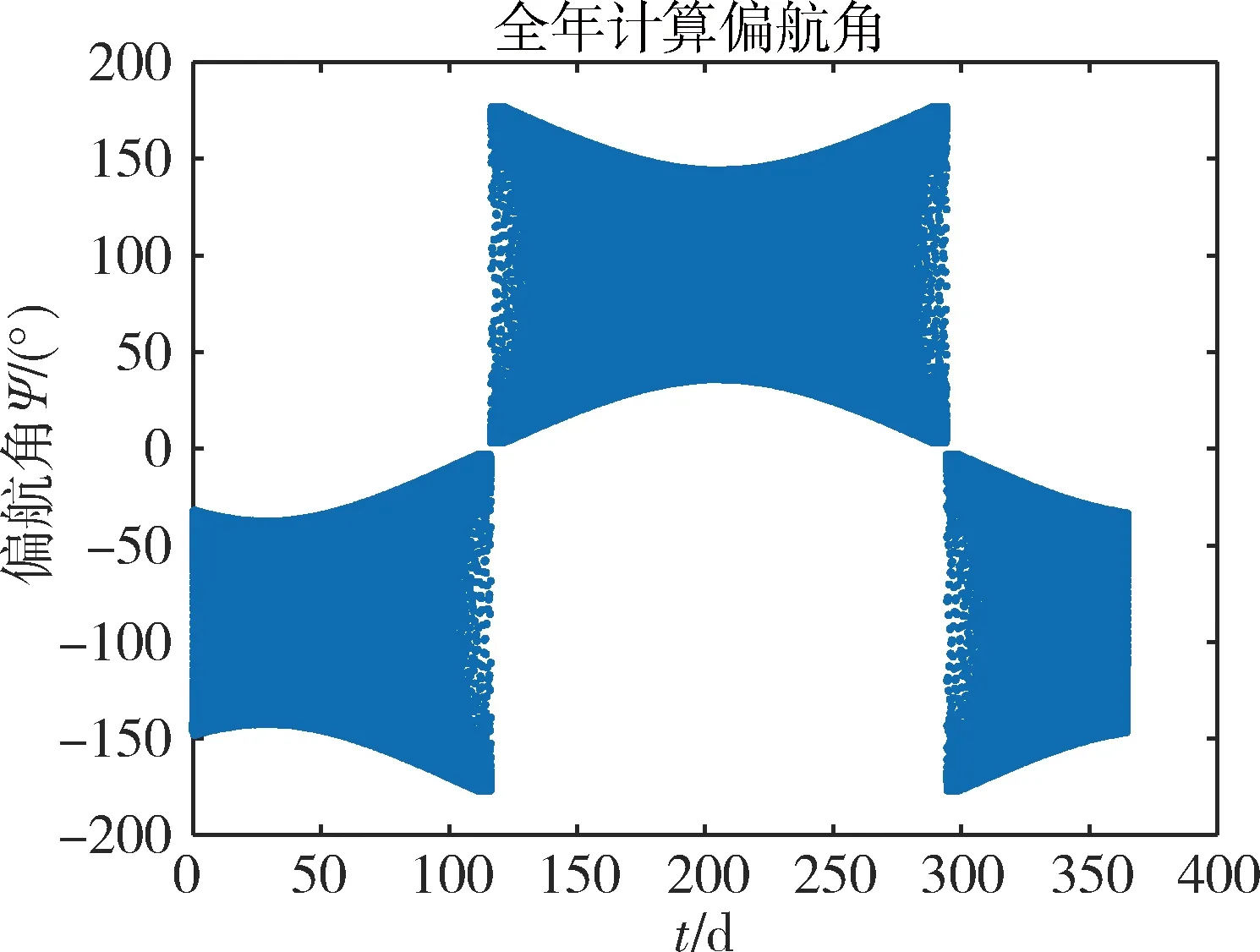
图3 根据卫星历书计算的全年偏航角

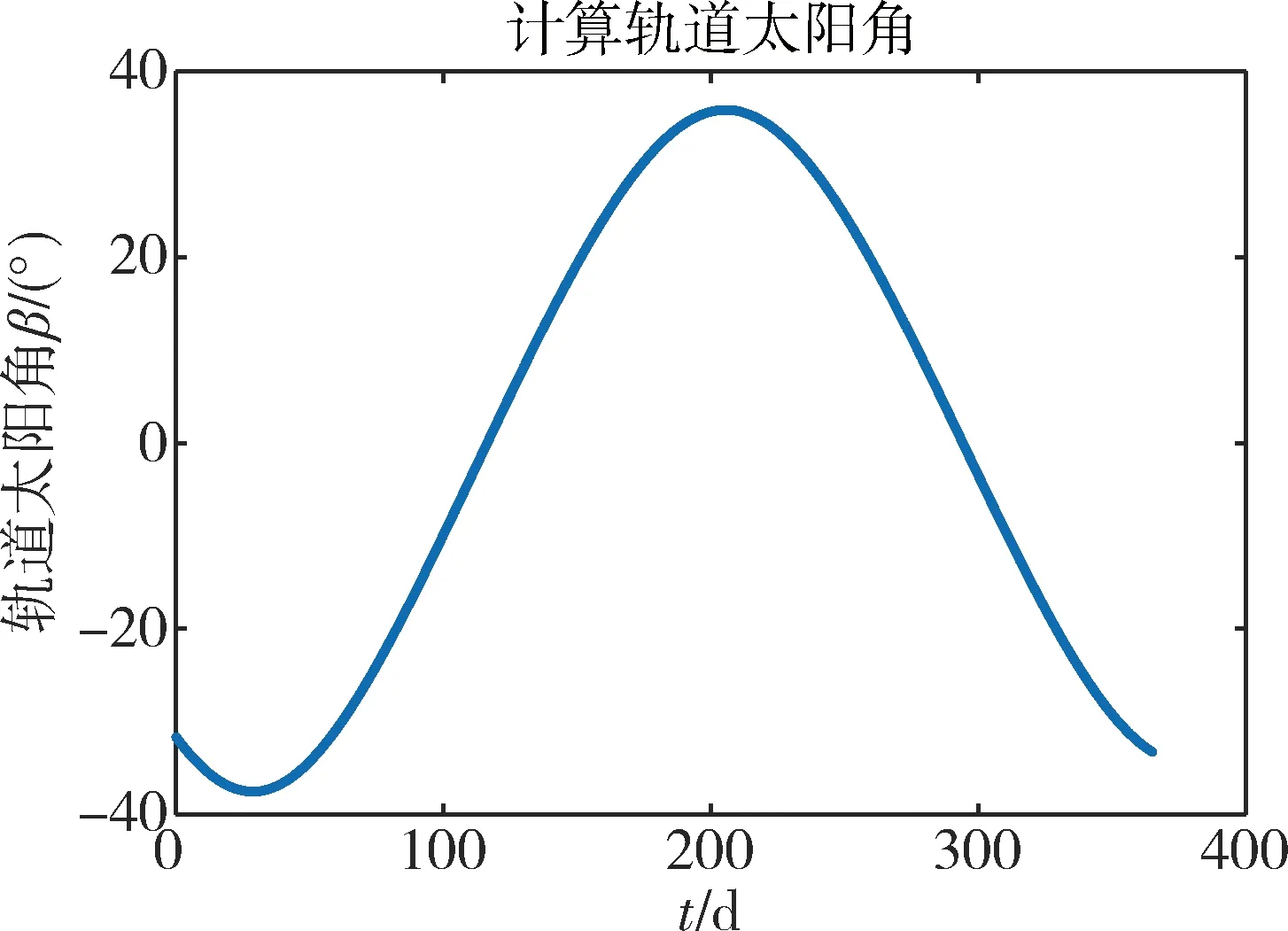
图4 根据卫星历书计算的全年轨道太阳角

1.2.1 地影时段缓变预报姿态计算

北斗导航MEO卫星的姿控系统通过比较上一状态偏航角和当前状态计算偏航角，将正负变换延时减小到±5°以内执行。假设上一状态偏航角为ψm-1，当前状态偏航角中间量用ψm表示，则按式(4)和(5)用2步计算当前状态偏航角。

(4)

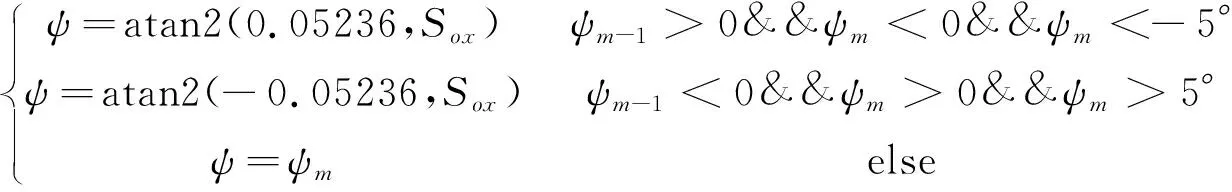
(5)

1.2.2 地影时段阶跃预报姿态计算

姿控伺服系统性能，由其本身的电学和机械学能力决定。姿控伺服系统按比例积分微分(PID)控制参数更新姿态角。由于滚动和俯仰一直保持为0，可将3个维度解耦为偏航角控制和2个维度(滚动和俯仰)的0恒定值。根据位置式PID控制算法，采样周期T取为1s，利用当前偏航信息和目标偏航信息生成控制指令Ii，写做如下公式

(6)

eψi=ψi-ψaim

(7)

eωi=ωi-ωaim

(8)

其中Kp，Ki和Kd为PID算法中比例系数、积分系数和微分系数，ψi为当前时刻偏航角，ψaim为目标偏航角，eψi为当前时刻偏航角与目标偏航角差值，ωi为当前时刻偏航角速度，ωaim为目标偏航角速度。经过一阶惯性处理，指令Ii变换为力矩输出值Mi，则角加速度αi为

αi=Mi/J

(9)

其中J为转动惯量。则更新后下一状态角加速度为

ωi+1=ωi+αi×T

(10)

下一状态偏航角

ψi+1=ψi+ωi×T+0.5×αi×T2

(11)

之后，循环迭代计算每一状态偏航角和偏航角速度，得到阶跃过程的所有状态。

2 预报姿态与实际姿态误差分析

以计算偏航角减去在轨遥测中相同时刻的在轨实际偏航角，得到预报误差。选取轨道太阳角大于3°的3个月对计算偏航角进行误差分析。如图5所示，在动态偏航期间，计算偏航角与在轨实际偏航角误差集中在0.05°以内。

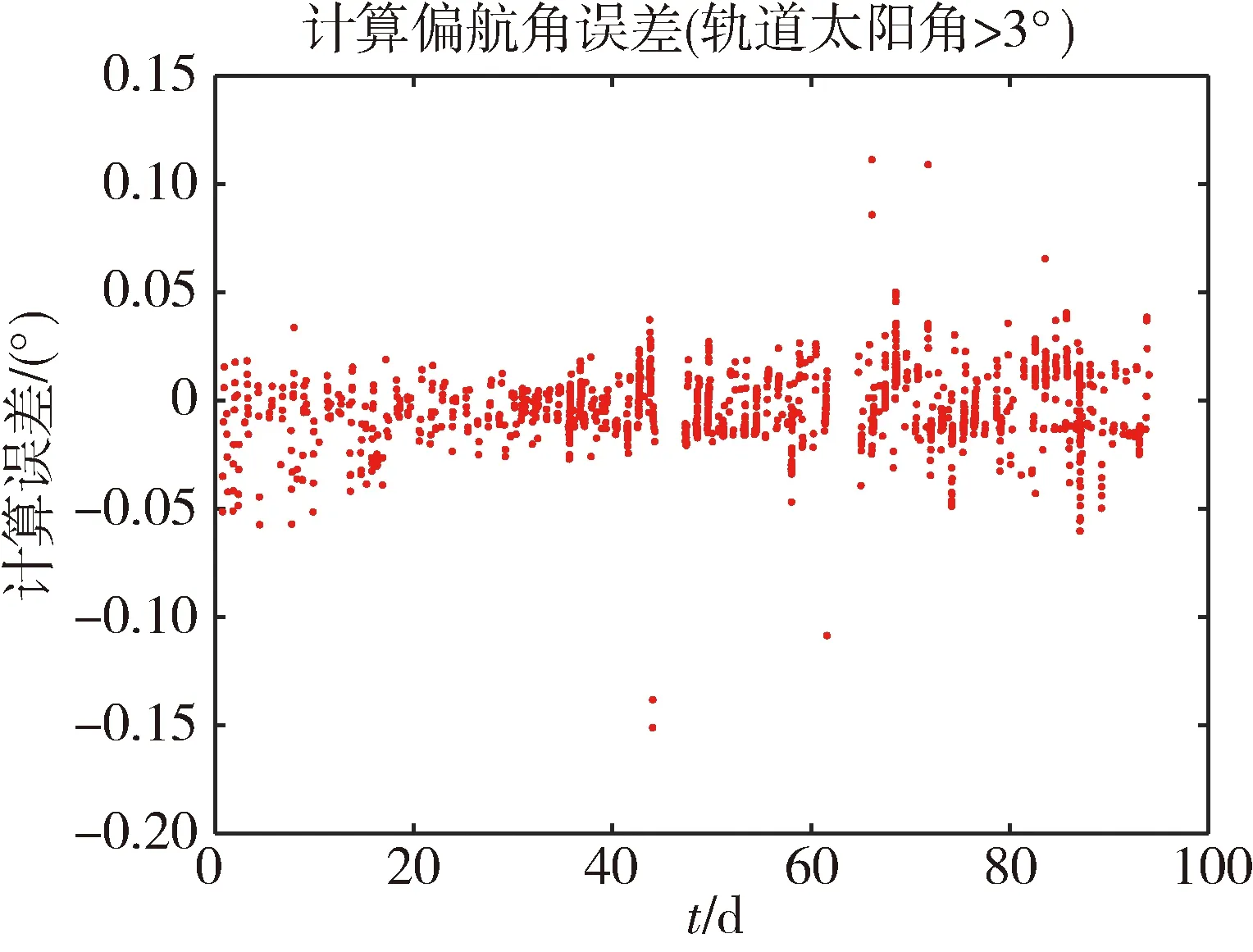
图5 计算偏航角与在轨实际偏航角误差(轨道太阳高度角>3°)

选取轨道太阳角小于3°的约12天对计算偏航角进行误差分析。如图6所示，轨道太阳角小于3°时，在绝大多数时间计算偏航角和在轨实际偏航角趋势一致，误差小于0.1°。如图7和8所示，未加入1.2.2章描述的阶跃变化过程，在姿态角正负阶跃的5min内，计算偏航角最大从+5°跳变为-5°，而在轨实际偏航角以连续曲线变换，所以最大误差达到10°，在300s的时间里，衰减为0.2°以下。

图6 轨道太阳角<3°时计算偏航角与实际偏航角趋势

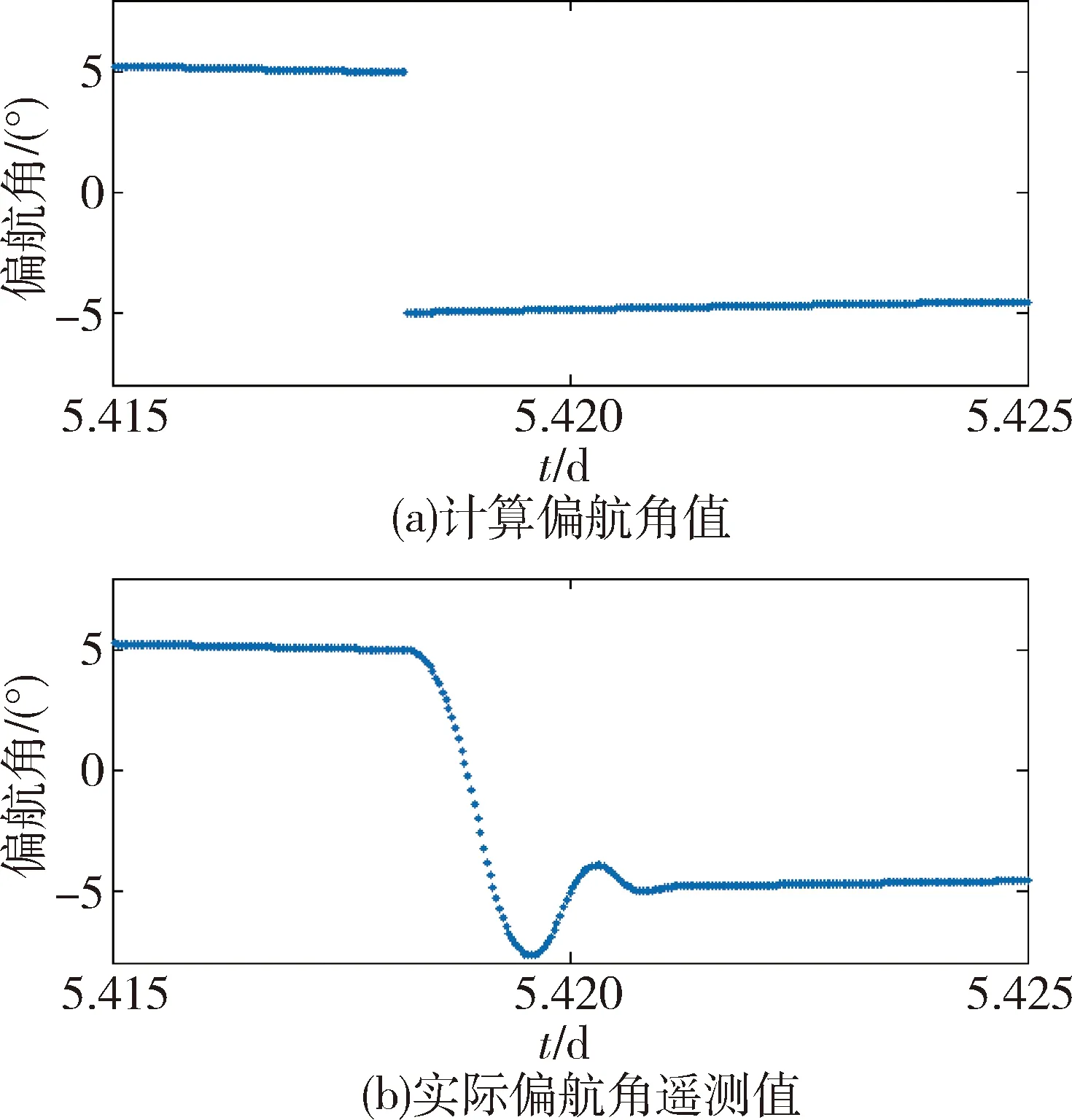
图7 偏航角正负阶跃时，不使用PID算法计算偏航角与在轨实际偏航角趋势

图8 轨道太阳高度角<3°，阶跃时段不使用PID算法，计算偏航角与在轨实际偏航角误差

如图9所示，加入1.2.2节描述的算法，计算的偏航角与在轨实际偏航角趋势完全一致，从﹢5°向-5°阶跃的过程中，持续到约200s完全重合。最大误差值约1.7°，本文提出的算法假设卫星滚动俯仰偏航3个维度完全解耦，仅计算偏航角变化。实际的姿控过程比较复杂，由于卫星转动惯量为3个维度矩阵，偏航方向的加速度变化会带来另2个方向的变化，由此另2个方向也需要计算控制才能够保持在0，因此实际曲线与计算曲线存在微小差异。

图9 偏航角正负阶跃时段，使用PID算法计算偏航角

3 使用预报姿态计算星间链路指向角误差分析

卫星偏航状态下，卫星质心坐标系+Z轴始终指地，则天线坐标系+Z轴也始终指地。如图5所示，计算偏航角误差在轨道太阳角大于3°时，误差几乎为0，使用预报姿态计算星间链路指向角误差也几乎为0。本文仅选取轨道太阳角为0°附近的1个月时间做误差分析。如图10和11所示，使用预报姿态计算卫星与另一颗卫星的指向角，离轴角误差为0，计算旋转角误差在大多数时间都在0.6°以下，最大误差1.7°，小于星间链路的波束锥角范围。

图10 使用预报姿态计算离轴角误差

在北斗MEO卫星运行时，1年经历2次地影期，则预报姿态在正负阶跃期间需使用PID算法预报，该方法能够将预报姿态100%匹配在轨实测值。在星间链路系统获取姿态角故障的情况下，该方案能够迅速恢复指向计算，从而大大提高星间链路的独立性和生存能力。

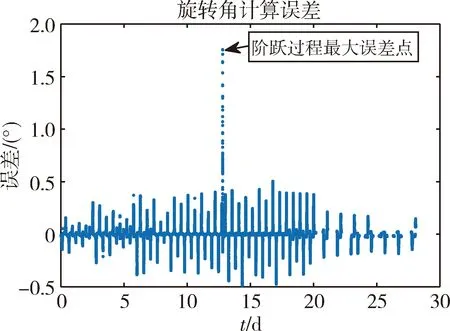
图11 使用预报姿态计算旋转角误差

4 结论

提出了将预报姿态用于星间链路指向计算的方案，并给出了计算步骤。在1年中仅2个阶跃过程中(共约10min)需使用PID算法预报，预报姿态与在轨实际姿态的误差在一年内99.9987%的时间内误差都在0.2°以下，100%时间内误差在1.7°以下。使用预报姿态计算星间链路指向角，离轴角误差为0，旋转角误差在1.7°以下。使用该方案，在星间链路系统获取姿态角失败的情况下，能够将星间链路的捕获成功概率从0提高到100%，大大提高星间链路的独立性和生存能力。为下一代北斗卫星系统可靠性提升提供依据。