一种带有观测器的高速飞行器预测滑模控制方法*

田 灿 张 远 倪少波

1.宇航智能控制技术国家级重点实验室，北京 100854

2.北京航天自动控制研究所，北京 100854

0 引言

高速飞行器具有飞行速度快、航程大、响应迅速等优点，是当前各国的重点科技发展方向。高速飞行器具有强非线性、快时变性和强耦合的动力学特性，同时对于大气参数以及自身气动参数的偏差较为敏感[1]，因此对于姿态控制提出了较高要求。

近年来智能控制、滑模控制、预测控制以及多类控制方法的组合广泛应用于高速飞行器姿态控制领域[1-4]。由于动态逆强依赖于模型的精度，因而常与其他方法相结合。滑模控制是一种非连续的控制方法，不需要被控对象模型精确已知，对外界不确定性干扰及参数摄动具有较强的鲁棒性能[5-7]。但抖振问题是滑模控制的固有缺陷，阻碍了滑模控制在实际工程中的应用与发展，文献[8]将滑模控制应用于高速飞行器，并改进了滑模的切换函数，有效抑制了滑模的抖振，使其能够很快地收敛于指定值，但控制量输出不够平滑，特别是加入参数摄动后存在明显的抖振现象。文献[9]利用自适应控制得到稳定的闭环模型，使得滑模面偏离有限，基于此设计了Winged-Cone模型的自适应滑模控制器，有效抑制了抖振，但该方法依赖于飞行器状态量可以精确获得，没有考虑到飞行器攻角存在不可避免的测量误差。近年来，预测控制对带约束、非线性、不确定性的控制问题所具有的优良性能引起了学者们的研究兴趣，并尝试将其应用于飞行器控制领域，文献[10]利用泰勒展开推导了具有解析形式的预测控制律，将分层预测控制方法用于高速飞行器，取得了预期的控制效果，但是该方法对控制器参数较为敏感，需要精细化整定控制器参数，且控制效果易受参数摄动的影响。同时传统的预测控制计算量大，多适用于慢动态过程和具有高性能计算机的环境。因此，研究一种适用于高动态特点的高速飞行器系统且弱依赖于计算性能、同时具有强抗扰能力的预测控制方法显得十分有意义。

本文针对高速飞行器巡航段的速度和高度指令跟踪控制问题，设计了一种基于线性扩张状态观测器的预测滑模控制方法。首先对飞行器纵平面非线性模型进行反馈线性化；其次通过优化性能指标推导出具有解析式的预测滑模控制律，并用Lyapunov稳定性理论证明其稳定性；然后设计线性扩张状态观测器用于补偿飞行器参数偏差和内部系统不确定性模态，提高控制器的控制性能；最后通过数值仿真对比验证了该方法的有效性。

1 系统描述

1.1 高速飞行器纵平面模型

采用NASA兰利研究中心公开的高速飞行器纵平面模型[11]：

(1)

(2)

(3)

(4)

(5)

转动惯量Iz、质量m及相关参数的具体数值参见文献[11]。在巡航条件下(Ma=15,h=33528m,δT=0.183,α=0.0315rad,δe=-0.0066rad)飞行器的线性模型开环特征：s1=-0.8，s2=0.687，s3,4=-0.0001±0.0263j，s5=0.0008。s1,2为对应俯仰角速度和攻角的短周期模态，s3,4为对应速度和航迹倾角的慢衰减长周期模态，s5为高度对应的不稳定模态。

1.2 模型反馈线性化

根据式(1)～(5)所述的模型，选取速度v、弹道倾角θ、高度h、攻角α和俯仰角速度ωz作为状态变量，节流阀开度的设置值δTc和升降舵偏角δe作为控制量。为了显含控制量δTc和δe，需要对式进行3次微分、对式(3)进行4次微分。引入发动机二阶模型如式(6)所示，对飞行器模型进行反馈线性化如式(7)所示。

(6)

(7)

其中ξ和ωn分别为发动机阻尼和自然频率，与控制量不相关的向量A的表达式如下

(8)

式中

控制增益矩阵B表达式如下

(9)

式中

2 控制器设计

控制器的设计目标为：设计合理的节流阀开度的设置值δTc和升降舵偏角δe的预测滑模控制律，使飞行器能够跟踪速度指令Vd和高度指令Hd。通过反正切跟踪微分器估计飞行器攻角和航迹倾角，通过线性扩张状态观测器估计飞行器速度和高度通道的“总扰动”。具体的控制系统框图如下：

图1 高速飞行器预测滑模控制框图

2.1 预测滑模控制

针对速度、高度反馈线性化系统式选取t时刻的滑模面

(10)

其中ev=v-vc，eh=h-hc，速度通道的滑模面系数k11，k12和高度通道的滑模面系数k21，k22和k23均满足Hurwitz条件，对滑模面求一阶导为

(11)

取辅助状态z，记为

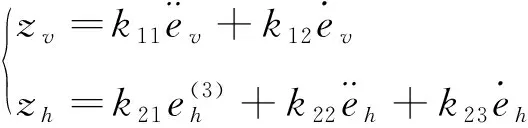
(12)

则滑模面的一阶导数可以写为

(13)

对式(13)进行Taylor展开可以得到滑模面在预测时域T>0时刻的预测值为

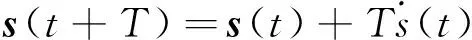
(14)

取性能指标函数为[12]

(15)

由性能指标J取极小值的条件∂J/∂u=0，即

(16)

可得预测滑模控制律为

u=-(1/T)B-1[s+T(A+z-Yc)]

(17)

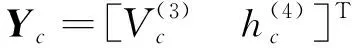
定理1：针对式(1)～(5)所述非线性系统，控制律采用式(17)，系统是Lyapunov稳定的。

证明：选取Lyapunov函数为

(18)

则Lyapunov函数对时间的一阶导数为

(19)

将式(7)、(13)和(17)代入得

(20)

因此系统在预测滑模控制律(17)的作用下是Lyapunov稳定的。

2.2 攻角和航迹倾角估计方法

由传感器获取的攻角和航迹倾角的测量值与真值之间存在误差，因此考虑构造观测器，在线估计飞行器的攻角α和航迹倾角θ用于预测滑模控制律设计。由于飞行器的纵平面模型式(3)中的速度V和高度h可通过机载装置获得相对准确的量测值，因此基于式(3)对航迹倾角θ进行在线估计：

(21)

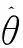
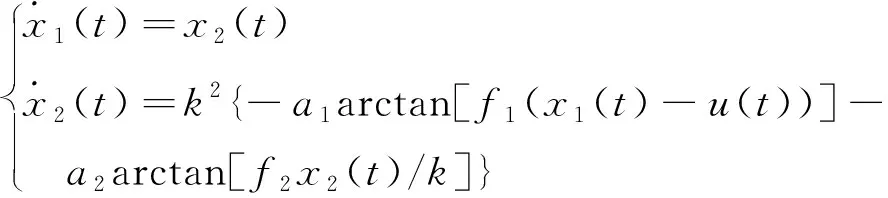
(22)

飞行器在纵平面内攻角α、俯仰角ϑ和航迹倾角θ有如下关系：

α=ϑ-θ

(23)

2.3 线性扩张状态观测器

进一步将反馈线性化后的飞行器系统式(7)改写为

(24)

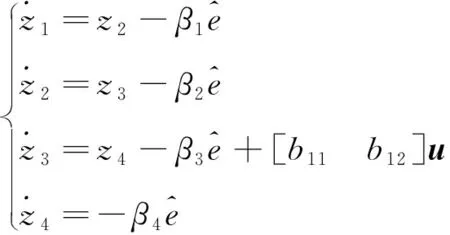
(25)

(26)

3 仿真校验

为了验证前文所述方法的有效性，进行150s的数值仿真。飞行器仿真初始状态如表1所示，并在式(27)所示的6个参数额定值中加入随机变化量来表示参数的不确定性。

表1 飞行器初始状态

(27)

飞行器执行机构的工作范围参见式

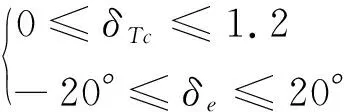
(28)

为了改善控制器的性能，给阶跃指令信号安排过渡过程，其形式为

(29)

其中yc=[vchc]T为处理后的指令用于输入给预测滑模控制器；y0=[v0h0]T为指令初始值；yd=[vdhd]T为指令的终值；a=0.03为调节过渡时间的因子。高度指令设置为h0=33610，hd=34200；速度指令设置为v0=4590，vd=4620；控制器参数设置如下：预测时域T=0.2；滑模面参数k11=20,k12=8，k21=0.43，k22=0.43，k23=0.06。速度通道LESO参数β1=20，β2=30，β3=70，β4=80；高度通道LESO参数β1=10，β2=10，β3=20，β4=60，β5=5.7。仿真结果如下。

由图2～4可以看出就速度指令跟踪而言，LESO+PSMC方案的最大误差为-1.023(m/s)而PSMC方案的最大误差为-1.226(m/s)，且前者收敛速度明显优于后者；就高度指令跟踪而言：虽然LESO+PSMC方案28.8m的最大误差略大于PSMC方案27.1m的最大误差，但是LESO+PSMC方案的稳态误差接近于0，而PSMC方案则存在约为-2.7m的稳态误差，验证了本文所设计的LESO+PSMC控制方案在飞行器参数摄动下的优越性。

图2 速度指令跟踪效果

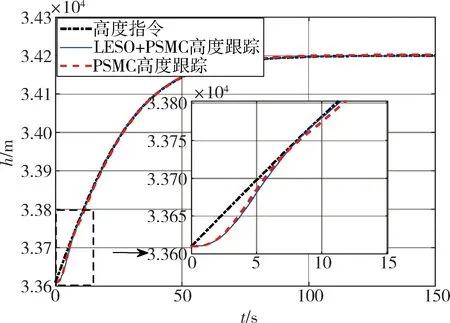
图3 高度指令跟踪效果

图4 速度和高度指令跟踪误差

图5 飞行器攻角、俯仰角速度、弹道倾角响应

由仿真结果可以看出飞行器纵向通道状态全程没有剧烈变化，攻角的最大值约为3.6°，俯仰角速度最大值约为2(°)/s。

由图6～7可以看出2种控制方案的控制量都不会超过执行机构的约束，且控制量变化幅度较为平稳，具有一定的工程应用价值。

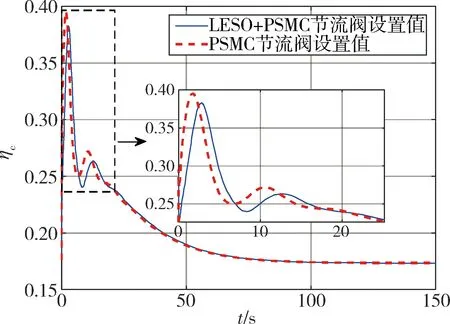
图6 节流阀设置值

图7 升降舵偏角

图8 LESO对的观测曲线

图9 LESO对的观测曲线

图8～9反映的是LESO的估计性能，其中速度和高度通道的理论值忽略了由飞行器状态量的估计误差引起的偏差，参考式(8)中向量A的计算方法并加入式(27)所示的参数偏差。由仿真结果可以看出，LESO的估计值在初始时刻与理论值存在一定误差，但误差能以较快速度收敛到0。同时可以看出LESO对速度通道的估计效果明显优于高度通道，潜在原因为高度和速度存在积分相关的关系，也存在观测器性能问题。本文采用了线性状态观测器对反馈线性化的模型进行观测，势必会忽略部分细节信息，不过从最终的控制效果来看，现有的估计误差已经能够满足控制器的要求。

4 结论

针对高速飞行器巡航段速度和高度指令跟踪控制，考虑部分状态量不可准确测量的约束，提出了一种带有观测器的预测滑模控制方法。仿真结果表明，对于不加观测器的预测滑模控制器，本文所设计的方法拥有更快的跟踪误差收敛性能、更好的控制精度，线性扩张状态观测器能够较快地对扩张状态进行有效估计，具有一定的工程应用价值。然而，考虑到估计精度及收敛时间可进一步优化，后续将考虑非线性扩张状态观测器或者有限时间收敛扩张状态等估计方法提升性能。