基于MPSP的固体运载器能量耗尽管理方法

李 烨 张 琳 薛晨琛 杨立杰 李迎博

1.中国运载火箭技术研究院，北京 100076

2.首都航天机械有限公司,北京 100076

0 引言

固体运载器发动机推力终止的通常方案是在发动机的顶部安装几个反向喷管，接到关机指令后，反向喷管产生向后的推力平衡向前推力，实现总推力为0。而固体运载器总是希望能够取消其推力终止系统，以增加其结构强度和装药量。因为安装推力终止系统需要在发动机壳体上开几个大孔，影响壳体强度的同时也增添了加工的困难。取消推力终止系统后，要研究的问题变为在发动机总能量固定的条件下，如何能在推力燃料耗尽时正好达到需求的能量状态。

近些年关于运载器能量管理问题研究逐步成为热点[1-4]，该问题的主要解决方案是通过控制姿态角与待增速度之间的角度关系来耗散多余能量，传统方式是六段式姿态角调整方法，根据飞行任务的能量要求，在制导前确定出所需要调整的最大姿态角增量，飞行时直接跟踪设定好的姿态角梯形曲线。但这种方法属于开环方式，所以抗干扰性差，精度较低，且当需要耗散的能量过多时，姿态角调整过于剧烈。目前闭环能量管理方式是主要的研究方向，其中最常用的是通用能量管理(GEM)，它简单、精确、抗干扰性强，但会导致起止点攻角较大[5]。针对该问题，徐衡等针对大气层外飞行器，提出样条式能量管理[6](SEM)，得到满足关机点的速度大小和方向，但该方法使助推末段姿态角快速变化，且不具备高度约束。张志健等利用开普勒轨道和能量守恒方法提出了满足高度、倾角约束的耗尽关机闭路制导方法[7]。

上述方法都具备很高的能量管理规划精度，但由于计算量较大，都需要提前规划好需要的耗散曲线，装订到运载器，飞行时再进行跟踪控制，不具备在线重新规划的条件，抗风险能力不足。本文提出一种基于模型预测静态规划(Model Predictive Static Programming，MPSP)的能量管理规划算法，具有较高的计算效率，具备在线应用的潜力。

1 问题描述

本文问题面向多级固体运载器的上面级，该飞行阶段已处于大气层外或大气密度很小，忽略空气阻力，可用式(1)进行描述。

(1)

式中v0为初始速度矢量，vf为期望的终端速度矢量，Tf为关机时间，P为发动机推力矢量，m为运载器质量，g为重力加速度矢量。上式可以理解为通过设计推力矢量函数P(t)，实现式(1)的两端相等，在空间中描述示意如图1所示。

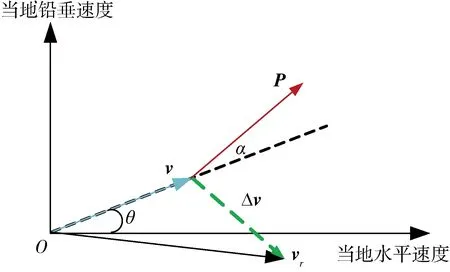
图1 运动模型示意图

将式(1)转换为动力学微分方程模型式(2)

(2)

式中，α表示攻角，θ表示弹道倾角。这里将三维空间能量管理约束到了俯仰平面上，选取控制量为攻角α，为保证运载器与载荷的分离安全，要求攻角在关机时处于0°。最终要求的终点约束条件为Yf=[vfθf]T,αf=0。

2 基于MPSP的能量耗散方法

2.1 MPSP基础算法

模型预测静态规划的方法是Padhi将模型预测控制(Model Predictive Control，MPC)与近似动态规划(Approximate Dynamic Programming，ADP)结合形成的，近些年在控制领域被广泛研究[8-12]。MPSP算法最显著的特点是通过引入一个静态拉格朗日算子，将带有终端约束的最优控制问题转换为一个静态优化问题，快速得出解析的关于终端误差的控制量修正量。

这里考虑一般的非线性系统，其表达式可写为

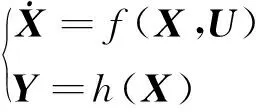
(3)

其中X∈Rn，U∈Rm，Y∈Rp。其离散化形式可以写为：

(4)

其中k=1,2,…,N-1表示离散时间步数，N为结束时间的步数。MPSP方法的目标是求解一组控制序列Uk，使最终的输出YN达到期望值YNd；并通过设定相应指标，使得到的输出序列满足控制能量最小的要求。将YN在YNd处展开：

(5)

同时，对式(4)对进行泰勒级数展开并忽略高阶项，可得误差传播方程为：

(6)

(7)

然后将dXk迭代展开直到k=1得：

dYN=AdX1+B1dU1+B2dU2+…+BN-1dUN-1

(8)

式中系数为

(9)

(10)

状态初始误差dX1=0，则式(8)简化为

(11)

式(11)中控制敏感矩阵Bk可以通过下面反向递归求解的方法计算，即在给定一组Uk后的一次预测过程结束后，由终点状态量回溯计算前面的每个离散步骤下的Bk。

(12)

(13)

(14)

对于式(11)中，通常未知变量个数(N-1)远大于等式方程的个数p，所以解并不唯一，这里需要引入其它约束来构建一个完整的最优控制问题，选取如下目标函数：

(15)

(16)

式中λ为拉格朗日乘子，将式(16)代入(11)后，得：

-Aλλ+bλ=dYN

(17)

其中

(18)

假设Aλ非奇异，通过式(17)可以求得λ的表达式为：

(19)

将式(19)代入式(16)得到控制序列修正量关于终端误差的表达式：

(20)

得到控制序列在时刻k=1,2,…,(N-1)的修正后数值：

(21)

这里要说明的是，上述控制序列更新过程中运用了小误差量近似的方法，因此这个修正过程需要迭代进行数次后才可求得使YN达到YNd的解。

可以看出，MPSP方法是一种非常有效率的算法，主要表现为：

1)与经典的最优控制理论不同，在整个控制量求解过程中只需要提供相应的共态变量即可；

2)共态变量的计算只是象征性的，在最终的表达式中已由其他变量代为表示；

3)控制敏感系数阵Bk可以递归求解；

4)迭代次数与初值选取关系较大，但当初值选取误差较小时，可以很快计算出结果，这项特点可以有效应用在在线修正计算上。

2.2 能量管理控制曲线快速计算方法

为实现控制序列的快速计算，将攻角控制量αc设为如下多项式形式：

αc=aMt3+bMt2+cMt+dM

(22)

式中aM,bM,cM和dM为待定参数，根据第2节的分析，这里代入能量管理起始点和终止点的控制约束条件αc0=αct0,αcf=0，表征控制序列在开始时平滑不发生阶跃，在关机时回到0°；将上述两个终端条件代入式(22)中，可以求得cM,dM与aM,bM的关系方程：

(23)

dM=αct0

(24)

将(23)、(24)代入(22)，整理得

αc=aMta+bMtb+t*

(25)

其中

(26)

进一步可得到控制量修正表达式：

(27)

其中上标0的变量表示上一轮迭代计算出的控制序列值，将式(27)代入(11)中，整理得到终端状态误差和控制量误差的关系表达式：

dYN=Oλ-Aλ·aM-Bλ·bM-Cλ

(28)

式中，

(29)

Bk即MPSP基础算法中的修正量系数，可由式(12)～(14)反向递归计算求得；这里建立的系统方程中Y为二维向量，控制量U为一维，所以上式中Oλ，Aλ，Bλ和Cλ均为二维列向量，可以看出式(28)构成的方程与待定参数数量相等，不用再设计最优指标匹配未知数的维数，这里直接推导得到控制量的解析表达式为：

(30)

得到参数aM,bM,cM和dM后即完成了一轮计算，实现了由dYN反馈修正攻角指令曲线的目的。将该攻角指令重新代入系统微分方程进行积分计算，判断dYN是否满足精度需求，如不满足则重复上述流程，继续修正攻角曲线参数。一次控制曲线的完整计算流程如图2所示。

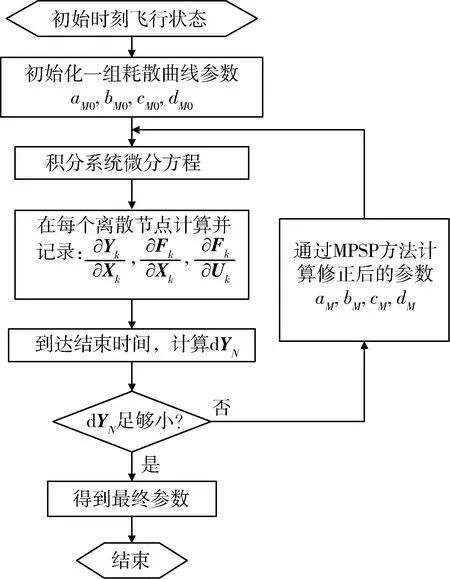
图2 能量管理参数计算流程

使用该方法在线计算时，可以通过当前运动状态作为积分求解的初值，并以实际攻角作为控制量αc的初值αc0对αc(t)进行实时求解。耗散曲线参数aM,bM,cM和dM初值可以采用上轮计算的成果，这样可以极大减少该轮迭代计算的次数。这里给出的耗时曲线在线计算方案如下：

1)发射前首次计算耗散曲线，并将曲线参数保存并装订至飞控程序内；

2)当飞行至能量耗散阶段时，利用装订的曲线参数作为迭代求解初值，采集实时运动状态作为积分初值求解耗散曲线；

3)用在线求解的耗散曲线参数代替装订值，用于下一轮的参数修正。

3 仿真分析

设定仿真初始速度为5000m/s，初始攻角αc0为-20°，初始质量为3430kg，燃料秒耗量18.7 kg/s发动机推力49500N，工作时间100s。发动机关机时需求速度为7000m/s，弹道倾角为0°。

下面的仿真结果为在线解算的第一次攻角指令计算过程，aM,bM,cM和dM的初值选取为一条连接αc0和0°的直线。第一轮只用了7次迭代计算就完成了αc参数的确定，如表1和图3所示。图3中用长虚线表示的直线为初值曲线，红色实线为最终收敛后的攻角曲线。

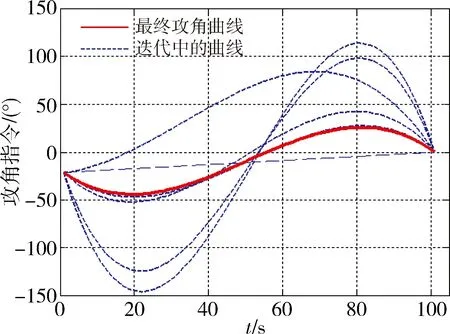
图3 攻角曲线解算过程

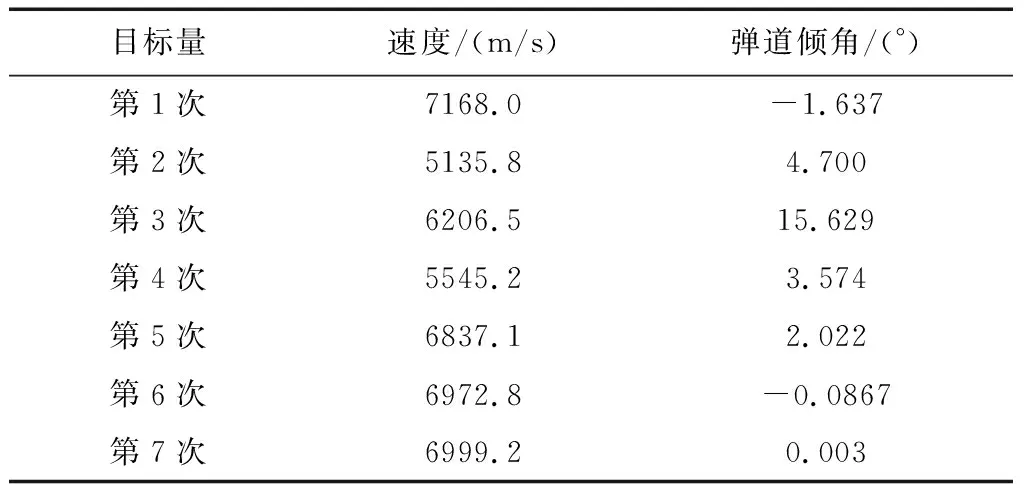
表1 迭代过程变化

在仿真过程中， 每10s进行一次在线攻角曲线重解算，以修正建模过程中未考虑的误差带来的预测偏差。仿真结果表明，利用上轮修正的曲线参数作为MPSP计算过程的初始化值，可以有效使迭代次数降为1～2次。

本文进一步分析了本方法与其他能量管理方式的异同，与最常用的GEM、SEM进行了对比分析，针对相同的仿真条件，在仿真开始进行的攻角指令解算曲线对比如图4所示。

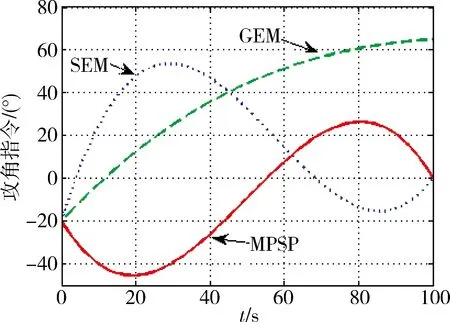
图4 不同方法的攻角曲线

通过对比发现，这3种方式都具有很高的速度控制精度，可以满足能量管理的要求。但是GEM采用圆弧轨迹拟合耗散曲线，其不具备末端控制量的约束能力，由图4可以看出末端攻角高达63°。SEM采用高阶曲线拟合耗散曲线，其终端可满足控制量的约束条件，但每次解算需要求解含有积分表达式的多元方程组，花费计算时间较长。

表2统计了3种方法的首次计算时间和飞行中在线计算的平均耗时。由结果可以看出MPSP方法在未给定初值情况下计算效率与GEM、SEM相差不多，但是在线采用基于较高精度初值的MPSP计算方法大幅度提升了计算效率，使计算周期下降到0.1s量级，具备了在线应用的能力。

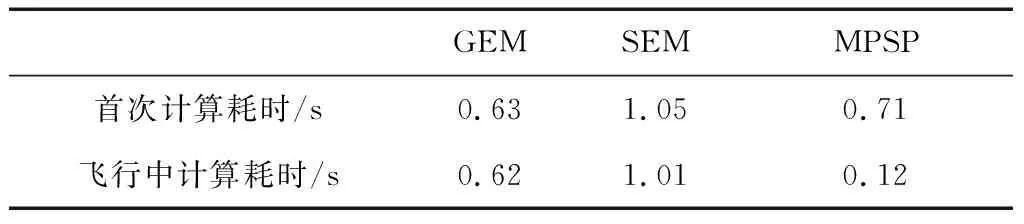
表2 解算时间统计

4 结论

针对固体运载器耗尽关机能量管理问题，本文在MPSP框架下建立了一种高效的能量耗散曲线快速确定方法，可有效准确估计攻角控制指令的参数。算法利用了MPSP算法初值误差小时可迅速收敛的特性，形成了射前离线计算标称初值，在线依据实时状态敏捷修正的在线能量耗尽管理方法。仿真结果表明，本文提出的能量管理方法不仅具备较高的精度，而且计算效率较高，可实现在线能量管理。