基于弯剪型结构简化计算模型和物理随机地震动模型的地震易损性分析

苏嘉頔 彭勇波 宁超列，*

（1.同济大学土木工程学院，上海 200092；2.同济大学上海防灾救灾研究所，上海 200092）

0 引 言

近几十年来，随着我国城镇化过程的快速发展，为满足大量涌入城市居住的人们生产、生活需要，建筑行业得到极大程度的发展，大量建筑结构涌现，城市扩张迅速[1]。与此同时，我国地处环太平洋地震带和欧亚地震带交汇处，是世界上地震灾害最为频发的地区之一。因此，在这些人口高密度聚集的城市区域，一旦发生破坏性的地震灾害，将造成重大的经济损失和人员伤亡。鉴于此，围绕现代城市区域建筑群开展地震易损性分析，对于减轻地震灾害风险，提高城市抗震防灾韧性具有十分重要的意义。

然而，由于我国各地城市普遍缺乏历史震害调查资料，因此数值解析方法是开展区域建筑群地震易损性分析的主要手段之一。在数值解析方法中，建筑结构简化计算模型和地震动选波/生成方法是研究的关键。在建筑结构简化计算模型中，剪切层模型是目前结构弹塑性时程动力响应分析的主流模型[2]。然而，剪切层模型不能反映群体建筑中多层和高层结构的弯剪耦合动力响应特征[3]。在能够反映弯剪耦合动力响应特征的结构简化计算模型中[4-7]，又存在模型参数众多、参数标定困难甚至无法标定的难题，造成这些模型应用极其不便。而在地震动选波/生成方法中[8-9]，已有的研究大多采用确定性的方式，较难全面和准确地反映地震动随机性的影响。

因此，本文围绕区域建筑地震易损性分析，提出了一类模型参数较少、计算速度快，且能够反映弯剪耦合动力响应特征的结构简化计算模型。同时，为了全面和准确反映地震动随机性的影响，通过引入物理随机地震动模型，结合概率密度演化理论，建立了一类适用于区域建筑地震易损性分析的新方法。

1 结构简化计算模型

根据已有的剪切型层模型[2-4]和连续型弯剪层模型[5-6]，同时考虑控制模型参数的数量，本文将建筑结构简化为一组弹塑性剪切层弹簧和一根弹性弯曲梁，建立了一类改进的弯剪型结构简化计算模型，如图1所示。其中，剪切层弹簧用于表征结构的剪切变形，能够进入弹塑性变形。弯曲弹性梁用于表征结构的弯曲变形，仅能够处于弹性变形。同时，模型假设结构每一层的质量均集中于楼面。与经典的剪切性层模型一致，剪切层弹簧的各质点通过非线性剪切弹簧连接，剪切层弹簧只传递剪力和横向位移。弯曲弹性梁通过弹性杆连接，弹性杆可以传递剪力、弯矩、位移和转角。剪切层弹簧和弯曲弹性梁之间通过刚性链杆连接。刚性链杆可以约束各层的横向位移保持一致。

图1 弯剪型结构简化计算模型Fig.1 Bending-shear coupled structural simplified computation model

因此，根据动力平衡条件，剪切层弹簧的运动控制微分方程可表示为

式中：Ms为剪切层弹簧的质量矩阵；Cs为剪切层弹簧的阻尼矩阵；Fs为恢复力向量；Ps为剪切层弹簧承担的地震荷载；U为结构各层的水平位移时程；̇为水平速度时程；̈为水平加速度时程。

类似地，根据动力平衡条件，弯曲弹性梁的运动控制微分方程可表示为

式中：Mb为弯曲弹性梁的质量矩阵；Cb为弯曲弹性梁的阻尼矩阵；Kb为弹性刚度矩阵；Pb为弯曲弹性梁承担的地震荷载。

将式（1）和式（2）相加，可得：

因此：

其中，M代表结构的整体质量矩阵：

式中：mi和Ji（i=1，2，…，N）分别为结构第i层的质量和惯性矩；N为结构层数；C为阻尼矩阵，可采用瑞利阻尼；Kb为弯曲弹性梁的整体刚度矩阵，可通过建立和叠加结构各层的单元弯曲刚度矩阵获得。

结构各层的单元弯曲刚度矩阵为

式中：H为层高；EI为结构每层的抗弯刚度。

另一方面，P为结构的外荷载向量：

Fs为由剪切层弹簧提供的水平恢复力向量：

式中，fsi为剪切层弹簧的恢复力，由相应的滞回模型确定。

考虑复杂的滞回模型将使得简化计算模型的参数众多且难以标定。因此，采用Steelman和Hajjar提出的滞回模型描述[10]，如图2所示。相比其他的滞回模型，该滞回模型仅包括三个参数：剪切刚度GA、剪切屈服转角ϵ和退化参数τ。因此，该滞回模型具有参数较少、标定简单且计算方便的优势。其中，退化参数τ反映了建筑结构耗能能力的退化，代表实际滞回环面积与理想滞回环面积的比。

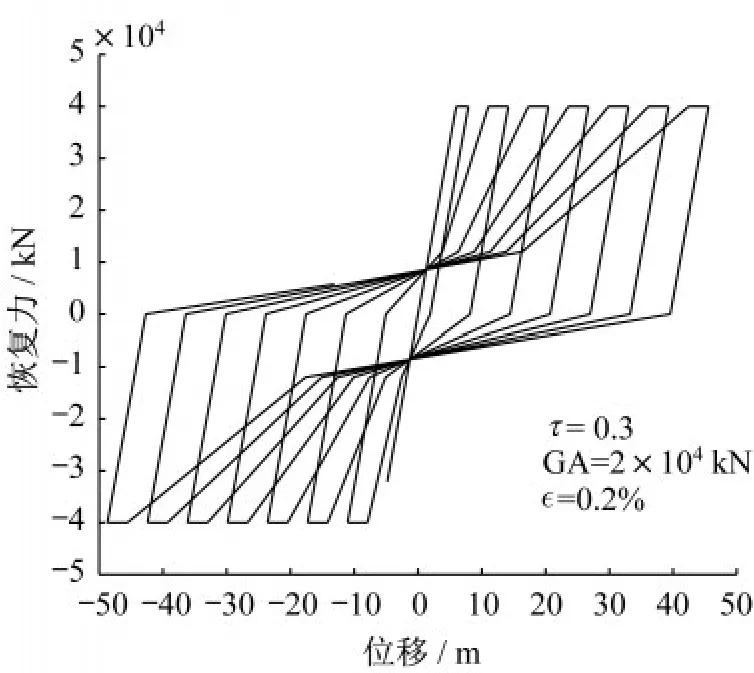
图2 滞回模型Fig.2 Hysteresis model

2 模型参数校准

综上所述，本文建立的弯剪型结构简化计算模型共有7个参数，如表1所示，分别为：等效层质量m、层高H、弯曲刚度EI、剪切刚度GA、转动惯量J、滞回模型参数τ和剪切屈服转角ϵ。显然，这7个模型参数的取值与建筑材料、结构类型、建筑年代和抗震设防水平等因素相关。不同的模型参数取值，表征不同的建筑结构，使得地震动力响应特征具有显著差异。

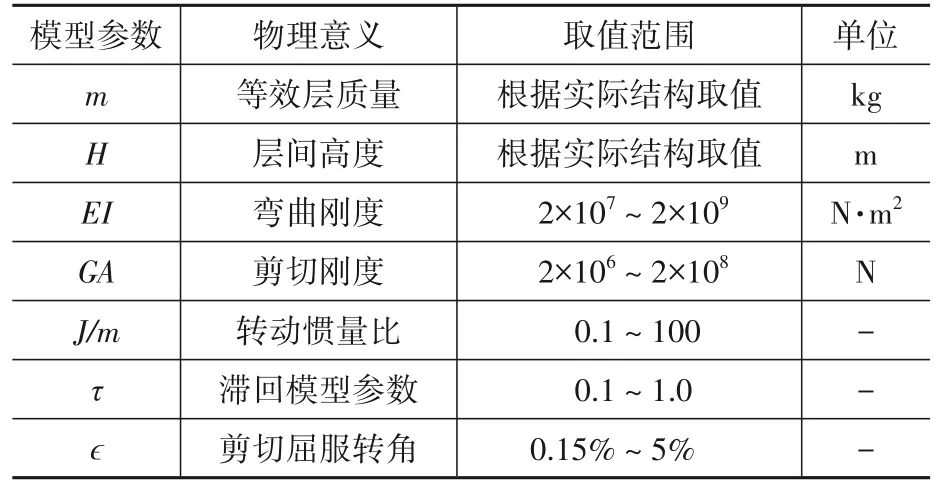
表1 弯剪型结构简化计算模型参数Table 1 Bending-shear coupled structural simplified computation model parameters

2.1 参数敏感性分析

为使本文建立的弯剪型结构简化计算模型具有良好的适用性，开展参数敏感性分析，进一步减少需要标定的模型参数数量。根据模型试算，首先设定7个模型参数的范围，如表1所示。然后，采用修正的Morris筛选法对每个参数的敏感性进行判断。修正的Morris筛选法对每个自变量以固定的步长依次变化[11]，计算相应的灵敏度判别因子S，表达式为

式中：Yi为模型第i次运行的计算结果；Yi+1为模型第i+1次运行的计算结果；Y0为模型取基准参数时的计算结果；Pi为第i次模型运算时的参数取值；Pi+1为第i+1次模型运算时的参数取值；P0为模型的基准参数取值；n为模型的运行次数。

以结构的最大顶层位移和最大层间位移角为判别指标，获得7个模型参数的灵敏度判别因子S，如图3所示。可见，在给定的模型参数区间范围内，剪切刚度GA最为敏感，其次为等效层质量m和层间高度H。弯曲刚度EI、剪切屈服转角ϵ、转动惯量J和滞回模型参数τ属于低灵敏度参数。

图3 模型参数敏感性分析Fig.3 Sensitivity analysis of model parameters

2.2 参数校准步骤

因此，固定结构的弯曲刚度EI=1.5×109N·m2，剪切屈服转角ϵ=0.2%，转动惯量与质量比J/m=1，滞回模型参数τ=0.3，建立其他参数的校准步骤，具体如下：

（1）等效层质量m：根据楼面恒载和活载取值估算。

（2）层间高度H：由结构基本属性参数获得或估算。

（3）剪切刚度GA：首先，根据建筑结构类型和建筑高度H估算获得结构的一阶自振周期。然后，假设弯曲刚度EI与剪切刚度GA的比值[12]，通过不断调整剪切刚度GA，使得结构简化计算模型的一阶自振周期与估算结果相等。

2.3 模型校准验证

为了验证模型和上述参数校准过程的准确性，本文开展了弯剪型结构简化计算模型与精细有限元模型分析结果的对比。以一栋六层钢筋混凝土框架结构为例，如图4所示，各层的楼面恒载为3.5 kN/m2，活载为2.0 kN/m2，混凝土楼板的厚度为 120 mm，柱构件为 C400×400，配筋率为1.2%，梁构件为B200×400，顶部和底部的配筋率为0.6%。钢筋采用HRB400，混凝土采用C35，采用OpenSEES程序建立精细有限元模型，具体过程见文献[13]。

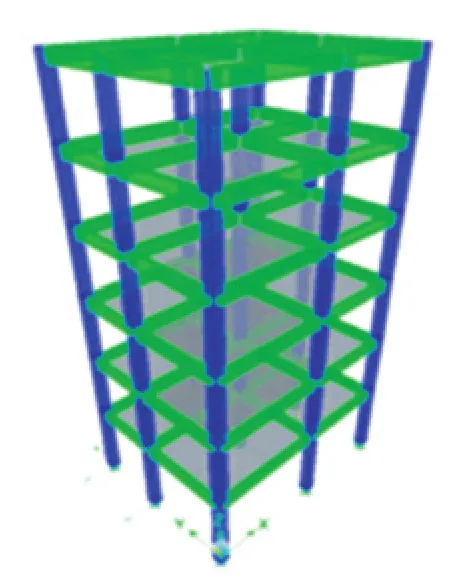
图4 钢筋混凝土框架结构Fig.4 Reinforced concrete frame structure

在基础上，从美国太平洋地震工程中心的地震动数据库中任意选择三条地震动记录作为输入（EQ1、EQ2和EQ3）。图5给出了不同地震动作用下本文建立的弯剪型结构简化计算模型与精细有限元模型最大层间位移角沿层高分布的对比。可见，本文建立的弯剪型结构简化计算模型计算结果与精细有限元模型的计算结果基本相同。层间位移角沿层高的分布呈现先大后小的趋势，表明本文建立的弯剪型结构简化计算模型能够准确反映结构的弯剪耦合变形。同时，在计算过程中，本文建立的弯剪型结构简化计算模型平均用时仅需1.5 s，而精细有限元模型的计算用时为1 min。因此，本文建立的弯剪型结构简化计算模型可以大幅度缩短计算时间，这对区域建筑的地震动力响应计算具有十分重要的意义。

图5 最大层间位移角对比Fig.5 Comparison of maximum inter-story drift

3 地震易损性分析

增量动力分析方法（Incremental Dynamic Analysis，IDA）是一类基于弹塑性动力时程响应分析的地震易损性分析方法，其基本思想是输入地震动强度逐级增大的同一地震动，对结构进行多次弹塑性动力时程响应分析，获得结构在不同地震动强度作用下的最大地震动力响应，从而较为全面地评估建筑结构的抗震性能。IDA曲线反映了结构从初始弹性阶段到弹塑性阶段，直至失稳倒塌的结构破坏全过程。然而，传统的IDA方法一般针对设定场地，通过选取或人工模拟方式，获得若干条地震动开展结构的地震动力时程响应分析。这种方式不能全面、精细地反映地震动的随机性特征。为了合理考虑地震作用的随机性，李杰等近年来提出了基于物理的随机地震动模型和概率密度演化理论，开展了建筑结构的地震响应随机分析与可靠度评价，揭示了地震动随机性在复杂非线性结构系统中的传播[14-15]。因此，本文采用物理随机地震动模型，结合概率密度演化理论，开展上述弯剪型结构简化计算模型的地震易损性分析，并与常规研究方法进行对比。

3.1 分析流程

图6给出了基于物理随机地震动模型和概率密度演化理论开展地震易损性分析的流程[19-20]。可见，分为四个步骤：

图6 基于物理随机地震动模型和概率密度演化理论开展地震易损性分析的流程Fig.6 Flowchart of seismic fragility analysis based on physical random earthquake ground motion model and probability density evolution method

（1）根据工程场地条件，采用物理随机地震动模型模拟生成一系列地震动样本，并确定其赋得概率。

（2）开展每条地震动样本在给定地震动强度作用下的结构动力时程响应分析，得到表征结构地震损伤的最大层间位移角。

（3）采用概率密度演化理论，获得最大层间位移角的概率密度分布。同时，结合设定的最大层间位移角阈值，获得结构在给定地震动强度作用下的超越概率。

（4）调整地震动样本的地面峰值加速度（简称PGA），得到结构在不同地震动强度作用下的超越概率，最终生成地震易损性曲线。

3.2 随机地震动模型

为客观反映地震动幅值和频谱的随机性，本文采用的物理随机地震动模型包括三个基本随机变量：基岩白噪声强度S0、场地卓越频率ω0和场地等效阻尼比ξ0。模型具体细节，见文献[15]。不失一般性，假设建筑结构所在的工程场地抗震设防烈度为8度，基本地震加速度峰值均值为0.3g，场地土为Ⅲ类，场地特征周期为0.45 s。因此，根据物理随机地震动模型的参数校准结果，场地卓越频率ω0的均值和标准差可取12rad/s和5.04rad/s；等效阻尼比ξ0的均值和标准差可取0.1和0.035。场地卓越频率ω0和等效阻尼比ξ0均假定为服从对数正态分布的随机变量。基岩白噪声强度S0假定为高斯过程，其傅立叶谱幅值为0.20m/s2，对应的地面峰值加速度均值为0.11g。

针对上述三个基本随机变量，采用切球选点方法模拟生成221条随机地震动样本[15]。其中任意2条地震动样本的时程曲线，如图7所示。可见，模拟生成的随机地震动样本具有较好的零均值特性和时域非平稳性。

图7 典型随机地震动时程Fig.7 Time history of typical random ground motions

图8给出了221条随机地震动样本的PGA的统计分布。可见，这221条随机地震动样本的PGA的均值为1.04 m/s2，标准差为0.34 m/s2，其直方图近似服从对数正态分布假设。

图8 随机地震动PGA的统计分布Fig.8 Statistical distribution of peak ground acceleration of random ground motion

3.3 地震易损性曲线

由上可知，随机地震动的PGA为一个随机变量。因此，采用PGA均值表征地震动强度大小，表示为E[PGA]。根据图6所示流程，对每条地震动样本按PGA的均值同等调幅，由0.01g按照0.01g的间隔依次调幅至1.0g，获得不同E[PGA]作用下结构的最大层间位移角，即：对于每一个E[PGA]都有221个最大层间位移角。然后，采用等价极值事件准则，基于概率密度演化理论，引入虚拟随机过程[14]，获得给定E[PGA]作用下结构最大层间位移角的概率密度分布。

图9给出了不同E[PGA]作用下结构最大层间位移角的概率密度分布。可见，基于随机地震动模型和概率密度演化理论可获得不同E[PGA]作用下结构最大层间位移角精确的概率密度分布。与传统的对数正态分布假设对比，该精确分布在尾部区域具有一定的波动性。这种波动性在地震动强度E[PGA]较小时尤为明显。随着E[PGA]的增大，分布的波动性逐渐减小。

图9 最大层间位移角的概率密度曲线Fig.9 Probability density curve of maximum inter-storey drift ratio

在此基础上，将建筑结构的损伤状态划分为四个等级，分别为轻微破坏状态、中等破坏状态、严重破坏状态和毁坏状态[16]。其中，轻微破坏状态的最大层间位移角阈值取1/550；中等破坏状态、严重破坏状态和毁坏状态的最大层间位移角阈值分别取轻微破坏状态阈值的2倍、4倍和10倍。图10给出了不同E[PGA]作用下结构的地震易损性曲线。可见，当E[PGA]为0.1g时，该结构有50%左右的概率发生轻微或中等以上的破坏，基本不会发生严重破坏；当E[PGA]为0.2g时，轻微破坏难以避免，同时有70%的可能性发生中等破坏，40%左右的概率发生严重破坏；当E[PGA]达到0.3g时，结构有50%以上的概率发生严重破坏；当E[PGA]达到0.6g时，严重破坏难以避免。

图10 地震易损性曲线Fig.10 Seismic fragility curve

3.4 结果对比分析

为验证本文建立方法计算结果的准确性，进一步开展与已有研究方法计算结果的对比。因本文采用的结构为一栋6层钢筋混凝土框架，因此搜集已有文献中6层钢筋混凝土框架结构的地震易损性曲线，如图11所示。其中，卢飞[17]采用PKPM软件对一栋6层三跨钢筋混凝土框架结构进行精细有限元建模，并基于对数正态分布假定，计算获得了以PGA为地震动强度指标的地震易损性曲线。杨硕[18]采用MSC.MARC软件对一栋6层钢筋混凝土框架结构进行了地震易损性研究，获得了以PGA为地震动强度指标的地震易损性曲线。采用F偏差对比不同破坏状态下三条曲线的差异性，可得：轻微破坏、中等破坏、严重破坏和毁坏状态下本文获得的地震易损性曲线与卢飞、杨硕等人获得的地震易损性曲线相差较小，F偏差分别为1.455 3与1.520 8、1.415 2与1.329 4、1.203 4与1.131 5、0.909 5与2.542 0。

图11 地震易损性曲线对比Fig.11 Comparison of seismic fragility curves

4 结 论

围绕区域建筑地震易损性分析需求，提出了一个模型参数较少、计算速度快、能够反映弯剪耦合效应的结构简化计算模型。同时，考虑地震动随机性的影响，基于物理随机地震动模型和概率密度演化理论，建立了一种适用于群体建筑地震易损性分析的新方法。主要研究结论如下：

（1）建立的弯剪型结构简化计算模型仅需标定三个模型参数：剪切刚度GA、等效层质量m和层间高度H，即能较好反映建筑结构在地震作用下的弯剪耦合动力响应特征，计算结果与精细有限元模型计算结果吻合良好。相比精细有限元模型，本文模型的计算效率提高了近40倍，这对大规模群体建筑地震易损性分析具有十分重要的意义。

（2）基于物理随机地震动模型和概率密度演化理论开展建筑结构地震易损性分析，能够更加精细和全面地反映地震动随机性对建筑结构地震损伤特征的影响。其中，不同地震动强度作用下结构最大层间位移角的概率密度分布与传统的对数正态分布假设存在一定的偏差。随着地震动强度增大，这种偏差逐渐减小。

需要指出的是，本文采用的是IDA方法开展建筑结构的地震易损性分析。这一方法需要增量调幅随机地震动样本强度，因此计算量仍较大。为了降低计算量，同时保证每个样本点均属于随机动力计算，可进一步采用云图法，结合物理随机地震动模型生成建筑结构的地震易损性曲线。