局部支承功能梯度板的自由振动分析

韩振南，随岁寒，2，刘金建

（1.商丘工学院 机械工程学院，河南 商丘 476000；2.无锡金元启信息技术科技有限公司，江苏 无锡 214000）

为了完成各种极端环境下的任务，近年来，许多工程领域都对结构的材料性能提出要求，复合材料因此被广泛应用于各种场合[1-3]。虽然铁和铜等金属在常温下具有良好的强度与韧性，但处于高温条件下时，其强度与韧性都大幅降低，并且金属材料极易被腐蚀。而陶瓷具有良好的耐高温与耐腐蚀性能，但是它的韧性较差。金属与陶瓷常被选用为复合材料的原材料，以期得到耐高温耐腐蚀的高韧性高强度材料。但是传统的复合材料采用层合结构，将材料简单地粘合在一起，金属与陶瓷之间存在明显的分界面，材料性能的突变导致层间出现应力集中，特别是在高温下，结构容易出现分层、裂纹和其他损伤[4-5]。

为了克服传统复合材料的上述缺陷，沿着板厚逐渐改变材料成分的功能梯度材料被提出[6]。相比传统复合材料，它的优势在于材料性能的平滑变化缓和了材料的应力集中现象，显著提高了耐高温性与耐磨性，同时降低了热应力残余[7-8]。依赖于其优越的材料性能，功能梯度材料在被提出后的几十年内被广泛应用于土木工程、航空航天、交通运输与生物医学等领域，各种功能梯度结构的力学行为分析也成为研究热点。文献[9]采用谐波微分求积法研究了具有内线支承的轴向运动功能梯度板的振动特性。文献[10]基于一阶剪切变形理论，研究了液体环境中不同类型的孔隙率分布、流体深度和长宽比等参数对功能梯度多孔板自由振动的影响。文献[11]采用扩展正弦板理论，研究了磁场、电载荷和梯度指数等参数对简支功能梯度压电板弯曲的影响。文献[12]基于Mindlin板理论，研究了纵横比、厚长比、幂律指数值和不同边界条件对功能梯度矩形板自由振动的影响。近年来也有很多学者关注含孔隙功能梯度材料板[3，13]以及纳米功能梯度板[14-15]的动力学问题。以上研究表明功能梯度材料对环境适应性强的优点，因而众多学者采用各种方法研究其材料参数和外界环境因素对功能梯度结构的动力学和静力学特性的影响，极大地扩展了功能梯度材料的应用场景。

以上文献大都关注了功能梯度结构的动力学特性，而边界条件对结构动力学特性有重要影响[16-17]，对于方形板结构，这些文献主要关注固支、简支和自由等边界条件，且这些边界条件一般贯穿整条边。然而，工程应用中很难做到四边完全固支或简支，常常会出现一个边界上只有局部有支承的情形，因此研究局部支承条件下的功能梯度板具有实际意义，目前这方面的研究还比较少。由于局部支承的特殊性，解析法、复模态法和Galerkin 法等方法难以处理，而有限元法能处理局部支承条件，建模方法简单且便于与ANSYS 软件的计算结果进行对比，以验证本文方法的准确性。本文基于Mindlin板理论，假设板的材料是由陶瓷和金属组成的功能梯度材料，利用虚功原理建立局部支承功能梯度板的有限元方程，重点研究了100%、50%和25%3种支承条件下系统的自由振动特性，并分析了振动特性与梯度指数间的关系。

1 控制方程

如图1所示，考虑一个长a、宽b、厚h的功能梯度矩形板，红色代表局部支承长度。功能梯度板由陶瓷和金属混合物制成，上表面为陶瓷，下表面为金属，其材料特性被认为符合幂律函数。则功能梯度板的弹性模量E和密度ρ可分别表示为

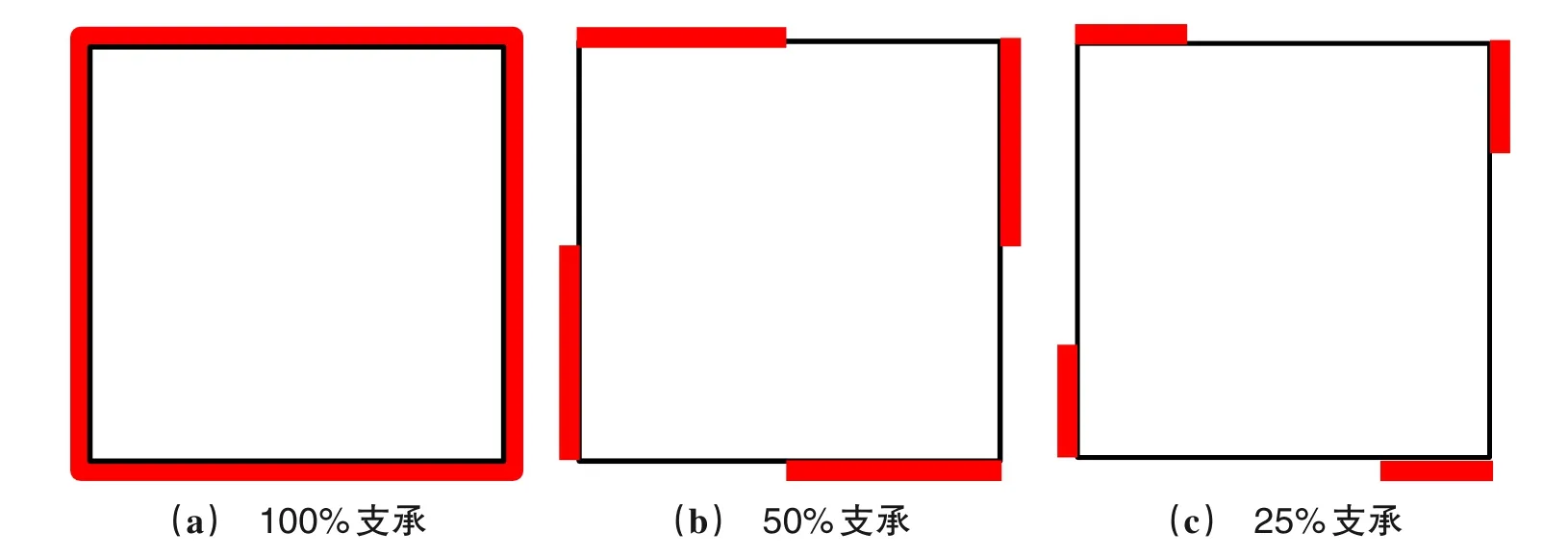
图1 3种支承条件下的功能梯度板Figure 1 Functional gradient plate under three supporting conditions

功能梯度板的物理方程可以表示为

2 数值算例

式（12）结合边界条件可以解得各阶固有频率及其模态，本文采用四边固支（简称CCCC）和四边简支（简称SSSS）两类局部支承边界条件来对功能梯度板的振动问题进行数值分析，功能梯度板的材料性能参数与几何参数如表1所示。

表1 物理参数值Table 1 Values for physical parameters.

为验证本文建立的有限元模型的正确性，分别利用本文方法和ANSYS软件计算了纯金属和纯陶瓷板的前三阶固有频率，并在图2～4给出了四边固支陶瓷板对应的100%、50%和25%支承的模态，四边简支的板的模态图形有类似形状，篇幅所限不再给出。对比可见，随着支承范围的缩小，各阶模态变化明显：第一阶模态表现出逆时针旋转的特性，但最大振幅处仍然在板的中心位置；第二阶模态仍然有两个最大振幅，但最大振幅位置逐渐向局部自由的边界处靠近；第三阶模态更加复杂，从面内四个最大振幅过渡到边界上四个最大振幅。由式（1）可知，梯度指数的变化意味着材料密度和弹性模量的变化，k=0代表纯陶瓷板，k=+∞代表金属板。前三阶固有频率分别在表2～4给出。由表2可见，100%固支支承时随着模态阶次升高误差增大，第三阶固有频率误差为1.27%；100%简支支承时有类似规律，不同的是第三阶频率的误差仅为0.86%，说明本文方法更适用于简支条件。ANSYS采用10 000个SHELL181单元，每个节点6个自由度。本文方法采用400个单元，每个节点3个自由度。正是由于单元数量和节点自由度的差异导致本文结果的误差。表3和表4分别为50%和25%支承时的对比数据，误差与100%支承接近，但是采用了2 304个单元，说明在局部支承时需要更多的单元来满足精度要求。

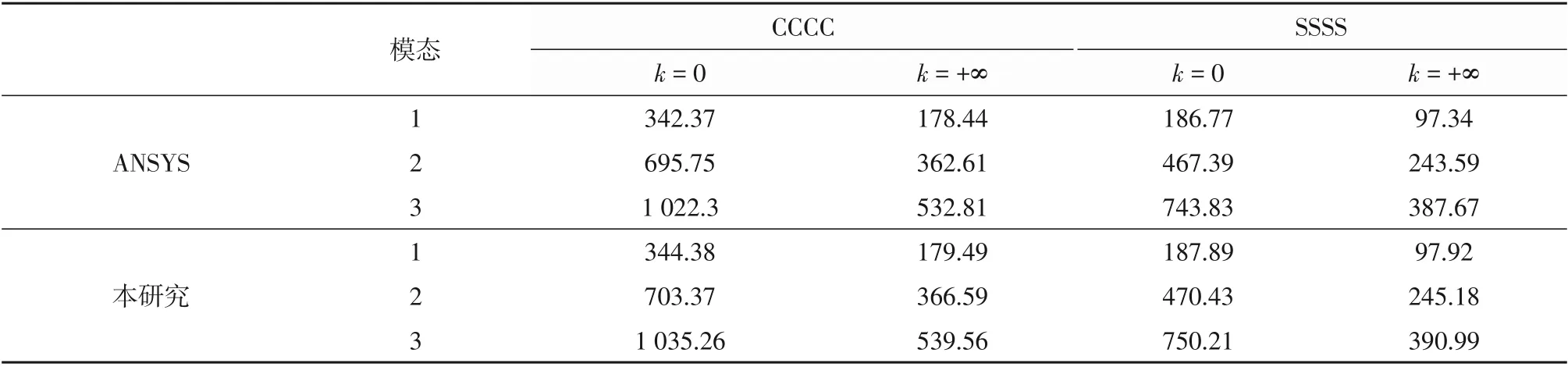
表2 100%支承前三阶固有频率对比Table 2 Comparison of the first three order natural frequencies with 100%support

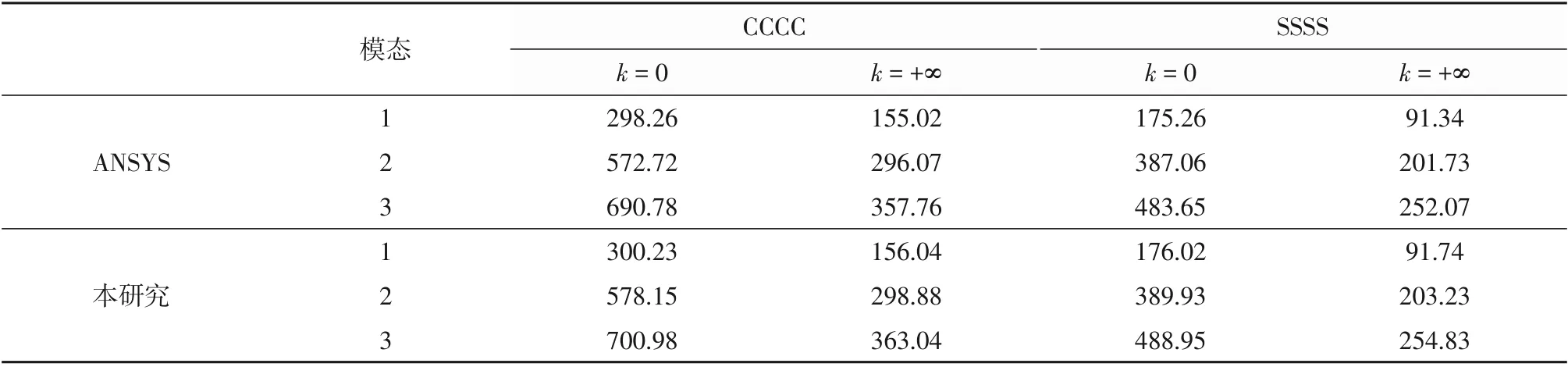
表3 50%支承前三阶固有频率对比Table 3 Comparison of the first three order natural frequencies with 50%support

表4 25%支承前三阶固有频率对比Table 4 Comparison of the first three order natural frequencies with 25%support

图2 固支100%支承下陶瓷板前三阶振动模态Figure 2 The first three vibration modes of ceramic plate with 100%fixed support

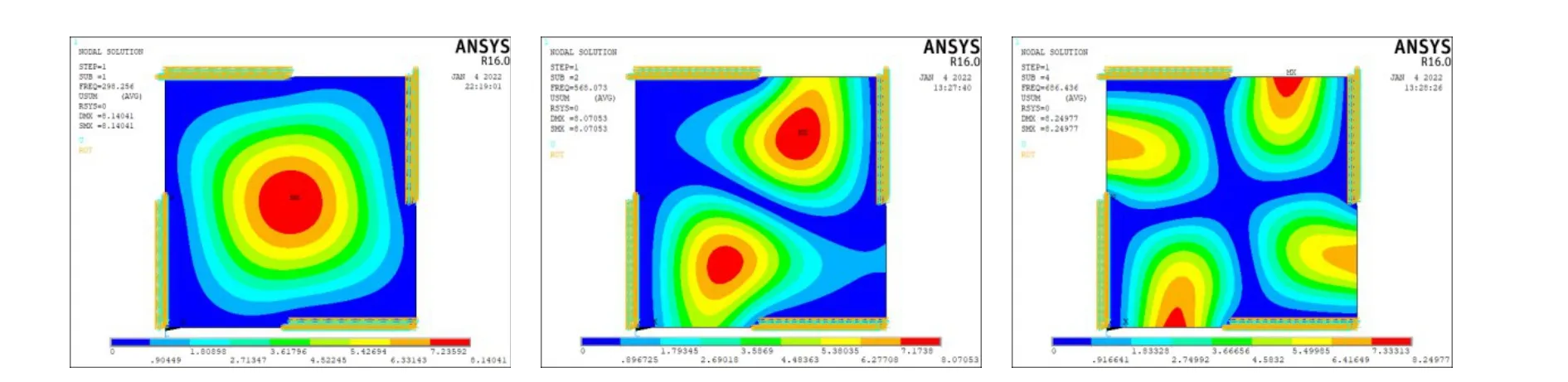
图3 固支50%支承下陶瓷板前三阶振动模态Figure 3 The first three vibration modes of ceramic plate with 50%fixed support

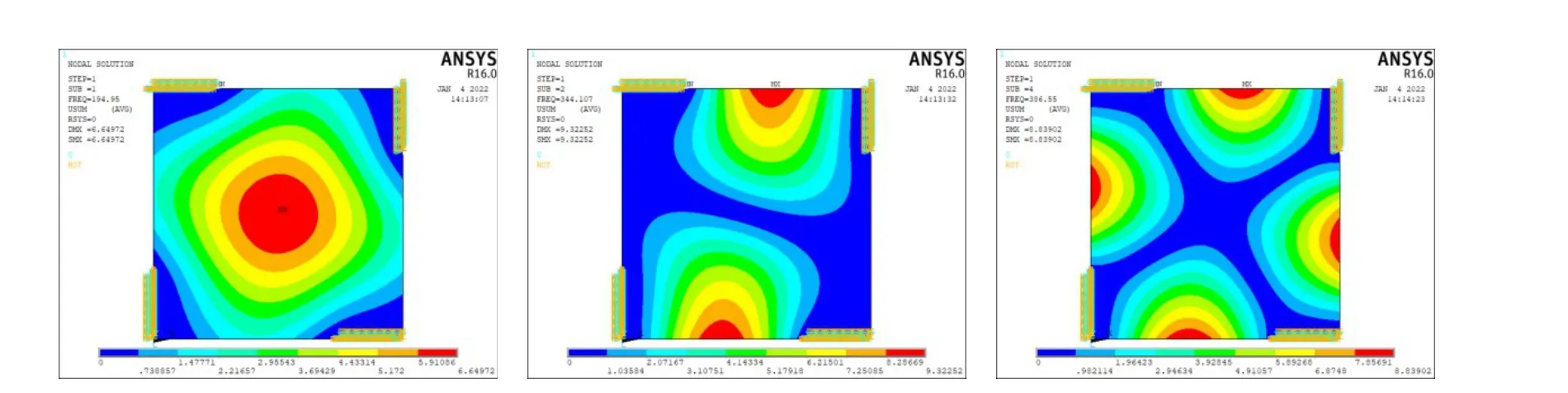
图4 固支25%支承下陶瓷板前三阶振动模态Figure 4 The first three vibration modes of ceramic plate with 25%fixed support

图5～7给出了100%固支和简支条件下的前三阶固有频率随梯度指数的变化规律，梯度指数对固有频率的影响及其成因已有较多报道[14-15]，这里不再赘述。对比3 种支承范围可以发现，支承由100%降低到25%时，固支边界对应的一至三阶固有频率分别降低约43%、50%和62%，而简支边界对应的一至三阶固有频率分别降低约37%、47%和61%，这一规律与梯度指数无关。同时，图5中100%固支支承时，第二阶和第三阶固有频率的数值分别接近第一阶固有频率的2倍和3倍；而图6中50%固支支承时，这一关系为1.91倍和2.3倍；在图7中25%固支支承时这一关系为1.76倍和1.96倍，同样这一规律也与梯度指数无关。由于第二和第三阶固有频率相对第一阶固有频率的倍数在减小，且这两个倍数在数值上也逐渐接近，这使得图6和图7的第二阶和第三阶频率看起来更接近。

类似地，图5中100%简支支承时，第二阶和第三阶固有频率的数值分别接近第一阶固有频率的2.5倍和4倍；而图6中50%简支支承时，这一关系为2.2倍和2.7倍；在图7中25%简支支承时这一关系为1.9倍和2.3倍，这一倍数关系比固支板更大，同样这一规律也与梯度指数无关。因此局部简支的第二和第三阶频率看起来差值更小。据以上现象可以进一步推论，随着支承范围的进一步减小，第一阶固有频率将进一步降低，同时第二和第三阶固有频率在极限情况下将重合。

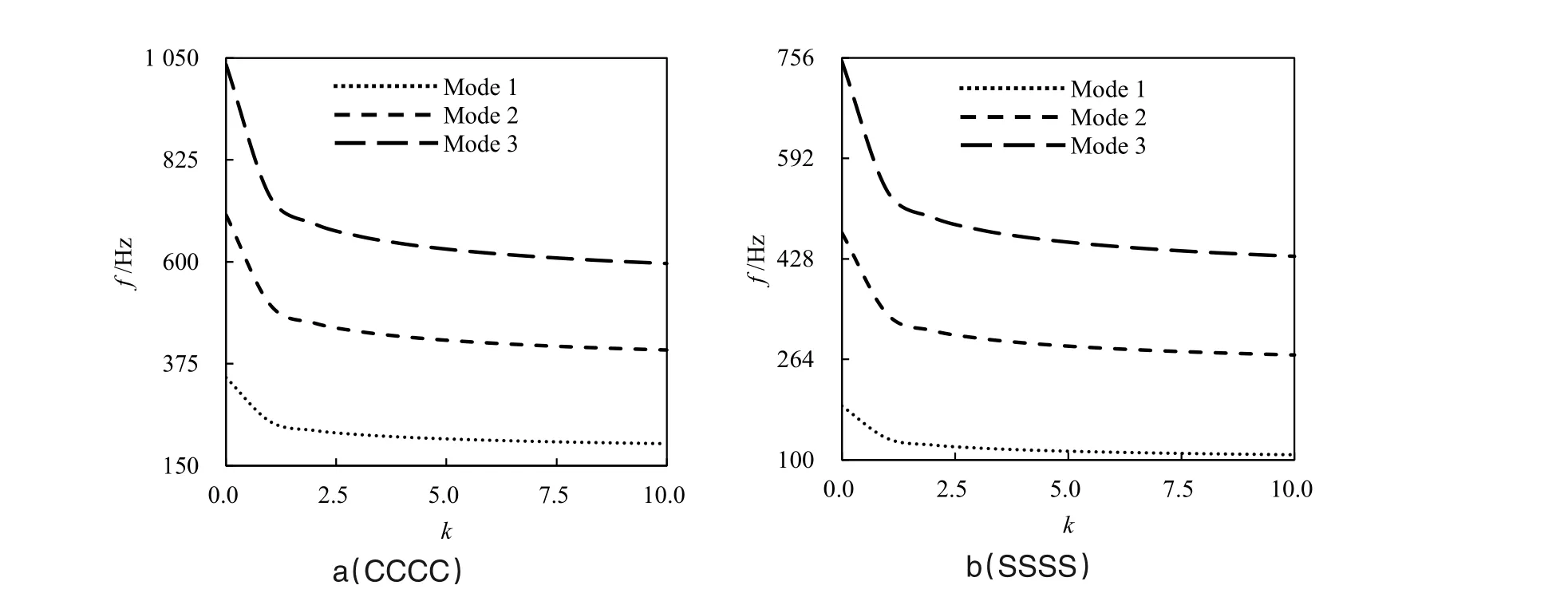
图5 100%支承前三阶固有频率与梯度指数关系Figure 5 First three order natural frequencies vs.gradient index with 100%support

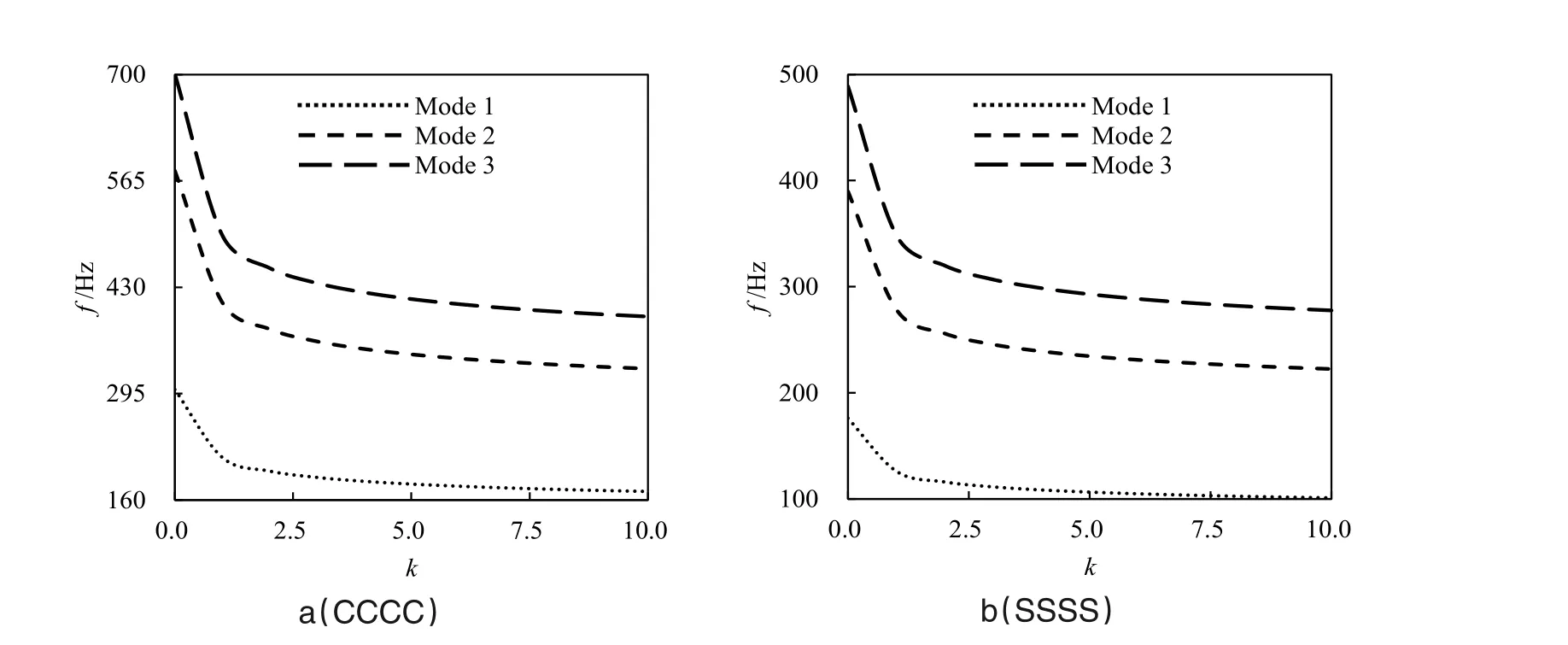
图6 50%支承前三阶固有频率与梯度指数关系Figure 6 First three order natural frequencies vs.gradient index with 50%support

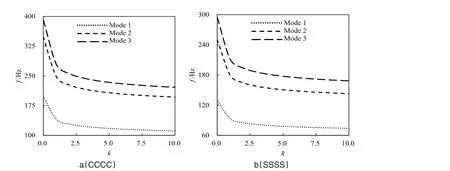
图7 25%支承前三阶固有频率与梯度指数关系Figure 7 First three order natural frequencies vs.gradient index with 25%support

3 结论

基于Mindlin板理论，采用四边形单元离散板域，应用虚功原理建立了功能梯度板的自由振动有限元模型，针对四边固支和四边简支两类边界条件，考虑各边25%、50%和100%3种局部支承条件，通过与ANSYS软件计算结果的对比，证实了本文方法的正确性，并给出了固支条件下的模态。随后分析了梯度指数和局部支承范围对系统固有振动的影响。梯度指数改变导致板材料参数变化，进而影响各阶固有频率，梯度指数越大各阶固有频率越大。随着支承范围的减小，各阶模态变化较大，同时各阶固有频率相应变化。具体体现为各阶固有频率随支承范围降低逐渐降低，但阶次越高降低的幅度越大，使得第二和第三阶频率逐渐接近，同时固支板的降幅大于简支板。