推陈出新 培养学生的创新思维

■ 武汉市第三中学 彭爱国

创新思维是指以新颖独创的方法解决问题的思维过程，通过这种思维能突破常规思维的界限，以超常规甚至反常规的方法、视角去思考问题，提出与众不同的解决方案，从而产生新颖的、独到的、有社会意义的思维成果。随着社会的快速发展，创新人才越来越受到社会的青睐，创新人才的培养也是国家进步和发展的需要。物理是一门以实验为基础的自然科学，它是发展最成熟、高度定量化的精密科学，物理学的发展有力地促进了人类文明的进步，高中物理的学习对提高学生的创新思维能力起着积极的推动作用。

在高中力学问题中，整体法、隔离法、正交分解法、合成法、图解法等这些基本方法可解决大量的力学问题，但是这些常规方法在解决有些问题时会有较大的难度，因而需要我们推陈出新，突破常规思维的界限，培养学生的创新思维，利用所学的基本知识创造性地去解决这些问题。

在涉及到转动轻杆对固连物体的弹力作用时，很多情景下因杆对物体弹力的大小和方向在不断变化，用常规方法很难解决。但如果我们能创新应用基本的物理方法，就可很巧妙的解决问题。下题是笔者在教学过程中发动学生一题多解，推陈出新，由学生提出的三种解法，在此与各位同行分享。

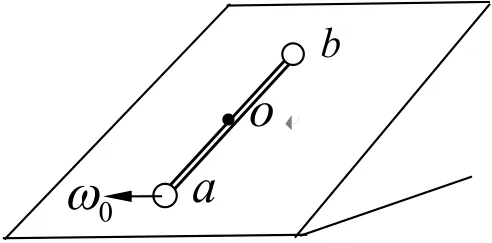
A.在轻杆转过1800的过程中，角速度先减小后增大

B.只有ω0大于某临界值，系统才能做完整的圆周运动

C.轻杆受到转轴的弹力的大小始终为2mgsinθ

D.轻杆受到转轴的弹力的方向始终在变化

分析与解:当杆绕O点转过任一α角时，对于小球a、b及杆组成的系统，所受外力的合力矩即为a、b小球重力下滑分力对O点产生的力矩之和，显然a、b小球重力下滑分力对O点产生的力矩之和为零，即系统匀速转动。所以A、B错误。

对于C、D选项的判断，学生给出了以下三种解法：

方法一：矢量运算法

医院总务处进行的综合节能鱼骨图分析就展现了思考的细致程度。分析将综合节能划分为四大路径，分别是重点用能单元节能降耗、管理节能、可再生能源使用以及更换老旧设备、使用节能产品。

对于处于任意位置的a、b小球及杆组成的系统，由牛顿第二定律有：

即轻杆受到转轴的弹力的大小N=2mgsinθ，方向沿斜面向上。C选项正确。

方法二：非正交分解法

将a、b小球所受杆的弹力沿斜面方向和沿杆方向分解，如图，沿斜面方向的分力分别为Fa1、Fb1，沿杆方向的分力分别为Fa2、Fb2，即有：

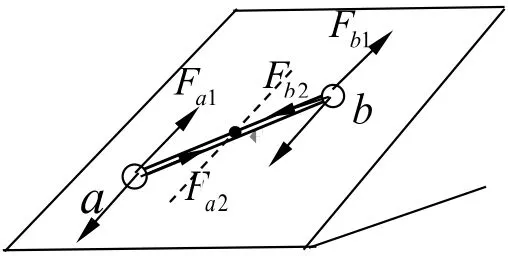
Fa1=Fb1=mgsinθ，Fa2=Fb2=mω02R

对轻杆受力分析如图，由牛顿第三定律：

Fa1′=Fa1=mgsinθ，Fb1′=Fb1=mgsinθ

Fa2′=Fa2=mω02R，Fb2′=Fb2=mω02R，沿杆向合力为零

则：N=Fa1′+Fb1′=2mgsinθ，方向沿斜面向上。C选项正确。

方法三：矢量图叠加法

设小球a、b的重力沿斜面方向的分力分别为Gax、Gbx，轻杆对球的作用力分Fa、Fb，

小球a、b在斜面内受力的矢量三角形如图（垂直于斜面俯视图）：

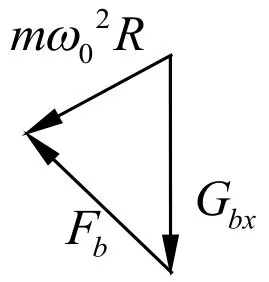
将两矢量图平移叠加可得杆对小球的作用力Fa、Fb的合力F=Gxa+Gxb=2mgsinθ，方向沿斜面向上。

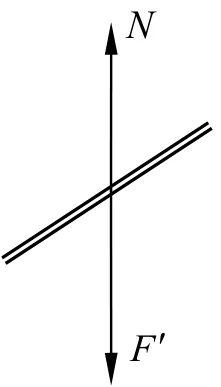
对轻杆有：N=F′，而F′=F=2mgsinθ

即轻杆受到转轴的弹力的大小N=2mgsinθ，方向沿斜面向上。C选项正确。

方法一避开了列繁琐的牛顿第二定律分量式方程组及解方程组的复杂过程，巧用矢量式方程，再利用，轻松解决问题，体现了物理规律大道至简的属性。

方法二跳出常用的正交分解法的梏桎，根据具体情况采用了非正交分解法，将杆对球的作用力沿斜面方向和沿杆方向分解，这种反常规的方法使问题迎刃而解。

方法三巧妙地将两个力的矢量三角形叠加，非常直观地得到杆对两球作用力合力的大小和方向，从而得到两球对杆的作用力是一恒力，这种新颖、独到的方法使问题拔云见日。

以上三种方法都体现了学生思维的创新性，对所学的基本知识和方法并不是机械地接受，而是进行了加工和创新，根据实际情况来解决问题，这也正是我们教育要达到的目的。

21世纪呼唤创新人才，而创新人才的培养关键是教育。教育要与时俱进，新课程改革要求高中物理教学要改变过去一味强调知识传承的倾向，要不断探索适合学生的教学，拓展学生的思维，提高学生的创新能力。在我们平时的教学中，我们应利用好教学的素材，采取多种教学方式，调动学生学习物理的兴趣与主动性，推陈出新，适时地去激发学生创新思维，培养学生的创新能力，为国家和社会培养创新型人才。