基于ESO 的随动负载模拟器控制策略
周生龙,陈机林,侯远龙,姜昭钰,史蒂芬
(南京理工大学机械工程学院,南京 210094)
0 引言
炮控系统的工作状态非常复杂,实际工作中会受到各种干扰力矩的影响,为满足炮控系统的高动态要求,检验其随动系统的性能,随动负载模拟器可作为研究其各项指标的平台。随动负载模拟器采用力矩电机实时输出力矩的方法模拟炮控随动系统在实际运行过程中承受的各种力矩载荷,并采用位置电机模拟该系统的方位和高低角度。但在实际运行过程中,一些不可避免的非线性干扰,如:摩擦和传动部件之间的齿轮间隙等,会影响随动负载模拟器电机的跟踪精度。因此,将现代化的控制策略应用于随动负载模拟器的研究之中,可以有效提高其动态响应精度,达到理想的效果。
牛国臣等为保证电动负载模拟器力矩精确加载,设计了基于迭代学习控制和舵机位置前馈补偿结合的复合力矩控制器,但主要用于具有周期性的正弦信号控制,响应速度和抗干扰能力较差。刘晓林等提出了以改进型基于信度分配的小脑模型关节控制器为前馈控制,以增量式比例积分微分为反馈控制的复合控制策略,该方法提高了系统的加载精度及在线实时控制能力,在一定程度上抑制了多余力矩干扰,但没有考虑摩擦等非线性因素带来的影响。马小勇等提出高阶非线性自适应终端滑模控制策略,避免了参数变化和扰动对系统的影响。将舵机看作一个扰动输入,确立负载模拟器系统为双输入单输出非线性系统,建立负载模拟器非线性数学模型,并基于此模型提出自适应终端滑模控制策略。分数阶滑模凭借其优异的性能,近年来被广泛应用于控制领域。文献[5-6]将分数阶滑模应用于各自的控制研究方向,取得了理想的效果,但分数阶滑模控制在负载模拟器方向上的应用还比较少。
以上文献都为炮控随动负载模拟器的控制研究提供了方法和思路,故研究提出基于扩展状态观测器(ESO)的小脑模型关节控制器分数阶滑模控制策略。采用ESO 来观测系统中的摩擦、间隙等非线性影响因素带来的干扰力矩,同时也可以将负载模拟器普遍存在的“多余力矩”观测出来。小脑模型关节控制器(CMAC)以其收敛速度快,模型简单等特点,被广泛应用于多个领域,故可以采用CMAC 作为前馈控制器,控制系统的相应输出。为了提高系统响应的快速性及动态的稳定性,采用分数阶滑模作为控制器,利用分数阶积分逐渐遗忘故去的特性设计滑模面,同时双幂次趋近律可以使系统快速无抖的收敛到滑模面上。
1 随动负载模拟器的组成与建模
1.1 系统的组成与原理
如图1 所示,随动负载模拟器可以分为两个子系统:模拟加载系统和炮控随动系统,用力矩电机对随动系统的位置电机进行模拟加载。由于力矩电机和位置电机是同轴连接的,当位置电机根据主控计算机的指令运动时,会带动力矩电机的运动,从而产生了被动式力矩“多余力矩”;而当力矩电机根据指令对位置电机进行模拟加载时,也会对位置电机所处的位置产生影响。在实际工作中,炮控随动系统的位置电机实际转动的角度θ和指令角度θ之间存在一定的对应关系,故可将θ看作是模拟加载系统的一个扰动输入项。因此,模拟加载系统存在两个输入:指令角度和位置电机的实际角度。
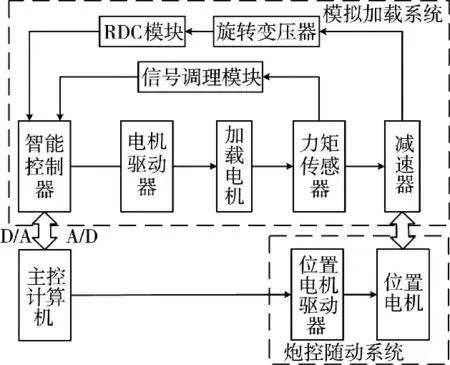
图1 随动负载模拟器的组成
1.2 模拟加载系统模型
研究采用永磁同步电机(PMSM)作为力矩加载电机,为了简化分析,假设PMSM 为理想化电机。PMSM 在同步旋转坐标系d-q 的模型为:

考虑随动负载模拟器中存在着摩擦、多余力矩等因素的影响,模拟加载系统的机械运动方程可为:

式(4)中,K为力矩传感器的刚度系数;θ加载电机转动的角度;θ位置电机转动的角度。
2 控制器的设计
2.1 扩展状态观测器的设计

2.2 分数阶滑模控制器设计


由式(20)可知,将双幂次趋近律加入控制律考虑后是满足条件的。因此,该分数阶滑模控制是稳定的,不论初始状态在任何位置,系统能从该状态到达滑模面。
2.3 非线性量化小脑模型关节控制器(cerebellar model articulation controller,CMAC)
CMAC 是一种运用查表法解决复杂非线性问题的技术,而并非是一种数值计算方法。其权值更新采用局部规则,相较于其他神经网络速度快。CMAC 收敛速度快,泛化能力强以及结构简单等优点,使其可以在负载模拟器的控制中合理利用。采用CMAC 来补偿滑模控制器的输出是一种较好的选择。
非线性量化结构,其计算过程与普通CMAC 神经网络的工作过程类似,主要包括量化输入,输入层到输出层之间的非线性映射和输出层权值更新学习算法。结构图如图2 所示。
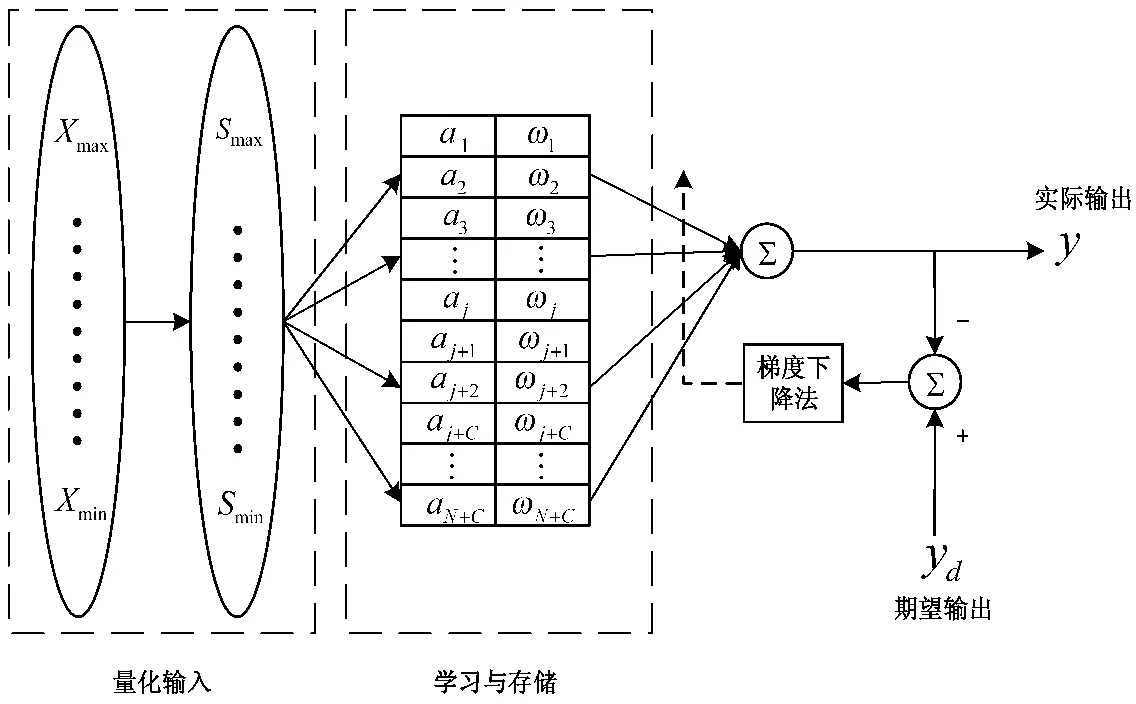
图2 CMAC 结构图
图中:X 为输入空间,S 为量化空间,A 为存储空间,a表示第j 个存储单元的激活情况,N 为量化级数,C 为泛化参数,ω表示第j个单元的权值。
常规的线性量化,如要达到较高的分辨率需要将量化级数增加至多倍,而非线性量化在满足分辨率的基础上,采用较小的量化级数。
由表1 可知,采用非线性量化仅需要在量化级数为100 时就可以达到分辨率为0.005。
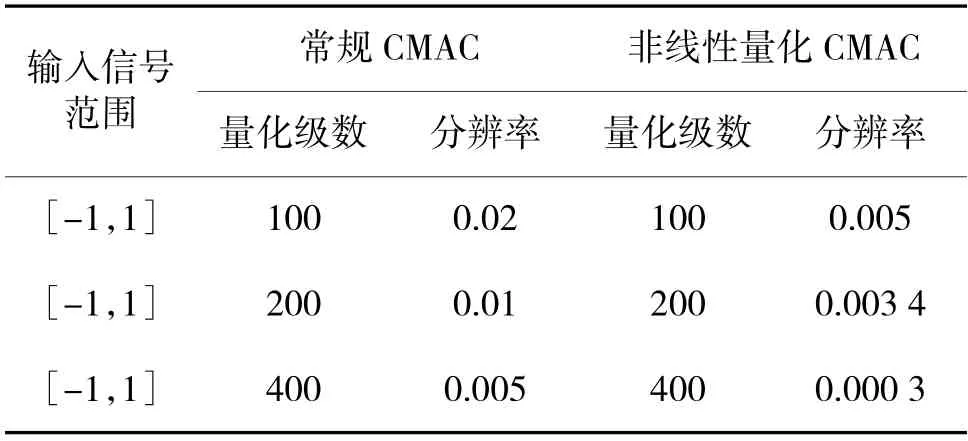
表1 CMAC 量化级数与分辨率关系


存储单元A 中的C 个单元将被激活,当输入变量X经过非线性量化变为S后,此时对应的输出为C 个单元的权值之和。
故输出为:



图3 加载系统伺服框图

3 仿真实验与分析
为了验证研究方法的可行性,分别进行了阶跃输入信号和正弦输入信号的仿真实验。并与普通滑模控制策略进行对比,得出了本研究方法的优越性。仿真实验中:
分数阶滑模控制器中参数选择如下:
k=10.533,k=0.168,r=0.167;
所采用的PMSM 参数如下:

表2 PMSM 参数
仿真实验结果图如图4 所示。
图4(a),(b)分别表示在0.1 s 时加入阶跃信号,普通的SMC 控制和本研(ESO-CMAC-SMC)控制对输入信号的响应的速度,以及误差大小。从误差图中可看出,在加载电机启动时,由于存在摩擦、间隙等非线性因素的影响,输出误差比较大;当指令加载10 N·m 的力矩值时,本研究策略的响应时间约为10 ms,伴随有0.35 N·m左右的超调,相对于普通SMC 的控制策略的3 N·m的超调量以及200 ms的稳态时间,可以认为达到了理想的效果。


图4 阶跃信号误差图
图5(a),(b)为加入幅值为10 N·m 正弦曲线信号时的仿真图形,从图中可以看出,启动时的误差每种的控制策略都相对来说较大,差值在5 N·m 左右;不过本研究策略经过学习过程之后,在25 ms 之后能始终跟随输入信号,误差近乎为零,幅值相差在2%以内,而普通SMC 控制策略则由于“抖动”的问题,无法将误差进一步缩小,幅值相差超过7%,并没有达到跟踪信号的要求。

图5 正弦信号误差图
综合阶跃信号与正弦信号的比较可知,研究策略优于普通的策略,其响应时间和稳态误差都可以达到理想的效果。
4 结论
研究在分析影响随动负载模拟器加载精度的基础上,设计了ESO 来估计系统中存在的未知干扰项;考虑分数阶滑模的优点,结合双幂次趋近律,将其设计为速度环控制器,控制效果的提升较为显著;最后借助于非线性量化的CMAC 前馈控制器,实时学习与更新参数,对于动态的误差补偿等作用良好,增强了系统的鲁棒性。经过仿真实验证明,本研究对随动负载模拟器的控制研究可以提供一定的借鉴与参考。

