基于Dijkstra 改进遗传算法的定向越野赛道设计*

欧丽珍，杨 旭，李新梦，罗雪山

（国防科技大学，长沙 410073）

0 引言

真实军事作战中，是否懂地形、能否充分发挥地形的作用是影响作战胜负的关键因素之一。军事地形学是军队院校必修课程之一，包含理论教学和实践教学两个部分，其中，军事地形学实践教学又称为军事定向越野或定向越野，其主要目的在于培养学员识图、用图以及军事标图等技能。因此，定向越野逐步成为了一项常态化的军事训练科目。

定向越野是一种利用指北针以及地图或地形图等指向工具，根据一定的比赛规则在野外行进至终点，最终得分高者获胜。定向越野路线设计是通过在合适的地图或地形图上设计起点、检查点以及终点，规划定向比赛过程，从而获得尽可能公正的赛道的过程。但在实际比赛中，往往只知道起点及检查候选点，在规划路径时，需要自行确定终点及必经检查点，其中，必经检查点是指所有赛道都经过的检查点，用于提供水以及医疗物资等。定向越野运动在军校学生的训练中具有重要意义，这项运动不仅考验参与者的体能、意志，同时也将考察识图技能、方向辨认等。定向越野比赛要求的空间较大，通常选择森林、公园、校园以及山地等，往往包含一些未知地理地形等，因此，这也将锻炼参赛选手应对突发情况的能力。

实现多路径定向越野比赛路径自动化设计有利于促进军事定向越野运动的发展，提升参与者自身的综合素质。目前关于越野赛道的研究集中于单路径最优，这对于多路径定向越野比赛并不适用，多路径定向越野赛道设计更加注重赛道之间的均衡，而非最短或是最优单路径，据此，构建多路径定向越野模型框架，有利于减少路径设计成本，促进定向越野运动发展。

1 背景介绍

多路径定向越野比赛通常安排若干条比赛赛道，所有路线的起点和终点相同，每条赛道可安排一个或多个选手，同一赛道的选手间隔一定时间出发，不同路线的首发参赛选手同时出发。良好的赛道设计需保证赛道的公平性及参赛选手的良好参赛体验。根据以往的赛道设计经验，结合实际需求，本文设计以下约束。

规则1：不同路径的长度尽可能均匀，为简化模型，通常假设参赛选手在各打卡点之间沿直线前进；

规则2：不同路径的总打卡难度尽可能均匀，打卡难度通常用完成该任务的平均时长代替；

规则3：不同路径的爬高量尽可能均匀，其中，爬高量是指若后一个打卡点的Z 坐标比前一打卡点高，则两者之间的差值称为爬高量；

规则4：避免包含较多的重复路段，即“尾随路段”，防止参赛选手之间有意或无意地相互交流与协助；相邻或相近检查点打卡顺序应当尽可能连续，且路线尽可能短；

规则5：路径检查点数量大于等于一个定值D，且通常包含d 个公共检查点；

规则6：同时抵达（时间间隔小于1 min）同一检查点的队伍数小于等于p，以保证参赛队伍良好的参赛体验感；

规则7：需保证参赛选手以平均速度v行进，参赛选手平均完成时间不小于t且不大于t，保证选手充分体验比赛且不至于过度消耗。

规则8：终点通常设立在任务难度较低的点。

其中，规则1～规则3 是为了保证各赛道尽可能均匀，减少赛道差异对比赛的影响，规则4～规则5 则是为了保障比赛的顺利进行；规则6～规则8 则是为了保证比赛选手的参与体验。

赛道基本类型包含闭合路线、半闭合路线、开放路线、交叉路线、星型路线1 以及星型路线2 共6种形式，如图1 所示。

图1 越野赛道基本路线类型

因此，若需设计闭合路线，则终点的候选集应当包含起点。

2 模型建立

约束4：规则4 要求避免包含较多重复路段，且同一路线中打卡顺序应尽可能连续，路线长度尽可能短。

重复路径表示在两个最短路径序列中，两个相同节点相邻出现，因本题路径为相同起点和相同终点，因此，不考虑逆向路径的可能，即不考虑两条路径同时存在节点A →节点B 和节点B→节点A 的情况。据此我们构建一个新的路径序列矩阵M。

综上所述，多路径规划的目标为各路径长度、难度以及爬高量的方差尽可能小。其中，约束1～约束3 将用于路径初始化及后续生成；约束4～约束6主要用于挑选合适路径。

3 Dijkstra 改进遗传算法基本原理

3.1 模型介绍

遗传算法（genetic algorithm，GA）具有鲁棒性、适应能力强等优点。近年来，遗传算法已成功应用于工业、金融以及交通运输等领域，在路径优化领域取得了较大发展，因此，本文选用遗传算法对模型进行求解。但传统的遗传算法仅能获取一组无序的节点序列，而无法给出最短路径。Dijkstra算法是图论中求最短路径的著名算法，本质上为贪心算法的实现，目的是寻找起点到各点距离获取最短路径。因此，可以利用Dijkstra 算法对遗传算法的结果进行最短路径排序。

基于Dijkstra 改进遗传算法包括8 个步骤：1）编码；2）初始化种群；3）利用Dijkstra 算法对种群进行排序；4）对种群个体适应度进行评估；5）按照优胜劣汰和适者生存的原理选择个体；6）模拟自然遗传学进行染色体交叉和变异；7）Dijkstra 算法对新产生的种群进行修正、评估；8）逐步迭代，直至满足停止条件，求取最终解。基本流程如图2 所示。

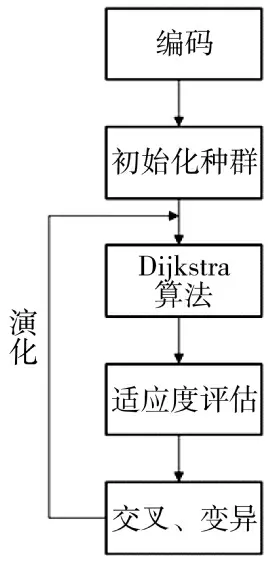
图2 Dijkstra 改进遗传算法流程

3.2 模型相关设定

3.2.1 编码

编码是指DNA 中遗传信息在一个长链上按一定的模式排列，即可以看成表现型到基因型的映射。遗传算法的编码主要包括二进制编码、格雷码编码、实数编码、符号编码4 种。其中，二进制编码具有操作简单，容易计算等优势，因而常被采用。

3.2.2 初始化种群

随机生成由n 个个体组成的种群，即可行解集合，通过模拟优胜劣汰的自然法则对这些种群进行重新选择，获取优秀的种群及个体。

3.2.3 最短路径获取

在多路径规划问题求解中，依据约束1～约束3初始化种群后，需经过Dijkstra 算法对各节点进行排序以获取最短路径。

3.2.4 适应度函数选择

适应度函数通常是用于区分种群中个体好坏的标准，在多路径优化算法中，可以选用约束4～约束6 进行选择，计算方便快捷，同时不会出现由于异常个体或者差异不大的个体造成选择结果不理想的状况。

3.2.5 交叉和变异

交叉是指在遗传学中，父母双方的基因可能在某一个位置相互交换；变异则是模拟生物进化过程中小概率基因突变事件。通过交叉和变异产生新的个体（调整节点顺序），重新进行评价、选择、杂交和变异，直至抵达终止条件。终止条件由目标函数确定。

3.3 场景需求与模型应用

1）若路径条数为定值，则直接输入N 的值即可。

2）调整约束4～约束6 可以适应不同的场景，若无相关需求，则可删除相应的约束；若模型无可行解，可自行调整参数p，t，t的数值。

3）若路径条数未知，但希望赛道容纳尽可能多的人，则可增加一个目标函数，即在满足约束的前提下，让路径数量尽可能多。

4）若无法获取高程数据（Z 坐标值）、或是高程数据差异较小（如平原等），则去掉约束3，将长度改为二维欧式距离公式计算即可。

5）若需对参赛选手进行分配安排，则可通过增加关于选手的约束即可，模型整体框架不变。

4 实验分析

为验证模型的可行性，本文采用一次真实定向越野比赛数据进行验证分析。

模型目标函数为容纳尽可能多的参赛选手，其中，p=5，t=2，t=3，v=6。其中，各节点难度值w={1，2，3，4}，最终试验结果如表1 所示。从表1 可知，路径条数为6 时，难度方差、长度方差、爬坡方差以及完成时间方差综合较小，且人数相对较多。

表1 试验结果展示（部分）

图3 数据概览（红色△表示起点，红色×表示低难度节点，即终点候选集，中间节点用灰色○表示）

5 结论

本文利用基于Dijkstra 改进遗传算法对模型进行求解，并利用实际数据进行验证。结果表明，本文提出的多路径多目标规划模型可以通过不同的参数设定和约束调整，满足多种场景需求，具有广阔的应用前景。同时，多路径多目标规划模型可应用于多静点多路径探查任务，如侦察任务等。