基于复合控制的舰载火箭炮伺服系统仿真

李方舟，郝巨东，李 丽，梁海峰，李 阳

（北方自动控制技术研究所，太原 030006）

0 引言

和平与发展是当今世界的主旋律，可是近年来我国周边形势发生着深刻而复杂的变化。我国在东海、南海、黄海与周边国家的海洋争端日益突出，都表明海上冲突现已成为世界各国争端的主要表现形式，为维护国家领土完整、海洋权益和人民的财产安全，我国海军越来越重视海军力量的建设。随着我国海军现代化建设进程的加快，舰载武器系统的研究已成为一个十分重要的课题。舰载火箭炮是常见的舰载武器系统之一，舰载火箭炮具有发射速度快、火力强、覆盖面广等特点，已成为现代战争中主要的火力压制和支援武器。所以，舰载火箭炮对伺服系统控制快速性、稳定性具有更高要求。

目前，为了提升舰载武器伺服系统控制性能，相关学者对其进行了研究。金鹏程等提出了采用RBF 神经网络PID 与模糊控制相结合的策略，根据误差大小，两种控制方法在不同区段间切换；项军等学者设计了位置和速度复合控制的滑膜控制器，并利用RBF 神经网络获得控制器中不确定参数，以提高系统对扰动的响应速度和控制精度。改进后的控制方法虽然提高了舰载武器伺服系统的控制性能，但控制信号量总是滞后于系统受到的实时扰动，在随机的持续扰动下往往难以产生较好的控制效果。

海面波浪极为复杂，它是不规则的随机波。海浪形成的原因有多种，如风、海啸和潮汐都可以引起海浪。海浪往往随着风的作用向各个方向传播，形成大小形状不等的丘状波面。其波倾角可看作是非线性的随机序列，在对非线性随机序列的预测研究中，门控循环网络（gated recurrent unit，GRU）相较于BP 神经网络、RNN 循环神经网络、长短期记忆网络具有精度更高的优势，赵建鹏将其应用在位置预测控制方法中，抑制海浪产生的持续扰动对舰载稳定平台产生的影响。

20 世纪韩京清教授提出并由高志强教授简化改进的线性自抗扰控制（linearactive disturbance rejection control，LADRC）将被控对象运动过程中产生的参数变化等不确定因素视为“未知扰动”，通过线性状态观测器（LESO）利用输入输出信息实时估计补偿。LADRC 不依赖被控对象精确的数学模型，在控制过程中具有很强的鲁棒性。目前，对线性自抗扰控制的应用和研究涉及了众多领域，如电力系统、工业控制系统、航天伺服系统，都取得了较好的控制效果。

为了进一步提高和改善舰载武器伺服系统鲁棒性及跟踪性能，本文将二阶线性自抗扰控制器取代原有伺服系统中速度-电流控制闭环，提升电机对负载扰动、工况变化下的适应性能。而位置环采用基于门控循环网络预测的PD 控制，门控循环网络根据海浪过去状态对位置输入进行预测补偿，提高系统对海上风浪等持续扰动的方位保持性能。

1 被控对象建模

目前某型火箭炮方位伺服系统采用交流永磁同步电机驱动，俯仰伺服系统采用泵控液压驱动伺服。本文以方位伺服采用的交流永磁同步电机作为研究对象，忽略铁芯饱和、涡流和磁滞损耗等因素，建立矢量控制模型，采用i=0 的控制策略，并将PWM 逆变器等效为时间常数为T的一阶惯性环节，将电压方程简化得到系统i与u、T与i、ω与T间的传递函数：

根据式（1）建立如图1 所示的被控对象模型。

图1 中，i为q 轴电枢电流；L 为电枢电感，L=L=L；R 为电枢绕组电阻；s 为拉普拉斯算子；K为反电动势系数；K为转矩系数；T和T为电机电磁转矩和负载转矩；J 和B 为折算后的电机负载转动惯量及粘滞摩擦系数；ω为电机输出转速，受控对象永磁同步电机模型中各参数值如表1 所示。

表1 PMSM 模型参数

图1 被控对象模型

2 控制原理及模型构建

2.1 线性自抗扰控制原理

线性自抗扰控制假定被控对象的模型为

构造模型辅助线性扩张状态观测器（LESO）来估计系统状态和“总扰动”：

L为LESO 增益：

当A-LC渐进稳定时，z趋近于输出y 及y 的各介导数，z趋近于扰动f，取如下控制率：

线性自抗扰控制器可由如下状态空间方程实现，结构如图2 所示。

图2 LADRC 控制结构

线性自抗扰控制需整定的参数为LESO 的增益L和状态反馈控制增益K。K中的b取值应尽量逼近系统的实际高频增益b，通常b越小，控制作用越强，但稳定裕度越小。

对于LADRC 参数整定方法主要有：带宽法、基于内膜控制器的参数整定方法、基于高阶控制器的参数调整方法等。对于L及K的取值，高志强教授提出带宽整定法是将L中的β及K中k的整定转化为两个参数的整定：观测器带宽ω及控制器带宽ω，此时

2.2 门控循环网络（GRU）

GRU 作为长短期记忆网络（LSTM）结构简化的变体，其前向传播公式如式（12）所示：

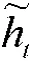
2.3 模型构建

对于第2 节建立的火箭炮伺服系统中被控对象，其传递函数可视为二阶被控对象。本文设计二阶线性自抗扰LADRC 控制器控制火箭炮伺服系统电流环、速度环及位置环，采用门控循环网络预测补偿的PD 控制。设计LADRC 中二阶线性状态观测器观测PMSM 的电流和转速输出，n 取2 时，由式（4）得二阶LESO 状态方程如式（13）所示，控制律u方程如式（14）所示。

根据随机海浪理论，选择P-M 谱作为海浪谱密度函数，建立三级海况下的longuet-Higgins 海浪模型。仿真过程中取有义波高1.25m，仿真频段0.3 rad/s～3.0 rad/s，频率增量0.09 rad/s，参考文献［14］中构建的船舶横摇角φ 与波倾角α 间的传递函数式（15）。仿真得到海浪引起的扰动曲线如图3 所示，将其等效为伺服系统受到的位置扰动。

图3 海浪扰动仿真

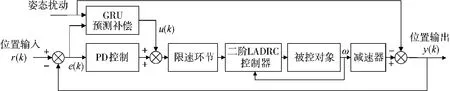
图4 基于门控循环网络预测的PD+LADRC 结构图

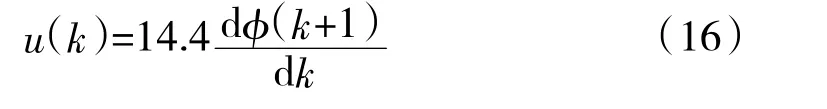
3 仿真分析

对PID 控制、基于GRU 的PID 控制和基于GRU 的PD+LADRC 方法的舰载火箭炮调炮控制进行仿真比较。仿真过程将海浪扰动对炮管摆幅的影响简化为其对伺服系统位置输出的直接影响。基于门控循环网络预测的PD+LADRC 控制火箭炮伺服系统仿真如图5 所示。

图5 基于门控循环网络预测的PD+LADRC 控制仿真

速度- 电流环采用PID 控制器闭环控制的对照对象速度环和电流环控制率分别为8+2/s、10+0.053 1/s。二者位置环采用相同的PD 控制率210.2+20.3 s，s 为拉普拉斯算子。仿真给定调炮高低阶跃输入500 mil，负载转矩为d=（20 sint+100）N·m，单位变换与减速比的乘积为0.66，限速环节限制转速3 000 r/m。

在无海浪扰动时，两种控制方法调炮仿真结果如图6 所示。在达到500 mil 时二者均无超调，PID 控制的调节时间为3.2 s，稳态误差为1.1 mil；PD+LADRC 控制下调节时间为2.6 s，稳态误差为0.15 mil。可以看出，LADRC 对转速的跟踪控制有效降低了负载扰动对稳态误差的影响，减少了调炮调节时间。

图6 无海浪扰动下调炮仿真

在三级海况扰动下的仿真结果如图7～图8 所示，不加入GRU 前馈补偿且在PID 控制下，火箭炮位置输出在接近给定位置±8 mil 的范围内大幅摆动，无法维持稳定。加入GRU 补偿后，在PID 控制下稳定误差保持在3.1 mil 以内；而在基于GRU 的PD+LADRC 控制下，稳定误差保持在0.8 mil 以内。

图7 海浪扰动下调炮仿真

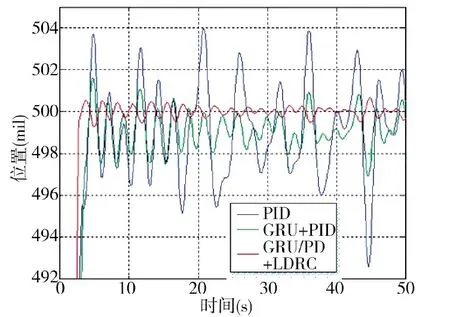
图8 海浪扰动下稳态对比曲线

4 结论

本文将门控循环网络预测理论、线性自抗扰与传统PID 控制相结合，用于舰载火箭炮方位伺服控制仿真中。线性自抗扰的引入使电机的控制性能得到提升，电机转速迅速跟踪位置环给出的控制量，缩短了调炮调节时间并降低了稳态误差；GRU 位置预测补偿的方法减少了海浪扰动对系统的影响，有效提高了在复杂环境下的鲁棒性、实时性。二者相结合达到了较好的控制效果，对于我国火箭炮控制性能的提高有一定的现实意义。