主成分分析和聚类在器材采购优先级制定中的应用*

刘 畅，肖 斌，伍 洁，张东东，蒋铁军

（1.海军工程大学，武汉 430033；2.武警第二机动总队，福州 350200）

0 引言

车辆装备既承担着人员、物资、武器装备的运输任务，又肩负着主战装备的机动任务。目前全军现有近300 种车型（含专用车型），涵盖了一、二、三代车型，每种车型由上万种零部件组成，消耗量巨大，规律复杂，因此，难以对每一类器材进行有针对性的预测。库存器材的采购优先级分类是根据采购优先级程度对需要重点管理或只需一般管理的器材进行分类，并实施不同的管控策略，实现差异化的库存管理。

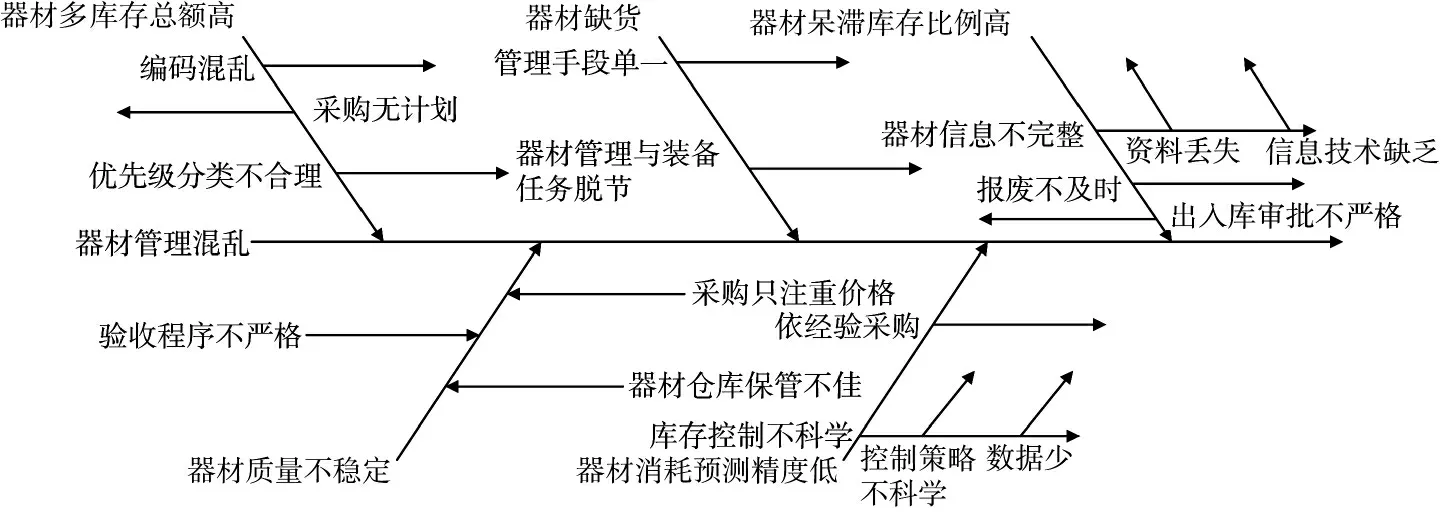
图1 器材管理问题鱼骨分析图

本文对器材采购优先级分类开展研究，一是合理划分库存类别。综合考虑多种因素，建立器材评价指标体系，利用主成分聚类改善现有分类界面不清楚、分类结果模糊的问题。二是实现库存成本最小化。在划分为不同的优先层级的基础上，针对不同层级，实施不同的库存模型，以减轻库存积压现状，降低经费成本，提高保障效率。

1 研究现状

常用的分类方法有ABC、SBC、VED、CVA、FSN、Kraljic、AHP-ABC、聚类、SVM 分类法。VIFREDO P 提出ABC 分类法。文献［4］按重要性、釆购周期的程度，结合不同的属性分成ABC 3 类。文献［5］提出了开发出一套能根据失效率动态确定关键备件系统的ABC 分类法。文献［6］提出了以减少故障排除时间为目标维修中的备件重要性为标准的分类方法；文献［7］结合设备关键性与供应因素对备件进行分类，制定了各类别的需求预测和订货模型。文献［8］将ABC 和CVA 相结合，降低了备件库存的数量和种类，进而降低了库房占用的概率。文献［9］针对备件的功能、存储条件、经济性、流通速度、技术关键度，定性定量相结合，采用多指标模糊评判法进行分类，按照需求特性、消耗特性和性能参数分为连续需求ABC 类、间歇需求ABC 类。文献［10］基于备件流速分类的基础上采取AHP 对ABC进行改进。文献［11］将备件分为不可预测和可预测备件，将可预测备件划分3 个等级，提出了相应的库存控制模型。文献［12］在ABC 的基础上提出了依工期特点对设备分类，在设备分类的基础上再对备件分类。

2 采购优先级评价指标体系设计

采购优先级分类指标包括单价、寿命、采购周期、消耗量、消耗额、关键性、储存要求、来源、供应风险、采购提前期、需求间隔、需求波动等。文献［1］选取单价、消耗量、采购提前期、关键性、需求间隔作为备件的库存分类指标。文献［13］选取消耗额、库存成本、采购提前期、需求波动系数作为库存分类指标。文献［14］选取需求时间、需求数量、供应风险和重要程度为分类指标。经综合军事院校、部队及工业部门9 名专家意见，从经济性、消耗性、重要性、难易性4 个方面进行设计，如图2 所示。

图2 器材采购优先级评价模型

3 改进的小样本聚类分析算法

聚类算法众多，可根据数据类型和目的加以选择，但没有一种方法适用任何聚类问题。其中，划分聚类作为应用最广泛的聚类算法，不仅适用于中小规模数据的聚类，同时对不同的问题都有较强的适应性。因此，本文选取划分聚类的方式进行聚类。对采购优先级别划分时，涉及的具体数较少，随意剔除数据会对结果造成影响。针对这一情况，本文设计了一种基于小样本的改进k-means 算法，以实际对象为聚类中心，减少了离群点的影响，同时，采取主成分对原始指标降维，降低了算法复杂度。

3.1 类别数k 的确定

K-means 的类别数无法事先给定，而肘方法根据所有对象的误差平方和确定k。当k 小于真实类别数时，增加k 将大大减少平方误差；当k 达到真实类别数时，聚类质量将随着k 的增加而迅速下降，这将导致每个对象的平方误差和减小的速度减慢。图像形似手肘，肘部对应的k 值即真实类别数。

3.2 确定高质量的聚类中心

K-means 的初始聚类中心为每类的中心。基于此，选择k 个不同密集域、远离初始中心的样本。过程为：取方差最小的样本为第1 类的初始中心，作圆。圆外方差最小的样本依次为下一类的初始中心，找完k 个初始中心。

3.3 改进聚类中心的重新选择

新的聚类中心定义为与其他对象距离和最小的对象。

实验平台为Intel（R）Core（TM）i7-9750H CPU@2.60 GHz，RAM16 G，Windows 7 操作系统，选用Matlab R2019a 作为编程工具。选取UCI 数据库的小样本数据集进行测试，UCI 数据库是加州大学欧文分校提出的用于机器学习的数据库，目前共有335个数据集，其数目还在不断增加，是常用的机器学习标准测试数据集，其中的wine，iris 常用于聚类和分类测试。Iris 也称鸢尾花卉数据集，包含150 个数据样本，分为3 类，每个数据包含4 个属性，4 个属性可预测鸢尾花卉属于哪一类。Wine 数据集是经典的葡萄酒数据集，包含来自3 种不同起源的葡萄酒的共178 条记录（178 种葡萄酒），13 个属性是葡萄酒的13 种化学成分，通过化学分析可推断葡萄酒的起源。

在iris 数据集、wine 数据集中各添加一项异常数据后，保持聚类类别数不变。

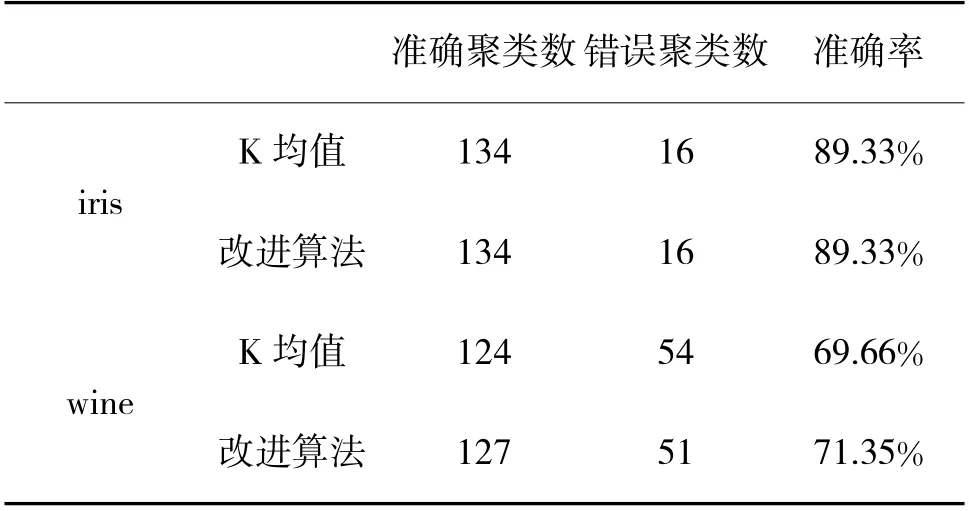
表1 两种算法聚类准确率对照（1）

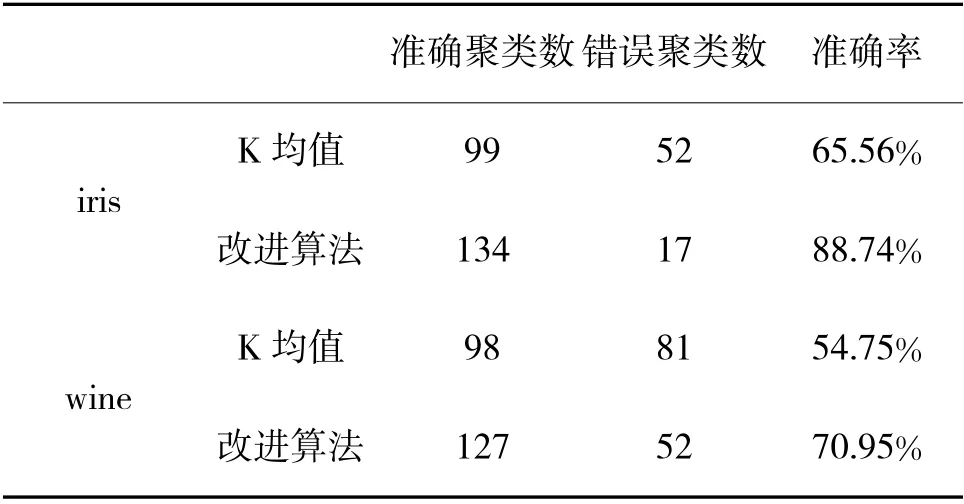
表2 两种算法聚类准确率对照（2）

从测试结果看，编写的程序较好地完成了数据的聚类任务，并且在保持聚类类别数不变时，添加异常数据对聚类结果无较大影响。

4 采购优先级分类步骤及模型

4.1 数据的收集与预处理

选取器材单价、平均库存量、占用资金、市场供货量、入库量、订货次数、出货量、采购提前期、采购费用、缺货损失为原始指标变量。个数为n，原始指标变量数为p，构建对象矩阵：

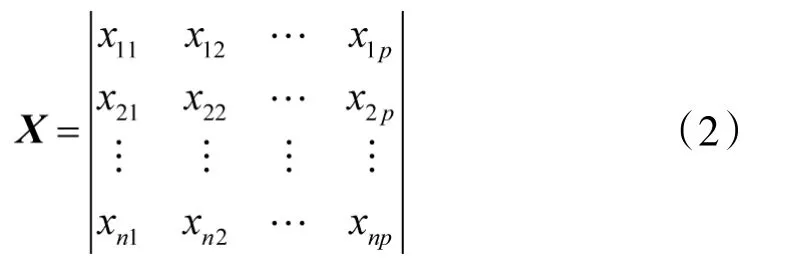
关于标准化，由于不需要标准化后的数据在特定区间内，并且各对象之间的数据可能相差较大，因此，采用Z-score 标准化。其转化函数为：

采用SPSS 计算数据的KOM 统计量，判断是否适用主成分分析。

4.2 主成分提取

接下来从选取的原始聚类指标中提取主成分，在减少聚类指标个数的同时不丢失原始数据的绝大部分信息。基本步骤如下：

1）计算各原始聚类指标的相关矩阵R

其中，指标x与x的相关系数r定义为：

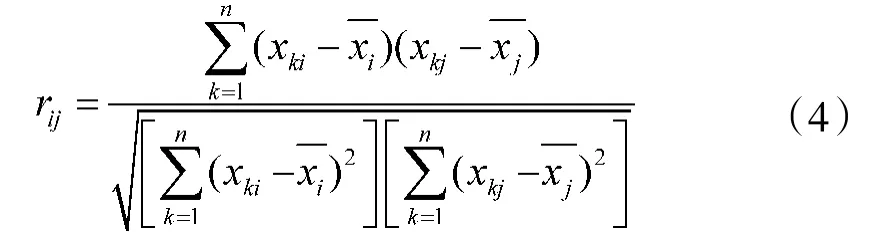
2）计算各指标对应的特征值及方差贡献率

计算所有聚类指标对应的特征值（λ，λ，…，λ）及对应的特征向量a=（a，a，…，a）。各个特征值对应的特征向量为构成各主成分的原指标变量线性组合的系数。各主成分的方差贡献率由对应的特征值除以全部特征值的总和得到。主成分总分由各主成分得分乘方差贡献率得到。

3）提取m 个主成分

将主成分按方差贡献率排序，前m 个的主成分累积贡献率大于85%表示其反映了原始数据的绝大部分信息。另外，在提取出重要的主成分后，应做好含义解释，赋予新的意义。具体做法是分析表达式中各原始指标前的系数大小，系数绝对值大的代表主成分反映该原始指标的信息较多。

4.3 改进聚类算法

计算各器材的主成分得分，以提取的m 个主成分作为聚类指标，根据改进聚类分析算法将器材划分成k 类。

假设器材数为n，主成分数为m，则聚类的对象矩阵为：其中，f表示各器材的主成分得分，由各器材原始指标变量值乘以相应的线性组合系数得到。

接着进行聚类，并计算聚类后的DB 指数，越小说明同簇内紧密，不同簇较远，聚类质量较高。

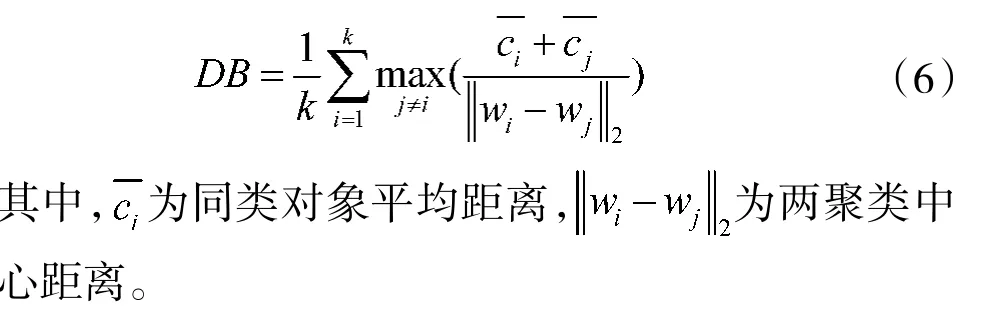
5 实例分析

以某型车辆器材合成数据为例，按照原始指标的选取原则，选取器材属性中的单价、平均库存量、占用资金、入库量、订货次数、出货量、提前期、采购成本、缺货损失、维修成本、保管成本、需求间隔、需求波动、在装量作为原始指标变量，查找相关文献，以19 种器材为分析对象，具体数据展示如表3 所示（已作Z-score 标准化，保留3 位小数）。

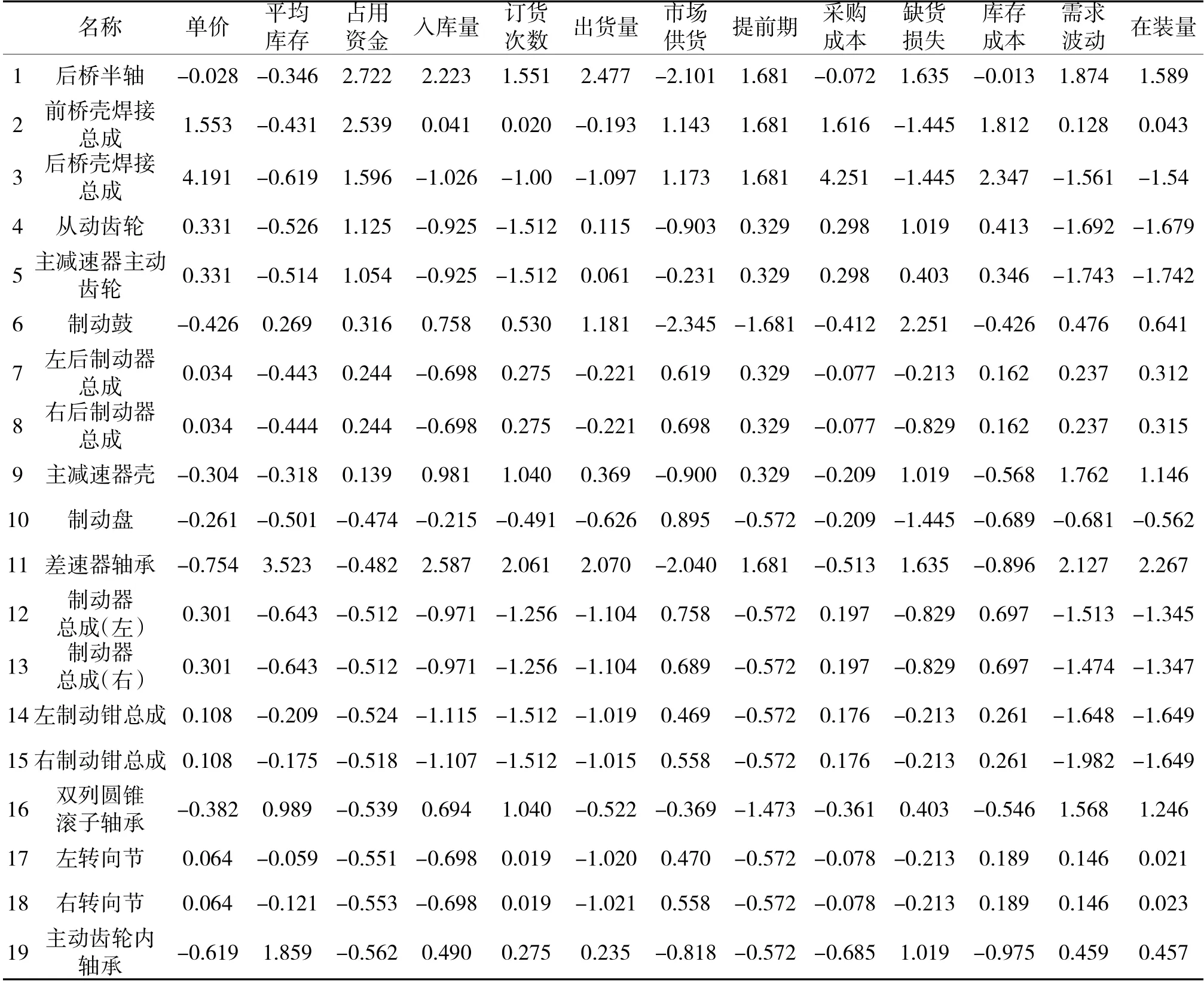
表3 器材采购合成数据

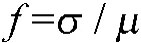
5.1 对数据标准化处理及因子分析适用性检验

将原始数据Z-score 处理，利用SPSS 21.0 软件通过KOM 检验和Bartlett 球体检验进行因子分析的适用性检验。KMO 值为0.644＞0.5，指标间存在一定的相关性。Bartlett 球体检验结果为250.472，Sig值为0.000，拒绝相关系数是单位阵，指标间相关。各变量的相关矩阵R 如表4 所示。

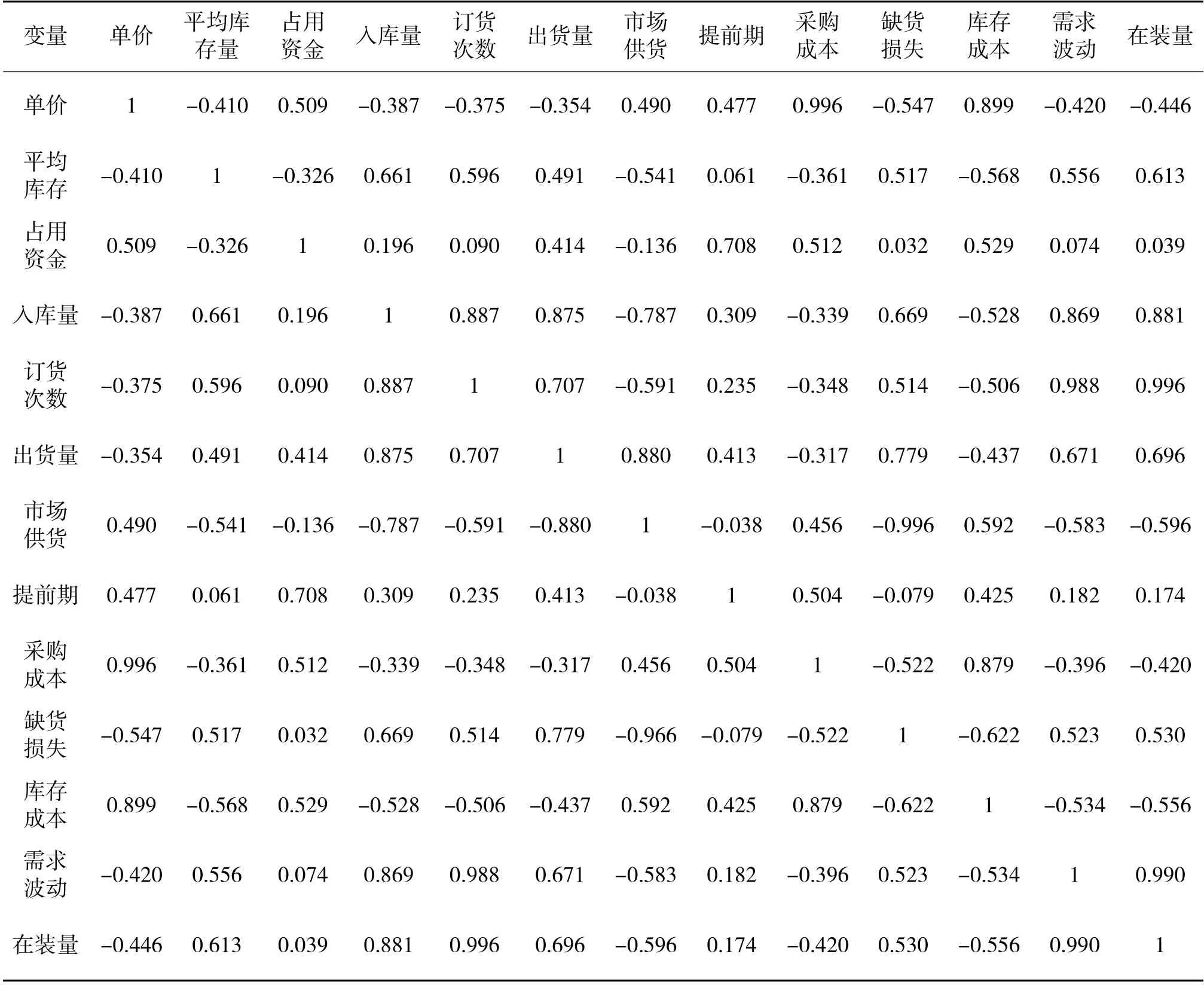
表4 相关矩阵R

各变量与自己相关系数都为1，表示自己与自己相关性最强；采购订单成本与单价、保管成本相关系数都大于0.8，说明它们的相关性较强，存在信息上的重叠；订货次数与需求波动、在装量相关系数都大于0.9，表示存在较显著的关系。

5.2 主成分分析过程

5.2.1 从相关矩阵出发求解主成分

由表5、下页图3 可知，前3 个主成分解释了全部方差的88.826%，说明提取的3 个主成分能够代表原来13 个器材采购信息的88.826%，所提取的主成分评价器材采购优先等级已有一定的把握。因此，提取3 个主成分，分别为Y，Y，Y，能够表示原始数据的绝大部分信息。

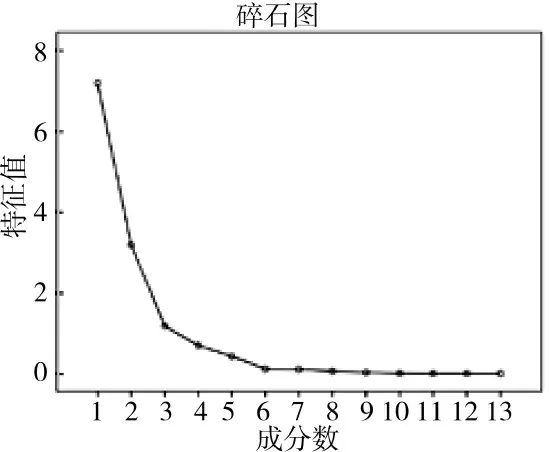
图3 主成分分析碎石图

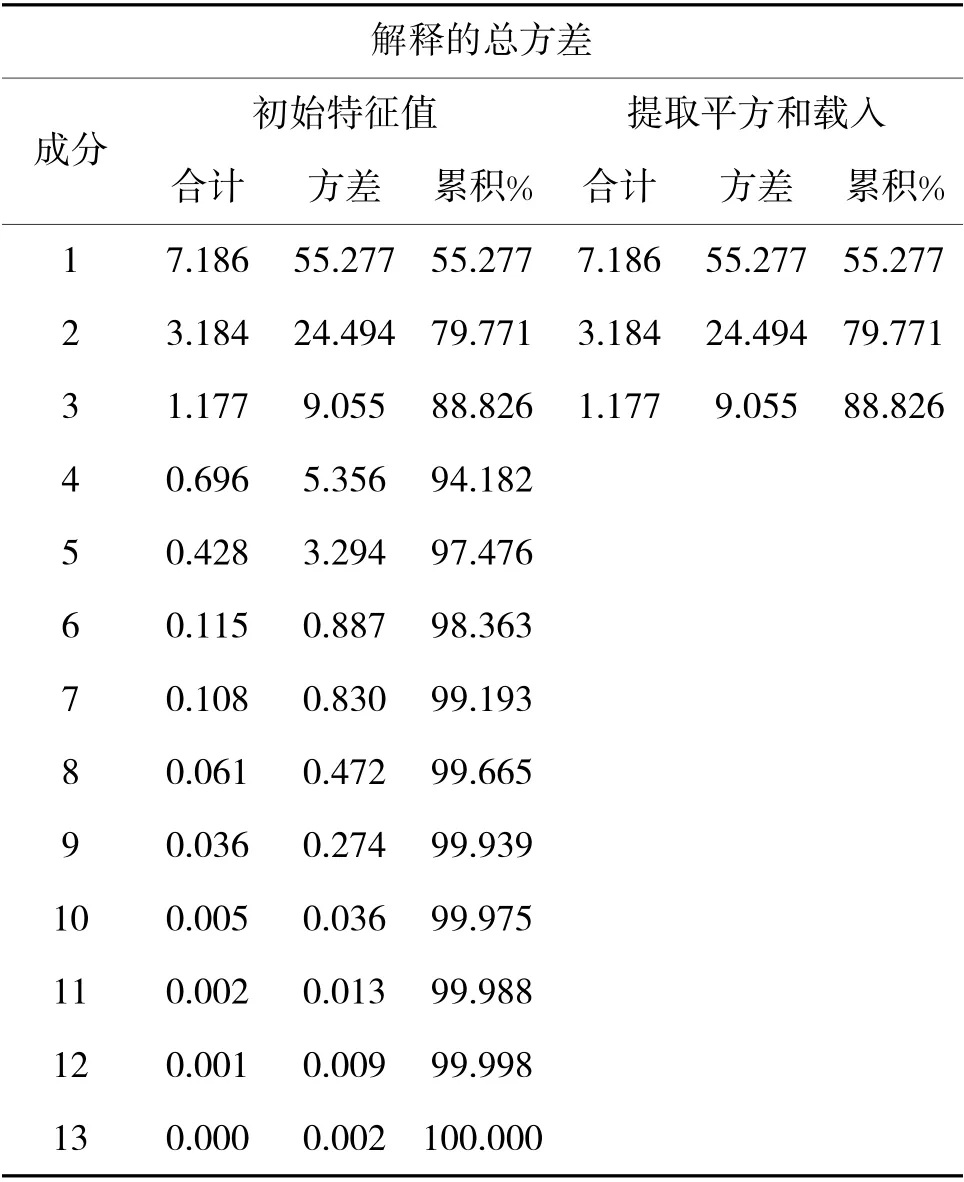
表5 主成分结果

5.2.2 计算主成分系数

选取主成分F、F、F为聚类指标。利用SPSS 求得成分矩阵，如表6 所示。

表6 成分矩阵

由图4 可以看出，主成分1 主要由入库量、平均库存量、出货量、订购次数、缺货成本、需求波动、在装量决定，这些因素高，主成分1 就越大，主成分1 代表了器材的需求程度。主成分2 主要由单价、占用资金、采购成本、库存成本决定，即主成分2 代表了器材的经济程度。主成分3 主要由市场供应量、在装量、需求波动、订货次数决定，即主成分3 代表了器材的采购难易程度。3 个主成分与器材采购优先级都是正向关系，因此，器材的主成分总得分能代表器材采购优先级大小。

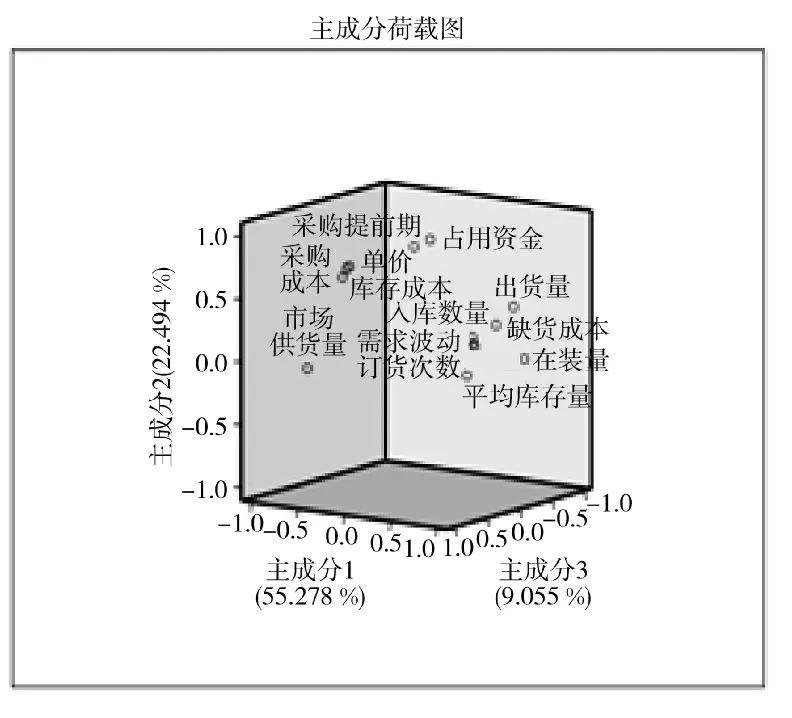
图4 主成分分析载荷图

主成分系数为成分矩阵除以对应特征值的平方根，代表各原始聚类指标在主成分中的比重（保留3 小数）如表7 所示。

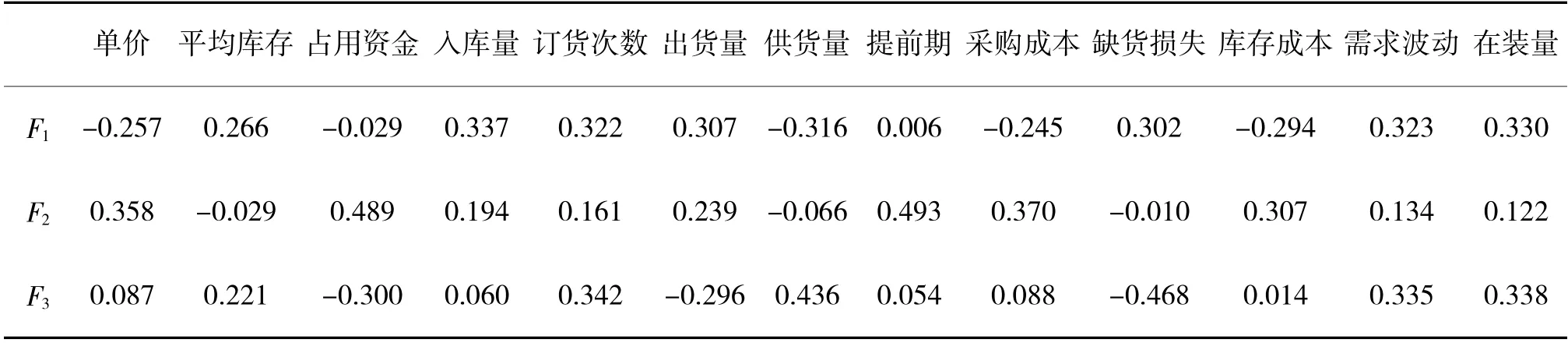
表7 主成分系数

将主成分系数与原始数据各变量值相乘，求得所有器材的各主成分得分（保留3 位小数，保留小数带来的误差在同一类器材中弥补）。以主成分方差贡献率占现有方差贡献率总和的比为权重，求得各主成分得分的加权和，得到各器材的主成分总分。按照主成分总分对器材排序。结果如下页表8 所示。

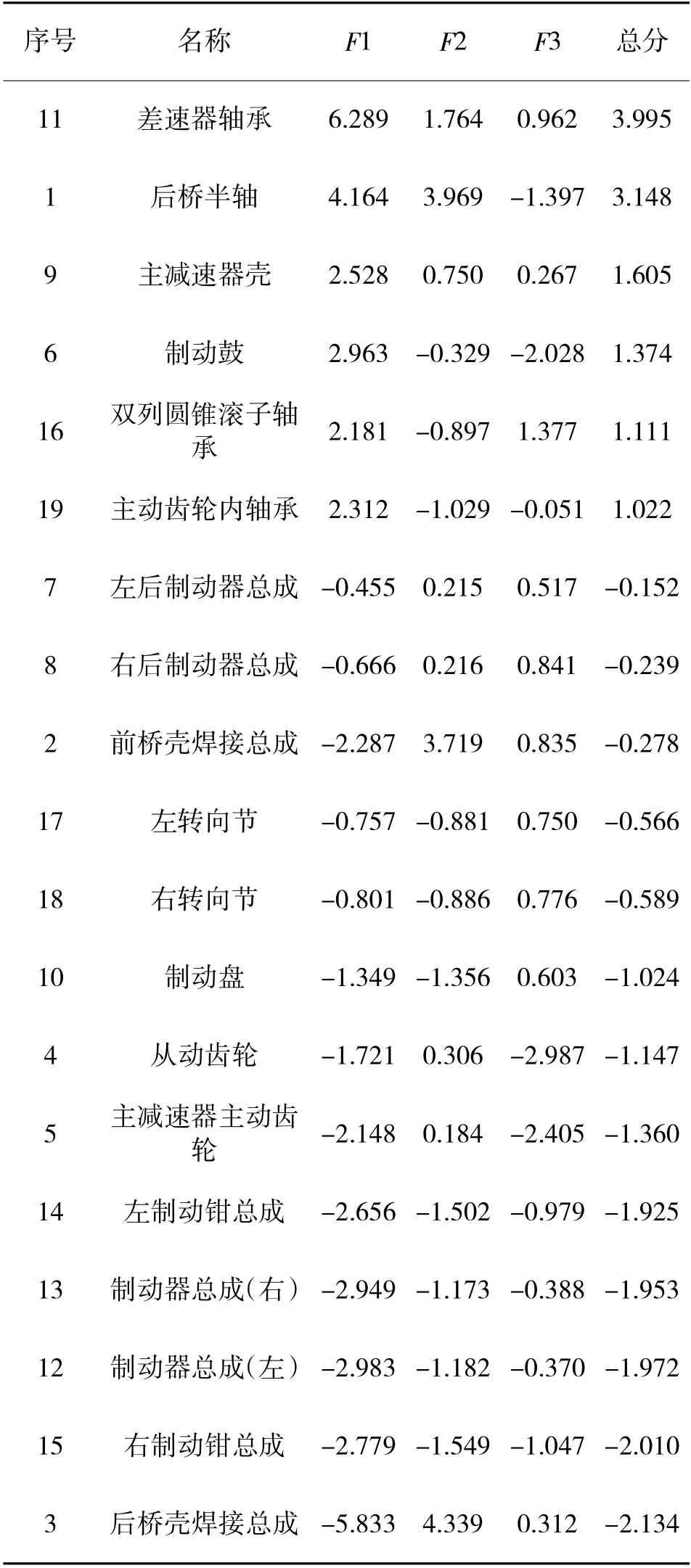
表8 各器材主成分得分

以主成分F、F、F为聚类指标，应用改进k-means 算法。计算不同k 值对应的误差平方和。根据肘方法类别数为4，按主成分平均总得分排序后结果如表9 所示。

使用k-means 同样将器材分为4 类，DB 指数为0.268，大于改进算法对应的值0.152，表明改进k-means 的聚类效果更好，更适用于本案例。

以主成分F、F、F为聚类指标，应用k-means、改进k-means 聚类，结果如表9、表10 所示。可以明显看出，分类差别主要在第二、三类。聚类分析结果。根据车辆装备器材管理特点，左制动钳总成、右制动钳总成和从动齿轮、主减速器主动齿轮、制动鼓的特点更加相似，因此，将其归为同类更加合理。左后制动器总成、右后制动器总成、主减速器壳、制动盘、制动器总成（左）、制动器总成（右）、双列圆锥滚子轴承、左转向节、右转向节、主动齿轮内轴承整体相对从动齿轮、主减速器主动齿轮、制动鼓而言在实际采购管理中更为重要，因此，改进k-means效果较聚类更为理想。主成分得分大的器材采购优先级较高，因此，第一类器材适用于最高等级的采购保障标准，后面类别的器材标准以此递减，19 个器材共划分为4 级。

表9 改进k-means 聚类结果

表10 k-means 聚类结果

5.3 采购优先级分类的库存控制策略

库存控制策略有（Q，R）策略、（R，S）策略、（t，S）策略、（t，R，S）策略和（S-1，S）策略5 种。

表11 器材库存控制策略

一类器材有后桥半轴和差速器轴承等。此类器材具有单位成本低、周转率快、订购次数高、需求波动大、在装量大、消耗量大、缺货成本高、采购难度大等特点。需要保持较高的库存服务水平，避免发生缺货情况。对于此类器材建议进行连续库存检查，每天更新库存状态，实时记录准确的库存信息。因此，选择（Q，R）连续型库存管理方法对二类器材做好管理。对库存储备连续检查，当库存水平低至R，则做好补货，订货量为固定值Q，如图5 所示。

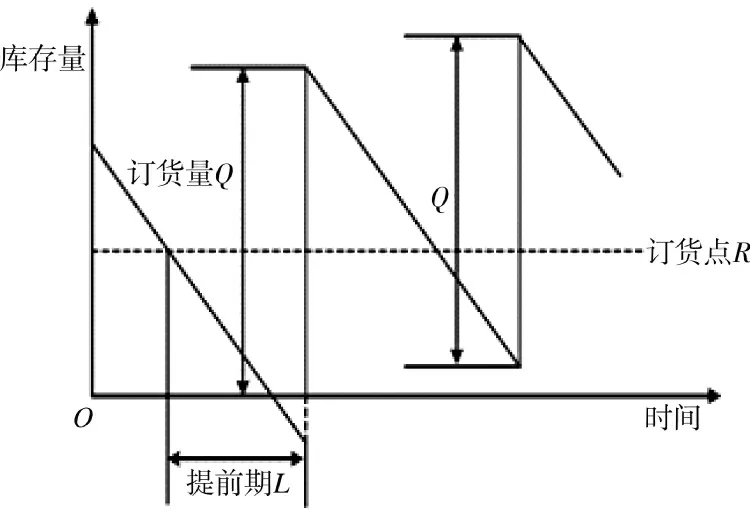
图5 （Q，R）库存控制策略

二类器材有左后制动器总成、右后制动器总成、主减速器壳、制动盘、制动器总成（左）、制动器总成（右）、双列圆锥滚子轴承、左转向节、右转向节、主动齿轮内轴承。此类器材具有库存量小、单价低、出货量低、缺货成本相对较小、需求波动和采购难度适中等特点，采用（t，S）周期型库存控制方法做好管理。对库存储备量进行间断型检查，检查周期为t，根据检查结果决定是否需要订货，检查时库存＜S 时，订购量为（S-当前库存），如库存＞S，则无需订货，等到下一个检查期继续检查并判断，如图6所示。

图6 （t，S）库存控制策略

三类器材有从动齿轮、制动鼓、主减速器主动齿轮、左制动钳总成、右制动钳总成。此类器材具有平均库存量低、消耗量低、缺货成本高、采购难度大、需求波动低、在装量小等特点，一般为周转件、偶换件，故障率低、订货难，器材的高可靠性导致了低需求，多个月的需求可能为零。然而，一旦发生短缺，损失是极其严重的。由于此类器材种类较少，历史数据较少，难以预测，可以根据（S-1，S）连续型库存控制策略进行订货（当消耗一个单位的器材，就发出订货申请，申请一个单位的器材，适用于消耗量较低的器材）或根据车辆装备检修实际情况进行订货。

四类器材有前桥壳焊接总成、后桥壳焊接总成。此类器材具有单价低、平均库存量低、占用资金高、消耗量低、供货量高等特点。可根据实际需要进行订货即可即时满足实际需求，无需采取上述库存策略。

6 结论

器材采购优先级分类的科学性、合理性直接影响装备维修的保障效益以及装备维修管理工作的有效性。本文研究了基于主成分聚类的多指标分类方法，解决了器材采购优先级多项因素、多级指标难以评价划分的问题。对聚类指标进行了选取，使用PCA 完成了指标降维；考虑器材采购优先级制定的实际情况，提出基于小样本的改进聚类算法，综合考虑聚类与主成分分析的分析结果，划分器材采购优先级别；用实例验证方法的可行性。结果表明，改进的k-means 分级情况较理想，分类的制定较为合理，有一定的可行性。但本文提出的方法还存在几点不足：一是由于涉及数据较为敏感，聚类时选用的指标变量较少，导致聚类结果较为单一；二是对器材采购优先级的分析过于理想，受各种因素影响，实际测算结果不一定可靠。以上不足将在下一步研究中做好完善。