浅析科学思维在数学模型建构过程中的培养路径
摘要 阐述了教师在构建数学模型过程中,应帮助学生正确地认识生物世界、增强学生进行科学思维的意识;在检验数学模型过程中,理解生物世界、诱导学生科学思维的发生;在完善数学模型过程中,充分解释生物世界、培养学生科学思维的形成;在应用数学模型过程中,科学地解决生物学问题、促进学生科学思维的发展。
关键词 高中生物学 科学思维 数学模型 建构过程 培养路径
中图分类号G633. 91
文献标志码 B
数学模型构建是在尊重生物学事实和逻辑证据的前提下,正确精准地反映客观事物本质及其规律的方法,是科学思维培养的有效载体。教师要遵从一定的逻辑规则,创造一切可以利用的机会,引导学生本着求真务实的求知态度,运用归纳与概括、演绎与推理、模型与建模、批判性思维等方法探讨生命现象及规律,正确应用逻辑思维规律进行推理活动并不断得到正确的结果,进而使学生能够审视或论证生物学社会议题。
1 在构建数学模型过程中增强学生科学思维的意识
构建数学模型的目的在于发现和揭示生物学现象、规律及规律背后的本质和意义,并借助模型解决一个或一类问题,因此,模型往往需要不断地完善修正,以普适于相似问题情境,解决类似问题。科学思维在具体→抽象→再具体→再抽象→……再具体中,实现了知识和能力螺旋循环上升的过程。
例如,在学习“种群数量变化规律”时,学生通过感受鲜活的生命现象,掌握了建立数学模型一般步骤(提出问题→作出假设→实验数据→数学表达→检验或修正),引发了建模兴趣。教师引导学生利用类比推理的方法继续探究:①学生通过起始个数为1的二分裂细菌,建立“Nt=2n(n代表分裂的次数)”的数学模型公式。②教师通过将细菌起点个数由实验中的“1”推广到了任何初始数量N0个(N0≥1),引导学生对模型进行第一次修正。学生经过提示、讨论后很快得到:Nt=No.2n。③教师提出将细菌种群的增长率设定为100%,学生进行第二次修正,得出“Nt=N0.(1+100%)n’。教师通过对原有公式中“2”的解读和分解,加深了学生对原有模型的理解,为下一步模型转换打下基础。④在第三次修正中,学生寻找种群的增长率,并设定为常数a,得出“N=N0.(1+a)n’。转换后的公式,大大拓宽了模型适用的范围。⑤教师讲授:种群增长率a=出生率一死亡率。当气候适宜、食物和空间条件充裕、没有敌害等完全理想条件下,种群的增长不会受种群密度增加等条件的影响,。值不变。此时,Nt=No.(1+。)”是指数函数。教师引导学生从细菌的实验室培养条件,到澳大利亚野兔、美国岛屿上环颈雉的种群数量快速增长的条件进行分析,建立种群增长模型的“J”型曲线,实现数学模型的转换,从而让学生完善了该模型的适用条件。⑥教师介绍:气候、食物、天敌、传染病以及受人工控制的种群数量不断增加,野生动植物种群数量不断减少等条件下,出生率和死亡率在不断地变化,种群的增长受种群密度增加的影响,种群增长率。也在不断地变化。学生讨论进行第四次模型修正:当a>0,a虽然在不断变小,但种群数量依然上升;当a=0,种群数量不变达到K值,种群数量处于稳定状态,种群建立曲线模型就是“S”型曲线;a<0,意味着种群出生率<死亡率,种群数量下降。教师引导学生综合分析,可以拓展出种群數量变化的类型有增长、稳定、波动、下降等发展变化规律。教师引导学生由最初的细菌模型推广到适合更多的生物种群,可为后续学习群落的结构、生态系统及其稳定性、生态环境的保护打下基础。最后,教师引导学生进行探究实验“培养液中酵母菌种群数量的变化”,讨论分析实验的结果与假设是否一致,帮助学生理解:推测的模型还需实验的验证,感悟建模价值。
在教学中,教师引导学生从具体的生物现象寻找规律后建立抽象的数学模型.又用抽象的数学模型来解释具体的生物学现象与规律。学生用数学语言解释种群数量增长的规律,始终围绕“数学模型构建的程序”这一主线,对数学公式不断地修正及模型的转换,加深对数学模型的理解,体悟建立模型的科学研究方法,发展尊重实验结果、事实求是的严谨态度,认同人类活动对生物种群数量变化的重要影响。教学过程真正体现了建构性、生成性、多元性的高度统一。
2 在检验数学模型过程中诱导学生科学思维的发生
检验数学模型就是引导学生运用数学的方法去思考问题、用数学的语言去解决问题。在解决问题的过程中,学生需要对数学模型的有效性进行合理评估,包括确认所建模型和研究对象之间一致性以及验证模型在问题解决中的可用性两部分内容。教师进行有效性评估时,要始终注重数学思维的逻辑。
细胞有氧呼吸反应式(以葡萄糖为呼吸底物)中,C6H12O6、O2、CO2三者间物质的量比例关系为1:6:6。该比例关系形象直观,反映了物质变化的本质,简化了有氧呼吸过程中物质变化的数学关系,提高了课堂教学的效率。教师引导学生验证该数学模型,能够激发学生的科学思维。从定性的角度,教师可以通过人教版教材《必修1.分子与细胞》中的“探究酵母菌细胞呼吸的方式”的实验,配合显色反应,证明有CO2产生;用真空袋分别装加发酵粉的面团(留有空气)和没加发酵粉的面团(不留空气),证明有氧呼吸过程中水的生成,进而让学生尝试建构酵母菌细胞有氧呼吸中物质变化的方程式。从定量的角度,教师可以采用2020版苏教版教材《必修1.分子与细胞》中“探究酵母菌细胞呼吸的方式”实验所建议的注射器进行定量分析。由于注射器的气密性和活塞的摩擦力等影响因素,实验结果必然存在误差。教师可引导学生运用计算机数据采集系统自动迅速地采集并记录锥形瓶溶液中溶解氧、空间中的CO2和O2浓度数值,并应用Excel软件和Origin软件作溶解氧、CO2和O2浓度的变化曲线,从而准确分析在有氧呼吸过程中O2消耗量与CO2产生量之间的关系,帮助学生领会有氧呼吸的变化实质。在学生建模成功后,教师引导学生运用模型解决问题。
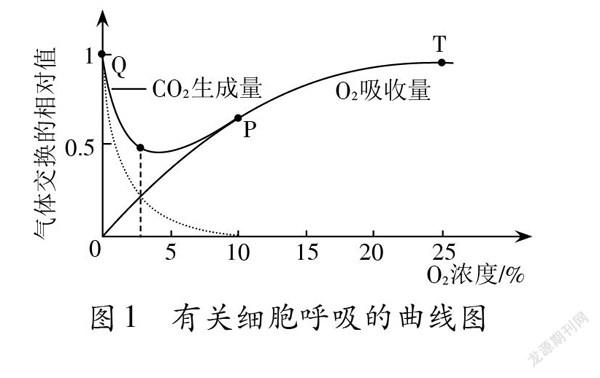
(1)细胞呼吸类型的判断。在以葡萄糖为呼吸反应物的情况下,通常分析02的消耗量和C02的生成量(以产生酒精的无氧呼吸为例)来判断呼吸的类型。依据有氧呼吸与无氧呼吸反应过程中葡糖糖、氧气和二氧化碳的系数关系,可进行判断。①当有氧呼吸与无氧呼吸反应速率相等时,则共需吸收6分子氧气,生成8分子二氧化碳,即CO2的生成量与O2的消耗量的比值为4:3。②当CO2的生成量与O2的消耗量的比值为4:3,则有氧呼吸速率等于无氧呼吸速率。③当CO2的生成量与O2的消耗量比值大于4:3,则无氧呼吸与有氧呼吸共同进行,且无氧呼吸占主体地位。④当CO2的生成量与O2的消耗量比值小于4:3,则无氧呼吸与有氧呼吸共同进行,且有氧呼吸占主体地位。
(2)分析曲线(图1)中细胞呼吸的方式(以葡萄糖为呼吸底物)。①Q点代表不消耗O2,产生CO2,只进行无氧呼吸;②P点及P点以后,消耗O2量等于产生CO2量,细胞只进行有氧呼吸过程;③QP段,产生CO2量大于消耗O2量,同时进行有氧呼吸和无氧呼吸。
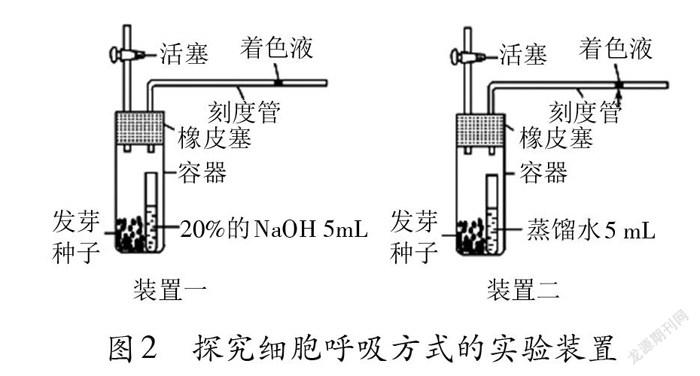
(3)设计实验探究细胞呼吸的方式。①实验设计:为确认某生物的呼吸类型,应设置两套呼吸装置,如图2所示(以发芽种子为例);②实验结果预测和做出结论。若装置一液滴不移动,装置二液滴不移动,说明种子只进行产乳酸的无氧呼吸或种子己死亡;若装置一液滴不移动,装置二液滴右移,说明种子只进行产生酒精和CO2的无氧呼吸;若装置一液滴左移,装置二液滴右移,说明种子进行有氧呼吸和产生酒精的无氧呼吸;若装置一液滴左移,装置二液滴不移动,说明种子只进行有氧呼吸或进行有氧呼吸和产乳酸的无氧呼吸。
3 在完善数学模型过程中培养学生科学思维的形成
教师引导学生基于同一个问题的模型,不断地修饰和延伸,拓展出不同的模型,并应用到不同的实际问题中,从而对事物本身属性背后的逻辑关系进行多角度、多层次的分析。
自由组合定律的“9:3:3:1”变式就是对原有数学模型进行不断修饰、完善的过程,多对基因之间除了相互独立遗传之外,还有以下几种情况:①如果只有在两对非等位显性基因同时存在时才能决定某一表型,则称两对基因存在基因互补作用(效应)。即两显性基因同时出现才为一种表型,其余的基因型中任意一对基因或两对基因发生隐性纯合均无法表现出这一表型。此时,自由组合的子代比率修饰为9(A—B一):7(3A_bb+3aaB_+laabb),即9:7,测交后代比例为1:3。②两对非等位基因作用相同,且表现型能够叠加出现双显、单显、双隐三种表现型的基因累加作用(效应)。此时,自由组合的子代比率修饰为9(A—B一):6(3A_bb+ 3aaB_):laabb,即9:6:1,测交后代比例1:2:1。或者是当A与B的作用效果相同,但显性基因越多,其效果越强时,两对基因存在基因累加作用(效应)。模型为1(AABB):4(AaBB+AABb):6(AaBb+AAbb+ aaBB): 4(Aabb+ aaBb):1(aabb),即1:4:6:4:1,测交后代比例1:2:1。③一对基因在隐性状态下可抑制或掩盖另一对非等位基因的表达,存在aa(或bb)时表现为一种表型的隐性上位作用(效应),其余正常表现。此时,自由组合的子代比率修饰为9A_B_:3A_bb:4(3aaB_+laabb)或9A_B_:3aaB_:4( 3A_bb+laabb),即9:3:4,测交后代比例1:1:2。④一对基因在显性状态下(显性纯合或杂合)可抑制或遮盖另一对非等位基因表达的显性基因上位作用(效应),只有当显性上位基因不存在时,下位基因才表达。此时,自由组合的子代比率为12(9A_B_+3A_bb):3aaB_: laabb,即12:3:1,测交后代比例2:1:1。⑤由于一对等位基因表现显性时(杂合或显性纯合),能抑制另一对基因表达的基因抑制作用(效应),所以双显性、双隐性和一种单显性表现为一种表型,另一种单显性表现为另一种表型。此时,子代比率修饰为13(9A_B一+3aaB一+laabb):3A_bb或13(9A_B_+3A_bb+laabb):3aaB_,即13:3,测交后代比例3:1。⑥两对非等位基因对表现型产生相同的影响,只要具有显性基因其表型就一致,其余基因型为另一种表型,表现为基因重叠作用(效应)。此时,自由组合的子代比率修饰为15(9A_B_+3A_bb+3aaB_):laabb,即15:1,测交后代比例3:1。⑦如果子代中各表型所占份数之和小于16,则可能存在致死情况。由组合的子代比率修饰为4:2:2:1,表示的是AA、BB均可以使个体死亡,即2AaBB、2AABb、1AABB、lAAbb、laaBB均死亡;孟德尔比率修饰为6:3:2:1表示的是BB(或AA)使个体死亡,即2AaBB、IAABB、laaBB(或2AABb、IAABB、lAAbb)死亡。⑧不同对的两个基因相互作用,出现了新的表型,但孟德尔比率仍然为9:3:3:1,表现为基因互作作用(效应)。⑨10:3:3、10:6、12:4等数学模型在目前科学研究中还未发现。
在強化体悟遗传规律数学模型完善的实践活动中,教师利用有效的问题,引导学生主动开展论证型科学思维活动。在这种不断修饰、完善、延伸和拓展中全面优化学生的科学思维结构,逐步培养学生的生物学学科核心素养,最终全面提升学生利用科学思维来认识事物、解决问题的意识能力。
4 在应用数学模型过程中提高学生科学思维的发展
建构模型时,需要将构建好的数学模型应用到真实的学习情景中,用不同的科学思维方法循环往复地重新思考,提出新的假设,建立新的数学模型,直到预期结果与实际结果相符为止。教师要引导学生用一个己知的结论去推导一个新的结论,合理地完善和弥补原有模型存在的不足,将科学思维内化为能力,从而能解释或预测某些生物学现象,创造性地解决一个或一类复杂多变的问题,从而提升思维的严密性。
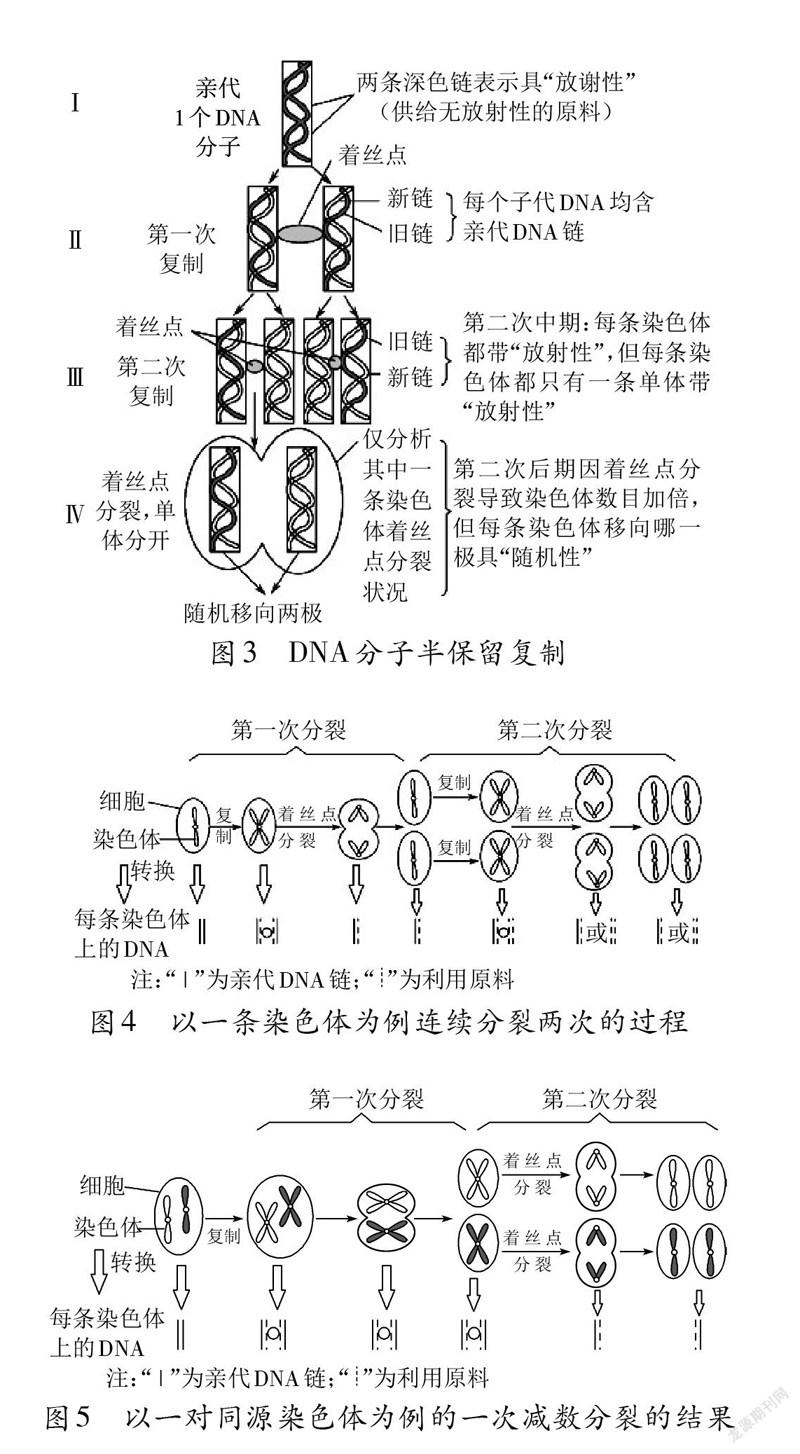
DNA分子复制的特点之一是半保留复制。1个两条链都被32p标记的DNA分子放在含3ip的培养基上培养。(1)若子代DNA分子数为28个,无论复制多少次,含32p的DNA分子始终是2个;含3ip的DNA分子有2“个,只含3ip的DNA分子有(28—2)个。(2)当子代DNA分子总链数为2“x2= 2n+l条时,复制n(n≥1)次,含32p的链永远是2条;含3ip的链数是(2n+1—2)条。这个数学模型通常被用于解决细胞分裂过程中的同位素标记问题:①首先是结合染色体复制,解读DNA分子半保留复制的图像(图3);②分析有丝分裂中核DNA和染色体的标记情况,有丝分裂过程中核DNA复制一次细胞也分裂一次。如图4所示是以一条染色体为例连续分裂两次的过程。由图可知,第一次有丝分裂形成的2个子细胞中所有核DNA分子均由一条亲代DNA链和一条子链组成,以体细胞染色体数为2n为例,第二次有丝分裂后最终形成的子细胞中含亲代DNA链的染色体条数是0-2n。③分析减数分裂中核DNA和染色体的标记情况,在减数分裂的过程中,DNA复制一次细胞连续分裂两次。如图5所示是以一对同源染色体为例的一次减数分裂的结果。由图可知,减数分裂过程中细胞虽然连续分裂两次,但DNA只复制一次,所以4个子细胞中所有核DNA分子均由一条亲代DNA链和一条利用原料合成的子链组成。最后,教师利用例题帮助学生巩固模型建构的成果。学生在运用数学模型、渗透模型思维解答习题过程中,体验了从不同的角度和不同的维度去观察、分析和思考生物学问题,把抽象问题具体化、解题过程规律化,进而有效地主动建构生物学知识,把握生物学科的迁移规律,推动和发展了认知水平,逐步推动科学思维的高阶发展,发展创新型思维和创造性能力。
数学模型建构与生物学教育内容的相互渗透、多层次启发。教师要建立并完善模型的过程,以促进生物学课堂焕发出生命活力,同时促进了学生学习方式改进和革新,有助于学生灵活运用合适的技能或手段解决现实问题,使学生终身需要的科学思维得以健康发展,推动实施立德树人的素质教育。
参考文献:
[1]秦亚平.高中生物学教学中理性思维的缺失及其对策[J].生物学教学,2012,22(1):21-23.
[2]吴海峰.浅谈“探究学习”在“种群数量变化规律”一节中的应用[J].中学生物教学,2012,(9):41-43.
[3]吴海峰.促进“深度学习”的教学实践与思考——以“探究酵母菌细胞呼吸的方式”实验教学内容为例[J].中学生物学,2021,37(1):44-46.
[4]李华.两对等位基因控制一对相对性状遗传的分析[J].生物学教学,2010,35(3): 58-60.
[5]吴春萍,金莉.关于“细胞分裂中染色体与DNA的放射性追踪”试题特点及难点突破[J].生物学通报,2020,55(4):49-51.
[6] 中华人民共和国教育部.普通高中生物学课程标准(2017年版2020年修订)[S].北京:人民教育出版社,2020.

