例说物理论证题的隐性表达与显性表达

广西桂林市国龙外国语学校（541004） 唐昌琳

语言表达分为显性表达与隐性表达。显性表达意境显现，一语中的，让读者不用揣摩就能理解表达者的真实意图。隐性表达则反之，文字含蓄，意境模糊，有的甚至不完整，需要读者根据前后文进行揣摩、感悟、推理才能正确理解表达者的真实意图。

高中物理有一种题型叫论证题，在解答论证题时读题审题、过程分析、推理论证等都可在大脑中完成，但最后解题过程的呈现还是需要进行书面表达。怎样表达才能更加科学，更加通俗易懂，使读者一看便知，是值得教师深入思考的。下面摘录三个学生作业中的隐性表达与显性表达案例，并进行对比说明，与大家分享。

一、实验题中的论证题型

［案例1］（2021 年高考全国甲卷第23 题）某同学用图1 所示电路探究小灯泡的伏安特性，所用器材有：小灯泡（额定电压2.5 V，额定电流0.3 A）、电压表（量程300 mV，内阻300 Ω）、电流表（量程300 mA，内阻0.27 Ω）、定值电阻R0、滑动变阻器R1（阻值0～20 Ω）、电阻箱R（2最大阻值9 999.9 Ω）、电源E（电动势6 V，内阻不计）、开关S、导线若干。完成下列填空：

图1

（1）有3个阻值分别为10 Ω、20 Ω、30 Ω的定值电阻可供选择，为了描绘小灯泡电流在0～300 mA的U-I曲线，R0应选取阻值为_____Ω的定值电阻；

（2）闭合开关前，滑动变阻器R1的滑片应置于变阻器的_______（填“a”或“b”）端；

（3）在流过电流表的电流较小时，将电阻箱R2的阻值置零，改变滑动变阻器滑片的位置，读取电压表和电流表的示数U、I，结果如图2 所示。当流过电流表的电流为10 mA 时，小灯泡的电阻为______Ω（保留1位有效数字）；

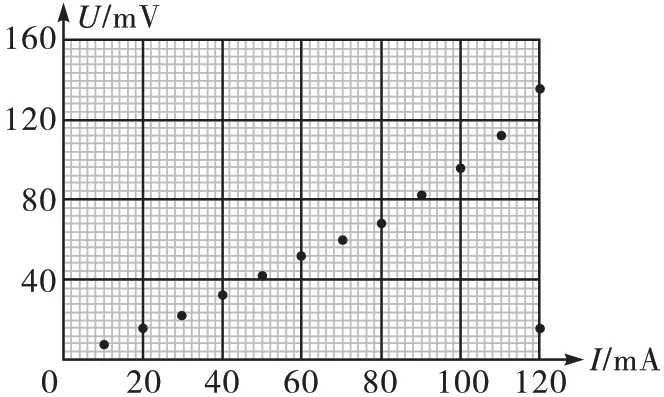
图2

（4）为使电压表满量程时对应于小灯泡两端的电压为3 V，该同学经计算知，应将R2的阻值调整为______Ω。然后调节滑动变阻器R1，测得数据如下表所示：

（5）由图2 和上表可知，随流过小灯泡电流的增加，其灯丝的电阻_________（填“增大”“减小”或“不变”）；

（6）该同学观测到小灯泡刚开始发光时流过电流表的电流为160 mA，可得此时小灯泡电功率P1=_______W（保留2位有效数字）；当流过电流表的电流为300 mA 时，小灯泡的电功率为P2，则__________（保留至整数）。

在考试中，实验题最后呈现的是一个答案，解题过程不能呈现出来。笔者把这道实验题布置给学生，让学生独立完成，要求在题后附上翔实的解答过程，结果在第（1）、（5）问的解答中出现了隐性表达、显性表达与错误表达三种情况。

解答第（1）问时的隐性表达：小灯泡在额定条件下工作时的电阻为因该电阻比较小，所以选作保护电阻的R0应选阻值小的，即选10 Ω 的定值电阻。答案是对了，但逻辑表达不清楚。小灯泡的额定工作电阻较小，保护电阻就选小的，这只是猜测，是站不住脚的。根据题给电源电动势为6 V 的条件，要保证小灯泡安全并能达到额定工作条件，细细推敲一下，在本题中学生的猜测又是正确的。这种需要揣摩的表达是典型的隐性表达。

解答第（1）问时的显性表达：在移动滑动变阻器的滑动臂时，若误将滑动臂移至b端，要保证小灯泡的安全，保护电阻R0与电流表应分担电压：U1=E-U0=3.5 V，根据欧姆定律可知rA≅11.4 Ω，比10 Ω 大。若选用R0=20 Ω 的定值电阻，假设小灯泡能在额定条件下工作，此时小灯泡的电阻为，小灯泡分得的电压为，这样小灯泡达不到额定工作电压。综合考虑，R0应选10 Ω 的定值电阻。只是在移动滑动变阻器的滑动臂时动作要慢，注意观察，不要让小灯泡两端的电压超过2.5 V。这种论证，理由充分，逻辑清晰，读者一看便清楚了，属于显性表达。

解答第（5）问时的错误表达：把图2 中各点用平滑曲线连接起来，曲线的斜率明显越来越大，所以随流过小灯泡电流的增加，其灯丝的电阻增大。这个答案是正确的，但论证是错误的，在U-I曲线中斜率不代表电阻阻值。根据欧姆定律，电阻的阻值应满足事实上用第（4）问表格中前、中、后3 组数据代入可以发现随着流过小灯泡电流的增加，其灯丝的电阻增大。原因是一般金属材料的电阻率随温度的增大而增大，满足ρ=ρ0(1+αt)，α为大于0 的温度系数，t为温度。当流过小灯泡的电流增大时，灯丝功率增大，温度升高，灯丝的电阻率增大。

二、计算题中的论证题型

［案例2］（2021 年全国高考广东卷第13 题）算盘是我国古老的计算工具，中心带孔的相同算珠可在算盘的固定导杆上滑动，使用前算珠需要归零，如图3 所示。水平放置的算盘中有甲、乙两颗算珠未在归零位置，甲靠边框b，甲、乙相隔s1=3.5×10-2m，乙与边框a相隔s2=2.0×10-2m，算珠与导杆间的动摩擦因数μ=0.1。现用手指将甲以0.4 m/s 的初速度拨出，甲、乙碰撞后甲的速度大小为0.1 m/s，方向不变，碰撞时间极短且不计，重力加速度g取10 m/s2。

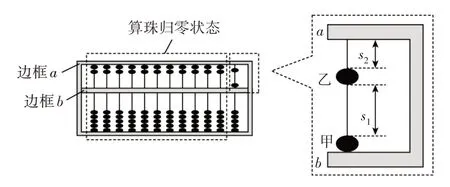
图3

（1）通过计算，判断乙算珠能否滑动到边框a；

（2）求甲算珠从拨出到停下所需的时间。

解答1（隐性表达）：（1）甲拨出速度为v0，与乙碰前速度为v1，由动能定理有：

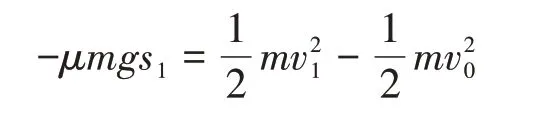
解得：v1=0.3 m/s

甲、乙碰后的速度分别为v2、v3，由动量守恒有mv1=mv2+mv3，解得v3=0.2 m/s。

乙运动到边框a需克服摩擦力做功W=μmgs2=0.02m（J）。

因为EK=W，所以乙算珠能滑动到边框a。

（2）甲从拨出到与乙碰前需时t1，由动量定理有-μmgt1=mv1-mv0，解得t1=0.1 s。

碰后甲的速度v2＜v3，说明甲不能滑到边框a，碰后到甲停下需时t2，则由动量定理有：

-μmgt2=0-mv2，解得t2=0.1 s。

甲算珠从拨出到停下所需时间t=t1+t2=0.2 s。

解答2（显性表达）：（1）甲拨出速度为v0，与乙碰前速度为v1，则由动能定理有：

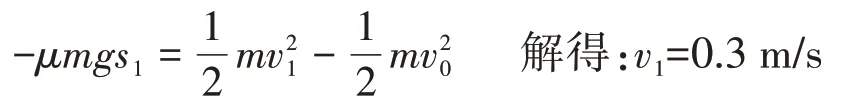
甲、乙碰后的速度分别为v2、v3，由动量守恒有mv1=mv2+mv3，解得v3=0.2 m/s。

碰后乙能运动的距离为s，由动能定理有-μmgs解得s=0.02 m。

因为s=s2，所以乙恰能运动到边框a。

（2）甲从拨出到与乙碰前需时t1，则由动量定理有-μmgt1=mv1-mv0，解得t1=0.1 s。

碰后甲的速度v2＜v3，说明甲不能滑到边框a，碰后到甲停下需时t2，则由动量定理有：

-μmgt2=0-mv2，解得t2=0.1 s。

甲算珠从拨出到停下所需时间t=t1+t2=0.2 s。

本题的解答方法很多，以上摘录的是用动能定理、动量定理解题的两种表达。解答1 的表达就是一种隐性表达，距离是显性的，能量是隐性的。碰后乙具有0.02m（J）的动能，要运动到边框a需要克服摩擦力做的功恰为0.02m（J），可以证明乙算珠能到达边框a。但这个证明需要转换思维才能理解，不直观；题目已经给定乙算珠距离边框a0.02 m，甲、乙碰后，如果乙能运动0.02 m（含）以上，就能到达边框a。计算出碰后乙能运动的距离，再判断乙能不能到达边框a就一目了然了，所以解答2 的表达很直观，是显性表达，让读者一看就知道了。对比后，显性表达的优势是明显的。

［案例3］（桂林市统考题）如图4 所示，在水平轨道右侧固定半径为R=0.4 m 的竖直圆形光滑轨道，水平轨道的PQ段铺设有特殊材料，长度为L=1.0 m，水平轨道左侧有一轻质弹簧，左端固定，弹簧处于自然伸长状态。可视为质点的小物块从轨道右侧A点以初速度v0=6 m/s 冲上轨道，依次通过圆形轨道、水平轨道后压缩弹簧，并被弹簧以原速率弹回。已知物块质量m=1 kg，与PQ段间的动摩擦因数μ=0.2，轨道其他部分摩擦不计，重力加速度g=10 m/s2。求：

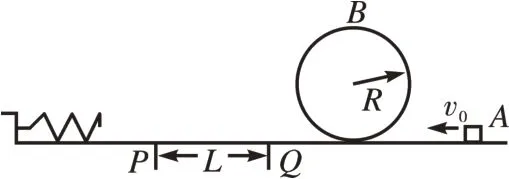
图4

（1）物块经过圆形轨道最高点B时对轨道的压力大小；

（2）弹簧获得的最大弹性势能；

（3）请分析物块被弹簧以原速率弹回后，能否不脱离圆形轨道返回A点继续向右运动。

解答1（隐性表达）：（1）物块上升到圆形轨道最高点B的速度为vB，由动能定理有：

在B点物块的受力情况如图5 所示，轨道对物块向下的压力为FN，由牛顿第二定律有：

图5

FN+mg=解得FN=40 N。

（2）克服弹簧弹力做的功全部转化成弹性势能，设最大弹性势能为Epm，从A到弹簧压缩至最短，由功能原理有解得Epm=16 J。

（3）从弹簧压缩最短到物块向右回到圆形轨道最低点的动能为EK，由功能原理有：

Epm-μmgL=EK，

解得EK=14 J。

物块通过B点时的受力情况如图5 所示，重力为恒力，过B点的速度越大，轨道对物块的压力FN越大。过B点的速度越小，轨道对物块的压力FN越小，当压力FN为0 时，由重力提供物块做圆周运动所需的向心力，对应物块刚好能做完整圆周运动过B点的最小速度。因此，物块过B点的最小速度v1满足解得v1=2 m/s。

物块过B点的最小机械能10 J。

因为EK＞E，所以物块能通过B点不脱离轨道，返回A点继续向右运动。

解答2（显性表达）：（1）设物块上升到圆形轨道最高点B的速度为vB，由功能原理有：

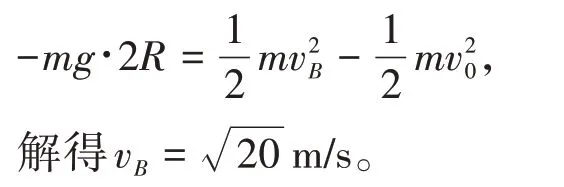
在B点，轨道对物块向下的压力为FN，由牛顿第二定律有：

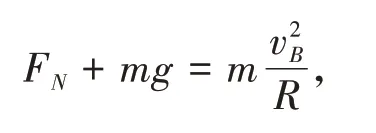
解得FN=40 N。

根据牛顿第三定律可知，物块经过圆形轨道最高点B时对轨道的压力大小FN′=FN=40 N。

（2）克服弹簧弹力做的功全部转化成弹性势能，设最大弹性势能为Epm，从A到弹簧压缩至最短，由功能原理有：

解得Epm=16 J。

（3）物块要过B点的最小速度为v1，由牛顿第二定律有：

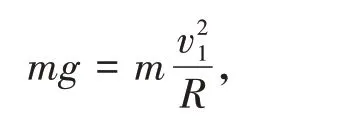
解得v1=2 m/s。

假设物块能不脱离轨道返回到B点的速度为v2，从弹簧压缩最短到物块向右回到圆形轨道B点，由功能原理有：

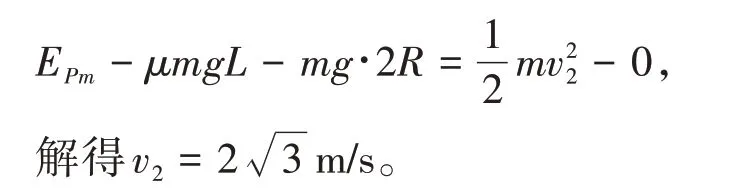
因为v2＞v1，所以假设成立，物块能通过B点不脱离轨道，返回A点继续向右运动。

解答1 的表达中有两处属于隐性表达。第一处是（1）中求物块在B点时对轨道的压力。物块对轨道的压力不能以轨道为研究对象直接求出，只能以物块为研究对象，求出轨道对物块的压力。物块对轨道的压力跟轨道对物块的压力是一对相互作用力，这是牛顿第三定律。解答1 中只求出了轨道对物块的压力，要读者根据牛顿第三定律推理才知道物块对轨道的压力，这既属于隐性表达，也属于问题未完全解决，在考试评分时会相应扣分；第二处是（3）中，要证明物块被弹簧以原速率弹回后，能否不脱离圆形轨道返回A点继续向右运动，则必须证明物块返回后，能否通过圆形轨道最高点B。物块在竖直圆形轨道上的运动属于无支撑类型，物块要在竖直平面内做完整圆周运动而不脱离轨道，则在过最高点B时有最小速度，这是一个大家都熟知的二级结论，只有物块在最高点的速度v≥vmin才不会脱离轨道。厘清这一关系后，只要求出物块在竖直平面内在圆形轨道上做完整圆周运动通过最高点B的最小速度vmin，再求出物块返回B点时的实际速度v，比较v≥vmin是否成立，就可判断物块能否不脱离圆形轨道返回A点继续向右运动了，解答2 就是利用这个二级结论进行解答的，属于显性表达。在解答1 的表达中，求出物块返回圆形轨道最低点时具有的动能为14 J，再求出物块要过最高点B必须具有的最小机械能为10 J，考虑到在最低点的动能大于要过最高点的最小机械能，所以物块能不脱离轨道返回A点继续向右运动。这一证明思路是没错的，但不是人们常用的判断在竖直面内做无支撑圆周运动条件的直接证据，不直观，需要读者揣摩才能理解，属于隐性表达。当然其中也有不规范的地方，按这一思路证明，需证明物块在圆形轨道最低点的机械能大于过最高点所需的最小机械能。首先要规定零势面，如果以水平轨道所在平面为零势面，物块在圆形轨道最低点的机械能为14 J，过最高点所需最小机械能为10 J，这样才规范。

通过以上三个案例的分析，在解答物理论证题时，用大家所熟知的、直观的显性表达，更容易被大家所接受。